Introducción
Siguiendo una estructura análoga a la anterior, procederemos a desarrollar la ecuación que describe la característica central del modelo de interés compuesto: la capacidad de generar intereses adicionales. Además, sentaremos las bases para abordar la aplicación de tasas de interés y establecer relaciones entre ellas, con el propósito de calcular tasas equivalentes.
El interés compuesto representa la segunda modalidad de pago de intereses. Su rasgo distintivo es la generación de nuevos intereses a medida que transcurre el tiempo o cada período específico. Estos intereses recién generados se suman al capital original, que luego comienza a generar intereses por sí mismo, repitiendo este proceso según lo establecido. Similar al modelo de interés simple, los intervalos de tiempo pueden ser mensuales, anuales, trimestrales, semanales, entre otros.
Interés compuesto
El modelo de interés compuesto es ampliamente empleado en contratos comerciales y operaciones financieras en todo el mundo, e incluso está respaldado por la legislación vigente en nuestro país, como lo establece la Ley Federal de Protección al Consumidor.
Para comenzar con su construcción, se propone el siguiente ejemplo:
A una persona les prestan \$100, con una tasa de interés efectiva mensual del 10%, dicho monto al término del primer mes estaría generando \$10 por concepto de interés más los \$100 pesos originales. La parte interesante comienza a ocurrir a partir del segundo mes, en el que los intereses que ya se habían generado durante el primer mes comienzan a generar nuevos intereses invertidos a la misma tasa, esto es:
Monto del periodo anterior $=\$110$
Intereses del segundo periodo $=(\$110)(0.10)=\$11$
Lo que nos da un monto total al final del segundo periodo de \$121. Es importante hacer mención que el $1 que aparece en nuestro último resultado, representa los intereses generados por los nuevos intereses. En la siguiente gráfica se representa con detalle este proceso.
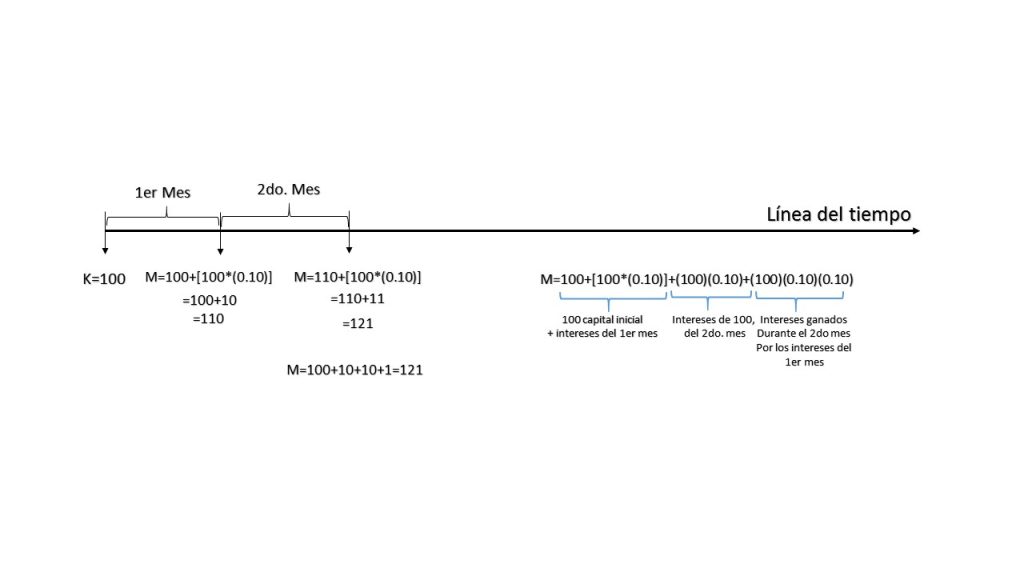
Ahora bien, se va a construir el modelo general de Interés compuesto:

El primer periodo comienza con un capital $K$, con una tasa de interés $i$, de tal manera que al final del primer periodo tenemos el capital inicial más los intereses generados durante ése periodo, y nos quedaría una expresión como la siguiente: $M=K+Ki$.
Por consiguiente, el monto del segundo periodo queda como el capital inicial más los intereses obtenidos en el 1er y 2do periodo.
Es importante recalcar que los intereses se calculan multiplicando el capital por la tasa de interés. Si los intereses generados en el 1er periodo fueron $Ki$, entonces los intereses generados en el segundo periodo se calcularon a partir de la expresión $Kii$. De esta forma, el monto obtenido al final del segundo periodo se representa con la expresión: $M=K+Ki+Ki+Kii$, la cual se reduce a la expresión señalada en la figura 1.5> $M=K(1+i)^2$.
Generalizando la fórmula queda lo siguiente: $M=K(1+i)^t$. En ésta expresión la variable $t$, es la que va a estar representando el número de periodos, el cual va a estar ligados siempre con el «apellido» de la tasa de interés, este es mensual, semanal, diario, etc. como ya en algunos párrafos anteriores se ha hecho mención.
Las reglas para aplicar correctamente este modelo son semejantes a la del modelo de interés simple, con algunas variantes, pero para no dejar ambigüedad alguna se enuncian a continuación:
- El valor de las variables $K$ y $M$ se escriben en unidades monetarias, siendo la primera que representa el capital inicial ($K$), mientras que la segunda representa el monto ($M$).
- $i$ es la tasa de interés efectiva por periodo, expresada en %, y al realizar cálculos usada al tanto por uno, es decir ya dividida entre 100.
- La periodicidad de la tasa determina la unidad de tiempo con la que se va a utilizar la variable $t$, esto es, en años, meses, bimestres, durante el lapso de tiempo acordado que dure la operación.
Siguiendo una lógica similar al modelo de interés simple, en el caso del modelo de interés compuesto, tenemos la capacidad de expresar cualquier variable en función de las otras tres. Es decir, podemos despejar y expresar cualquier variable en términos de las demás.
Por lo anterior podemos establecer que, partiendo del modelo de interés compuesto, $K$ se puede calcular a partir de la siguiente expresión:
$$K=M\frac{1}{(1+i)^t}=M(1+i)^{-t}.$$
Para obtener $i$, se divide entre $K$ la ecuación de interés compuesto, luego se eleva a la potencia $\frac{1}{t}$ y por último se le resta uno, con lo que se llega a:
$$i=\frac{(M)}{(K)}^{\frac{1}{t}}-1.$$
Finalmente, para expresar $t$ es necesario usar algunas propiedades de los logaritmos, como se observa a continuación:
$$t=\frac{\log M-\log K}{\log(1+i)}.$$
Es fundamental destacar una diferencia significativa en comparación con el modelo de interés simple, que, como ya hemos visto, exhibe un comportamiento lineal. Por otro lado, el modelo de interés compuesto muestra un comportamiento geométrico, como se puede apreciar en el siguiente gráfico:
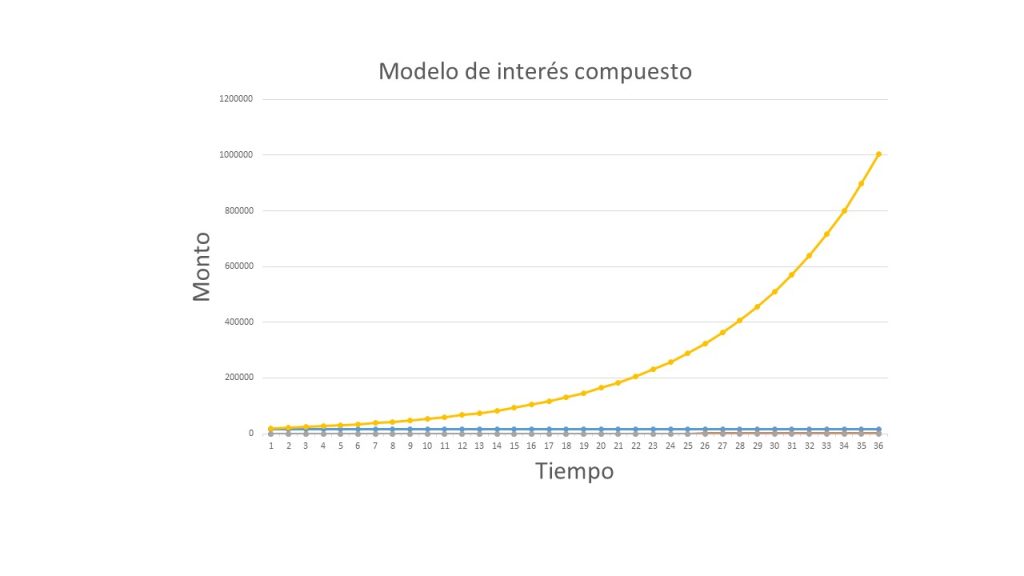
En la figura 1.6, se muestra un ejemplo de cómo se comporta el modelo de interés compuesto, bajo una inversión de un capital de \$1700 invertido durante 3 años, a una tasa mensual del $12\%$.
Relación interés simple con el interés compuesto
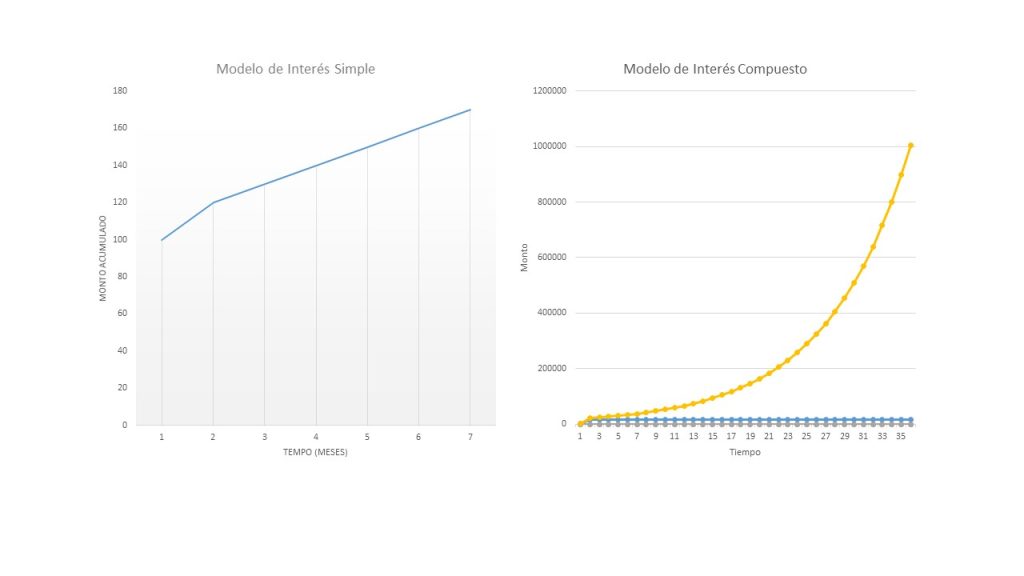
Su principal relación radica en como se calcula el crecimiento del dinero a través del tiempo, ya que ambos sirven para determinar cuanto se gana o se debe de pagar, pero se obtienen resultados distintos, mientras el interés simple los intereses solo se calculan sobre el monto inicial, es decir los intereses no se reinvierten; lo que genera un crecimiento lineal. Mientras que el interés compuesto se calculan intereses sobre intereses, en otras palabras los intereses se calculan no solo sobre el monto inicial, sino también sobre los intereses que se van generando mes con mes, los intereses se reinvierten, lo que genere un crecimiento con un comportamiento exponencial.
Cabe señalar que si el tiempo que dura la transacción es corto, el comportamiento de ambos es muy similar, pero a largo plazo es cuando la diferencia queda mas marcada ya que se genera mas dinero con el modelo de interés compuesto.
Ejercicios resueltos
Ejercicio. ¿Cuál es el monto que se genera, con un capital inicial de \$2500 y lo queremos invertir con las siguientes tasas de interés, durante los periodos que se indican:
- A una tasa del 6.5% anual, durante tres años y 6 meses.
- 2.4% mensual, luego de haber transcurrido dos años y 8 meses.
- 5.8% semestral, después de un periodo de 10 meses.
- 0.04% diario, después de un año con 23 días.
Solución
- El monto inicial ($K$), que se va a utilizar es el mismo, el cual es de \$2500, y de igual forma, en todos los casos queremos saber el monto ($M$). Una vez aclarado ese punto, el modelo que vamos a estar usando es el de interés compuesto dado por: $M=K(1+i)^t$.
Se sabe que la tasa es una tasa efectiva anual del 6.5%, motivo por el cual la variable $t$ será expresada en años, así mismo, el tiempo que se tiene considerado que dure la operación, es de 3 años con 6 meses. Ahora bien, sustituyendo cada uno de los valores en nuestra ecuación de interés compuesto:
\begin{align*}
M&=2500(1+0.065)^{3\frac{1}{2}}\\
&=2500(1+0.065)^{3.5}\\
&=3116.47
\end{align*}.
Es importante señalar, que el número 3 corresponde a los años completos que dura el acuerdo, mientras que el $\frac{1}{2}$, es por los 6 meses que hacen falta, el cual expresado en años sería un medio. De manera tal que $t=3\frac{1}{2}=3.5$. - Se tiene una tasa efectiva mensual ($i$) de 2.4%, lo cual implica que el tiempo ($t$) que asciende a 2 años 4 meses debe ser expresado en meses, entonces aplicando el modelo:
$$M=2500(1+0.024)^{28}=4856.67$$ - Análogamente, si la tasa es del 5.8% semestral, el tiempo debe ser expresado en semestres, motivo por el cual $t= 1 semestre + \frac{4}{6} semestre=1+\frac{4}{6}=1+\frac{2}{3}=\frac{5}{3}=1.67$, y aplicando el modelo se obtiene:
\begin{align*}
M&=2500(1+0.058)^{1\frac{4}{6}}\\
&=2500(1+0.058)^{1.67}\\
&=2746.31
\end{align*} - De forma parecida a los incisos anteriores, la tasa efectiva diaria 0.04% ($i$), esto causa que se mida en días la variable $t$, y se va a considerar que en un año se tiene 365 días, lo cual implica:
$t=365 +23 días=386 días$,
luego entonces nos da el siguiente resultado al aplicar el modelo de interés compuesto
$$M=2500(1+0.0004)^{365+23}=2500(1+0.0004)^{386}$$
Ejercicio. Calcula la tasa de interés anual, que se necesita calcular para los siguientes incisos:
- Monto inicial de \$1 500, durante un año genera un monto de \$1 800.
- Monto inicial de \$27 500, que durante un lapso de un año y cinco meses genera \$30500.
- Monto inicial de \$22 000, durante un lapso de 7 semestres con 5 meses, genera un monto total de \$25 000.
Solución
A partir del modelo de interés compuesto, con el que se ha estado trabajando, se sabe que contamos con el valor de las variables $K$, $M$ y $t$. Por lo anterior, se va a hacer uso de la siguiente expresión que anteriormente ya se había deducido:
$$i=\frac{(M)}{(K)}^{\frac{1}{t}}-1$$
- Sustituyendo cada uno de los valores de la expresión anterior, se tiene:
$i=(\frac{1800}{1500})^1-1=0.2$
lo cual implica que la tasa de interés es $i=20\%$ - Análogamente al ejercicio anterior, se tiene:
\begin{align*}
i&=\left(\frac{30500}{27500}\right)^{1+\frac{5}{12}}-1\\
&=\left(\frac{30500}{27500}\right)^{\frac{17}{12}}-1\\
&=\left(\frac{30500}{27500}\right)^{1.416}-1\\
&=0.15
\end{align*}
Por lo tanto, el valor de la tasa de interés es: $i=15\%$ - En este caso se debe observar que un año tiene 2 semestres, por lo que la cantidad de 7 semestres, tiene 3.5 años. Luego se debe agregar a éste resultado 5 meses que es el equivalente a \frac{5}{12}. Por lo anterior ahora sí sustituimos los valores de cada una de las variables, lo cual nos da:
\begin{align*}
i&=\left(\frac{25000}{22000}\right)^{\frac{7}{2}+\frac{5}{12}}-1\\
&=\left(\frac{25000}{22000}\right)^{\frac{47}{12}}-1\\
&=0.64
\end{align*}
Por lo tanto, el valor de la tasa de interés es: $i=64 \%$
Ejercicio. Dado un capital inicial de \$1200 pesos, un monto total de \$3500, con una tasa efectiva trimestral de 3.77%, calcular $t$.
Solución
La ecuación que se aplicará para este caso es la siguiente:
$$t=\frac{\log M-\log K}{\log(1+i)}$$
Sustituyendo cada una de las variables que se conocen, nos queda:
\begin{align*}
t&=\frac{\log 3500-\log 1200}{\log(1+0.0377)}\\
&=\frac{0.464886}{0.016071}\\
&=28.92554
\end{align*}
Es importante señalar que el resultado está dado en trimestres, puesto que la tasa con la que se están realizando los cálculos es efectiva trimestral. Por otra parte cada año tiene 4 trimestres, entonces cuando el resultado excede a 4, entonces la cifra expresada en años, se obtiene del resultado de $t=28.92554$ el cual, se divide entre 4, entonces se tiene $\frac{28.92554}{4}=7.231385$ de donde se obtienen los 7 años.
Ahora como no se suele expresar 0.231385 meses, lo que se va a hacer es multiplicar por 12(porque el año tiene 12 meses), esto es: $(0.231385)(12)=2.77662$ que es de dónde se obtienen los 2 meses.
Por último para saber los días, multiplicamos la cifra de (77662)(30) por que un mes tiene 30 días, hacemos uso de la cifra de $(0.77662)(30)=23.2986$, resultado a partir del cual se obtiene el dato de los 23 días.
Por lo tanto, el resultado obtenido se interpreta como 7 años, 2 meses y 23 días.
Ejercicio. El banco ABC lanzo un programa especial de ahorro, mediante el cual está ofreciendo un rendimiento del 8% efectivo anual en los primeros 6 meses de inversión, posteriormente menciona que se dejan sus recursos otros 6 meses les otorgara el 10% de rendimiento, y por último ofrece una tasa del 12% para el resto del tiempo que el cliente mantenga depositado su dinero en el banco. ¿Cuánto dinero acumulara dicho cliente, si el día de hoy depositó $10,000 y planea dejarlo en el banco por un tiempo de un año y ocho meses?
Solución
Es un caso en el que las tasas de interés cambian durante los 2 primeros semestres, y al final se mantiene constante a partir del 3er semestre. En tal caso el tiempo total que permanecerá invertido el dinero será por 1 año y 8 meses. Lo cual implica lo siguiente:
Monto al final del primer semestre queda determinado por
$M=10000(1+0.08)^{\frac{1}{2}}$
El monto que se tiene en el segundo semestre es:
$M=[10000(1+0.08)^{\frac{1}{2}}](1+0.10)^{\frac{1}{2}}$
Por último, el monto obtenido al termino del año con 8 meses
$M=[[10000(1+0.08)^{\frac{1}{2}}](1+0.10)^{\frac{1}{2}}](1+0.12)^{\frac{8}{12}}$
$M= 11,754.93$
Más adelante…
En este tema, se abordó el modelo de Interés compuesto, mediante el cual se observa el fenómeno mediante el cual, una cantidad de dinero invertida, prestada o depositada en alguna institución bancaria, nos genera intereses con el paso del tiempo, y no sólo eso, sino que, en el caso particular del interés compuesto, los intereses generan más intereses. Éste proceso que se acaba de estudiar de forma implícita es conocido también como acumulación. Con éste modelo nos da una herramienta muy importante para poder tomar mejores decisiones respecto al uso de los recursos que se tienen de manera personal, comercial, social, etc. porque nos sirve para saber cuánto se puede llegar a ahorrar en el caso de querer adquirir un bien o servicio, o unas vacaciones, o comprar un vehículo. En otro caso, cuánto se va a tener que pagar por un cierto préstamo, o incluso cuánto se requiere tener para llevar a cabo un proyecto que requiere cierto financiamiento (es un tipo de préstamo que permite tener recursos, por ejemplo, inversionistas) para conocer cuánto es lo que se va a deber en el futuro.
En el siguiente capítulo, se abordará el proceso inverso que acabamos de estudiar, esto es, describir la metodología que nos permita conocer el valor que al día de hoy tiene una obligación futura, fenómeno que dentro de las Matemáticas Financieras se le conoce como Valor Presente.
- Ir a Matemáticas Financieras
- Entrada anterior: Historia, antecedentes, interés simple
- Entrada siguiente
