Introducción
De acuerdo con el material que se ha presentado, destacan dos personajes importantes, el prestamista y el deudor, el primero se priva de sus recursos, mientras que el segundo hace uso de ellos, a cambio de una recompensa que llamamos interés, el cual es otorgado al prestamista, dicha cantidad le será entregada luego de haber transcurrido una cierta cantidad de tiempo el cual, es pactado por los involucrados y determinará la duración que tenga la operación. De esta forma se puede decir que existe una igualdad en cuanto a los derechos del deudor que es recibir recursos, así como éste último tiene la obligación de entregar los intereses acordados al término del plazo. Para modelar este fenómeno, se hace uso del modelo de interés compuesto, que matemáticamente es una ecuación que implica una igualdad, la cual consiste que un monto es igual la cantidad inicial que fue prestada más los intereses acordados. Al hacerlo queda establecida y garantizada la relación de las obligaciones y los derechos, de manera tal que, se garantiza equidad en la operación entre las partes involucradas.
Ecuación de valor
La ecuación que se va a estar usando para garantizar la igualdad que se acaba de describir, recibe el nombre de ecuación de valor, que permite garantizar la igualdad que relaciona los derechos del deudor al adquirir los recursos, y éste tiene la obligación de hacer el pago del capital inicial más los intereses, cada uno de ellos sabiendo el valor que adquieren en una misma fecha de valuación, dicha fecha es conocida como fecha focal.
Formalizando el concepto de ecuación de valor, será definido como «La representación matemática de una operación financiera o comercial que hace iguales los derechos y las obligaciones contraídos por las partes, valuados a la misma fecha» (Cánovas T., 2004, pág. 106).
Lo anterior, regularmente se formaliza a través de un contrato, donde queda asentados principalmente los valores de la ecuación, el capital inicial, la duración que va a tener el préstamo, los intereses que van a ser pagados, así como la forma, y la tasa de interés.
Reglas para su construcción
Los modelos que se han estado utilizando para este tipo de situaciones son ecuaciones de valor, cada una de ellas tienen en común las siguientes características:
- En el primer lado de la igualdad se escriben los derechos del prestamista y en el otro lado se anotan las obligaciones del deudor, siempre debe ser así, puede darse el caso en el que estén al revés, pero resulta indistinto, dependerá del cálculo que uno necesite obtener para encontrar el valor deseado.
- Los cálculos que se realicen siempre deben estar calculados en una misma fecha de valuación, una misma fecha focal.
- Las ecuaciones de valor, son usadas regularmente cuando se desea estar trabajando con pagos, que están indicados en fechas distintas y éstas a su vez están relacionadas con pagos que se realizarán en diferentes plazos, de allí surge la necesidad de fijar una fecha focal en la que se estarán valuando todas las operaciones que se vayan a realizar.
Su aplicación es muy frecuente, cuando se renegocian las deudas, esto ocurre cuando el deudor no le es posible terminar de pagar su deuda, en el tiempo acordado; y es en ése momento que se recurre al uso de una ecuación de valor.
Por citar un ejemplo: una persona va a depositar sus ahorros a un banco, y de acuerdo a los temas que se han estado revisando, ésta persona va a ganar un rendimiento, una cantidad extra de lo que acaba de depositar, generada por los intereses que el banco está obligado a pagar, por dejar sus ahorros un cierto periodo de tiempo. Dicha cantidad extra, es el producto de multiplicar su capital inicial por una tasa de interés cada cierto número de periodos. En este caso, aparece una cierta obligación del banco para su cliente que es la de pagar intereses, así como el cliente tiene que dejar de tener sus ahorros por una cierta cantidad de tiempo, de forma implícita, existe una relación costo-beneficio entre ambas partes.
Ejercicios resueltos
Ejercicio. Una persona desea adquirir a crédito un terreno con un valor de \$140 000. Según los cálculos que tiene considerados con sus ahorros tiene la cantidad de \$70 000, la cantidad que va a necesitar es de \$70 000. La persona firma un contrato en donde estipula que realizará pagos de la siguiente forma:
- Dar un enganche de \$70 000
- Hacer un pago por la cantidad de \$30 000, el 15 de abril de 2023
- Realizar otro pago de \$27 000 el día 15 de julio del mismo año.
- La fecha de valuación es el día 15 de enero de 2023, día en que inicia el contrato y es la fecha en la que comienza a hacer pagos comenzando por cubrir el enganche.
Se desea saber ¿cuánto es lo que le falta por pagar para saldar la deuda el día 10 de agosto de 2023? y la tasa pactada es del \1.8% efectivo mensual.
Solución

En la imagen se muestra la forma en que se realizarán los pagos, y de ella se puede obtener la siguiente ecuación de valor:
$$140,000=70,000+30,000v_{0.018}^3+27,000v_{0.018}^6+Xv_{0.018}^7.$$
En este ejemplo, se muestran los conceptos que caracterizan a una ecuación de valor. Para su mejor comprensión, se señalan cada uno de ellos en la siguiente imagen.
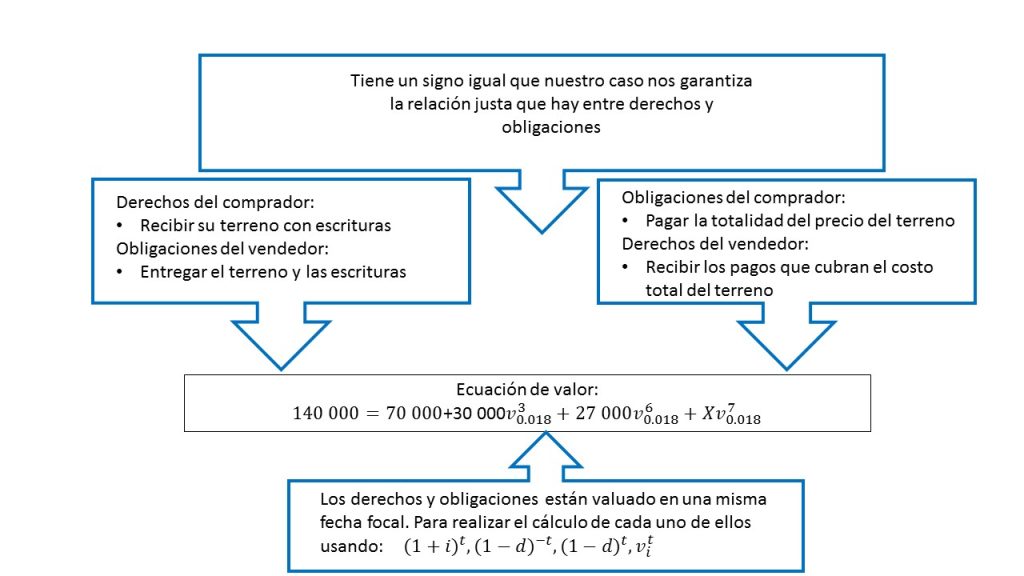
Una vez analizados cada uno de los elementos que conforman a nuestra ecuación de valor se calculará el valor del último pago.
\begin{align*}
X&=\frac{140 000-70 000-30 000v_{0.018}^3-27 000_{0.018}^6}{v_{0.018}^7}\\
&=\frac{140 000-70 000-30 000(0.947887)-27 000(0.0.898490)}{0.987490}\\
&=\frac{140 000-70 000-28436.61648-24259.23470}{0.987490}\\
&=\frac{17304.14882}{0.987490}\\
&=17523.36613.\\
\end{align*}
Por lo tanto, el último para que se realizará, se hará por una cantidad de \$17,523.37.
El señor Luis, quiere comprar un paquete de viaje de vacaciones para su familia, con todo pagado, y lo piensa sacar a crédito, por lo que el día de hoy 10 de enero de 2022, con un valor es de \$160 mil pesos, hace el contrato aportando una cantidad de \$80 mil pesos, considera hacer otra aportación \$30 mil pesos el 10 de abril, otro pago de \$25 mil el 10 de agosto, y un último pago liquidando su deuda el 10 de diciembre. Se requiere saber ¿De cuánto es el último pago, si la agencia de viajes otorga el crédito con una tasa de interés del 1.9% efectiva mensual?
Solución
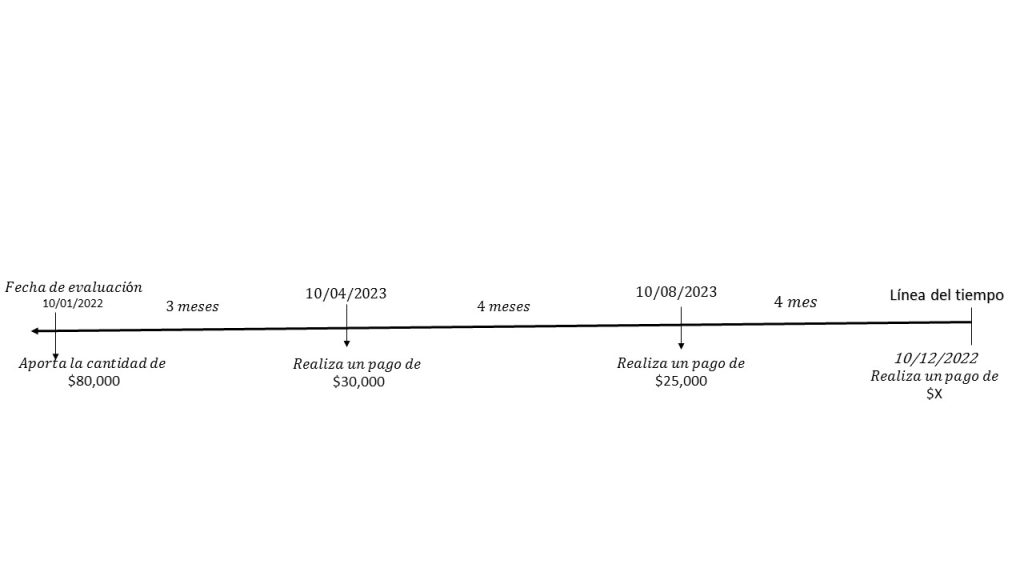
Nuevamente, en la imagen se representa la forma en que van a realizarse los pagos, y nos permite construir la ecuación de valor que se va a manejar para encontrar la solución.
$$160,000=80,000+30,000v_{0.019}^3+25,000v_{0.019}^7+Xv_{0.019}^{11}.$$
\begin{align*}
X&=\frac{160,000-80,000-30,000v_{0.019}^3-25,000_{0.019}^7}{v_{0.019}^11}\\
&=\frac{160,000-80,000-30,000(0.94509)-25,000(0.0.8765581)}{0.81298777}\\
&=\frac{160,000-80 000-28,352.97942-21,913.95274}{0.81298777}\\
&=\frac{29733.06784}{0.81298777}\\
&=36,572.58933.\\
\end{align*}
Por lo tanto, el último a realizar será por la cantidad de \$36,572.59.
Más adelante…
Con las herramientas que hasta el momento se han abordado, ya se cuenta con el material suficiente para entrar con temas de mayor complejidad, ya que de cierta forma hace que utilicemos todas las metodologías se han estado desarrollando. Dicho teme es el de las anualidades, cuya importancia dentro de las matemáticas financieras es fundamental, toda vez que suelen ser muy utilizadas en muchas de las operaciones de crédito, económicas, dentro de las operaciones financieras o comerciales.
Entradas relacionadas
- Ir a Matemáticas Financieras
- Entrada anterior
- Entrada siguiente
