Introducción
Las anualidades, son una herramienta de vital importancia dentro de las matemáticas financieras, ya que su uso está presente en la gran mayoría de operaciones o transacciones económicas, financieras y/o comerciales. En este apartado, se dará a conocer el concepto de anualidad, sus principales características, tipos de anualidades, así como algunas reglas elementales para su uso de forma correcta.
Definición de anualidad
Siempre que se quiera adquirir algún producto, algún bien como lo es una casa, y se quiera hacer dicha compra a crédito, va a ser necesario un contrato en el que quedaran especificados una serie de pagos, con cierta temporalidad, a una cierta tasa de interés, mediante los cuales se irá pagando dicha deuda, o dicho crédito.
En este apartado, se analizarán los modelos matemáticos más usados, mejor conocidos con el nombre de anualidades, las cuales se utilizan para poder resolver los problemas que acaban de mencionar.
Se entenderá por anualidad, al conjunto de pagos que se realizarán de forma periódica durante un cierto tiempo, que tendrá la misma periodicidad que los pagos, haciendo el uso del modelo de interés compuesto. Sin embargo, cabe hacer mención que el nombre de anualidades, no necesariamente va a implicar siempre que el pago va a ser anual (cada año), sino que también van a darse casos en los que los pagos serán semanales, diarios, mensuales, bimestrales, trimestrales, semestrales, etc.
Algunos ejemplos de anualidades son: los pagos a crédito de electrodomésticos, pagos de renta de una casa o departamento, pagos de crédito de un automóvil, pago de pensiones, pago de primas de algún tipo de seguro (vida, daños, de gastos médicos mayores, etc.)
Tipos de anualidades
- Anualidades ciertas. Son aquellas en las que los pagos no tienen ningún tipo de restricción, condición u ocurrencia de evento para que se lleven a cabo los pagos. por tal motivo quedan establecidas los pagos y el plazo.
- Anualidades contingentes. Son conocidas por que existe alguna condición o cierta contingencia o evento tenga que pasar, tenga que cumplirse para poder llevarse a cabo los pagos, un ejemplo que describe claramente ésta situación son los pagos generados por una renta vitalicia en la que sólo podrán hacerse los pagos, una vez que el cónyuge muera.
- Anualidades ordinarias vencidas. En este tipo de anualidad, los pagos se realizan al final de cada periodo, durante el plazo que se haya pactado que duraría la operación, también es conocida como anualidad ordinaria.
- Anualidades anticipadas. En ésta anualidad, es muy semejante a la anterior, la única diferencia es que los pagos se realizan al inicio de cada periodo, de cierta forma se entendería que los pagos se hacen por adelantado.
- Anualidades diferidas. Son anualidades que se caracterizan por tener u otorgar un periodo de «gracia», que es un cierto tiempo que pasa antes de que comiencen a efectuarse los pagos.
- Perpetuidad. Son anualidades en las que los pagos que en teoría, «nunca» dejan de hacerse, Un ejemplo que muestra más claramente su uso, es la creación de un fondo de una beca para un estudiante, la cual una vez que dicho alumno culmine sus estudios, siga habiendo recursos suficientes para que pueda ser asignada a otro estudiante, de manera tal que siempre existan fondos suficientes para seguir apoyando a estudiantes.
- Anualidades crecientes. Su principal característica es que los pagos van incrementando una determinada cantidad cada periodo. Un ejemplo de su utilización se da cuando una empresa desea adquirir con el paso del tiempo, la modernización de su maquinaria, más actual y por ende más eficiente.
- Anualidad decreciente. Es análoga a la anterior, solo que en lugar de aumentar una cierta cantidad cada periodo, ésta va disminuyendo.
- Anualidad pagadera p-veces al año. Se caracterizan por fijar una cantidad que se pagará durante un año, o en su caso durante los años subsecuentes, hasta cubrir la totalidad de la deuda.
- Anualidad continua. Se caracterizan por tener pagos muy pequeños, durante periodos muy pequeños, de forma continua, con el fin de liquidar un crédito o u acumular una cierta cantidad al término de un cierto lapso de tiempo.
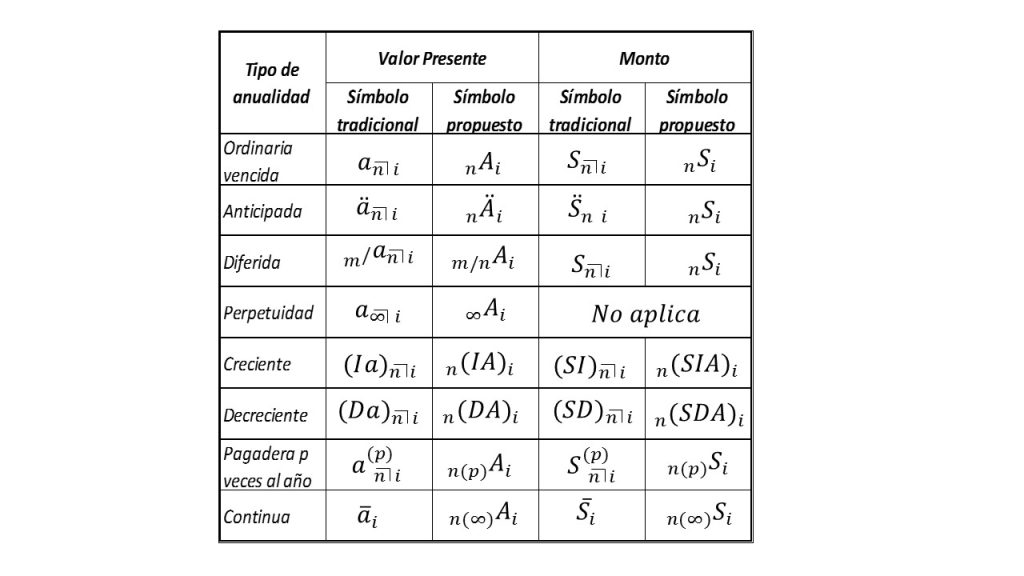
Elaboración propia, basado en Cánovas T. Fundamentos de Matemáticas Financieras, Ed. Trillas, pag. 116.
Anualidades ordinarias vencidas
Como se mencionó, son el tipo de anualidad, en el que los pagos se realizan al final de cada periodo. Su construcción es realizada a partir del caso de \$1.00, durante un tiempo de n-periodos, el cual queda descrito en la siguiente imagen:
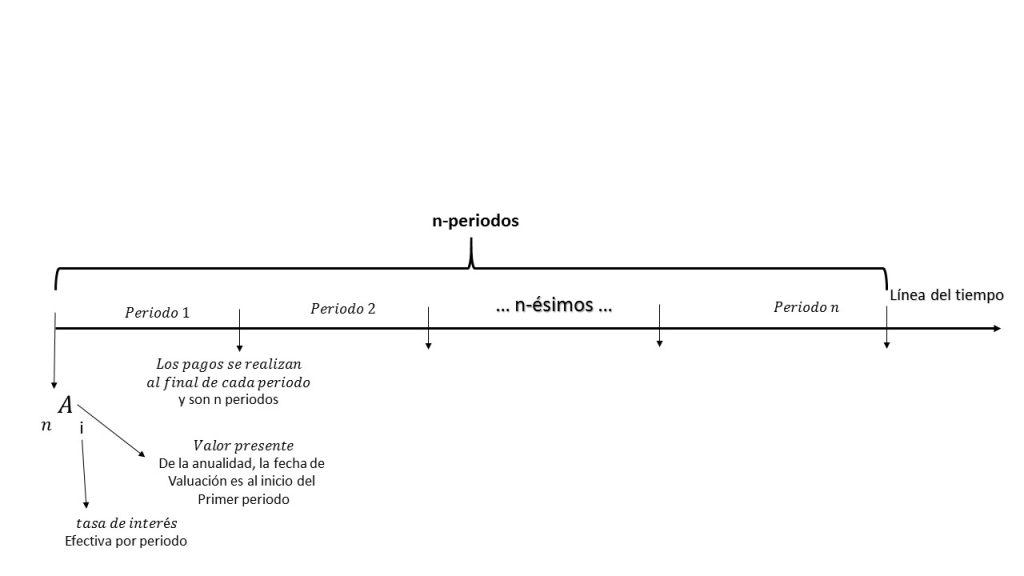
Considerando la imagen anterior, se denotará una anualidad vencida como:
$$\prescript{}{n}{\mathbf{A}}_i=1v_i^1+1v_i^2+1v_i^3+…+1v_i^{n-1}+1v_i^n$$
$$\prescript{}{n}{\mathbf{A}}_i=1(v_i^1+v_i^2+v_i^3+…+v_i^{n-1}+v_i^n).$$
Ésta expresión, puede ser vista como una progresión geométrica, tal como se muestra a continuación:
$$\prescript{}{n}{\mathbf{A}}_i=\frac{v_i^1-v_i^nv_i^1}{1-v_i^1}=\frac{v_i^1-v_i^{n+1}}{1-v_i}$$
$$=\frac{v_i(1-v_i^n)}{1-v_i}.$$
Sustituyendo el valor de $v$ se tiene:
$$=\frac{\frac{1}{(1+i)}(1-v_i^n)}{1-\frac{1}{(1+i)}}$$
$$=\frac{\frac{1}{(1+i)}(1-v_i^n)}{\frac{1+i-1}{(1+i)}}$$
$$=\frac{\frac{1}{(1+i)}(1-v_i^n)}{\frac{i}{(1+i)}}.$$
Cancelando la expresión $\frac{1}{(1+i)}$ en el numerador como en el denominador, se tiene:
$$\prescript{}{n}{\mathbf{A}}_i=\frac{1-v^n}{i}.$$
Dicha expresión, es la que se va a estar utilizando para hacer el cálculo del valor presente de una anualidad vencida. Al igual que los modelos que anteriormente se han estado construyendo, obedece a las mismas reglas del modelo de interés compuesto.
Es necesario notar que, cuando en el modelo el valor de $n=1$ se tiene el caso de una anualidad de un sólo pago, y al ser sólo un pago, no podría ser considerada como una anualidad, sin embargo, se sigue cumpliendo que el valor presente sea igual a $v$. Generalizando la expresión anterior, dejando de considerar \$1 como valor del capital que se está manejando, y asignando un valor \$X, entonces la expresión queda de la siguiente forma:
$$V=Xv_i^1+Xv_i^2+Xv_i^3+…+Xv_i^{n-1}+Xv_i^n$$
$$V=X(v_i^1+v_i^2+v_i^3+…+v_i^{n-1}+v_i^n).$$
Como ya sabemos, la expresión entre paréntesis equivale a una anualidad vencida, entonces realizamos la sustitución de forma tal que nos queda:
$$V=X\prescript{}{n}{\mathbf{A}}_i.$$
Por otra parte, para calcular el monto de una anualidad vencida se hace lo siguiente:
$$\prescript{}{n}{\mathbf{S}}_{i}=1(1+i)^{n-1}+1(1+i)^{n-2}+…+1(1+i)^{2}+1(1+i)^{1}+1$$
$$\prescript{}{n}{\mathbf{S}}_{i}=\frac{1-(1+i)^{n-1}(1+i)}{1-(1+i)}$$
lo anterior, es posible ya que, de forma análoga al valor presente, se está trabajando con progresiones geométricas, por lo que al aplicar sus propiedades se obtiene el siguiente resultado:
$$\prescript{}{n}{\mathbf{S}}_{i}=\frac{(1+i)^n-1}{i}.$$
Es necesario mencionar que, la expresión anterior, considera con un capital de \$1, aplicando de forma más general el modelo quedaría:
$$M=X\prescript{}{n}{\mathbf{S}}_{i}=X\left(\frac{(1+i)^n-1}{i}\right).$$
Ejercicios resueltos
Ejercicio. Es muy común, en la práctica tener casos en los que combinen mensualidades con pagos anuales. Lo anterior es una práctica común que tiene la intención de reducir la cantidad de intereses que se está pagando. Por ejemplo, el siguiente ejercicio:
Don Raúl, desea adquirir un vehículo último modelo, motivo por el cual solicita un autofinanciamiento, el cual requiere que realice un pago del 30% de enganche. El valor total de la unidad cuesta \$400,000. La forma en que Don Raúl desea pagarlo es cubrir el enganche, sacarlo a 60 mensualidades con una tasa del 20% pagadera mensualmente. Además, quiere aportar la cantidad de $20,000 cada cinco años de forma vencida. Ante este contexto, don Raúl desea saber ¿Cuánto va a tener que pagar de mensualidad?
Solución
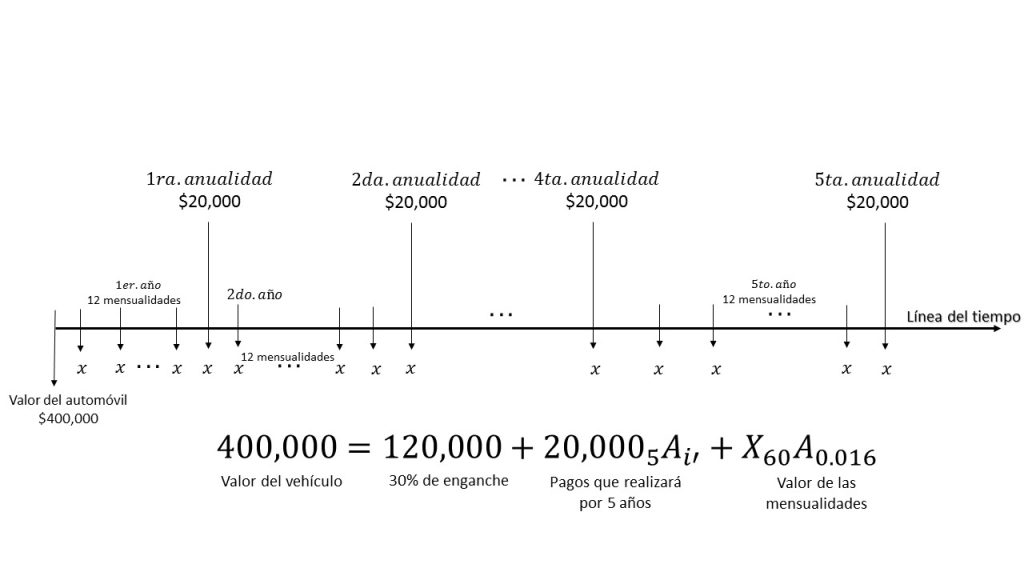
Elaboración propia, basado en Fundamentos de Matemáticas Financieras, Cánovas T. Ed. Trillas, pag. 119.
$$\frac{i^{12}}{12}=\frac{0.2}{12}=0.016667.$$
Este resultado es el que va a ser utilizado para calcular: $\prescript{}{60}{\mathbf{A}}_{0.016}.$
Luego, para calcular $\prescript{}{5}{\mathbf{A}}_{i}$, es necesario obtener la tasa efectiva anual denotada por $i’$, que al mismo tiempo es una tasa equivalente a la tasa equivalente efectiva mensual que se acaba de calcular.
$$(1+i’)=(1+0.016667)^{12}$$
$$i’=(1.016667)^{12}-1=0.219391.$$
Calculamos el valor de $X$, para hacerlo se despeja dicha variable de la ecuación de valor:
$$X=\frac{400,000-120,000-20,000\prescript{}{5}{\mathbf{A}}_{0.219391}}{\prescript{}{60}{\mathbf{A}}_{0.0167}}$$
$$X=\frac{180,000-20,000(2.867373)}{37.74424}$$
$$X=3249.57.$$
Por lo tanto, la mensualidad le queda en \$3249.57 durante 60 meses, con sus respectivas aportaciones de \$20,000 al final de cada año, éstas realizadas de forma vencida, es decir, al final de cada año.
Ejercicio. Una empresa de hilos, compró maquinaria a crédito con un valor de \$500,000, los pagos los va a realizar de forma mensual, con un valor de \$4,000, la duración de la deuda fue de 18 meses, la tasa que están manejando es de 1.35% efectiva mensual. La empresa quiere liquidar dicha deuda lo antes posible. Dado que tiene en puerta un negocio de gran importancia, pretende pagar la totalidad del adeudo dentro de un mes, situación que comunica el vendedor de la maquinaria, para poder renegociar el monto que le resta y que no tenga que estar pagando tanto interés. Se requiere saber ¿cuál es la cantidad que hace falta por pagar dentro de un mes, para liquidar completamente la deuda?
Solución
$$X=4,000+4,000\prescript{}{17}{\mathbf{A}}_{0.0135}$$
$$X=4,000+4,000(15.885371)=67,541.48$$
por lo tanto, la cantidad que debe de pagar es de \$67,541.48.
Más adelante…
Se abordarán el tema de anualidades anticipadas, que como su nombre lo dice los pagos se harán al inicio de cada periodo, las cuales se verá que son de vital importancia, ya que muchas operaciones de seguros hacen uso de ellas. Su funcionamiento resultará de forma muy parecida a las anualidades anticipadas, pero de forma inversa.
Entradas relacionadas
- Ir a Matemáticas Financieras
- Entrada anterior
- Entrada siguiente
