Introducción
Se seguirá viendo resultados y problemas relacionados con la razón cruzada, en esta entrada se abordará los Puntos autocorrespondientes y la regla geométrica de la falsa posición.
Puntos Autocorrespondientes
Sean $A,B,C$ y $A’,B’,C’$ dos conjuntos de puntos en una misma línea recta, por ende para un punto cualquiera $D$ en la recta le corresponde un punto $D’$ que nos dará como resultado $\{ ABCD \}=\{ A’B’C’D’ \}$.
Problema. El problema cae en la siguiente incógnita ¿Existirá un punto $D$ que se corresponda al mismo?, de tal forma que $\{ ABCD \}=\{ A’B’C’D \}$.
Demostraremos que puede haber uno, dos o ningún punto, a este punto existente se le llamará punto autocorrespondiente con respecto a las dos razones cruzadas.
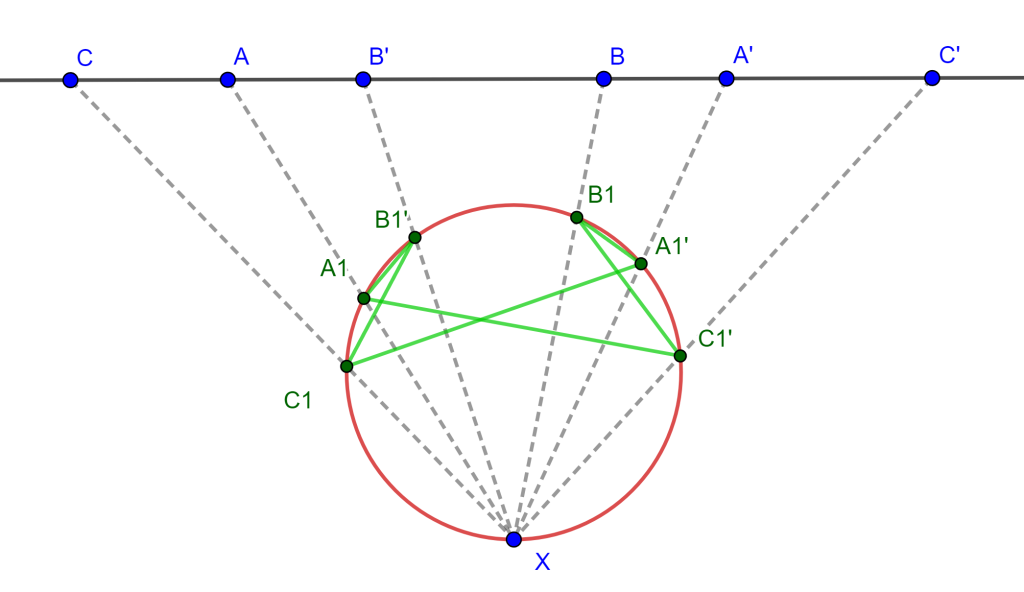
Solución. Trácese cualquier circunferencia en el plano y tómese un punto $X$ en esta, y únanse los puntos $A,B,C,A’,B’,C’$ a $X$, y las intersecciones con la circunferencia y estas rectas se denotarán como $A_1, B_1, C_1, A_1′, B_1′, C_1’$.
Notese que tenemos un hexagono inscrito con lados $A_1C_1’$, $A_1B_1’$, $C_1A_1’$, $B_1C_1’$, $B_1A_1’$, $B_1’C_1$, y la existencia del punto $D$ depende de que este hexágono cumpla el Teorema de Pascal.
El Teorema de Pascal dice que «Los puntos de intersección de los lados opuestos de un hexágono inscrito en una circunferencia son colineales». Es de esta forma que la intersección de $A_1B_1’$ y $A_1’B_1$ se cortan en $P$, $B_1’C_1$ y $B_1C_1’$ en $Q$, $A_1C_1’$ y $A_1’C_1$ en $R$, de esta forma se tiene la recta $PQ$ la cual corta a la circunferencia en $D_1$ y $E_1$.
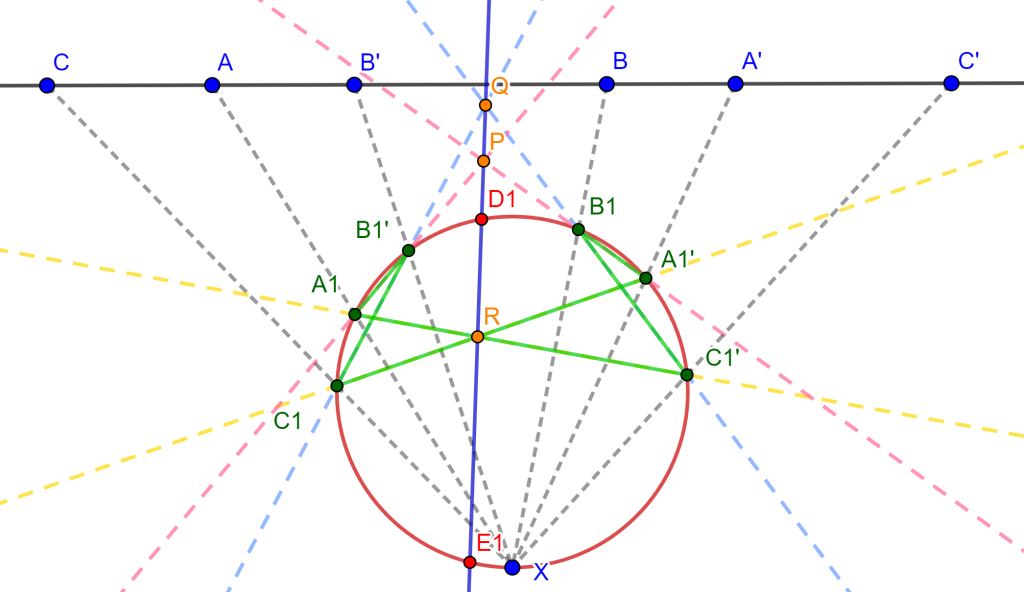
Ahora las rectas $XD_1$ y $XE_1$ cortarán la recta de los haces en los puntos $D$ y $E$ correspondientemente, estos son los dos puntos buscados. Sea $S$ la intersección de $PQ$ con $A_1A_1’$.
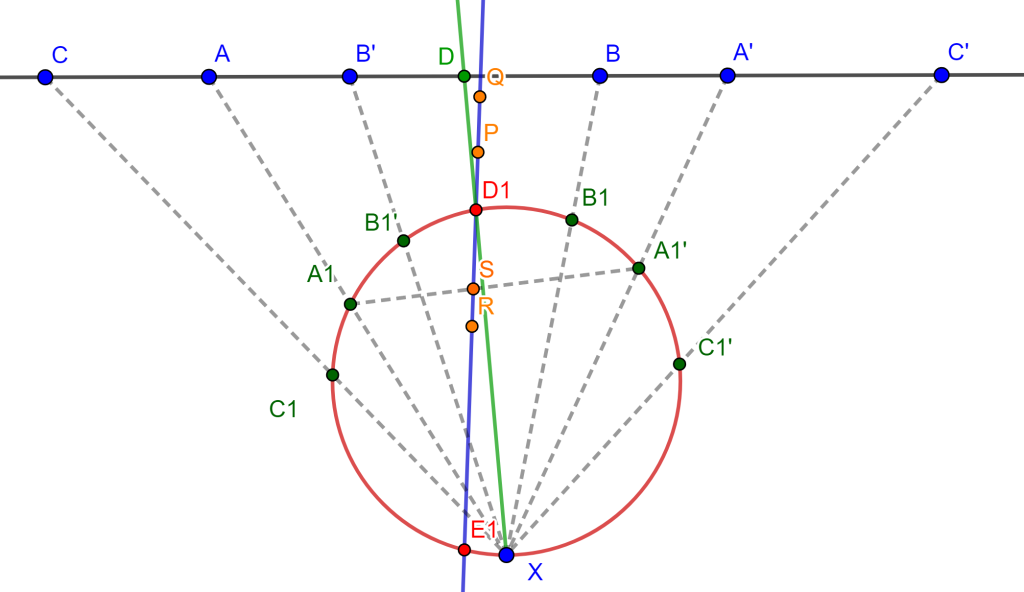
Entonces se tienen las siguientes igualdades:
$\{ ABCD \}=X\{ A_1B_1C_1D_1\}$
por propiedad 1 de razón cruzada de la circunferencia se tiene:
$X\{ A_1B_1C_1D_1\}=A_1’\{ A_1B_1C_1D_1\}$
Por razón cruzada se tiene:
$A_1’\{ A_1B_1C_1D_1\}=\{SPRD_1\}= A_1\{ A_1’B_1’C_1’D_1 \}$
Por razón cruzada por la circunferencia:
$A_1\{ A_1’B_1’C_1’D_1 \} = X\{ A_1’B_1’C_1’D_1\} = \{ A’B’C’D \}$
Por lo tanto, $\{ ABCD \}=\{ A’B’C’D \}$ y es equivalente para $E$.
$\square$
Ahora, si $PQ$ es tangente a la circunferencia, solo existirá un punto autocorrespondiente, y si la recta $PQ$ no corta a la circunferencia, entonces no existe ningún punto autocorrespondiente.
Regla geométrica de la falsa posición
Esta regla viene del siguiente problema:
Problema. Construir un triángulo el cual sus lados pasan por los vértices de un triángulo dado y cuyos vértices se encuentran en los lados de otro triángulo dado.
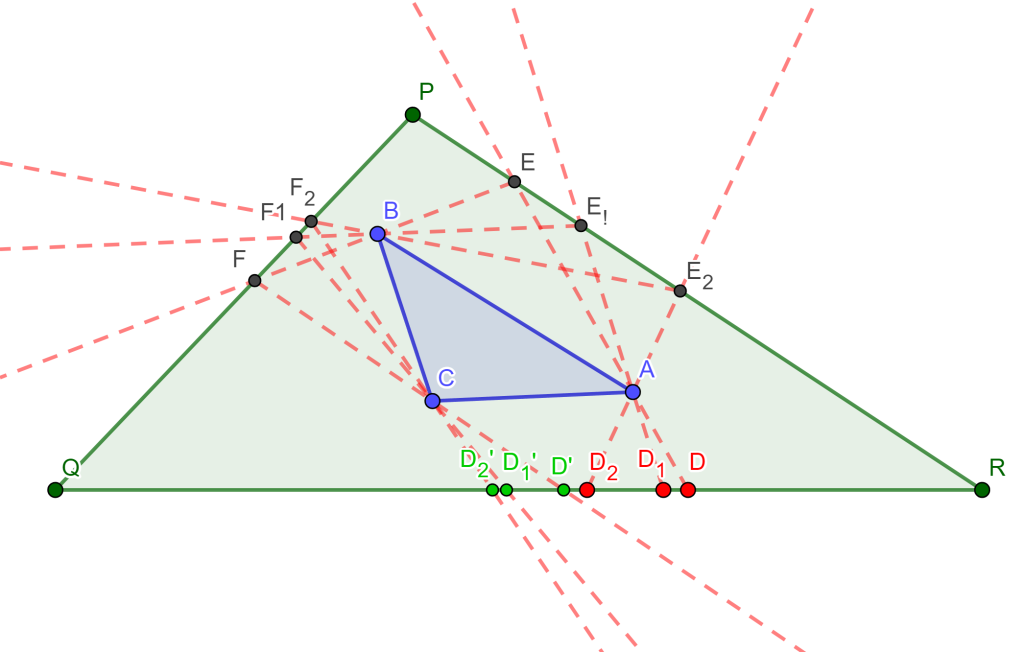
Solución. El triángulo a encontrar debe tener sus lados, los cuales deben pasar por los vértices del triángulo $PQR$, y sus vértices en los lados del triángulo $ABC$.
Sea un punto $D$ en $QR$, trácese $DA$ que corte a $PR$ en $E$, $EB$ que corte $PQ$ en $F$, y $FC$ que corte a $QR$ en $D’$, si $D$ y $D’$ son el mismo ya tendríamos el triángulo buscado. Por lo cual se vuelve a hacer lo mismo para $D_1$ obteniendo $D_1’$ y $D_2$ obteniendo $D_2’$, si estos son puntos iguales ya lo tendríamos resuelto, pero no es así, por ende se construirán los puntos autocorrespondientes a partir de $D,D_1,D_2,D’,D_1′,D_2’$.
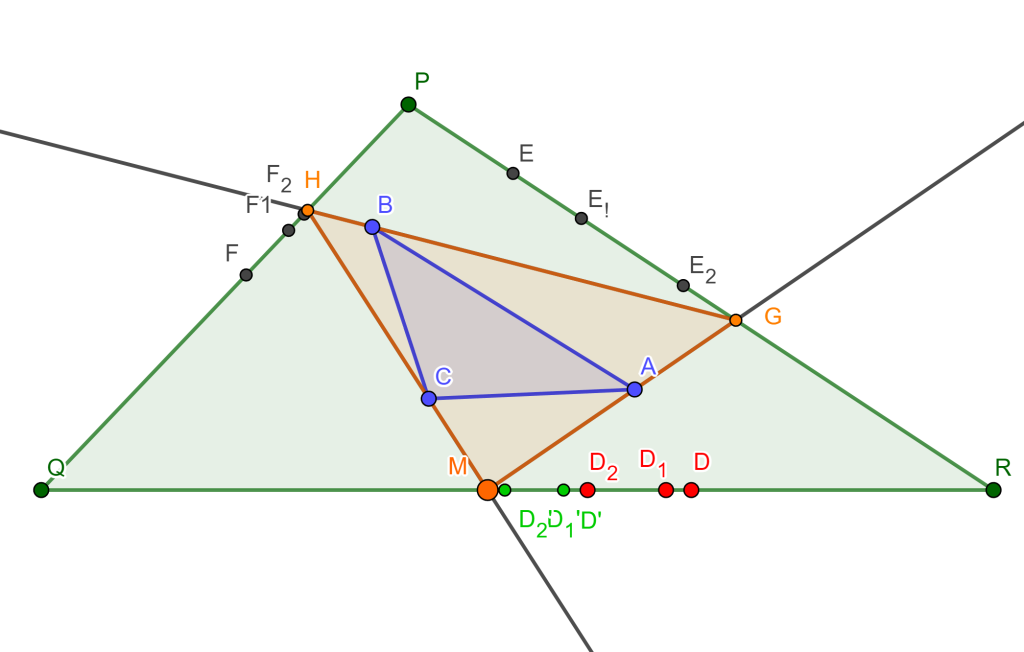
Si estos puntos $M$ y $N$ existen, y pasamos por uno de ellos, en este caso $M$ para construir el triángulo buscado, nos daríamos cuenta de que regresamos a $M$ y estaría solucionado, pero como menciones estos triángulos existen si existen los puntos autocorrespondientes.
$\square$
Más adelante…
Se verán tres teoremas importantes respecto al tema de Razón Cruzada, los cuales son Teoremas de Pascal, Brianchon y Pappus.
Entradas relacionadas
- Ir a Geometría Moderna II
- Entrada anterior del curso: Razón cruzada en la circunferencia
- Siguiente entrada del curso: Teoremas de Pascal, Brianchon y Pappus