Introducción
Definición. La circunferencia de similitud (o de homotecia) de dos circunferencias no concéntricas, es la circunferencia que tiene como diámetro el segmento que une sus centros de similitud (o de homotecia).
Definición.
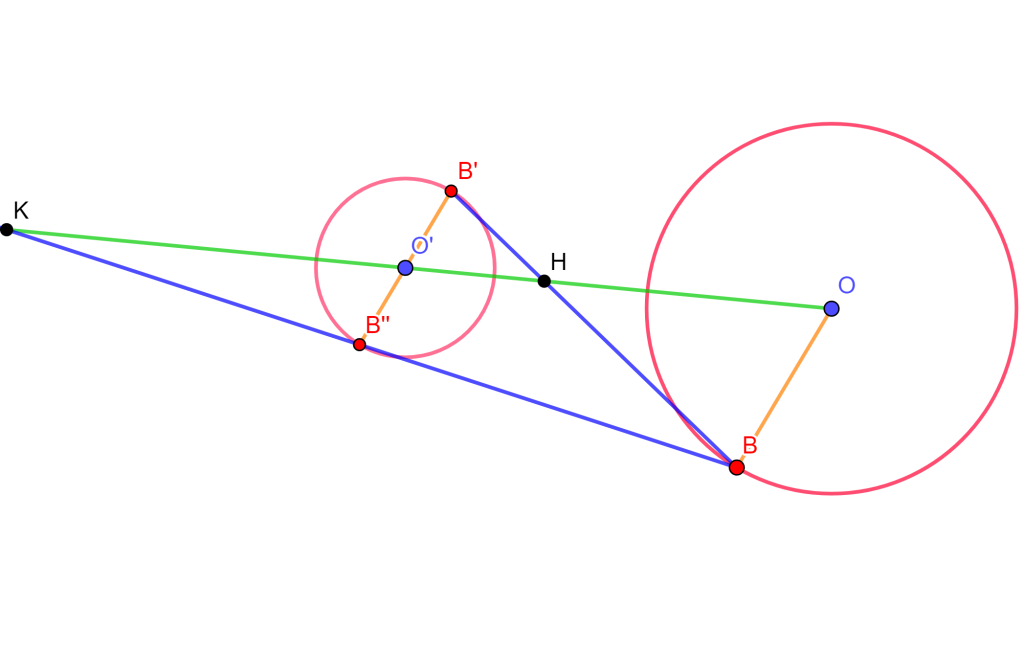
Sean dos círculos no concéntricos. Se unirá el centro $O$ de uno de ellos a cualquier punto $B$ de su círculo, no colineal con los centros. Si dibujamos el diámetro del otro círculo paralelo a $OB$ entonces interseca la circunferencia en $B’$ y $B$.
Si hacemos que $BB’$ y $BB’$$’$ intersequen la línea de los centros de las circunferencias en $H$ y $K$, entonces $\triangle OBH \sim \triangle O’B’H$, y $\triangle OBK \sim \triangle O’B’$$’K$. De lo anterior los dos circulos son homoteticos y $H$ y $K$ los centros de Homotecia.
Teorema. La circunferencia de similitud de dos círculos no concéntricos es el lugar geométrico de los puntos, tales que la razón de las distancias entre sus centros es igual a la razón entre sus radios.
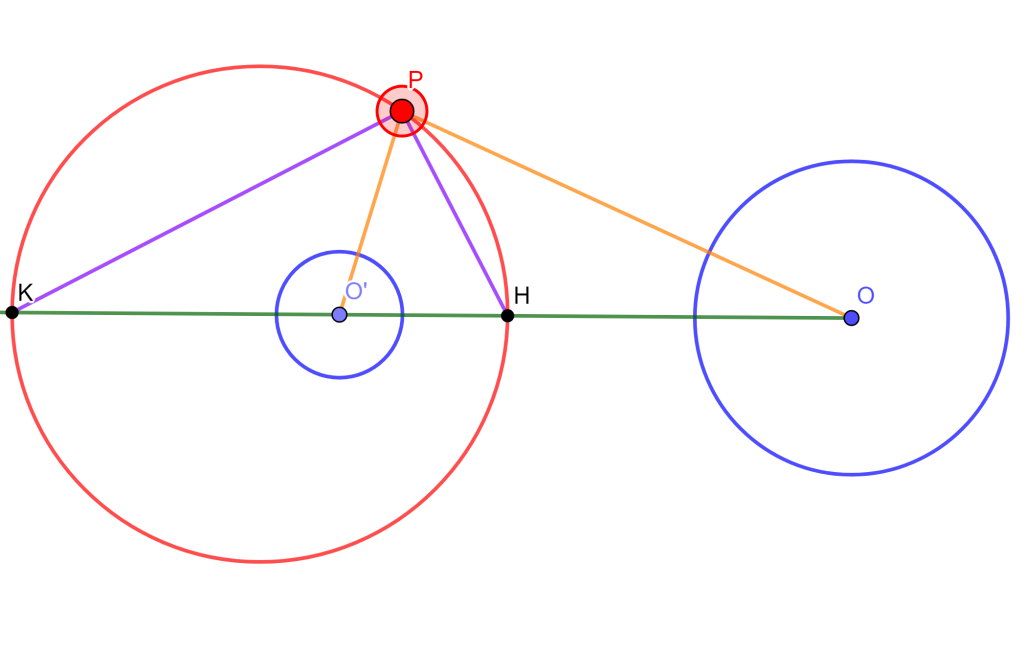
Demostración. Sean dos circunferencias dadas $\mathcal{C}_1(O,r)$ y $\mathcal{C}_2(O’,r’)$, donde existen $H$ y $K$ sus centros de Homotecia.
$\boldsymbol{\Rightarrow} ]$
Sea un punto $P$ talque $PO:PO’ =r:r’$, esto se ve como $\frac{PO}{PO’}=\frac{r}{r’}$. Queremos demostrar que $P$ es un punto del lugar geométrico.
Entonces como $KO:KO’=OH:HO’=r:r’$, se sigue que $K$ y $H$ son puntos del lugar geometríco. Ahora como $PO’:PO=r’:r$ entonces $PO’:PO=KO’:KO=O’H:HO.$
Por el Teorema de la Bisectriz interna y externa $PH$ y $PK$ son las bisectrices interior y externa del angulo $\angle O’PO$. Entonces $PH$ y $PK$ son perpendiculares, y $P$ está en el círculo de similitud. $\square$
$\boldsymbol{\Leftarrow} ]$
Supongamos que $P$ está en el círculo de similitud. En la línea de los centros tenemos $O’$$’$ tal que $PH$ bisecta el angulo $O’PO’$$’$.
Entonces, ya que $PH$ y $PK$ son perpendiculares y que bisecan los ángulos interior y exterior en $P$ del triángulo $\triangle O’$$’PO’$, entonces
$O’$$’H:HO’=-O’$$’K:KO’$
además
$OH:HO’=-OK:KO’$
Entonces
$HO’$$’:O’$$’K=HO:OK$
Entonces $O’$$’$ coincide con $O$. Se tiene que $PO:PO’=r:r’$ $\square$
Del teorema anterior es necesario que $r \neq r’$, ya que si $r=r’$ syss $r/r’ =1$. Si dos círculos son iguales, su círculo de similitud degenera en la mediatriz del segmento que une sus centros y la línea al infinito.
Observación. la generalización del concepto de circunferencia de similitud es la circunferencia de Apolonio.
Teorema. El lugar geométrico de los puntos, cuyas razones de sus distancias a dos puntos fijos es una constante, es la circunferencia de Apolonio.
Sean los puntos fijos $O$ y $O’$ la razón de sus distancias a $P$ desde $O$ y $O’$, sea $r:r’$. Construiremos círculos con centros en $O$ y $O’$ cuyos radios tengan la razón $r:r’$. Por la demostración anterior, el lugar geométrico de los puntos $P$ es el círculo de similitud.
Más adelante…
Ya analizadas las circunferencias coaxiales, se verán aplicaciones al cuadrilátero completo.
Entradas relacionadas
- Ir a Geometría Moderna II
- Entrada anterior del curso: Familias coaxiales
- Siguiente entrada del curso: Aplicaciones al cuadrilátero completo
