Introducción
En las siguientes entradas, comenzaremos a desarrollar de lleno la noción de integral de Lebesgue. Es entonces natural pensar en los conjuntos en donde una función $f:\mathbb{R}^n\to \mathbb{R}$ es «aproximadamente constante», es decir, para un $a\in \mathbb{R}$ arbitrario, conjuntos de la forma $$E=\{x\in \mathbb{R}^n \ | \ a\leq f(x)<a+\varepsilon \}.$$
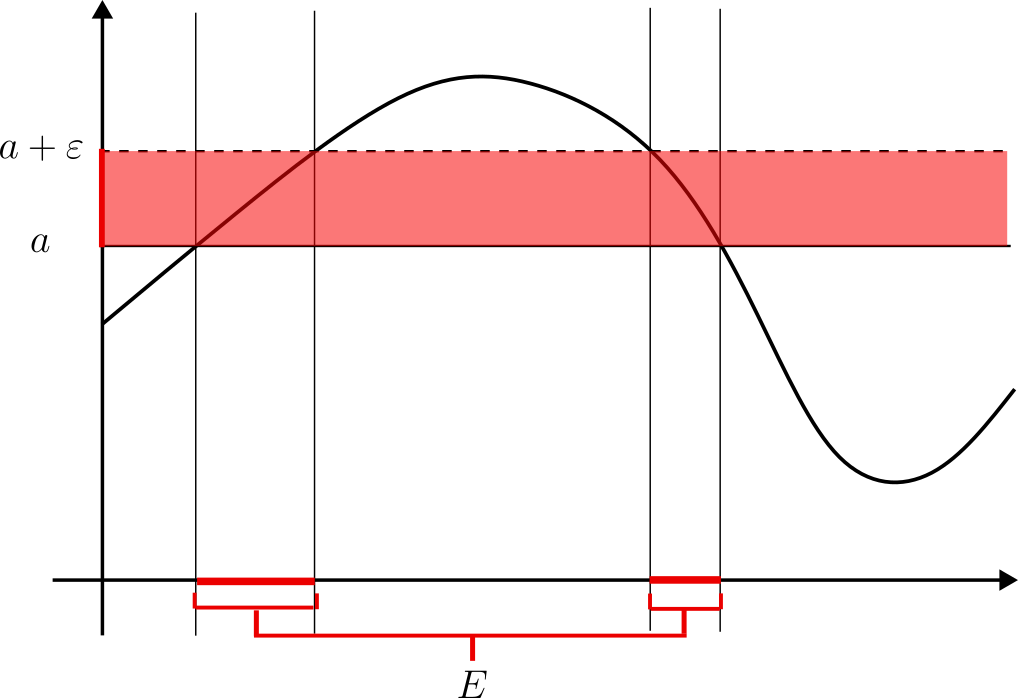
De forma intuitiva, la contribución del conjunto $E$ a la integral debería ser aproximadamente $a\lambda(E)$. Para que esto tenga sentido, es necesaro que el conjunto $E$ sea medible. Si lo anterior se satisface para cualquier $a\in \mathbb{R}$ y $\varepsilon>0$ diremos (provisionalmente) que la función es medible.
Antes de continuar, será muy útil permitir que $f$ tome los valores «extendidos» $\infty$ y $-\infty$. Podemos pensar que $f(x)=\infty$ significa que $f$ «es arbitrariamente grande en $x$» mientras que $f(x)=-\infty$ significa que $f$ es «arbitrariamente negativa en $x$».
La ventaja principal de esta notación es que nos permite trabajar con límites (posiblemente infinitos) de una manera unificada. Por ejemplo, si $\{ f_k \}_{k=1}^{\infty}$ es una sucesión de funciones tales que $\lim_k f_k(x)$ existe para todo $x\neq 0$ y $f_k(0)=k$ para todo $k$, conviene pensar que la sucesión $\{ f_k \}_{k=1}^{\infty}$ converge puntualmente a una función $f$ con $f(0)=\infty$. A la hora de integrar, esto a veces nos permitirá lidiar con singularidades sencillas de sucesiones de funciones.
Para ello, hace falta extender nuestra noción de números reales y su aritmética a $-\infty$ e $\infty$.
Reales extendidos
Definición. Definimos el sistema de numeros reales extendidos: $$[-\infty,\infty]:=\mathbb{R}\cup\{ -\infty \}\cup \{\infty \}.$$
(De manera formal $\infty,-\infty$ son solamente símbolos, pero conviene pensarlos con su significado usual de cantidades arbitrariamente grandes y arbitrariamente negativas respectivamente. La diferencia es que ahora los pensamos como números sobre los que podemos definir operaciones aritméticas explícitas).
Trabajaremos con las siguientes convenciones (todas éstas son naturales y están formuladas para ser compatibles con las nociones clásicas de límites infinitos): Para cualesquiera $x\in \mathbb{R}$, $0<a\leq \infty$, $-\infty\leq b <0$ convenimos:
\begin{align*}
-\infty < x &< \infty, \\
x + \infty &= \infty, \\
\infty + \infty &= \infty, \\
a\cdot \infty &= \infty, \\
b\cdot \infty &= -\infty.
\end{align*}
Y similarmente
\begin{align*}
x – \infty &= -\infty, \\
-\infty – \infty &= -\infty, \\
a\cdot -\infty &= -\infty, \\
b\cdot -\infty &= \infty.
\end{align*}
Las expresiones $0\cdot \pm \infty$ y $\infty – \infty$ permanecen indefinidas (aunque ocasionalmente, conviene definir la primera como cero).
Dado $A$ un subconjunto de números reales extendidos, convenimos:
- $\sup A:=\infty$ si $\infty\in A$.
- $\sup A= -\infty$ si $A={ -\infty }$.
- $\sup A:= \sup (A\setminus { -\infty})$ si $\infty \notin A$ y $A\neq \{ -\infty\}$ (es decir, el supremo usual de un conjunto de números reales, posiblemente $\infty$ si el conjunto es no acotado).
Las convenciones para $\inf A$ son análogas.
Los límites se trabajan de forma idéntica. Dada una sucesión $\{ a_k\}_{k=1}^{\infty}$ de números reales extendidos:
- Decimos que $\lim_{k\to \infty}a_k=a$, $a\in \mathbb{R}$, si $a_k\in \mathbb{R}$ salvo una cantidad finita de $k$ y $\lim_{k\to \infty}a_k=a$ en el sentido usual (omitiendo los valores extendidos de la sucesión).
- Como es usual, decimos que $\lim_{k\to \infty}a_k=\pm \infty$ si $\forall M\in \mathbb{R}$ positivo $\exists N\in \mathbb{N}$ tal que $\pm x_m>M$ $\forall m\geq N$.
Las convenciones para límites de funciones $\lim_{x\to a }f(x)$ son análogas.
Como consecuencia de nuestras convenciones, es inmediato verificar que los límites extendidos heredan las propiedades de sus contrapartes reales, por ejemplo las referentes a sumas y productos de límites.
El siguiente caso es particularmente frecuente. También es una muestra de las ventajas de adoptar la notación de números reales extendidos.
Observación. Toda sucesión monótona (creciente o decreciente) de números extendidos tiene un límite.
Demostración. En efecto, sea $a_1\leq a_2\leq a_3\leq \dots$ una sucesión monótona creciente de números extendidos. Si la sucesión es acotada y no todos los términos son $-\infty$, se reduce al caso real en el que sabemos que la sucesión converge (y de hecho, converge a su supremo). Si $a_k=-\infty $ para todo $k$, claramente $\lim_{k\to \infty} a_k=-\infty$. Si la sucesión no es acotada entonces $\lim_{k\to \infty} a_k=\infty$. El caso decreciente es similar.
$\square$
Ejemplo. Considera la sucesión de funciones $f_k=k\chi_{[-\frac{1}{k},\frac{1}{k}]}$ (donde $\chi_A$ representa la función característica del conjunto $A$: $\chi_A(x)=1$ si $x\in A$ y $\chi_A(x)=0$ en otro caso). Para cualquier $x\neq 0$, eventualmente $f_k(x)=0$, así que $\lim_{k\to \infty} f_k(x)=0$. Como $f_k(0)=k$ para todo $k$, naturalmente $\lim_{k\to \infty} f_k(0)=\infty$. Concluimos que la sucesión converge puntualmente (en el sentido extendido) a la función
\begin{equation*}
f(x)=
\begin{cases}
0 & \text{si } x \neq 0 \\
\infty & \text{si } x=0 \in \mathbb{R}\setminus\mathbb{Q}.
\end{cases}
\end{equation*}
$\triangle$
Funciones medibles
Ya podemos dar una definición bastante general de función medible sobre conjuntos arbitrarios con alguna $\sigma$-álgebra asociada.
Definición. Sea $f:X\to[-\infty,\infty]$ donde $X$ es un conjunto. Dada $\mathcal{M}$ una $\sigma$-álgebra sobre $X$, decimos que $f$ es $\mathcal{M}$-medible si $\forall t\in [-\infty, \infty]$, el conjunto $$\{ x \ | \ f(x)\leq t\}=f^{-1}([-\infty,t])\in \mathcal{M}.$$
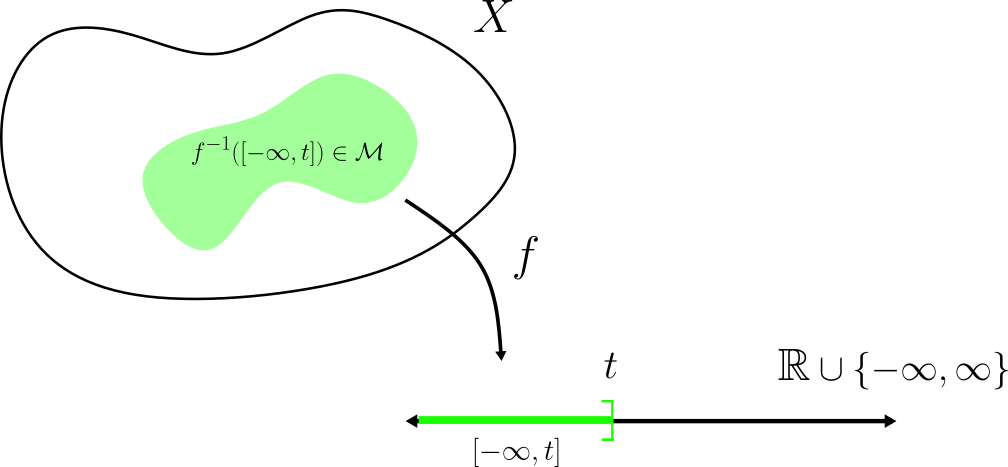
Es conveniente pensar en las funciones medibles como aquellas que «tienen la suficiente estructura como para ser integradas». Si bien definimos el concepto de función medible con toda generalidad (que es necesario para desarrollar nociones de integración sobre espacios «muy generales»), casi siempre trabajaremos con los siguientes dos casos:
- Si $X=\mathbb{R}^n$ y $\mathcal{M}=\mathcal{L}$ diremos que la función es Lebesgue-medible o simplemente medible.
- Si $X=\mathbb{R}^n$ y $\mathcal{M}=\mathcal{B}$ diremos que la función es Borel-medible.
Observación. Como $\mathcal{B}\subseteq \mathcal{L}$, toda función Borel-medible es Lebesgue-medible.
Equivalencias
Como veremos a continuación, existen varias definiciones equivalentes de función medible. Nos moveremos entre ellas con frecuencia.
Proposición. Sea $\mathcal{M}$ una $\sigma$-álgebra sobre $X$ y $f:X\to [-\infty,\infty]$. Entonces $f$ es $\mathcal{M}$-medible si y sólo si cualquiera de las siguientes condiciones se satisface:
- $f^{-1}([-\infty,t])\in \mathcal{M}$ para todo $t\in[-\infty,\infty]$.
- $f^{-1}([-\infty,t))\in \mathcal{M}$ para todo $t\in(-\infty,\infty]$.
- $f^{-1}([t,\infty])\in \mathcal{M}$ para todo $t\in[-\infty,\infty]$.
- $f^{-1}((t,\infty])\in \mathcal{M}$ para todo $t\in[-\infty,\infty)$.
- $f^{-1}({ \pm \infty } )\in \mathcal{M}$ y $f^{-1}(E)\in \mathcal{M}$ para cualquier conjunto de Borel $E\subseteq\mathbb{R}$.
Demostración. Las equivalencias 1$\iff $4 y 2$\iff $3 son inmediatas al tomar complementos.
Notemos que $f(x)<t$ si y sólo si existe algún número racional $r\in \mathbb{Q}$ tal que $f(x)\leq r <t$, de donde $$f^{-1}([-\infty,t))=\bigcup_{r\in \mathbb{Q},r<t}f^{-1}([-\infty,r]).$$ Por la cerradura bajo uniones numerables en $\mathcal{M}$, se sigue la implicación 1$\implies$2.
Análogamente podemos ver que $$f^{-1}([-\infty,t])=\bigcap_{r\in \mathbb{Q},r>t}f^{-1}([-\infty,r)).$$
Lo que demuestra similarmente que 2$\implies$1. Esto concluye las equivalencias 1 $\iff$ 2 $\iff$ 3 $\iff$ 4.
La implicación 5$\implies$1 es obvia pues $E=[-\infty,t]$ es de Borel para todo $t$.
Veamos entonces que las condiciones 1-4 implican la condición 5.
Al tomar $t=-\infty$ en 1, se sigue que $f^{-1}({ -\infty})\in \mathcal{M}$. Similarmente al tomar Al tomar $t=\infty$ en 3, se sigue que $f^{-1}({ \infty})\in \mathcal{M}$.
Definamos $\mathcal{S}$ como $$\mathcal{S}=\{ E\subseteq \mathbb{R} \ | \ f^{-1}(E)\in \mathcal{M}\}.$$
Es fácil verificar directamente que $\mathcal{S}$ es una $\sigma$-álgebra. Para lo que resta, es suficiente probar que $\mathcal{S}$ contiene a los conjuntos abiertos de $\mathbb{R}$, pues en ese caso se tendría $\mathcal{B}\subseteq \mathcal{S}$ lo que completa la implicación.
Observemos primero que cualquier abierto de $\mathbb{R}$ es unión numerable de intervalos abiertos. En efecto, dado $U\subseteq \mathbb{R}$ abierto y $s\in
U$, podemos encontrar números racionales $p_s,q_s$ tales que $s\in(p_s,q_s)\subseteq U$. Luego $$U=\bigcup_{s\in U}(p_s,q_s).$$ Es unión numerable de intervalos abiertos.
Por lo anterior y la cerradura de $\sigma$-álgebras bajo uniones numerables, es suficiente probar que los intervalos abiertos son elementos de $\mathcal{S}$. Esto es inmediato pues podemos expresar:
$$f^{-1}((a,b))=f^{-1}([-\infty,b)])\cap f^{-1}((a,\infty]).$$
Que resulta un elemento de $\mathcal{M}$ pues $f^{-1}([-\infty,b)])$ y $f^{-1}((a,\infty])$ son elementos de $\mathcal{M}$ por las condiciones 2 y 4.
$\square$
Algunos ejemplos de funciones medibles
Veamos algunos ejemplos clásicos de funciones medibles. En la sección de ejercicios se detallan algunos otros.
Proposición. Toda función continua $f:\mathbb{R}^n\to \mathbb{R}$ es Borel-medible. En particular es Lebesgue-medible.
Demostración. En la entrada pasada probamos que si $f:\mathbb{R}^n\to \mathbb{R}$ es continua y $A\in \mathcal{B}_1$ $\implies$ $f^{-1}(A)\in \mathcal{B}_n$. Por la proposición anterior, esto garantiza que $f$ es Borel-medible.
$\square$
Proposición. Si $f:\mathbb{R}\to [-\infty,\infty]$ es una función monótona (creciente o decreciente), entonces $f$ es Borel-medible.
Demostración. En efecto, si $f$ es monótona, la imágen inversa de cualquier semirrecta $[t,\infty]$ es algún intervalo, posiblemente abierto, cerrado, semiabierto o semicerrado; pero en todo caso un conjunto de Borel.
$\square$
Otro ejemplo muy importante son las funciones características. Éstas son esenciales para definir el concepto de función simple, que a su vez es fundamental para definir la integral de Lebesgue de una función. La demostración es muy sencilla y se queda como tarea moral.
Proposición. Sea $X$ un conjunto y $\mathcal{M}$ una $\sigma$-álgebra sobre $X$. Si $A\in \mathcal{M}$, entonces, la función característica \begin{equation*} \chi_A(x) =
\begin{cases}
1 & \text{ si } x\in A \\
0 & \text{ si } x \notin A
\end{cases}
\end{equation*} Es $\mathcal{M}$-medible.
$\square$
Ejemplo (funciones medibles sobre subconjuntos). Sea $\mathcal{M}$ una $\sigma$-álgebra sobre $X$ y $f:X\to [-\infty,\infty]$ una función $\mathcal{M}$-medible sobre $X$. Es fácil ver que para cualquier $E\in \mathcal{M}$, la restricción de $f$ sobre $E$, $f_{|E}:E\to [-\infty,\infty]$, es una función $\mathcal{M}_E$-medible ($\mathcal{M}_E$ denota la restricción de $\mathcal{M}$ sobre $E$).
$\triangle$
Más adelante…
Veremos más propiedades de las funciones medibles. En particular veremos que la clase de funciones medibles es cerrada bajo una gran cantidad de operaciones aritméticas y tomas de límite.
Tarea moral
- Verifica las propiedades pendientes de los números reales extendidos.
- Sea $X$ un conjunto y $\mathcal{N}$ una $\sigma$-álgebra sobre $X$. Verifica que si $A\in \mathcal{M}$ $\implies$ $\chi_A$ es $\mathcal{M}$-medible. ¿Qué pasa si $A\notin \mathcal{M}$?
- Sea $X$ un conjunto y $\mathcal{M}=\{X,\emptyset \}$. Demuestra que las únicas funciones $\mathcal{M}$-medibles son las funciones constantes.
- Sea $X$ un conjunto y $\mathcal{M}=2^X$. ¿Qué funciones son $\mathcal{M}$-medibles?
- Sea $X$ un conjunto y $\mathcal{M}$ una $\sigma$-álgebra sobre $X$. Sea $A\in \mathcal{M}$ y $f:A\to [-\infty,\infty]$ una función definida sobre $E$. Demuestra que $f$ es $\mathcal{M}_A$-medible $\iff$ $f^{-1}([-\infty,t])\in \mathcal{M}$ para todo $t\in[-\infty, \infty]$ $\iff$ $f^{-1}(\pm \infty)\in \mathcal{M}$ y $f^{-1}(K)\in \mathcal{M}$ para todo $K\subseteq \mathbb{R}$ conjunto de Borel.
- Decimos que una función $f:\mathbb{R}\to \mathbb{R}$ es continua a pedazos, si existen puntos $\dots <x_{-2}<x_{-1}<x_0<x_1<x_2<\dots$ tales que $f$ es continua en $(x_k,x_{k+1})$ para todo $k\in \mathbb{Z}$. Prueba que toda función continua a pedazos es Borel-medible. Prueba también que es Lebesgue-medible.
