Introducción
En esta entrada conoceremos más propiedades de los espacios métricos compactos. Veremos qué ocurre cuando les es aplicada una función continua. Esto nos relacionará dos espacios métricos entre sí a través de los subconjuntos. Podremos concluir información acerca de la imagen de una función cuando ciertas condiciones se cumplen. Comencemos con la siguiente:
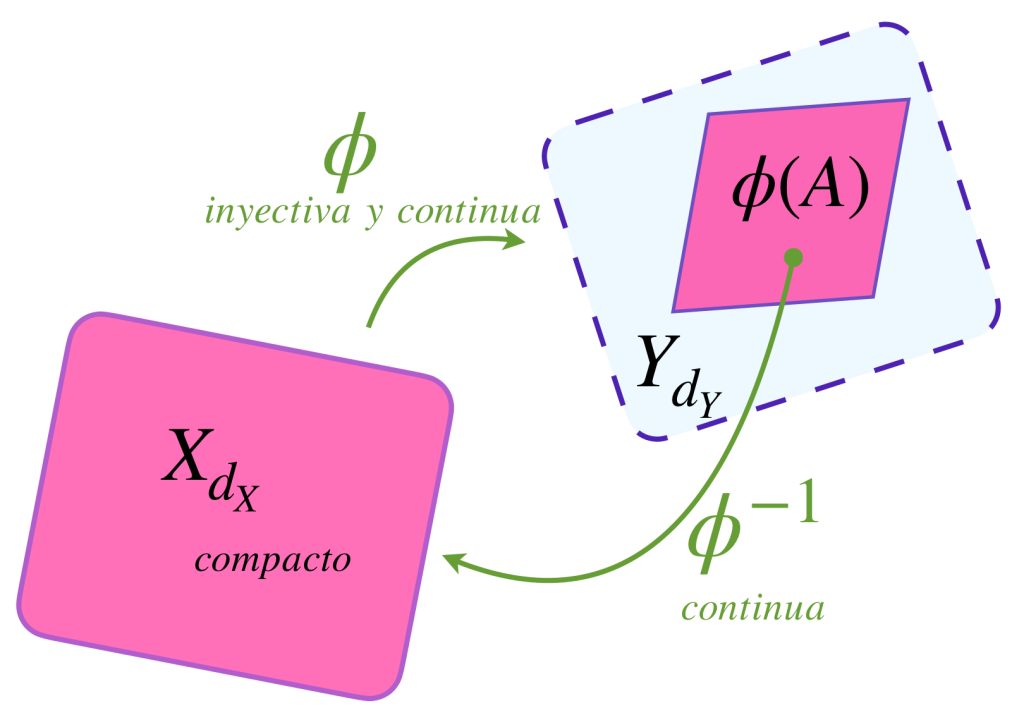
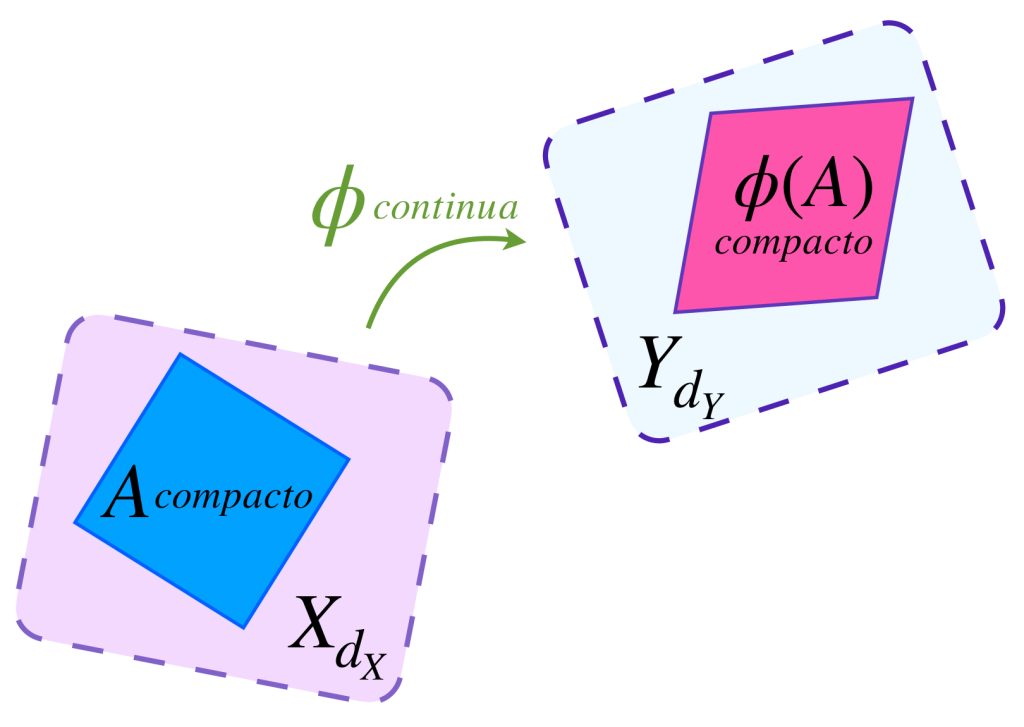
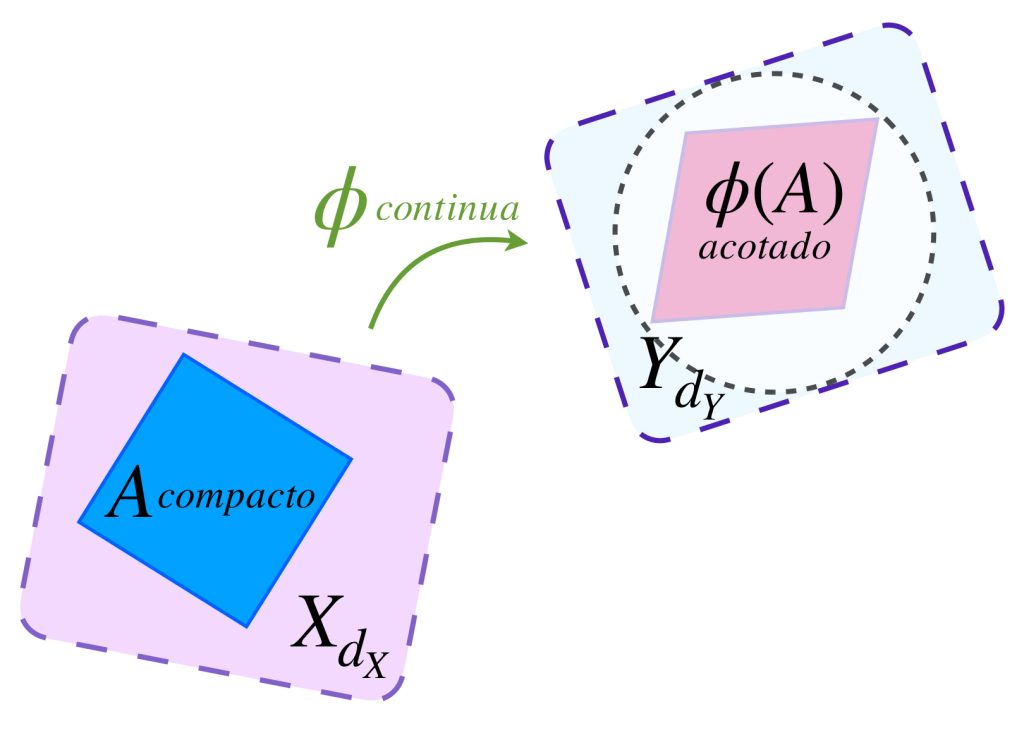
Proposición: Sean $(X,d_X)$ y $(Y,d_Y)$ espacios métricos. Si $\phi:X \to Y$ es una función continua y $A \subset X$ es compacto, entonces la imagen de $A$ bajo $\phi$, es decir, $\phi(A),$ es un conjunto compacto en $(Y,d_Y).$
Demostración:
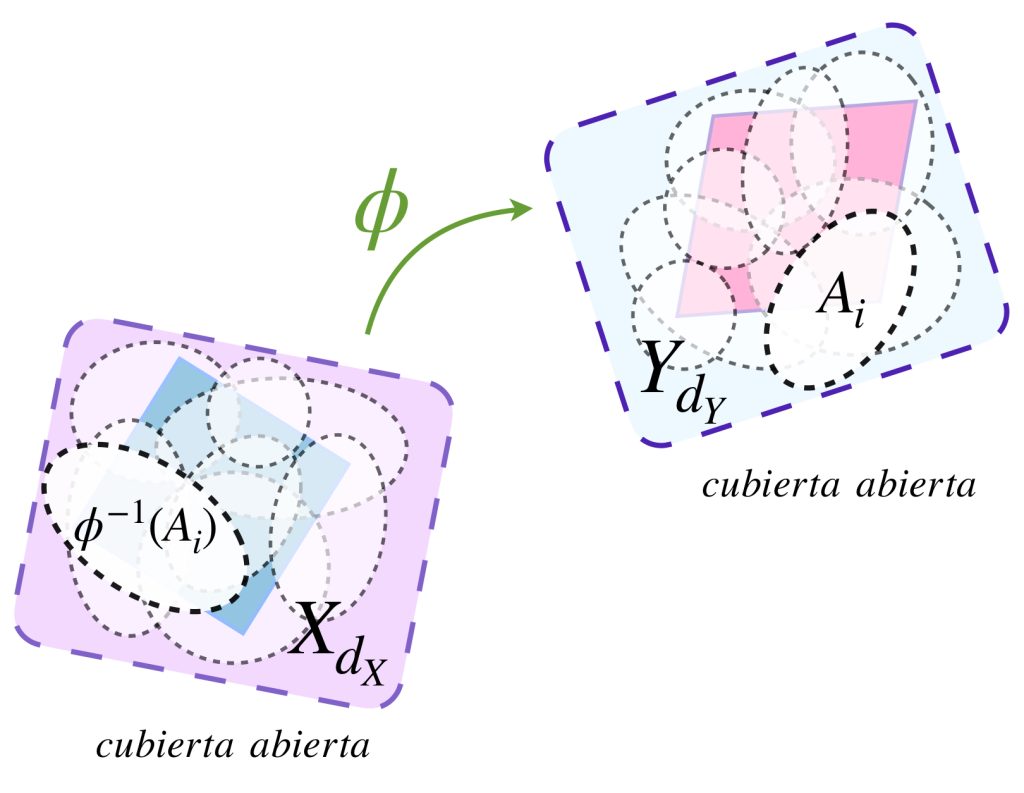
Sea $\mathcal{C}= \{A_i: i \in \mathcal{I}\}$ una cubierta abierta de $\phi (A)$. Como $\phi$ es continua entonces la imagen inversa de $A_i,$ es decir, el conjunto $\phi ^{-1}(A_i), i \in \mathcal{I}$ es un conjunto abierto en $X$. No es difícil probar que $\{\phi ^{-1}(A_i):i \in \mathcal{I}\}$ es una cubierta abierta de $A.$ (Ejercicio).
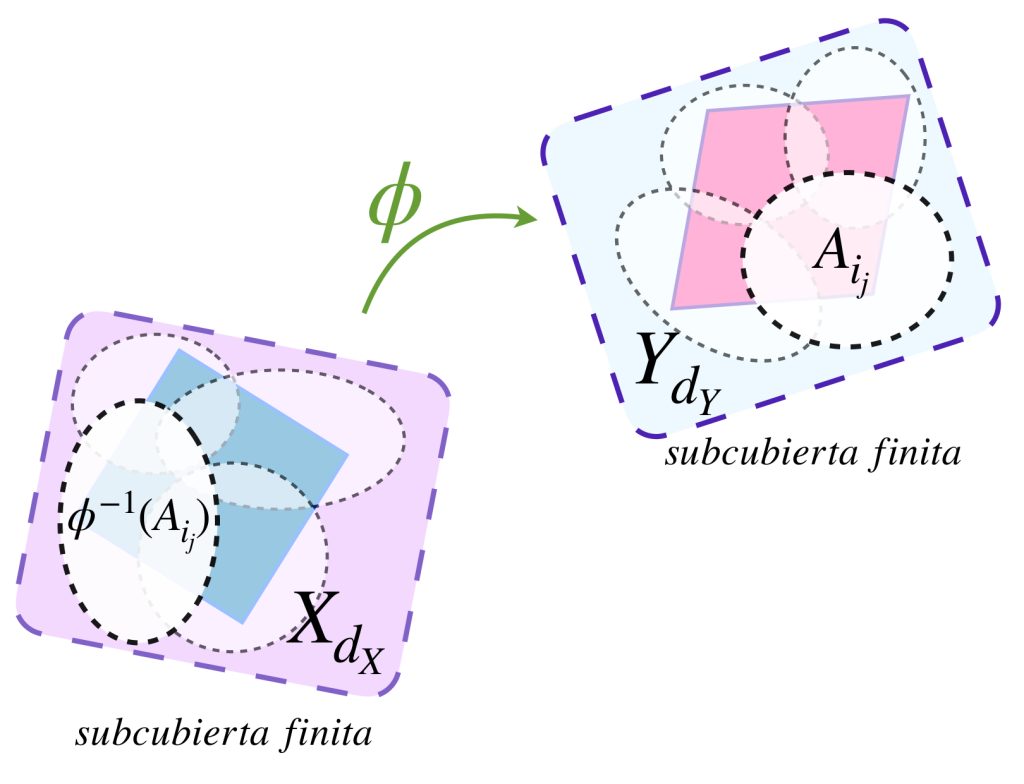
Como $A$ es compacto, entonces existe una subcubierta finita $\{\phi ^{-1}(A_{i_1}),\phi ^{-1}(A_{i_2}),…,\phi ^{-1}(A_{i_m}) \}$ con $m \in \mathbb{N}$ tal que $A \subset \underset{1\leq j \leq m}{\bigcup}\phi ^{-1}(A_{i_j}).$ Esto significa que $\{A_{i_1},A_{i_2},…,A_{i_m}\}$ es una subcubierta en $Y$ de $\mathcal{C}$ para $\phi (A)$. (¿Por qué?) Por lo tanto $\phi (A)$ es compacto.
Ejemplos
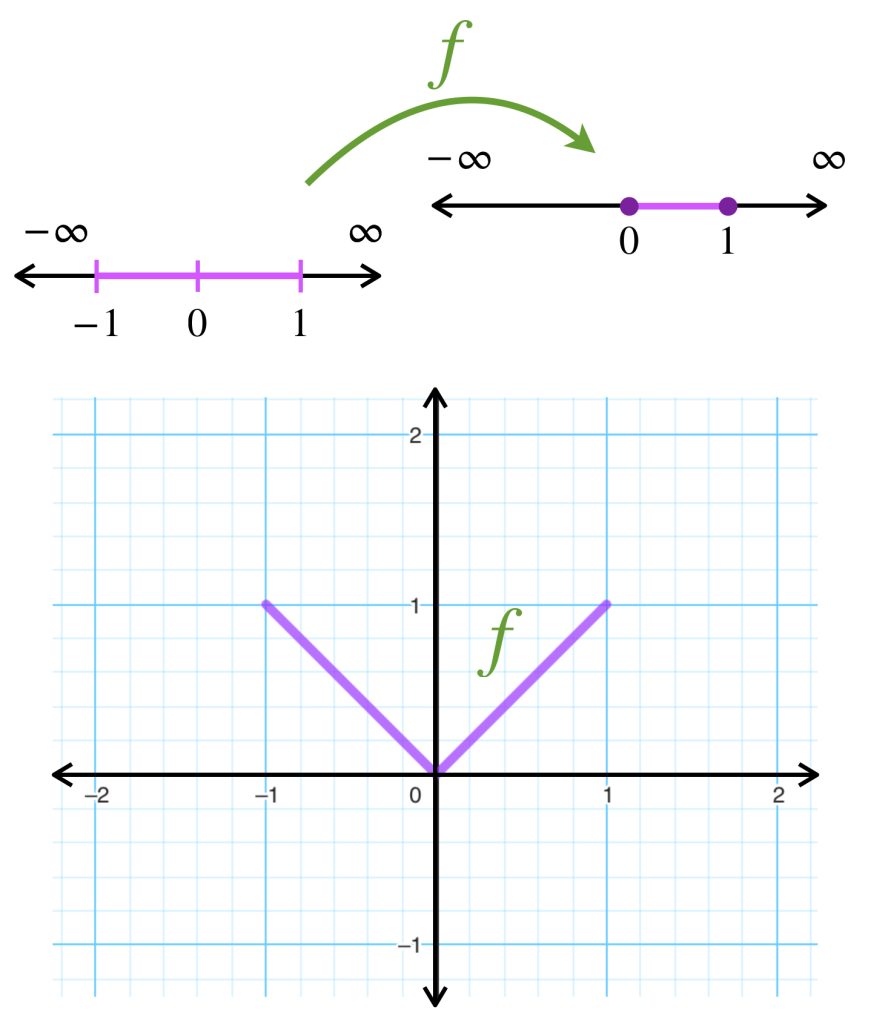
La función valor absoluto en un intervalo cerrado
Considera $\mathbb{R}$ con la métrica euclidiana y la función $f:[-1,1] \to \mathbb{R}$ donde $f(x)= |x|.$ Entonces $f$ es una función continua y $f([-1,1]) = [0,1]$ es compacto en $\mathbb{R}.$
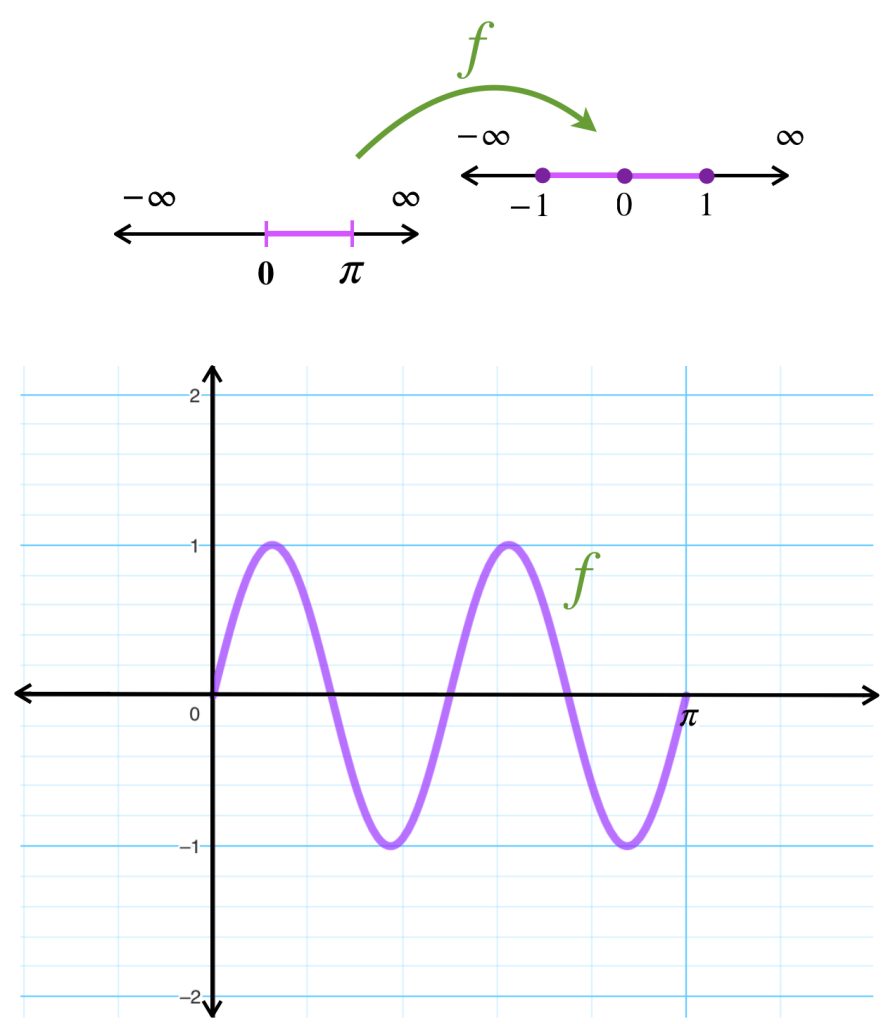
La función $sen(4x)$
Considera $\mathbb{R}$ con la métrica euclidiana y la función $f:[0, \pi ] \to \mathbb{R}$ donde $f(x)= sen(4x).$ Entonces $f$ es una función continua y $f([0, \pi]) = [-1,1]$ es compacto en $\mathbb{R}.$
La función $e^x$
Considera $\mathbb{R}$ con la métrica euclidiana y la función $f:[0, 2 ] \to \mathbb{R}$ donde $f(x)= e^x .$ Entonces $f$ es una función continua y $f([0, 2]) = [1,e^2]$ es compacto en $\mathbb{R}.$
Es resultado conocido que si $\phi: [0,1] \to \mathbb{R}$ es una función continua, entonces $\phi([0,1])= [a,b]$ donde $a = min \{f(x)|0 \leq x \leq 1 \} \, $ y $ \, b = max \{f(x)|0 \leq x \leq 1 \}.$ (Ver Teorema del máximo-mínimo). En efecto $[a,b]$ es un intervalo cerrado en $\mathbb{R}$ y por tanto es compacto.
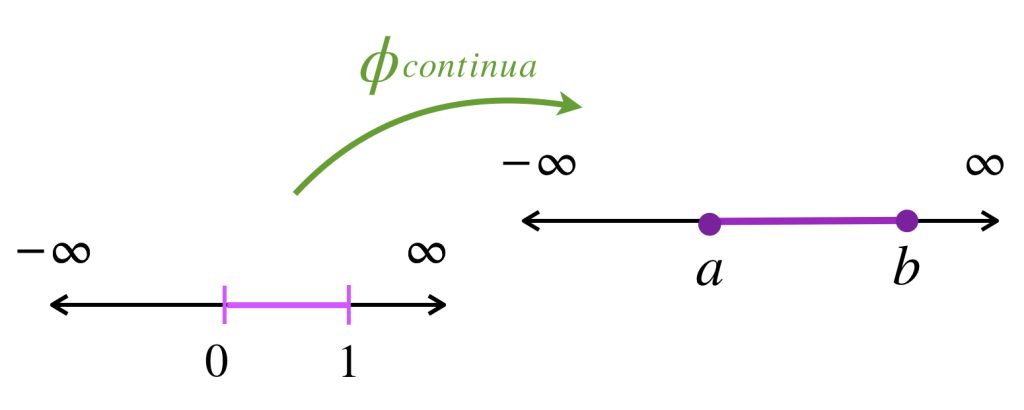
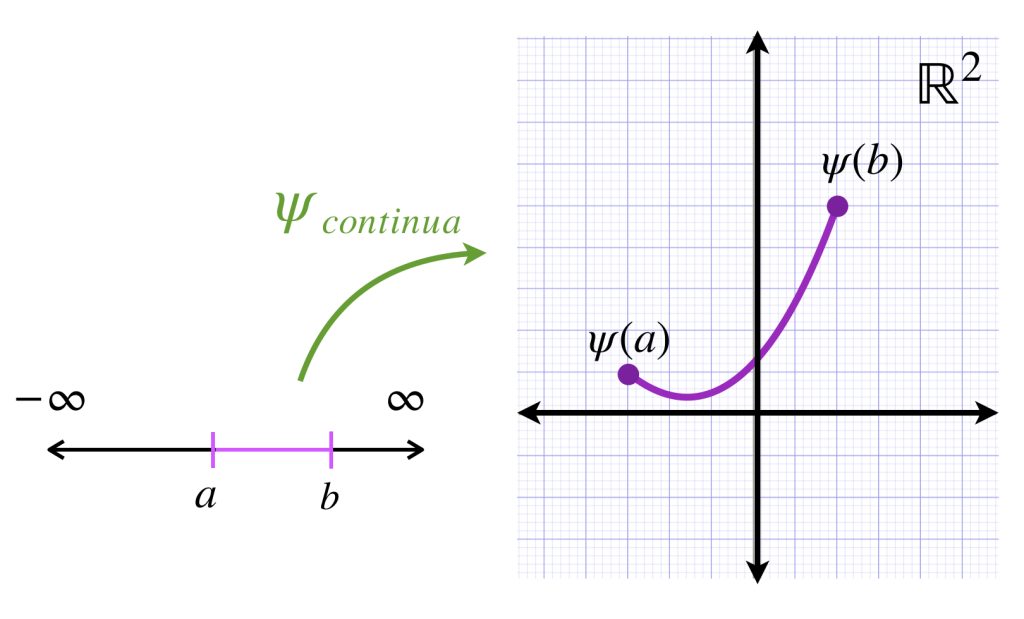
Bajo la misma idea podemos considerar a la función $\psi: \mathbb{R} \to \mathbb{R}^2$ dada por $\psi(t)=(t,\phi(t))$. Entonces, la curva de esta función es un conjunto compacto en $\mathbb{R}^2$
En la entrada anterior vimos que un conjunto compacto es cerrado y acotado. Podemos concluir el siguiente:
Corolario: Sea $A$ compacto. Entonces una función continua $\phi:A \subset X \to Y$ es acotada, pues la imagen bajo $\phi$ en el compacto es compacta y, por lo tanto, acotada. También podemos concluir que $\phi(A)$ es cerrada.
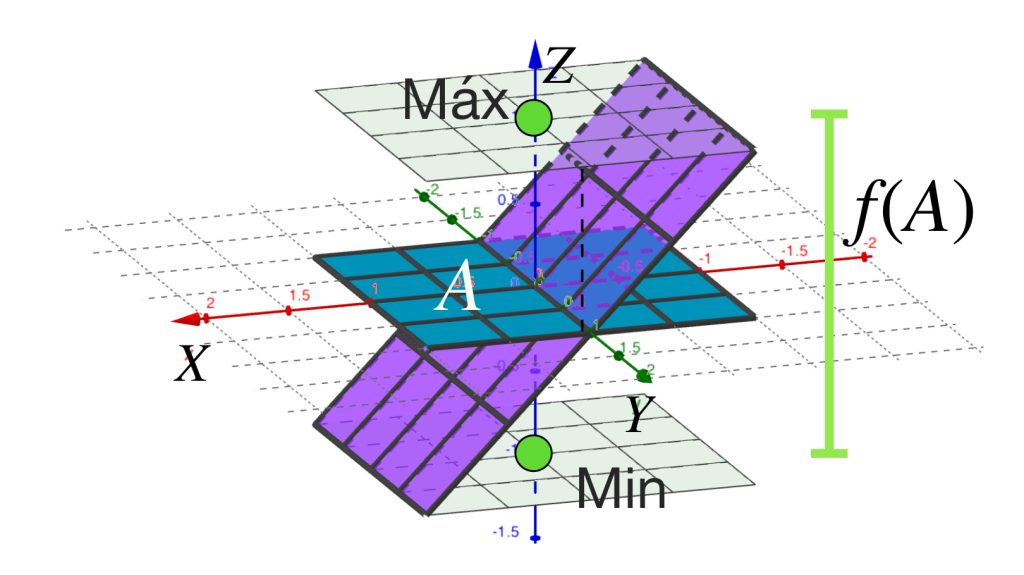
Este resultado nos permite delimitar una función en el espacio euclidiano de $\mathbb{R}$ con dos puntos importantes en el contradominio de la función: el máximo y el mínimo.
Probablemente este resultado te sea familiar de los cursos de cálculo:
Proposición: Sea $f:A\subset \mathbb{R}^n \to \mathbb{R}$ una función continua con $A$ cerrado y acotado (y por tanto compacto en $\mathbb{R}^n$). Entonces $f \,$ alcanza su mínimo y máximo en $A.$
En otros espacios métricos puede generalizarse como sigue:
Proposición: Sea $f:A \to \mathbb{R}$ una función continua con $A$ espacio métrico compacto y $\mathbb{R}$ con la métrica usual. Entonces $f$ alcanza su mínimo y máximo en $A$, es decir, existen puntos $x_1$ y $x_2$ en $A$ tales que para toda $x \in A$ se cumple que:
$$f(x_1) \leq x \leq f(x_2)$$
Demostración:
Si $A$ es compacto, la proposición anterior nos muestra que $f(A)$ es cerrado y acotado. Sea $m_0= inf\{f(x):x \in A\}$. Entonces $m_0 \in \overline{f(A)}$ y como $f(A)$ es cerrado, se concluye que $m_0 \in f(A)$, de modo que existe $x_1 \in A$ tal que $f(x_1)=m_0 \, $ por lo tanto $f$ alcanza su mínimo en $A$.
La demostración de que $f$ alcanza su máximo es análoga y se deja como ejercicio.
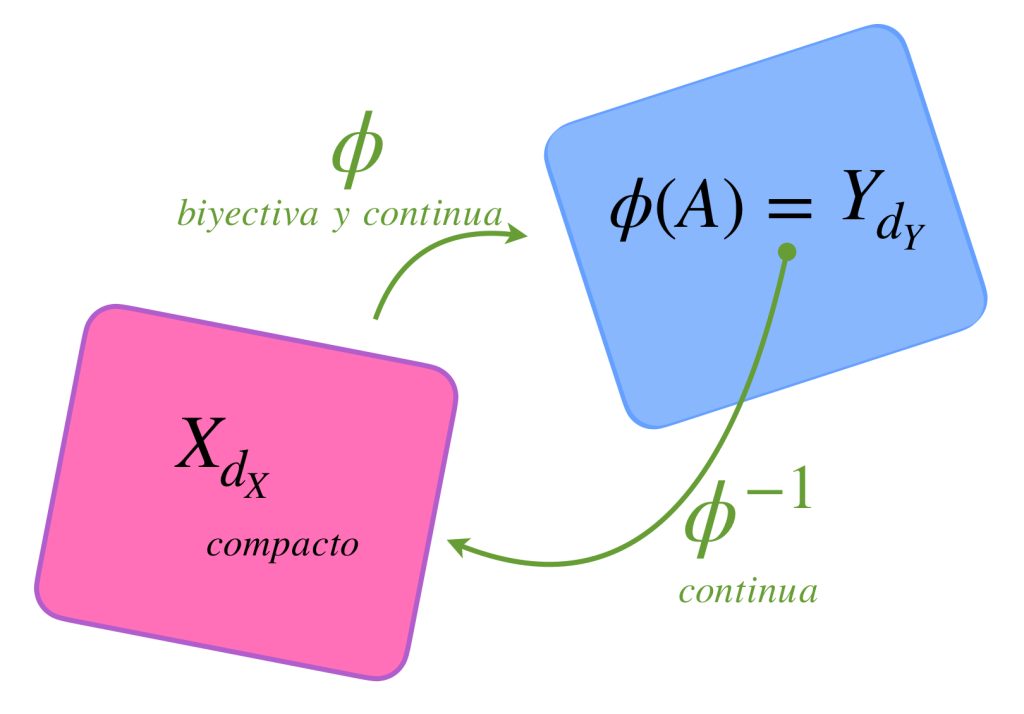
Proposición: Sean $(X,d_X)$ y $(Y,d_Y)$ espacios métricos con $X$ compacto y $\phi:X \to Y$ inyectiva y continua. Entonces existe la función inversa $\phi^{-1}$ en $\phi(X)$ y es continua en $\phi(X)$.
Demostración:
Para demostrar que $\phi^{-1}:\phi(X) \to X$ es una función continua, basta probar que la imagen inversa de esta función aplicada en conjuntos cerrados en $X$, es un conjunto cerrado en $Y$. Si $A$ es cerrado en $X$ entonces la imagen inversa respecto a la función $\phi^{-1}$ está dada por $\phi(A)$. Como $A$ es cerrado en un compacto entonces es compacto, de modo que $\phi(A)$ también es compacto y, por lo tanto, es cerrado en $Y$. Esto prueba que $\phi^{-1}$ es continua.
Finalizaremos esta entrada presentando un resultado que se deduce del anterior. La solución se propone como ejercicio al lector:
Proposición: Si $\phi:X \to Y$ es una función biyectiva y continua entre espacios métricos compactos, entonces es un homeomorfismo.
Más adelante…
Continuaremos visualizando aplicaciones de funciones continuas sobre conjuntos compactos, pero esta vez bajo una nueva definición: la continuidad uniforme.
Tarea moral
- Como parte de la prueba de la primera proposición, muestra que en efecto $\{\phi ^{-1}(A_i):i \in \mathcal{I}\}$ es una cubierta abierta de $A$.
- Argumenta la parte de la demostración de la primera proposición, en la que se afirma que si $A \subset \underset{1\leq j \leq m}{\bigcup}\phi ^{-1}(A_{i_j}),$ entonces $\{A_{i_1},A_{i_2},…,A_{i_m}\}$ es una subcubierta en $Y$ de $\mathcal{C}$ para $\phi (A)$.
- Prueba que si $f:A \to \mathbb{R}$ es una función continua con $A \subset \mathbb{R}^n$ cerrado y acotado, entonces $f$ alcanza su máximo en $A.$
- Prueba que si $X$ y $Y$ son homeomorfos, entonces $X$ es compacto si y solo si $Y$ es compacto.
- Demuestra que si $\phi:X \to Y$ es una función biyectiva y continua entre espacios métricos compactos, entonces es un homeomorfismo.