[latexpage]
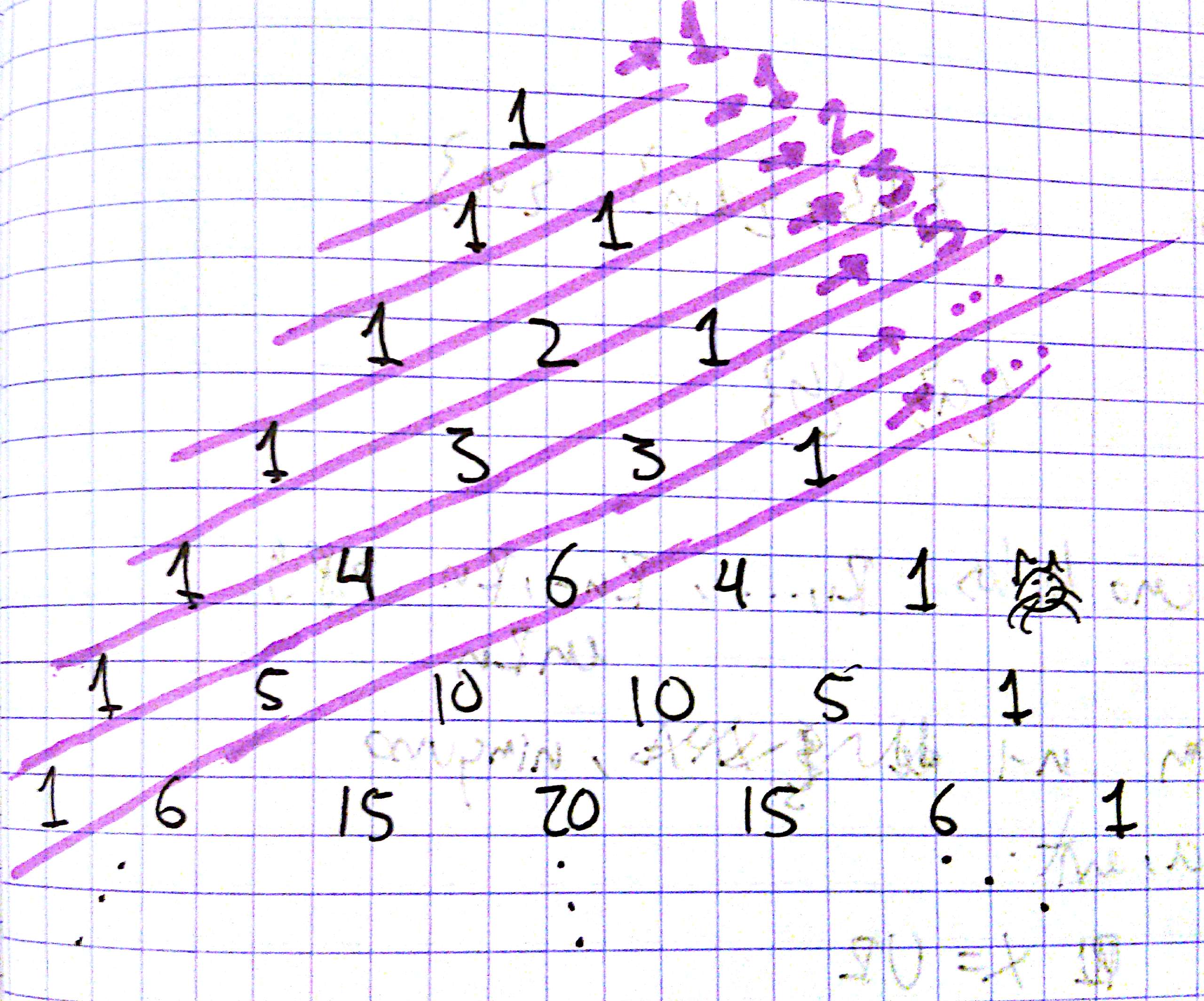
En esta entrada quiero dar dos demostraciones de un hecho sensacional: si se suman los números que están en las diagonales del triángulo de Pascal, entonces se van obteniendo los números de Fibonacci. Esto se ve más claro en la siguiente imagen. Cada diagonal es lo que está entre dos líneas rosas (¿moradas?). Arriba a la derecha están las sumas.
Este dato curioso lo acabo de mandar a la página de FB Art of Mathematics. A quien maneja la página le gustó e hizo una imagen más bonita que puedes ver dando clic al nombre de la página.
Originalmente, me contaron de esta propiedad cuando tomaba entrenamientos de Olimpiada de Mate en el DF. La Prueba 1 de abajo fue la que se dio en el entrenamiento: usar inducción y la regla para formar el triángulo de Pascal. Sin embargo, el problema me gustó tanto que busqué una prueba alternativa. Esa es la Prueba 2 que pongo a continuación. Esa es mi favorita por que simplemente hay que contar algo de dos maneras distintas y el resultado sale inmediatamente.
La Prueba 2 forma parte de una colección más grande de pruebas de doble conteo que publiqué en Tzaloa (la revista de la Olimpiada Mexicana de Matemáticas). Pueden ver la revista en línea en este enlace: Tzaloa 2011-3
Prueba 1
Vamos a proceder por inducción fuerte. En la primera y segunda diagonal claramente tenemos $1$ y $1$, que son los primeros números de Fibonacci, $F_1$ y $F_2$.
Supongamos que el enunciado se cumple para $n-2$ y $n-1$, y vamos a la $n$-ésima diagonal ($n\geq 2$). Hasta la izquierda de la $n$-ésima diagonal hay un $1$. Ignorémoslo un momento. Notemos que todos los demás números están formados por la suma de un número de la $n-2$-ésima diagonal y uno de la $n-1$-ésima. De hecho, usamos todos los números de estas diagonales, a excepción del $1$ hasta la izquerda de la $n-1$-ésima diagonal. Pero este se compensa con el $1$ que habíamos ignorado.
De esta forma, la suma de los números en la $n$-ésima diagonal es igual a la suma de los de la $n-1$-ésima y la $n-2$-ésima. Por hipótesis inductiva, esto es $F_{n-1}+F_{n-2}$, que por la regla de Fibonacci es $F_n$. Esto termina la demostración.
Prueba 2
Esta prueba se basa en el principio de doble conteo. El principio de doble conteo dice algo sencillo, pero con aplicaciones muy versátiles:
«Si tengo una pregunta combinatoria que resuelvo de dos formas distintas y correctas, y de una forma cuento que son $A$ elementos y de la otra $B$, entonces $A=B$.»
Nuestra pregunta auxiliar será la siguiente:
Consideremos un tablero de $1\times n$ cuadrados. Pongamos una moneda en la casilla de hasta la izquierda. ¿De cuántas formas podemos llevar la moneda a la casilla de hasta la derecha si se permiten dar pasos a la derecha de $1$ o $2$ cuadrados? Llamemos a este número $G_n$
Veamos algunos valores pequeños. Para $n=1$ hay una forma (no hacer nada). Para $n=2$ también sólo hay una forma (dar un paso de $1$). Para $n=3$ podemos dar dos pasos de $1$, o bien uno de $2$. Estos valores coinciden con los números de Fibonacci $G_1=F_1$, $G_2=F_2$ y $G_3=F_3$.
De hecho, siempre salen números de Fibonacci. Esto se debe a que si el primer paso es de $1$, entonces hay $G_{n-1}$ formas de terminar, y si el primer paso es de $2$, entonces hay $G_{n-2}$ formas de terminar. Entonces $G_n$ tiene la misma recursión que Fibonacci y coincide en sus primeros dos términos, así que una prueba inductiva estándar da que $F_n=G_n$.
Vamos a contar $G_n$ de otra forma. Primero preguntémonos, ¿cuántos pasos de dos queremos dar? Supongamos que queremos $k$. Entonces en total hacemos $n-1-k$ pasos ($k$ de $2$ y $n-1-2k$ de $1$). Todavía tenemos que decidir en cuáles de los $n-1-k$ pasos vamos a hacer pasos de $2$. Esto se puede hacer de $\binom{n-1-k}{k}$ formas.
Finalmente, observemos que $k$ puede tomar cualquier valor de $0$ a $\left\lfloor\frac{n-1}{2}\right\rfloor$. De esta forma, y usando el principio de doble conteo:
$$F_n=G_n=\sum_{k=0}^{\left\lfloor\frac{n-1}{2}\right\rfloor} \binom{n-1-k}{k}$$.
Notemos que a la derecha tenemos precisamente los números del triángulo de Pascal en la $n$-ésima diagonal. Esto termina la demostración.