$\mathit{\text{MATERIAL EN REVISIÓN}}$

Introducción

En la entrada anterior link aprendimos que es posible acercarnos a funciones continuas que tienen su dominio en un intervalo cerrado en $\mathbb{R}.$ En esta sección probaremos que esta idea puede generalizarse en funciones cuyo dominio es un espacio métrico compacto. Presentamos el teorema y la demostración de dos lemas que usaremos para probarlo.

Teorema. Stone-Weierstrass: Sea $K$ un espacio métrico compacto. Sea $A\subset {\mathcal{C}}^0(K,\mathbb{R}),$ es decir, $A$ es un conjunto de funciones continuas de $K$ en $\mathbb{R}.$ Si $A$ satisface las siguientes propiedades:

a) Para cada $\lambda ,\mu \in \mathbb{R}$ y $f,g\in A$ se cumple que $$\lambda f+\mu g\in A.$$ Esto es, $A$ es cerrado bajo combinaciones lineales.

b) Para cada $f,g\in A$ se cumple que $$f\cdot g\in A.$$ Esto es, $A$ es cerrado bajo producto de funciones.

c) $1\in A,$ donde $1$ es la función constante que para cada $x\in K$ asigna el valor $1.$

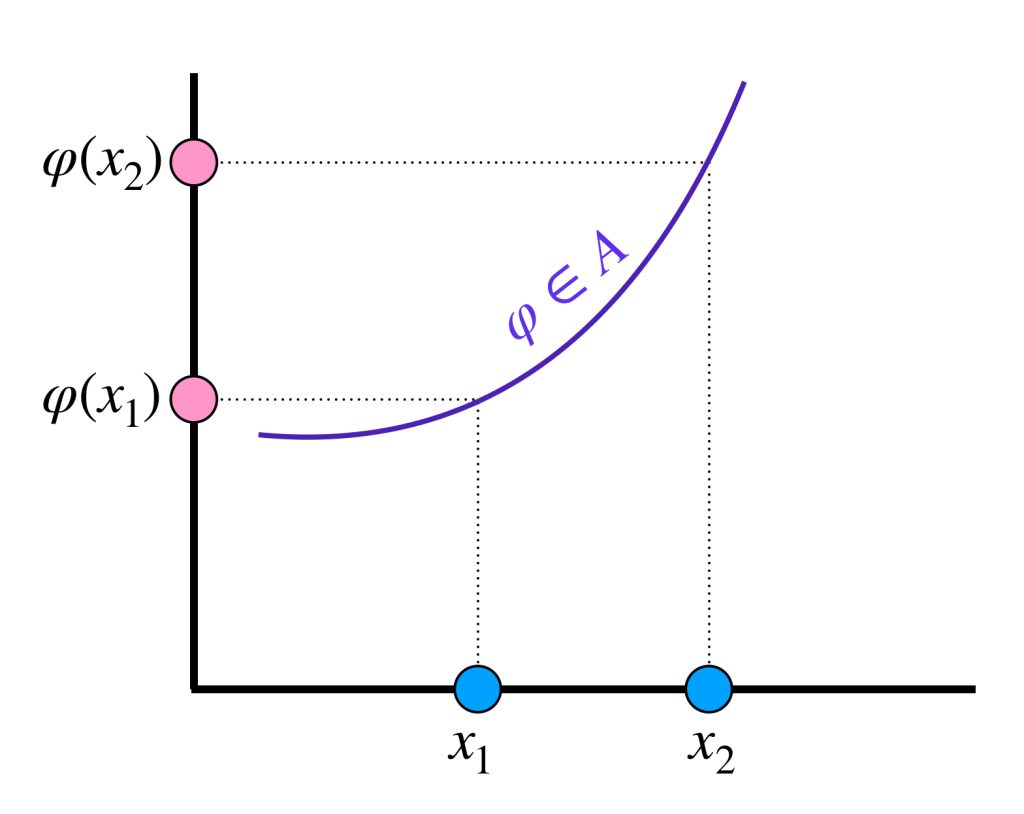
d) Para cualesquiera $x_1,x_2\in K$ tales que $x_1\ne x_2$ existe una función $\phi \in A$ tal que $\phi (x_1)\ne \phi (x_2).$

Entonces $A$ es denso en ${\mathcal{C}}^0(K,\mathbb{R}),$ es decir, $\bar{A}={\mathcal{C}}^0(K,\mathbb{R}).$

Nota que esto significa que toda función continua $f:K\to \mathbb{R}$ está en la cerradura de $A$ y por lo visto en la entrada Convergencia, tenemos que $f$ puede aproximarse con funciones en $A$ según la métrica uniforme $d_{\mathrm{\infty }}.$

La demostración de este teorema se hará a través de cuatro lemas. En el primero garantizaremos la existencia de una función que tome dos valores específicos en dos puntos específicos.

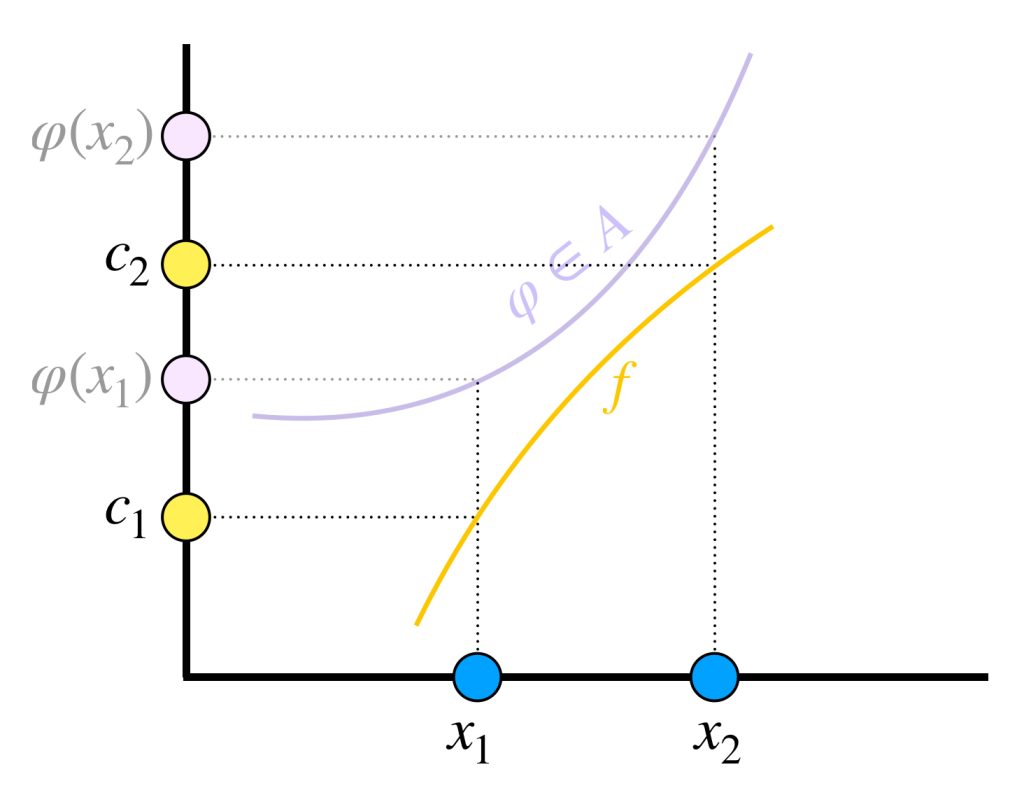
Lema 1: Sean $K$ y $A$ como en las hipótesis del teorema. Dados $x_1\ne x_2\in K$ y $c_1,c_2\in \mathbb{R}$ existe $f\in A$ tal que $f(x_1)=c_1$ y $f(x_2)=c_2.$

Demostración:
De acuerdo con el inciso d), existe $\phi \in A$ tal que $\phi (x_1)\ne \phi (x_2).$

Sin embargo buscamos $f$ que en $x_1$ vale específicamente $c_1$ y en $x_2$ vale $c_2.$

Veamos si dicha $f$ puede obtenerse como combinación lineal de $\phi$ y la función constante $1,$ es decir que $f(x)=\lambda \phi (x)+\mu 1$ para algunos $\lambda ,\mu \in \mathbb{R}.$

Encontrar $\lambda$ y $\mu$ que satisfacen lo deseado equivale a resolver el sistema de ecuaciones

$$\{\begin{array}{ll}\lambda \phi (x_1)+\mu & =c_1\\ \lambda \phi (x_2)+\mu & =c_2\end{array}$$

Según las fórmulas de Cramer para sistemas cuadrados, que pueden consultarse en Álgebra Lineal I: Determinantes en sistemas de ecuaciones lineales y regla de Cramer la solución existe y es única si y solo sí el determinante de la matriz de coeficientes dada por

$$\left|\begin{array}{cc}\phi (x_1)& 1\\ \phi (x_2)& 1\end{array}\right|$$

satisface:

$$\left|\begin{array}{cc}\phi (x_1)& 1\\ \phi (x_2)& 1\end{array}\right|=\phi (x_1)–\phi (x_2)\ne 0$$

Lo cual sí ocurre, pues $\phi (x_1)\ne \phi (x_2)\Rightarrow \phi (x_1)–\phi (x_2)\ne 0.$

Por lo tanto existe la solución única al sistema de ecuaciones y así existe $f\in A$ con $f(x)=\lambda \phi (x)+\mu$ tal que $f(x_1)=c_1$ y $f(x_2)=c_2.$

Lema 2: Si $A\subset {\mathcal{C}}^0(K,\mathbb{R})$ es tal que tiene las propiedades a), b), c) del teorema, entonces $\bar{A}$ también las tiene.

Demostración:
a) Sean $\lambda ,\mu \in \mathbb{R}$ y $\phi ,\gamma \in \bar{A},$ queremos probar que $\lambda \phi +\mu \gamma$ también está en $\bar{A}.$

Como $\phi \in \bar{A}$ entonces, por lo visto en Convergencia sabemos que existe una sucesión $(f_n{)}_{n\in \mathbb{N}}$ de elementos de $A$ tales que $f_n\to \phi ,$ es decir

$$\begin{array}{}\text{(1)}& \underset{n\to \mathrm{\infty }}{lim}{f}_n=\phi .\end{array}$$

De igual manera existe una sucesión $(g_n{)}_{n\in \mathbb{N}}$ de elementos de $A$ tales que $g_n\to \gamma ,$ es decir

$$\begin{array}{}\text{(2)}& \underset{n\to \mathrm{\infty }}{lim}{g}_n=\gamma .\end{array}$$

Ya que para cada $n\in \mathbb{N}$ se cumple que $\lambda f_n+\mu g_n\in A.$ Si demostramos que la sucesión $(\lambda f_n+\mu g_n{)}_{n\in \mathbb{N}}$ converge a $\lambda \phi +\mu \gamma$ esto probaría que $\lambda \phi +\mu \gamma \in \bar{A}.$ Probemos que $d_{\mathrm{\infty }}(\lambda f_n+\mu g_n,\lambda \phi +\mu \gamma )=0.$ Sea $\epsilon >0.$ Por 1) y 2) sabemos que existen $N_1$ y $N_2\in \mathbb{N}$ tales que para cada $n\ge N_1,$

$$d_{\mathrm{\infty }}(f_n,\phi )<\frac{\epsilon }{2|\lambda |}$$

Y así

$$\begin{array}{r}|\lambda |d_{\mathrm{\infty }}(f_n,\phi )<\frac{\epsilon }{2}\end{array}$$

Y para cada $n\ge N_2,$

$$d_{\mathrm{\infty }}(g_n,\gamma )<\frac{\epsilon }{2|\mu |}$$

Y así

$$\begin{array}{r}|\mu |d_{\mathrm{\infty }}(g_n,\gamma )<\frac{\epsilon }{2}.\end{array}$$

Entonces para cada $n\ge \text{máx}\{N_1,N_2\}$ y para cada $x\in K$ tenemos:
$$\begin{array}{rl}d(\lambda f_n(x)+\mu g_n(x),\lambda \phi (x)+\mu \gamma (x))& =|\lambda f_n(x)+\mu g_n(x)–\lambda \phi (x)–\mu \gamma (x)|\\ & =|\lambda f_n(x)–\lambda \phi (x)+\mu g_n(x)–\mu \gamma (x)|\\ & \le |\lambda f_n(x)–\lambda \phi (x)|+|\mu g_n(x)–\mu \gamma (x)|\\ & =|\lambda ||f_n(x)–\phi (x)|+|\mu ||g_n(x)–\gamma (x)|\\ & \le |\lambda |d_{\mathrm{\infty }}(f_n,f)+|\mu |d_{\mathrm{\infty }}(g_n,\gamma )\\ & <\frac{\epsilon }{2}+\frac{\epsilon }{2}\\ & =\epsilon .\end{array}$$

Por lo tanto $d_{\mathrm{\infty }}(\lambda f_n+\mu g_n,\lambda \phi +\mu \gamma )=0$ y así $(\lambda f_n+\mu g_n{)}_{n\in \mathbb{N}}\to \lambda \phi +\mu \gamma$ lo que demuestra que $\lambda \phi +\mu \gamma \in \bar{A}.$

b) Buscamos demostrar que para cualesquiera $\phi ,\gamma \in \bar{A}$ también se cumple que $\phi \cdot \gamma \in \bar{A}.$

Ya que para cada $n\in \mathbb{N}$ se cumple que $f_n\cdot g_n\in A.$ Si demostramos que la sucesión $(f_n\cdot g_n{)}_{n\in \mathbb{N}}$ converge a $\phi \cdot \gamma$ esto probaría que $\phi \cdot \gamma \in \bar{A}.$

Probemos entonces que $\underset{n\to \mathrm{\infty }}{lim}{d}_{\mathrm{\infty }}(f_n\cdot g_n,\phi \cdot \gamma )=0.$ Esto se logrará si conseguimos acotar el valor de $d(f_n(x)\cdot g_n(x),\phi (x)\cdot \gamma (x))\in \mathbb{R}$ para cada $x\in K.$

Dado que $\phi ,\gamma$ son continuas en un compacto, concluimos que son acotadas en el dominio. Así existen reales mayores que cero $M_1$ y $M_2$ tales que para cada $x\in K:$

$$\begin{array}{}\text{(3)}& |\phi (x)|& \le M_1\text{ y }\text{(4)}& |\gamma (x)|& \le M_2.\end{array}$$

Por otro lado, como $\underset{n\to \mathrm{\infty }}{lim}{g}_n=\gamma ,$ existe $N_3\in \mathbb{N}$ tal que para cada $n\ge N_3,|g_n(x)–\gamma (x)|\le 1.$ Entonces

$$\begin{array}{rlrlrlrl}& & -1& \le & & g_n(x)–\gamma (x)& & \le 1\\ & \Rightarrow & -1+\gamma (x)& \le & & g_n(x)& & \le 1+\gamma (x)\\ & \Rightarrow & -1-M_2\le -1+\gamma (x)& \le & & g_n(x)& & \le 1+\gamma (x)\le 1+M_2\end{array}$$

Por lo tanto si $n\ge N_3,$

$$\begin{array}{}\text{(5)}& |g_n(x)|\le M_2+1.\end{array}$$

Además, por 1) y 2) sabemos que para cada $\epsilon >0$ existen $N_4$ y $N_5\in \mathbb{N}$ tal que para cada $n\ge N_4$

$$d_{\mathrm{\infty }}(f_n,\phi )<\frac{\epsilon }{2(M_2+1)},$$

y para $n\ge N_5,$

$$d_{\mathrm{\infty }}(g_n,\gamma )<\frac{\epsilon }{2M_1}.$$

De lo anterior se sigue que para cada $n\ge \text{máx}\{N_3,N_4,N_5\}$

$$\begin{array}{rl}|f_n(x)\cdot g_n(x)–\phi (x)\cdot \gamma (x)|& =|f_n(x)\cdot g_n(x)-\phi (x)\cdot g_n(x)+\phi (x)\cdot g_n(x)-\phi (x)\cdot \gamma (x)|\\ & \le |f_n(x)\cdot g_n(x)–\phi (x)\cdot g_n(x)|+|\phi (x)\cdot g_n(x)-\phi (x)\cdot \gamma (x)|\\ & =|g_n(x)|\cdot |f_n(x)–\phi (x)|+|\phi (x)|\cdot |g_n(x)-\gamma (x)|\\ & \le (M_2+1)|f_n(x)–\phi (x)|+M_1|g_n(x)-\gamma (x)|\\ & <(M_2+1)\frac{\epsilon }{2(M_2+1)}+M_1\frac{\epsilon }{2M_1}\\ & =\epsilon \end{array}$$

Por lo tanto $\underset{n\to \mathrm{\infty }}{lim}{d}_{\mathrm{\infty }}(f_n\cdot g_n,\phi \cdot \gamma )=0$ y así $(f_n\cdot g_n{)}_{n\in \mathbb{N}}\to \phi \cdot \gamma$ lo que demuestra que $\phi \cdot \gamma \in \bar{A}.$

c) Dado que la función $1\in A$ se sigue que $1\in \bar{A}$ pues $A\subset \bar{A}.$

Más adelante…

Veremos dos lemas más que necesitamos en la demostración del teorema de Stone-Weierstrass. Por el momento sugerimos trabajar con los siguientes ejercicios para desarrollar más la idea de densidad.

Tarea moral

1. Sea $X$ un espacio métrico y sean $Z$ y $Y$ tales que $Z\subset Y\subset X$ y $Z$ es denso en $X.$ Demuestra que $Y$ es denso en $X.$
2. Sea $\varphi :X\to Y$ continua y suprayectiva. Demuestra que si $A$ es denso en $X,$ entonces $\varphi (A)$ es denso en $Y.$
3. Antes dos definiciones:
   Un conjunto $A$ es a lo más numerable si existe una función inyectiva $f:A\to \mathbb{N}.$
   Un espacio métrico es separable si contiene un subconjunto que es a lo más numerable y denso en $X.$
   Demuestra que todo espacio métrico compacto es separable. Se recomienda tomar un conjunto finito de bolas de radio $\frac{1}{k}$ para cada $k\in \mathbb{N}$ cuya unión es $X.$

Enlaces

• Análisis Matemático.
• Enlace a entrada anterior.
• Enlace a entrada siguiente.