Introducción

Si queremos construir una noción más general de integración, un requisito mínimo es que se debe ajustar a la idea intuitiva de que la integral (al menos en $\mathbb{R}$) es el «área bajon la curva» de una función. Es entonces natural pensar en que primero hay que definir de manera precisa y lo más general posible conceptos como longitud, área, volúmen, y sus análogos en dimensiones más altas. Ésta es precisamente la idea de medida en $\mathbb{R}^n$. Más adelante construiremos la integral de Lebesgue sobre este concepto.

Idealmente, nos gustaría asignarle a cada subconjunto $A\subseteq \mathbb{R}^n$ algún número no negativo $\lambda (A)$ (su medida en $\mathbb{R}^n$). Para que ésta noción tenga sentido, debería satisfacer ciertas propiedades «intuitivas» y a las que ya estamos acostumbrados en dimensiones bajas. Las siguientes son deseables:

• Monotonía. Si $A\subseteq B$ son subconjuntos de $\mathbb{R}^n$, entonces $\lambda(A)\leq \lambda(B)$. Pues $B$ es «más grande» que $A$.
• Aditividad. Si $A\cap B=\emptyset$ son subconjuntos ajenos, entónces $\lambda(A\cup B)=\lambda(A)+\lambda(B)$.
• Normalización. La medida de un rectángulo generalizado, es decir un producto de intervalos $\prod_{i=1}^{n}[a_i,b_i]\subseteq\mathbb{R}^n$, debería ser el producto de las longitudes de sus lados: $\prod_{i=1}^{n}(b_i-a_i)$. Ésta idea coincide con el cálculo elemental de áreas de rectángulos y volúmenes de prismas rectangulares.

Podemos usar las ideas anteriores como punto de partida para intentar definir la medida de conjuntos más generales. El camino que seguiremos es: Tomar a los rectángulos como «unidades de medida» (simulando el punto 3) y buscar la mejor forma de aproximar un conjunto «por fuera» mediante rectángulos.

Rectángulos y su volumen.

Definición. Por intervalos (acotados) nos referimos a conjuntos no vacíos de $\mathbb{R}$ de la forma $[a,b]:=\{x\in \mathbb{R} \ : \ a\leq x \leq b \}$; $[a,b):=\{x\in \mathbb{R} \ : \ a\leq x < b \}$; $(a,b]:=\{x\in \mathbb{R} \ : \ a< x \leq b \}$; $(a,b):=\{x\in \mathbb{R} \ : \ a< x < b \}$, donde $a\leq b$ son números reales. Llamaremos a los intervalos de la forma $[a,b]$ como intervalos cerrados y a los de la forma $(a,b)$ como intervalos abiertos. Definimos la longitud $|I|$ de un intervalo $I=[a,b],[a,b),(a,b],(a,b)$ como $$|I|=b-a.$$ La longitud de un intervalo puede ser 0. A los intervalos de longitud 0 (i.e. que constan de un sólo elemento) los llamaremos «degenerados«.

Para esta parte, trabajaremos casi exclusivamente con intervalos cerrados o abiertos y acotados. Por brevedad nos referiremos a estos simplemente como intervalos.

Definición. Un rectángulo cerrado (abierto) en $\mathbb{R}^n$ es un producto cartesiano $$R:=I_1\times\ I_2\times \dots \times I_n.$$ Donde $I_1,I_2,\dots, I_n$ son intervalos cerrados (abiertos). Definimos el volúmen del rectángulo $R=I_1\times\ I_2\times \dots \times I_n$ como $$|R|=\prod_{k=1}^{n}|I_k|.$$ Si alguno de los intervalos componente de un rectángulo es degenerado, diremos también que el rectángulo es «degenerado».

Observaciones.

• Para cualquier rectángulo $R$, su volumen es no negativo (posiblemente 0) y finito: $0\leq |R| < \infty$. Un rectángulo tiene volúmen 0 si y sólo si es degenerado.
• Los intervalos cerrados/abiertos son rectángulos en $\mathbb{R}$. En este caso su volumen coincide con su longitud.
• Si $R\subseteq Q$ son rectángulos, entónces $|R|\leq |Q|$. Pues la única posibilidad es que al descomponer $R$ y $Q$ como producto de intervalos, cada intervalo en la descomposición de $R$ sea un subintervalo del correspondiente a $Q$ y la monotonía es inmediata en el caso de intervalos.
• La cerradura de un rectángulo $R$ es un rectángulo cerrado $\overline{R}$. Además $|R|=|\overline{R}|$.
• Los rectángulos cerrados son subconjuntos cerrados y acotados en $\mathbb{R}^n$ (por ende compactos). Los rectángulos abiertos son subconjuntos abiertos de $\mathbb{R}^n$. La cerradura de un rectángulo abierto es un rectángulo cerrado del mismo volúmen.
• El volúmen de un rectángulo, coincide con la noción de «medida» que nos da la integral de Riemann, a saber, la medida de Jordan: $J(R)=\int \chi_R = |R|$, donde $\int$ denota la integral de Riemann sobre algún rectángulo cerrado y no degenerado que contenga a $R$ y $\chi_R$ es la función característica de $R$.

Las siguientes propiedades del volúmen de los rectángulos nos serán útiles más adelante.

Proposición. (Aproximación por rectángulos abiertos y cerrados). Si $R$ es un rectángulo cerrado, entónces $$|R|=\inf \{|Q| \ :\ R\subseteq Q \text{ y $Q$ es un rectángulo abierto} \}.$$ Similarmente Si $R$ es abierto, entónces $$|R|=\sup \{|Q| \ :\ Q\subseteq R \text{ y $Q$ es un rectángulo cerrado}\ \}.$$

Demostración. Para el caso en el que $R=[a_1,b_1]\times [a_2,b_2]\times \dots \times [a_n,b_n]$ es cerrado, de las observaciones sabemos que $|R|\leq |Q|$ para cualquier rectángulo abierto tal que $R\subseteq Q$, de donde $$|R|\leq \inf\{|Q| :\ R\subseteq Q \text{ y $Q$ es un rectángulo abierto} \} .$$

Por otro lado, al definir el rectángulo abierto $$Q_{\varepsilon}=(a_1- \varepsilon,a_1+ \varepsilon ) \times (a_2-\varepsilon,a_2+\varepsilon)\times \dots \times (a_n-\varepsilon,a_n+\varepsilon)$$

Es claro que $R\subseteq Q_{\varepsilon}$ para todo $\varepsilon>0$. Usando la definición, $|Q_{\varepsilon}|$ se puede escribir como $$\prod_{k=1}^{n}(b_k-a_k)+\varepsilon f(\varepsilon)=|R|+\varepsilon f(\varepsilon)$$ Donde $f(\varepsilon)$ es algún polinomio en $\varepsilon$. Por continuidad se sigue que $\lim_{\varepsilon \to 0^+}|Q_{\varepsilon}|=|R|$. Concluimos $$|R|\geq \inf \{|Q| \ :\ R\subseteq Q \text{ y $Q$ es un rectángulo abierto} \}.$$ El argumento para rectángulos abiertos es similar.

$\square$

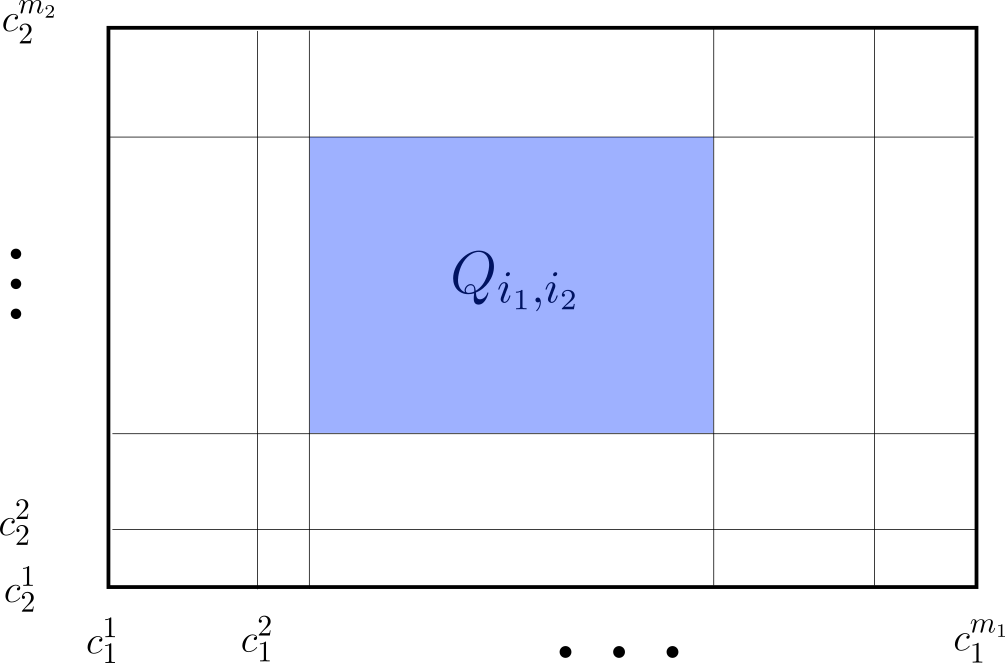
Proposición (Descomposición en subrectángulos preserva volúmen). Sea $R=[a_1,b_1]\times [a_2,b_2]\times \dots \times [a_n,b_n]$ un rectángulo cerrado y no degenerado. Supongamos que para cada $i=1,2,\dots ,n$ $$a_i=c_i^1<c_i^2<\dots <c_i^{m_i}=b_i.$$ Son puntos intermedios del intervalo $[a_i,b_i]$. Esto induce una descomposición de $R$ en subrectángulos: $$Q_{i_1,i_2,\dots, i_n}=[c_1^{i_1},c_1^{i_1+1}]\times [c_2^{i_2},c_2^{i_2+1}]\times \dots \times [c_n^{i_n},c_n^{i_n+1}].$$ Con $1\leq i_1 < m_1,1\leq i_2 < m_2, \dots ,1\leq i_n < m_n $. Entonces:
$$|R|=\sum_{i_1,i_2,\dots, i_n} |Q_{i_1,i_2,\dots, i_n}|.$$

Demostración. Denotemos por $J$ a las $n$-tuplas de la forma $(i_1,i_2,\dots, i_n)$ con $1\leq i_1 < m_1,1\leq i_2 < m_2, \dots 1\leq i_n < m_n $. Si definimos $d_k^j=(c_k^{j+1}-c_k^j)$ (los lados de los subrectangulos), tenemos que $(a_k-b_k)=\sum_{j=1}^{m_{i}-1} d_k^j$. Luego, lo anterior se reduce a probar:
$$\prod_{k=1}^{n}(b_k-a_k)=\prod_{k=1}^{n}\sum_{j=1}^{m_i-1}(d_k^j)=\sum_J \prod_{k=1}^{n}(d_k^{i_k}).$$

La ultima igualdad es inmediata por distributividad. (Para convencerte de esto, piensa que para desarrollar el producto de en medio, para cada $k$ hay que escoger un término $j=i_k$, multiplicar estos términos para obtener $d_1^{i_1}d_2^{i_2}\dots d_n^{i_n}$ y luego sumar sobre todas las posibles elecciones, que es precisamente el término derecho ).

$\square$

Proposición. Si $R$ es un rectángulo cerrado cubierto por una cantidad finita $N$ de rectángulos (cerrados o abiertos) no degenerados: $R\subseteq \bigcup_{k=1}^{N} Q_k$, entonces $$|R|\leq \sum_{k=1}^{N} |Q_k|.$$

Demostración. Tomando las cerraduras de $Q_1,Q_2,\dots, Q_N$ es suficiente probarlo cuando la cubierta consta de rectángulos cerrados. Al ser una cantidad finita de rectángulos, podemos encontrar un rectángulo $P$ suficientemente grande que contenga a $R,Q_1,Q_2,\dots, Q_N$. Proyectemos los extremos de los intervalos componente de cada uno de los rectángulos $R,Q_1,Q_2,\dots, Q_N$ sobre los intervalos componente de $P$. Por construcción, esto induce descomposiciones en subrectángulos en cada uno de $P,R,Q_1,Q_2,\dots, Q_n$ (observa la figura). Denotemos todos los subrectángulos (de $P$) como $S_1,S_2,\dots, S_M$. Como $R\subseteq \bigcup_{k=1}^{N} Q_k$, cada subrectángulo $S$ de $R$ debe ser también un subrectángulo de algún $Q_k$. Luego, por la proposición anterior:
$$|R|=\sum_{S_j\subseteq R} |S_j|\leq \sum_{k=1}^{N} \sum_{S_j\subseteq Q_k} |S_j|=\sum_{k=1}^{N}|Q_k|.$$

$\square$

Proposición (Invarianza bajo traslaciones). Si $R=I_1\times I_2\times \dots \times I_n$ es un rectángulo, entonces la traslación por $v=(v_1,v_2,\dots, v_n)\in \mathbb{R}^n$, $v+R$ es un rectángulo con el mismo volumen que $R$ (Donde definimos la traslación por el vector $x\in \mathbb{R}^n$ de un conjunto $B$ como $x+B=\{x+b\ : \ b\in B \}$).

Demostración. Lo anterior se cumple para intervalos abiertos/cerrados, por ejemplo si $x\in \mathbb{R}$, $x+[a,b]=[a+x,b+x]$ y $|I|=(b-a)=((b+x)-(a-x))=|x+I|$. El otro caso es similar.

Para el caso de rectángulos, es fácil ver que $v+R=(v_1+I_1)\times (v_2+I_2)\times \dots \times (v_n+I_n)$. De donde por el caso anterior: $$|R|=\prod_{k=1}^{n}|I_k|=\prod_{k=1}^{n}|v_k+I_k|=|v+R|.$$

$\square$

Proposición (Dilataciones). Si $R=I_1\times I_2\times \dots \times I_n$ es un rectángulo, entonces la dilatación $cR$ es un rectángulo con $$|cR|=|c|^n|R|. $$ (Donde definimos la dilatación por $c\in \mathbb{R}$ de un conjunto $B$ como $cB=\{cb\ : \ b\in B \}$).

Demostración. Sin pérdida de generalidad, supongamos que $R=[a_1,b_1]\times \dots \times [a_n,b_n]$ es un rectángulo cerrado. Si $c\geq 0$, es fácil ver que $cR=[ca_1,cb_1]\times \dots \times [ca_n,cb_n]$. De modo que: $$|cR|=c(b_1-a_1)\times \dots \times c(b_n-a_n)=c^n (b_1-a_1)\times \dots \times (b_n-a_n)=c^n|R|. $$

Si $c<0$, entonces $cR=[cb_1,ca_1]\times \dots \times [cb_n,ca_n]$. Luego $$|cR|=(-c)(b_1-a_1)\times \dots \times (-c)(b_n-a_n)=|c|^n (b_1-a_1)\times \dots \times (b_n-a_n)=|c|^n|R|. $$

$\square$

Más adelante…

Definiremos nuestra primera noción de medida: La medida exterior, en la que el volúmen de rectángulos juega un papel fundamental.

Tarea moral

• Decimos que un conjunto $P\subseteq \mathbb{R}^n$ es un polígono especial si puede ser representado como una unión finita de rectángulos cerrados $R_1,R_2,\dots,R_m$: $$A=\bigcup_{k=1}^{m}R_k.$$
  • Demuestra que todo polígono especial $P$ se puede expresar como una unión finita de rectángulos cerrados y con interiores ajenos $P=\bigcup_{k=1}^{m’}Q_k$. ¿La descomposición es única?
  • Con $Q_1,Q_2,\dots,Q_{m’}$ como en el inciso anterior, definimos el volumen del polígono especial $P$ como: $$|P|=\sum_{k=1}^{m’}|Q_k|.$$ Demuestra que el volumen está bien definido, es decir, no depende de la colección de rectángulos con interiores ajenos $Q_1,Q_2,\dots,Q_{m’}$.
  • Sea $R_1,R_2,\dots, R_N$ una colección de rectángulos (no necesariamente cerrados), tales que $$P\subseteq \bigcup_{k=1}^{N}R_k.$$ Demuestra que $$|P|\leq \sum_{k=1}^{N}|R_k|.$$
  • Demuestra que si $P$ es un polígono especial, entonces $x+P$ y $cP$ son polígonos especiales para cualesquiera $x\in \mathbb{R}^n$ y $c\in \mathbb{R}$. Demuestra además que $|x+P|=|P|$ y $|cP|=|c|^n|P|$.
• Demuestra que la tercer proposición de la entrada sigue siendo cierta aún si los rectángulos son degenerados.

Introducción

Esta es la primera entrada correspondiente al curso de análisis matemático II. Para esta primera parte del curso estudiaremos la integración de Lebesgue, una noción de integral muy poderosa y sobre la que se construye gran parte del análisis matemático moderno. Veremos una forma precisa de definir conceptos como longitud, área, volumen y sus análogos en más dimensiones: La medida de Lebesgue, sobre la cual construiremos este concepto de integración. Luego, estudiaremos las principales propiedades de la integral de Lebesgue, su relación con la integral de Riemann y una serie de teoremas muy útiles para calcular y estimar integrales: Los teoremas de convergencia y el teorema de Fubini.

Motivación

En tus cursos anteriores seguramente te has encontrado con el concepto de integral de Riemann. Ésta es una herramienta computacional muy poderosa que, a grosso modo, nos ayuda a encontrar el «área bajo la curva» en una dimensión y sus análogos en dimensiones más altas. Sin embargo, tiene una serie de limitaciones que hacen deseable un concepto de integración más general. A modo de motivación, recapitulamos algunas de ellas:

La clase de funciones integrables en el sentido de Riemann es limitada.

Como ejemplo, considera la función de Dirichlet $\chi_{\mathbb{Q}}:[0,1] \to \mathbb{R}$ definida como:

\begin{equation*} \chi_{\mathbb{Q}}(x)= \begin{cases} 1 & \text{si } x \in \mathbb{Q}\\ 0 & \text{si } x \in \mathbb{R}\setminus\mathbb{Q} \end{cases} \end{equation*}

Observa que si $[a,b]\subseteq [0,1]$ con $a<b$ entonces $\inf_{x \in [a,b]} f(x)=0$ y $\sup_{x \in [a,b]} f(x)=1$, pues $[a,b]$ contiene números racionales e irracionales.

Recordemos que en el contexto de integrales de Riemann las sumas inferiores y superiores de la función $f$, sobre una partición $P=\{a=x_0 < x_1 < \dots < x_n=b \}$ se definen como:
$$L(f,P,[a,b])=\sum_{j=1}^{n}(x_j-x_{j-1})\inf_{[x_{j-1},x_j]}f$$ $$S(f,P,[a,b])=\sum_{j=1}^{n}(x_j-x_{j-1})\sup_{[x_{j-1},x_j]}f$$

Y se dice que la función es Riemman integrable si $$L(f,[a,b]):= \sup_P L(f,P,[a,b])$$ Y $$S(f,[a,b]):= \inf_P S(f,P,[a,b])$$ Coinciden. La integral de Riemann se define como el valor común: $$L(f,[a,b])=S(f,[a,b]).$$
En nuestro ejemplo, es fácil ver que $L(\chi_{\mathbb{Q}},P,[a,b])=0$, $S(\chi_{\mathbb{Q}},P,[a,b])=1$ para cualquier partición $P$, de modo que $$L(\chi_{\mathbb{Q}},[a,b])=0$$ Y $$S(\chi_{\mathbb{Q}},[a,b])=1.$$ Por lo que la función NO es Riemann integrable. Sin embargo, es natural pensar que la integral debería ser 0 pues hay «muy pocos racionales en comparación con los irracionales en $[0,1]$». El siguiente ejemplo refuerza esta intuición.

La integral de Riemann no se comporta bien bajo operaciones de límite.

Si consideramos alguna numeración de los números racionales en $\mathbb{Q}\cap [0,1]=\{ r_1,r_2, \dots\}$ y para cada $k\in \mathbb{Z^+}$ definimos $f_k:[0,1]\to\mathbb{R}$ como:

\begin{equation*} f_k(x)= \begin{cases} 1 & \text{si } x \in \{ r_1,r_2,\dots, r_k \}\\ 0 & \text{en otro caso } \end{cases} \end{equation*}

Se verifica que $f_k$ es Riemann integrable y $\int_0^1f_k(x) \mathrm{d} x=0$, pues $f$ es acotada y vale 0 salvo en una cantidad finita de puntos.

Observa que si $x$ es irracional, $f_k(x)=0$ $\forall k$; y si $x$ es racional, $x=r_N$ para algún $N$ de modo que $f_k(x)=1$ $\forall n\geq N$. Esto nos dice que $\chi_{\mathbb{Q}}$ es el límite puntual de la sucesión de funciones $f_k$ pero $\chi_{\mathbb{Q}}$ no es Riemann integrable.

En el ejemplo anterior la sucesión $f_k$ se puede modificar para hacerla continua o incluso suave. Piensa por ejemplo en sustituir las discontinuidades de salto por crestas de funciones lineales a pedazos o pulsos suaves cuya anchura se va haciendo arbitrariamente pequeña. En general, esto nos dice que la clase de funciones Riemann integrables no es cerrada bajo toma de límites (puntuales), ni siquiera si las funciones son «bien portadas».

Con nociones más fuertes de convergencia, por ejemplo convergencia uniforme (una hipótesis muy «fuerte»), se tienen mejores resultados respecto a toma de límites. El siguiente es bien conocido:

Teorema. Sea $f_k:[a,b]\to \mathbb{R}$, $k\in \mathbb{N}$, una sucesión de funciones Riemann integrables que convergen uniformemente a $f:[a,b]\to \mathbb{R}$. Entonces $f$ es Riemann integrable y además $$\lim_{k\to \infty}\int_a^b f_k(x) \ \mathrm{d}x=\int_a^b f(x) \ \mathrm{d}x.$$

$\square$

También en el contexto de toma de límites, otra pregunta relevante es ¿bajo qué condiciones la integral conmuta con un límite?, o al menos ¿se puede decir algo sobre la integral de un límite?. Estas son preguntas que surgen normalmente en áreas como ecuaciones diferenciales, análisis de Fourier o probabilidad, en la que muchos conceptos se definen precisamente como un límite (por ejemplo la derivada o las series de Fourier). El ejemplo anterior no es muy esperanzador pues puede que un límite puntual ni siquiera sea Riemann integrable. Bajo ciertas condiciones sí se puede decir algo, por ejemplo:

Teorema (de la convergencia acotada). Sea $f_k:[a,b] \to \mathbb{R}$ una sucesión de funciones Riemann integrables y acotadas tales que $\exists M\in \mathbb{R}$ tal que $|f_k(x)|\leq M$ para todo $k\in \mathbb{N}$ y $x\in [a,b]$. Si $f_k$ convergen puntualmente a $f$ y $f$ es Riemann integrable, entonces $$\lim_{k \to \infty} \int_{a}^{b} f_k(x) \ \mathrm{d} x=\int_{a}^{b} f(x) \ \mathrm{d} x.$$

$\square$

¿Habrá alguna noción de integración que sea más laxa respecto a toma de límites?¿Se podrán mejorar los resultados enunciados?

La integral de Riemann no maneja adecuadamente funciones no acotadas o dominios no acotados.

Por definición, la integral de Riemann se define para funciones acotadas sobre intervalos cerrados finitos. Para funciones no acotadas o dominios no acotados la forma clásica de abordar estos problemas es con integrales impropias. Considera los siguientes ejemplos:

Ejemplo. La función $f(x)=\frac{1}{\sqrt{x}}$ no está acotada en $[0,1]$, sin embargo podemos hablar de área bajo la curva con la integral impropia:

\begin{align*} \lim_{a\downarrow 0}\int_{a}^{1}f(x) \ \mathrm{d}x &= \lim_{a\downarrow 0}\int_{a}^{1}\frac{1}{\sqrt{x}}\mathrm{d}x \\ &= \lim_{a\downarrow 0} [2x^{\frac{1}{2}}]_{a}^{1} \\ &= \lim_{a\downarrow 0} [2-2\sqrt{a}] \\
&= 2
\end{align*}

$\triangle$

Ejemplo. Algo similar ocurre con $f(x)=\frac{1}{x^2}$ pero en el intervalo $[1,\infty)$:

\begin{align*} \lim_{N\to \infty}\int_{1}^{N}f(x) \ \mathrm{d}x &= \lim_{N\to \infty }\int_{1}^{N}\frac{1}{x^2}\mathrm{d}x \\ &= \lim_{N\to \infty} \left[-\frac{1}{x}\right]_{1}^{N} \\ &= \lim_{N\to \infty} \left[ 1-\frac{1}{N}\right] \\
&= 1
\end{align*}

$\triangle$

Integrales de este tipo suelen abundar en física y probabilidad. ¿Habrá algún modo de manejar este tipo de integrales de forma unificada?

Fue precisamente por esta clase de restricciones que a finales del siglo XIX se empezaron a buscar nociones distintas o más generales de integración. Fue precisamente Henri Lebesgue quien en 1901 publicó su famoso artículo Sur une généralisation de l’intégrale définie, en el que definía una noción de integración que generalizaba a la de Riemann y resolvía varias de las limitaciones que esta presentaba.

La teoría de integración de Lebesgue y la teoría de la medida han sido tremendamente exitosas en el análisis moderno y ha encontrado aplicaciones fundamentales en áreas como la probabilidad, las ecuaciones diferenciales, la física matemática, entre otras.

Bibliografía

El material presentado en estas notas se basa en elementos tomados de la siguiente bibliografía, todas excelentes fuentes de consulta.

• Folland, Gerald B. Real analysis: modern techniques and their applications. John Wiley & Sons, 1999.
• Jones, Frank. Lebesgue integration on Euclidean space. Jones & Bartlett Learning, 2001.
• Stein, Elias M., and Rami Shakarchi. Real analysis: measure theory, integration, and Hilbert spaces. Princeton University Press, 2009.
• Tao, Terence. Analysis II. Springer Singapore, 2016.
• Wheeden, Richard Lee, and Antoni Zygmund. Measure and integral. Vol. 26. New York: Dekker, 1977.

Más adelante…

Abordaremos el problema de la medida sobre los conjuntos más sencillos: los rectángulos. Veremos algunos resultados técnicos que utilizaremos a lo largo de la construcción de la medida de Lebesgue.

1. La modelación matemática en las ciencias

La modelación matemática es la herramienta que sirve para representar sistemas naturales y entender cómo funcionan, además de predecir y analizar comportamientos y encontrar soluciones de problemas sobre sistemas complejos. 

1.1. ¿Qué es y para qué sirve un modelo matemático?

¿Qué es un modelo matemático?

Un modelo matemático es una representación abstracta de un sistema real. Utiliza variables, ecuaciones matemáticas, funciones o algoritmos para describir cómo interactúan estos elementos. Como se mencionó anteriormente, los modelos son herramientas para simplificar, entender, estudiar y predecir comportamientos de sistemas complejos, como los ecosistemas, el crecimiento de poblaciones, la difusión de enfermedades, entre otros. Por ejemplo, en biología, un modelo podría representar la dinámica de una población, utilizando factores como la tasa de natalidad, mortalidad y recursos disponibles.

¿Para qué sirve un modelo matemático?

1. Predecir: los modelos matemáticos pueden predecir futuros comportamientos bajo condiciones específicas. Según Allman y Rhodes, “los modelos permiten entender las consecuencias que una ecuación puede tener a través del análisis matemático, para así poder comparar la formulación con observaciones biológicas” (Allman, p. 1). Por ejemplo, si se conoce la cantidad de individuos que tiene una población y cuántos nacen y mueren cada año, se puede predecir la población que habrá en algún momento del futuro. Esto es útil para la conservación de especies.
2. Simular: se pueden crear diferentes escenarios para explorar los resultados de diferentes intervenciones, por lo que se puede practicar la «prueba y error» las veces necesarias sin consecuencias dañinas para un ecosistema. Por ejemplo, si se deseara saber qué pasaría si se introdujera un nuevo depredador en un ecosistema, un modelo puede ayudar a ver cómo esto afectaría a la población sin tener que hacer un experimento real que podría ser perjudicial.
3. Optimizar: en algunos casos, los modelos se utilizan para encontrar la mejor estrategia o solución a un problema, como en el control de plagas, sin embargo, la optimización busca no solo eficiencia, sino también sostenibilidad y equilibrio en la gestión de recursos naturales, Britton señala que “las políticas de gestión de recursos pueden derivarse de modelos matemáticos” (Britton, p. 45). Por ejemplo, si se trabaja en la gestión de un área natural, es posible usar un modelo para determinar cómo distribuir los recursos de manera eficiente, asegurando tanto la salud del ecosistema como su sostenibilidad a largo plazo.
4. Comprender: los modelos también son herramientas educativas, ayudan a visualizar y entender relaciones complejas. Según Kline, “las matemáticas nos permiten observar patrones y relaciones” (Kline, p. 5), al representar gráficamente los datos y las relaciones, se pueden observar patrones que no son obvios sólo al mirar los números.

1.2. De la biología al modelo y de regreso: Supuestos, limitaciones y predicciones verificables

Para pasar de un fenómeno biológico real a un modelo matemático se deben hacer suposiciones que son fundamentales para construir dicho modelo, pero es importante considerar que también imponen limitaciones sobre qué tan exacto o útil será en ciertos contextos. Los sistemas biológicos pueden involucrar una “gran cantidad de interacciones y predisposiciones que compiten entre sí, lo que puede dificultar la comprensión completa de un fenómeno en su totalidad” (Allman, p. 1). Por esta razón, los modelos matemáticos deben simplificar estos sistemas, enfocándose en los factores más relevantes, pero esta simplificación puede llevar a la omisión de detalles importantes y afectar la precisión de las predicciones en algunos escenarios.

Observación. Todo comienza con la observación, es importante prestar atención a todas las variables que pueden intervenir o afectar el desarrollo de un evento.

Supuestos. Al momento de realizar suposiciones se deben considerar aspectos como
• Homogeneidad: suposición de que el sistema es uniforme en ciertas características, por ejemplo, asumir que todos los individuos de una población tienen la misma tasa de crecimiento.
• Condiciones iniciales conocidas: los modelos suelen necesitar condiciones iniciales específicas para poder ser resueltos, por ejemplo, la cantidad inicial de individuos en una población.
• Aislamiento de factores externos: a veces se puede asumir que el sistema es cerrado, es decir, que no influyen factores externos, para facilitar el análisis.

Limitaciones. Los modelos son abstracciones de la realidad que nunca podrán representar todos los factores posibles que influyen en un sistema biológico, por lo que es importante reconocer que todos los modelos tienen limitaciones.
Según Allman, “aunque muchos de los modelos que examinamos pueden parecer al principio simplificaciones burdas, su misma simplicidad es una fortaleza. Los modelos simples muestran claramente las implicaciones de nuestros supuestos más básicos» (Allman, p . 1). En otras palabras, aunque los modelos matemáticos omiten muchos detalles, esta simplificación les permite centrarse en los aspectos fundamentales del fenómeno. Por ejemplo, en un modelo de crecimiento poblacional tal  vez no se consideren detalles como la competencia entre especies o las interacciones con otras especies.
Otra limitación puede ser la escalabilidad; un modelo que funciona a pequeña escala (como en un laboratorio) puede no ser válido cuando se aplica a una escala mayor (por ejemplo, en un ecosistema natural).

Predicciones verificables. Los modelos matemáticos tienen que ser capaces de hacer predicciones que puedan ser verificadas empíricamente mediante experimentos u observaciones. Es fundamental que un modelo no solo explique o demuestre lo que ya se sabe, sino que también permita visualizar comportamientos futuros. Si las predicciones del modelo se verifican mediante datos reales, esto aumenta la confiabilidad del modelo. 

Ejemplo
Imagina que estás modelando el crecimiento de una población de bacterias. Supón que el modelo establece que la población crece de acuerdo con la ecuación de Malthus. Si realizas experimentos y observas que la población crece más lentamente debido a la competencia por recursos, tu modelo necesitará ajustarse para reflejar este nuevo factor (por ejemplo, usando un modelo logístico que limite el crecimiento cuando la población se acerca a la capacidad de carga).

Pasos para crear un modelo.
Supongamos que estamos interesados en modelar el crecimiento de una población de bacterias en un cultivo cerrado -es decir, sin interferencia externa- en un laboratorio, donde la bacteria se reproduce a través de divisiones celulares. Empezaremos desde la observación y avanzaremos paso a paso.

1. Observación. En este caso, se pueden hacer las siguientes observaciones:

• Se sabe que las bacterias en un cultivo crecen a una tasa proporcional a su población actual.
• En un principio, se tiene un número pequeño de bacterias (supongamos 100), y después de cierto tiempo, el número de bacterias aumenta.
• No hay depredadores, no hay competencia por recursos en las primeras etapas, y el entorno es ideal para su crecimiento.

2. Identificación de Variables. En cualquier modelo, primero es necesario identificar las variables involucradas.

• Variable dependiente (a modelar): N(t) es el número de bacterias en el tiempo t.
• Variable independiente: t es el tiempo, generalmente en horas, días, o cualquier unidad pertinente.
• Parámetro constante: r es la tasa de crecimiento de la población (la tasa de natalidad). Esto indica cuántas bacterias nuevas nacen por cada bacteria existente en un tiempo determinado.

3. Supuestos. Para simplificar el problema y poder construir un modelo matemático, necesitamos hacer algunos supuestos que describen cómo el sistema se comporta:

• Supuesto 1: El entorno es ideal para el crecimiento bacteriano; no hay limitación de recursos.
• Supuesto 2: La tasa de crecimiento r es constante durante todo el proceso.
• Supuesto 3: Las bacterias se dividen de manera exponencial, es decir, cada bacteria produce exactamente dos hijas en un tiempo fijo.
• Supuesto 4: El número de bacterias en el tiempo t = 0 es conocido, es decir, tenemos un número inicial $N_0$​ de bacterias.

4. Limitaciones. Ahora, debemos tener en cuenta algunas limitaciones que podrían afectar la validez de nuestro modelo:

• Limitación 1: Este modelo no tiene en cuenta mutaciones o factores estocásticos (azar), como la posibilidad de que algunas bacterias no se reproduzcan debido a variabilidad genética o factores aleatorios.
• Limitación 2: El modelo no incluye interacciones con otras especies, como bacterias depredadoras o interacciones simbióticas que podrían alterar el crecimiento.

5. Formulación del modelo. El siguiente paso es escribir la ecuación matemática que describe el fenómeno. Con base en nuestras observaciones, sabemos que el crecimiento bacteriano sigue una ley de crecimiento exponencial. En el capítulo 1, Britton discute el crecimiento de poblaciones y la ecuación diferencial $\frac{dN}{dt} = r N(t)$ –que es ampliamente utilizada para modelar este tipo de fenómenos–, donde:

• $\frac{dN}{dt}$​ es la tasa de cambio de la población de bacterias con respecto al tiempo (es decir, cuántas bacterias están naciendo por unidad de tiempo),
• r es la tasa de crecimiento de la población,
• N(t) es el número de bacterias en el tiempo t.

Esta es una ecuación diferencial que describe cómo cambia la población de bacterias con el tiempo. Para obtener la expresión de N(t), resolvemos esta ecuación diferencial. La solución es:

$N(t) = N_0 e^{rt}$

donde

• $N_0$ es el número inicial de bacterias en t = 0,
• e es la base del logaritmo natural.

Este modelo nos dice que el número de bacterias crece exponencialmente en función del tiempo, con una tasa de crecimiento r.

6. Verificación del Modelo. Finalmente, se verifica el modelo utilizando datos reales o se realiza el experimento para comprobar si las predicciones del modelo son correctas.

Un caso práctico de verificación
Supongamos que, en un experimento real, comenzamos con una población de 100 bacterias (es decir, $N_0 = 100$) y que después de 2 horas ya hay 400 bacterias.
Para comprobar si el modelo puede predecir este comportamiento usamos la fórmula del modelo: 

$N(t) = N_0 e^{rt}$

Sabemos que $N_0 = 100$, t = 2 horas, y N(t) = 400. Sustituimos en la fórmula

$400 = 100 e^{r \cdot 2}$

Despejamos r

$4 = e^{2r}$

Tomamos el logaritmo natural en ambos lados

$\ln(4) = 2r$

$r = \frac{\ln(4)}{2} \approx 0.6931$

Ahora, sabemos que la tasa de crecimiento r es aproximadamente 0.6931 por hora. Podemos usar este valor para hacer más predicciones y compararlas con los datos reales.

Predicción adicional
Supongamos que queremos saber cuántas bacterias habrá después de 5 horas. Usamos el modelo con r = 0.6931:

$N(5) = 100 e^{0.6931 \cdot 5} = 100 e^{3.4655} \approx 100 \cdot 32 = 3200$

Esto nos da una predicción de que habrá 3200 bacterias después de 5 horas.

Si el número real de bacterias se acerca a este valor, podemos estar bastante seguros de que nuestro modelo está funcionando bien. Si no es así, será necesario ajustar el modelo, considerar efectos de límite de recursos (como el modelo logístico), o incorporar factores estocásticos.

Resumen del procedimiento:

1. Observación: se identifica el fenómeno a estudiar (crecimiento de bacterias).
2. Identificación de variables: se determina qué variables son importantes (número de bacterias, tiempo, tasa de crecimiento).
3. Supuestos: se realizan suposiciones sobre el entorno ideal, el crecimiento exponencial y las condiciones iniciales.
4. Limitaciones: se considera que el modelo tiene limitaciones como el crecimiento ilimitado y la falta de factores estocásticos.
5. Formulación del modelo: se desarrolla una ecuación diferencial para modelar el crecimiento exponencial de las bacterias.
6. Verificación: se comprueban las predicciones del modelo con datos reales del experimento.

1.3. Tipos de modelos: Deterministas vs. Estocásticos

Modelos deterministas. Son aquellos que producen resultados predecibles, es decir que están completamente definidos y se puede calcular exactamente lo que sucederá. En otras palabras, no hay incertidumbre; dado un conjunto de condiciones iniciales y parámetros, el modelo siempre dará el mismo resultado. Como menciona Britton, en un modelo determinista, “el estado del sistema en el tiempo t + 1 se determina completamente a partir del estado en el tiempo t» (Britton, p. 2). Estos modelos se suelen representar con ecuaciones diferenciales o sistemas algebraicos que describen el comportamiento del sistema en función del tiempo.

Por ejemplo, el modelo de crecimiento exponencial es un modelo determinista, donde la población crece de manera predecible si no hay factores limitantes: $N(t) = N_0 e^{rt}$ donde N(t) es el tamaño de la población en el tiempo t, $N_0$​ es el tamaño inicial de la población, y r es la tasa de crecimiento constante.

Modelos estocásticos. En estos modelos hay incertidumbre, el azar juega un papel importante. Los resultados pueden variar incluso con las mismas condiciones iniciales; el sistema no sigue un camino único, sino que puede tener varios resultados posibles debido a la inclusión de variables aleatorias o probabilísticas. Son útiles cuando se requiere modelar fenómenos como las fluctuaciones en una población debido a factores aleatorios (mutaciones genéticas, migración, dispersión). Un ejemplo claro puede ser la modelación de la propagación de una enfermedad infecciosa en una población, donde la tasa de infección no es constante, sino que depende de la probabilidad de contacto entre individuos. En un modelo estocástico, la distribución de probabilidades es clave.

Referencias bibliográficas

Allman, E. S. & J. A. Rhodes. 2007. Mathematical models in biology: an introduction. Cambridge University Press, Cambridge.
Britton, N. F. 2003. Essential mathematical biology. Springer, Cham.
Kline, M. 1967. Mathematics for the nonmatemathician. Dover, Nueva York.

Evaluación

1. Responde y haz lo que se indica

a. ¿Qué es un modelo matemático?
Escribe una definición simple de qué es un modelo matemático en el contexto de las ciencias. Explica brevemente por qué es útil tener un modelo en lugar de estudiar un fenómeno de forma directa.

b. Menciona al menos tres ventajas de usar modelos matemáticos en biología.

c. Define qué son los supuestos en un modelo matemático.
Da un ejemplo de un supuesto que podrías hacer si estás modelando el crecimiento de una población de bacterias.

d. ¿Por qué es importante conocer las limitaciones de un modelo matemático?
Explica qué podría suceder si un modelo no tiene en cuenta factores importantes (como la competencia entre especies o los recursos limitados en un ecosistema).

e. Explica la diferencia entre un modelo determinista y un modelo estocástico.
Usa un ejemplo sencillo para ilustrar la diferencia. Por ejemplo, si estás modelando el crecimiento de una población de bacterias, ¿cuál sería un modelo determinista y cuál uno estocástico?

f. Imagina que estás modelando el crecimiento de una población de animales en un hábitat. Si se incluye una probabilidad de que cada individuo muera debido a condiciones ambientales impredecibles, ¿cómo se llamaría este tipo de modelo? Justifica tu respuesta.

g. Imagina que tienes una población de 1000 bacterias en un cultivo cerrado. Esta población crece a una tasa constante de 0.2 por hora. Si se mantiene esta tasa de crecimiento, ¿cómo describirías el comportamiento de la población en términos matemáticos?

h. ¿Este es un modelo determinista o estocástico? ¿Por qué?

Respuesta modelo: Este modelo es determinista, ya que asume que la tasa de crecimiento es constante, r = 0.2, y que el crecimiento de la población depende únicamente de este parámetro, sin ningún componente aleatorio.

i. ¿Cuáles serían algunos supuestos de este modelo?
Piensa en qué asumes sobre el comportamiento de las bacterias, el ambiente, o cualquier otro factor relevante.

j. ¿Por qué es importante verificar las predicciones de un modelo matemático con datos reales o experimentales?
Explica cómo se puede hacer para comprobar si un modelo matemático está funcionando correctamente.

k. Si tienes un modelo de crecimiento de una población de plantas en un invernadero, ¿qué tipo de datos recolectarías para comparar con las predicciones del modelo?

Pregunta de Reflexión:

• ¿Qué importancia tiene comprender los supuestos y las limitaciones de un modelo matemático cuando se usan para tomar decisiones en biología (por ejemplo, para la conservación de especies, el manejo de recursos naturales, etc.)?

2. Proporciones, concentraciones y soluciones

Las proporciones nos permiten comparar partes de un todo y entender las relaciones cuantitativas entre diferentes elementos. Las concentraciones son esenciales para comprender cómo interactúan los compuestos en soluciones, lo cual es crucial para procesos biológicos como la difusión de nutrientes, el transporte de gases y la regulación de los ecosistemas.

2.1. Representación de fracciones en forma decimal y porcentual

Las fracciones, decimales y porcentajes son tres formas diferentes de representar una parte de un todo. Estos tres conceptos se utilizan en biología para representar datos relacionados con concentraciones, proporciones de especies en una población, etc.

1. Una fracción es una forma de representar una parte de una unidad. Se representa como $\frac{a}{b}$​, donde a es la parte y b es el todo, por ejemplo, $\frac{1}{2}, \frac{3}{4}$, etc.
2. Un número decimal es una fracción cuyo denominador es una potencia de 10, y se utiliza la notación posicional para expresar las fracciones de manera más sencilla. Los números decimales pueden clasificarse en tres tipos:

Decimales exactos: son aquellos que tienen un número finito de dígitos después del punto decimal. Por ejemplo, $0.5 = \frac{1}{2}$ o $0.75 = \frac{3}{4}.$

Decimales periódicos: son los que, después del punto decimal, tiene una cola infinita de decimales en un patrón fijo, este patrón se denomina período. Por ejemplo, el número $0.\overline{3}$, que es igual a $\frac{1}{3}$, tiene un período de 3. Otro ejemplo es $0.\overline{142857}$ que es equivalente a $\frac{1}{7}. Siempre son racionales.$

Decimales no periódicos: son aquellos que no repiten ningún patrón y tienen una secuencia infinita de dígitos después del punto decimal. Un ejemplo de este tipo de decimal es $\pi = 3.14159265358979…$, que continúa sin repetirse y sin un patrón predecible. Los decimales no periódicos corresponden a números irracionales.

3. Porcentajes: es una forma de expresar un número como una fracción de 100, es decir, una fracción multiplicada por 100, por ejemplo $\frac{1}{2} = 0.5 = 50 %$.

Ejemplo. Si se tiene una solución con 25 gramos de sal disueltos en 500 gramos de agua, ¿cuál es la concentración de sal en porcentaje?
Paso 1. Se calcula la fracción de sal: $\frac{25}{500} = \frac{1}{20} = 0.05$.
Paso 2. Para convertirlo a porcentaje, se multiplica por 100: 0.05 × 100 = 5 %.
Esto significa que la solución tiene una concentración del 5 % de sal.

Ejercicio. Si se tiene una solución con 10 gramos de azúcar disueltos en 250 gramos de agua, ¿cuál es la concentración de azúcar en porcentaje?

2.2. Aplicaciones: concentraciones (salinidad, CO₂ atmosférico), preparación de soluciones

Las concentraciones son importantes para entender muchos procesos biológicos, por ejemplo para medir la cantidad de alguna sustancia en un medio. Se pueden expresar de diferentes formas, como la concentración molar, la fracción molar, la molalidad, entre otras; esto es fundamental en áreas como la biología celular, la ecología (concentración de gases como CO₂ en la atmósfera) o la farmacología (concentración de medicamentos en sangre). 

Concentración molar (M)
La molaridad (M) es una medida de concentración que expresa la cantidad de moles de soluto por litro de solución. Un mol es una unidad utilizada en química para expresar una cantidad específica de partículas como átomos, moléculas o iones. Un mol contiene aproximadamente $6.022 \times 10^{23}$ partículas, un número conocido como el número de Avogadro. La concentración molar se define matemáticamente de la siguiente manera:

$M = \frac{\text{moles de soluto}}{\text{volumen de solución en litros}}$

Ejemplo. Si se disuelve 1 mol de NaCl (sal común) en 1 L de agua, entonces la solución tendrá una concentración de 1 M.

Concentración en porcentaje (porcentaje en masa)
A veces se utilizan porcentajes para expresar la concentración de una solución en términos de la masa de soluto respecto a la masa total de la solución, y se calcula de la siguiente manera:

$\text{Porcentaje en masa} = \left( \frac{\text{masa de soluto}}{\text{masa de solución}} \right) \times 100$

Ejemplo. Si se tienen 10 g de sal disueltos en 90 g de agua, ¿cuál sería la concentración en porcentaje?

$\frac{10 \, \text{g}}{100 \, \text{g}} \times 100 = 10 %$

Salinidad
Se refiere a la cantidad de sal disuelta en agua. Es un concepto de importante uso por ejemplo en los ecosistemas marinos, para medir la salinidad y entender el equilibrio de especies acuáticas. Se puede expresar como partes por mil (ppm), que equivale a la masa de sal disuelta en mil partes de agua. En volumen, 1 ppm = 1 mL por m³ = 1 μL por litro.

Ejemplo. En el océano, la salinidad promedio es de aproximadamente 35 ppt, por lo tanto, en cada litro de agua hay 35 gramos de sales disueltas.

Ejercicio. Si se tienen 200 mL de agua y se añaden 10 g de sal, ¿cuál será la concentración de sal en la solución?

Concentración de CO₂
Para la biología ambiental, medir la concentración atmosférica de dióxido de carbono, CO₂, es esencial para estudiar el cambio climático y su impacto sobre los ecosistemas. Se expresa en partes por millón (ppm), esto indica cuántas moléculas de CO₂ hay por cada millón de moléculas de aire.

Ejercicio. Si la concentración de CO₂ en la atmósfera es de 400 ppm (partes por millón), esto significa que en un millón de partes de aire, 400 partes son de CO₂. Si se tiene 1 litro de aire, ¿cuántos mililitros de CO₂ hay en ese volumen?

Ejercicio. En un ambiente cerrado, la concentración de oxígeno es del 21 %. Si hay 50 litros de aire, ¿cuántos litros de oxígeno hay en total?

2.3. Conversión entre porcentajes, fracciones y cantidades absolutas

La conversión entre fracciones, porcentajes y cantidades absolutas es frecuente cuando se trabaja con datos biológicos como concentraciones en soluciones, porcentajes de población o mediciones de otros parámetros biológicos, por dar algunos ejemplos. 

Conversión de fracción a porcentaje 
Para convertir una fracción a porcentaje, se debe encontrar una fracción equivalente cuyo denominador sea 100, ya que buscamos la cantidad n de cada 100, es decir, el tanto por ciento. Basta con multiplicar la fracción por 100. Otra opción puede ser convertir primero la fracción a número decimal realizando la división, y luego multiplicar por 100.

Ejemplo. Si una población tiene $\frac{1}{5}$​ de individuos infectados por una enfermedad, ¿a qué porcentaje de la población equivale?

$\frac{1}{5}​ = \frac{x}{100}  \Rightarrow \frac{1}{5}​​ \times 100 = 20$,

o bien $\frac{1}{5}​ = 0.2  \Rightarrow 0.2​​ \times 100 = 20$.

Entonces $\frac{1}{5}$ de individuos equivale al 20 % de la población.

Ejercicio. Si en un grupo de 40 estudiantes, 10 han completado su tarea. ¿Qué porcentaje de estudiantes ha completado su tarea?

Ejercicio. Si en una población de 200 árboles, 60 son de especies invasoras. ¿Qué porcentaje de los árboles corresponde a los no nativos?

Conversión de porcentaje a fracción
Para convertir un porcentaje a fracción se debe dividir entre 100 para obtener la fracción decimal que luego se simplificará.

Ejemplo. Si el 30% de una solución es NaCl (sal), ¿qué fracción representa esta concentración?
$30 % = \frac{30}{100}$, luego se simplifica la fracción dividiendo tanto el numerador como el denominador entre su máximo común divisor (MCD), en este caso es 10:  

$\frac{30}{100} = \frac{3}{10}$

Por lo tanto, 30% equivale a $\frac{3}{10}$​.

Ejercicio. Si el 40% de una población de bacterias está infectada, ¿qué fracción representa el porcentaje de bacterias infectadas?

Conversión de un porcentaje a cantidad absoluta
A veces es útil o necesario convertir un porcentaje a una cantidad absoluta, por ejemplo de una sustancia en una solución o población. Esto es particularmente útil cuando se manejan concentraciones en una solución o porcentajes en una muestra biológica. Para convertir un porcentaje a cantidad absoluta, se puede encontrar su expresión en fracción decimal y luego multiplicar por el total.

Ejemplo. Si se tiene una solución de 500 mL y la concentración de sal es del 10 %, ¿de cuánto sería la cantidad de sal en la solución?

$10\% = \frac{10}{100} = 0.1 \Rightarrow 0.1 \times 500 \, \text{mL}$

$ 10\% = 50 \, \text{mL de sal}$.

Ejercicio. Si un ecosistema tiene 1000 g de carbono y el 20 % está almacenado en las raíces de las plantas, ¿cuántos gramos de carbono están almacenados en las raíces?

Ejercicio. Si en un ecosistema con 5000 g de nitrógeno, el 15 % está presente en el suelo, ¿cuántos gramos de nitrógeno hay en el suelo?

Conversión de cantidad absoluta a porcentaje
Si tienes una cantidad conocida de una sustancia en una solución y quieres expresar su concentración en porcentaje, puedes usar la fórmula:

$\text{Porcentaje} = \left( \frac{\text{cantidad de soluto}}{\text{cantidad total de la solución}} \right) \times 100$

Ejemplo. Si en un recipiente con 500 g de una solución hay 125 g de azúcar, ¿qué porcentaje de la solución es azúcar?

$\frac{125}{500} \times 100 = 25$, por lo tanto, 25 % de la solución es azúcar.

Ejercicio. Si en una solución de 600 g, 150 g corresponden a sal, ¿qué porcentaje de la solución es sal?

Conversión de fracción a cantidad absoluta
Para convertir una fracción a cantidad absoluta, se multiplica el total por la fracción.

Ejemplo. Si en una muestra de 200 g de agua, $\frac{3}{4}$​ es agua dulce, ¿cuántos gramos de agua dulce hay? 

Para convertir una fracción a cantidad absoluta, multiplicamos el total (200 g) por la fracción:

$200 \times \frac{3}{4} = 150$, por lo tanto, 150 g de la muestra corresponden a agua dulce.

Ejercicio. En una solución de 1000 g de sangre, $\frac{2}{5}$​ es plasma. ¿Cuántos gramos de plasma hay en la muestra? 

Evaluación. Proporciones, concentraciones y soluciones

1. Responde

a. En un estudio ecológico, se observa que de un total de 1000 árboles en un bosque, 300 son de una especie invasora. ¿Qué porcentaje de los árboles del bosque son de especies invasoras?

b. En una población de 1200 bacterias, 0.75 de ellas están infectadas por una enfermedad. ¿Qué fracción representa la población infectada?

c. Si una solución tiene 50 gramos de azúcar disueltos en 200 gramos de agua, ¿cuál es la concentración de azúcar en porcentaje?

d. En un ecosistema marino, la salinidad promedio es de 35 ppt. ¿Cuántos gramos de sal hay disueltos en 2 litros de agua?

e. Una solución acuosa contiene 2 moles de NaCl (sal común) disueltos en 1 litro de agua. ¿Cuál es la concentración molar de la solución?

f. En un laboratorio, se preparó una solución disolviendo 15 gramos de glucosa (C₆H₁₂O₆) en 150 ml de agua. Si la densidad del agua es aproximadamente 1 g/ml, ¿cuál es la concentración de glucosa en porcentaje en masa?

g. La concentración de CO₂ en la atmósfera es de 400 ppm. Si tomamos una muestra de aire de 2 metros cúbicos (2000 litros), ¿cuántos litros de CO₂ están presentes en esa muestra?

h. En un ecosistema terrestre, se sabe que el 20 % del nitrógeno en el suelo está presente como amoníaco (NH₃). Si en total hay 3000 g de nitrógeno en el suelo, ¿cuántos gramos de nitrógeno están presentes como amoníaco?

i. Si el 15 % de una población de 2000 insectos está infectada por un virus, ¿cuántos insectos están infectados?

j. En un ecosistema acuático, el 40 % del oxígeno en el agua es consumido por organismos acuáticos. Si hay 5000 litros de agua en un estanque, ¿cuántos litros de oxígeno son consumidos por los organismos?

k. Si en una solución de 300 mL de agua, el 10 % está compuesto por sales minerales, ¿cuál es la cantidad absoluta de sales en la solución?

l. Un investigador mide que en un ecosistema existen 100 g de carbono. Si el 25 % de ese carbono está almacenado en las raíces de las plantas, ¿cuántos gramos de carbono están almacenados en las raíces?

m. Si en una solución de 400 g de agua, $\frac{2}{5}$​ de ella es agua dulce, ¿cuántos gramos de agua dulce hay en la solución?

n. En un ecosistema forestal, la fracción de árboles jóvenes es $\frac{3}{8}$​. Si hay un total de 1600 árboles en el bosque, ¿cuántos árboles son jóvenes?

o. En un laboratorio de biología, se prepara una solución con 250 g de una sustancia en 1250 g de agua. ¿Cuál es la concentración de la sustancia en porcentaje?

p. Una solución tiene una concentración de 5 % de NaCl en masa. Si la masa total de la solución es 400 g, ¿cuántos gramos de NaCl hay en la solución?

q. En un ecosistema marino, la salinidad es de 40 ppt. Si se tiene 500 litros de agua de mar, ¿cuántos gramos de sal hay disueltos en esa cantidad de agua?

r. Un experimento muestra que el 30 % del oxígeno en una muestra de aire está en forma de ozono (O₃). Si hay 2000 mL de aire, ¿cuántos mililitros de ozono hay en la muestra?

s. En una plantación de árboles, el 40 % de los árboles son de una especie nativa y el resto son de especies no nativas. Si hay 1200 árboles en total, ¿cuántos árboles son no nativos? Si además, del 40 % de árboles de especies nativas, 15 % son especies en peligro de extinción, ¿a qué porcentaje del total representa esa cantidad?

t. Si en un ecosistema hay 5 toneladas de carbono, y el 40 % de ese carbono se encuentra almacenado en los organismos del ecosistema, ¿cuántas toneladas de carbono están almacenadas en los organismos?

u. La concentración de dióxido de carbono (CO₂) en un ambiente cerrado es de 500 ppm. Si el volumen total de aire es 10 m³ (10 000 L), ¿cuántos mililitros de CO₂ están presentes en el ambiente?

v. En un experimento de difusión, se encontró que el 25 % de las partículas de un gas están dispersas en una zona de 400 mL. ¿Cuántos mililitros de gas están dispersos en esa zona?