Introduccion
La interpretación geométrica de un diferencial en cálculo está relacionada con el cambio local de una función, es deicr, cómo cambia su función cuando varía por poco las entradas de la función. En otras palabras representa una aproximación lineal al cambio de una función.
Diferenciales de funciones $f:A\subset\mathbb{R}^{2}\rightarrow\mathbb{R}$
Tenemos que $f:A\subset\mathbb{R}^{2}\rightarrow\mathbb{R}$ es diferenciable si
$$f(x_{o}+h_{1},y_{0}+h_{2})=f(x_{0},y_{0})+\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}+r(h_{1},h_{2})$$
cumple
$$\lim_{(h_{1},h_{2})\rightarrow(0,0)}\frac{r(h_{1},h_{2})}{|(h_{1},h_{2})|}=0$$
Esto se puede escribir como
$$f(x_{o}+h_{1},y_{0}+h_{2})-f(x_{0},y_{0})=\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}+r(h_{1},h_{2})$$
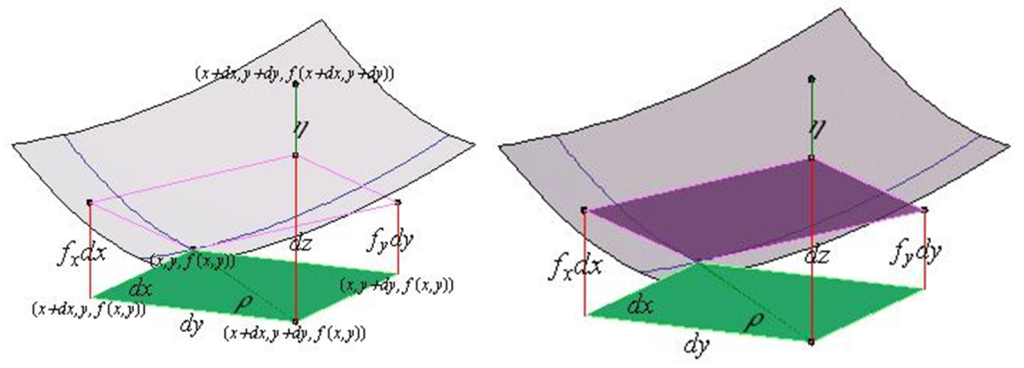
tomando
$$f(x_{o}+h_{1},y_{0}+h_{2})-f(x_{0},y_{0})=\triangle z$$
$$\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}=\frac{\partial f}{\partial x}(x_{0},y_{0})\triangle x$$
$$\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}=\frac{\partial f}{\partial y}(x_{0},y_{0})\triangle y$$
tenemos que
$$\triangle z=\frac{\partial f}{\partial x}(x_{0},y_{0})\triangle x+\frac{\partial f}{\partial y}(x_{0},y_{0})\triangle y+r(\triangle x,\triangle y)$$
haciendo $\triangle x,~\triangle y\rightarrow 0$ tenemos
$$dz=\frac{\partial f}{\partial x}(x_{0},y_{0})dx+\frac{\partial f}{\partial y}(x_{0},y_{0}) dy$$
$\textbf{Definición.}$Si $z=f(x,y)$ es una función diferenciable, la diferencial de f denotada $dz$ se define
$$dz=\frac{\partial f}{\partial x}(x_{0},y_{0})dx+\frac{\partial f}{\partial y}(x_{0},y_{0}) dy$$
$\textbf{Ejemplo.}$ Calcular la diferencial de $z=4x^{2}-xy$\En este caso
$$dz=\frac{\partial (4x^{2}-xy)}{\partial x}dx+\frac{\partial (4x^{2}-xy)}{\partial y}dy=(8x-y)dx-xdy$$
Ahora bien
$$f(x_{o}+h_{1},y_{0}+h_{2})-f(x_{0},y_{0})=\triangle z\approx \frac{\partial f}{\partial x}(x_{0},y_{0})\triangle x+\frac{\partial f}{\partial y}(x_{0},y_{0})\triangle y$$
expresa el cambio aproximado de $z=f(x,y)$ cuando $(x,y)$ pasa a $(x+\triangle x,y+\triangle y)$
Ejemplo. Aproximar el cambio de $z=4x^{2}-xy$ cuando $(x,y)$ pasa de $(2,1)$ a $(2.1,1.5)$\
En este caso tomamos $x_{0}=2$, $y_{0}=1$, $\triangle x=0.1$ y $\triangle y=.5$ y el valor de cambio será
$$\frac{\partial f}{\partial x}(2,1)\triangle x+\frac{\partial f}{\partial y}(2,1)\triangle y=(15)(0.1)-2(0.5)=1.5$$
mientras que
$$f(2.1,1.5)-f(2,1)=14.49-14=0.49$$
por lo tanto en la aproximacion se cometió un error de $0.01$
Ejemplo. Usando diferenciales se quiere calcular aproximadamente
$$A=\frac{0.97}{\sqrt{15.05}+\sqrt[3]{0.98}}$$
Solución. Considerando la función
$$f(x,y,z)=\frac{x}{\sqrt{y+\sqrt[3]{z}}}$$
con $x=1$, $y=15$, $z=1$, $dx=-0.03$, $dy=0.05$ y $dz=-0.02$ se tiene
$$f(x+dx,y+dy,z+dz)=f(x,y,z)+df(x,y,z)$$
en este caso
$$f(x,y,z)=f(1,15,1)=\frac{1}{4}$$
$$\frac{\partial f}{\partial x}=\frac{1}{\sqrt{y}+\sqrt[3]{z}},~\frac{\partial f}{\partial y}=-\frac{x}{2}\left(y+\sqrt[3]{z}\right)^{\frac{-3}{2}},~\frac{\partial f}{\partial z}=-\frac{x}{2}(y+\sqrt[3]{z})^{\frac{-3}{2}}\frac{1}{3}z^{\frac{-2}{3}}$$
evaluando en $(1,15,1)$ se tiene
$$\frac{\partial f}{\partial x}(1,15,1)=\frac{1}{4},~\frac{\partial f}{\partial y}(1,15,1)=-\frac{1}{128},~\frac{\partial f}{\partial z}(1,15,1)=-\frac{1}{384}$$
de modo que
$$df(1,15,1)=\frac{1}{4}(-0.03)-\frac{1}{128}(0.05)-\frac{1}{384}(-0.02)=-\frac{3.01}{384}$$
por lo que
$$A=\frac{1}{4}-\frac{3.01}{384}=0.242161$$
(el valor es $0.2421726$)
Diferencial de orden 2
Si $\displaystyle{df=\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy}$ entonces una diferencial de orden 2 seria:
$$d^{2}f=d(df)=d\left(\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy\right)=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy\right)dx+\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy\right)dy$$
$$=\left(\frac{\partial^{2} f}{\partial x^{2}}dx+\frac{\partial^{2} f}{\partial x\partial y}dy\right)dx+\left(\frac{\partial^{2} f}{\partial y\partial x}dx+\frac{\partial^{2} f}{\partial y^{2}}dy\right)dy=\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y\partial x}dydx+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}$$
$$=\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}$$
Por lo tanto
$$d^{2}f=d(df)=\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}$$
Ejemplo. Hallar la diferencial de orden 2 para $f(x,y)=e^{x^{2}+y^{y}}$
Solución. En este caso tenemos la fórmula
$$d^{2}f=d(df)=\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}$$
vamos a calcular las derivadas parciales correspondientes
$$\frac{\partial(e^{x^{2}+y^{2}})}{\partial x}=2xe^{x^{2}+y^{2}}$$
$$\frac{\partial(e^{x^{2}+y^{2}})}{\partial y}=2ye^{x^{2}+y^{2}}$$
$$\frac{\partial^{2}(e^{x^{2}+y^{2}})}{\partial x^{2}}=\frac{\partial}{\partial x}\left(\frac{\partial(e^{x^{2}+y^{2}})}{\partial x}\right)=\frac{\partial(2xe^{x^{2}+y^{2}})}{\partial x}=4x^{2}e^{x^{2}+y^{2}}+2e^{x^{2}+y^{2}}$$
$$\frac{\partial^{2}(e^{x^{2}+y^{2}})}{\partial y^{2}}=\frac{\partial}{\partial y}\left(\frac{\partial(e^{x^{2}+y^{2}})}{\partial y}\right)=\frac{\partial(2ye^{x^{2}+y^{2}})}{\partial y}=4y^{2}e^{x^{2}+y^{2}}+2e^{x^{2}+y^{2}}$$
$$\frac{\partial^{2}(e^{x^{2}+y^{2}})}{\partial y\partial x}=\frac{\partial}{\partial y}\left(\frac{\partial(e^{x^{2}+y^{2}})}{\partial x}\right)=\frac{\partial (2xe^{x^{2}+y^{2}})}{\partial y}=4xye^{x^{2}+y^{2}}$$
$$\frac{\partial^{2}(e^{x^{2}+y^{2}})}{\partial x\partial y}=\frac{\partial}{\partial x}\left(\frac{\partial(e^{x^{2}+y^{2}})}{\partial y}\right)=\frac{\partial (2ye^{x^{2}+y^{2}})}{\partial x}=4xye^{x^{2}+y^{2}}$$
y la diferencial de orden 2 sería:
$$d^{2}f=\left(4x^{2}e^{x^{2}+y^{2}}+2e^{x^{2}+y^{2}}\right)dx^{2}+8xye^{x^{2}+y^{2}}dxdy+\left(4y^{2}e^{x^{2}+y^{2}}+2e^{x^{2}+y^{2}}\right)dy^{2}$$
Diferencial de orden 3
Si $\displaystyle{d^{2}f=\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}}$ entonces una diferencial de orden 3 seria:
$$d^{3}f=d(d^{2}f)=d\left(\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}\right)=$$
$$\frac{\partial}{\partial x}\left(\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}\right)dx+\frac{\partial}{\partial y}\left(\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}\right)dy=$$
$$\left(\frac{\partial^{3} f}{\partial x^{3}}dx^{2}+2\frac{\partial^{3} f}{\partial x^{2}\partial y}dxdy+\frac{\partial^{3} f}{\partial x\partial y^{2}}dy^{2}\right)dx+\left(\frac{\partial^{3} f}{\partial x^{2} \partial y}dx^{2}+2\frac{\partial^{3} f}{\partial x\partial y^{2}}dxdy+\frac{\partial^{3} f}{\partial y^{3}}dy^{2}\right)dy=$$
$$\frac{\partial^{3} f}{\partial x^{3}}dx^{3}+2\frac{\partial^{3} f}{\partial x^{2}\partial y}dx^{2}dy+\frac{\partial^{3} f}{\partial x\partial y^{2}}dxdy^{2}+\frac{\partial^{3} f}{\partial x^{2} \partial y}dydx^{2}+2\frac{\partial^{3} f}{\partial x\partial y^{2}}dxdy^{2}+\frac{\partial^{3} f}{\partial y^{3}}dy^{3}=$$
$$\frac{\partial^{3} f}{\partial x^{3}}dx^{3}+3\frac{\partial^{3} f}{\partial x^{2}\partial y}dx^{2}dy+3\frac{\partial^{3} f}{\partial x\partial y^{2}}dxdy^{2}+\frac{\partial^{3} f}{\partial y^{3}}dy^{3}$$
Por lo tanto
$$d^{3}f=d(d^{2}f)=\frac{\partial^{3} f}{\partial x^{3}}dx^{3}+3\frac{\partial^{3} f}{\partial x^{2}\partial y}dx^{2}dy+3\frac{\partial^{3} f}{\partial x\partial y^{2}}dxdy^{2}+\frac{\partial^{3} f}{\partial y^{3}}dy^{3}$$
Diferencial de orden 3
Si $\displaystyle{d^{3}f=\frac{\partial^{3} f}{\partial x^{3}}dx^{3}+3\frac{\partial^{3} f}{\partial x^{2}\partial y}dx^{2}dy+3\frac{\partial^{3} f}{\partial x\partial y^{2}}dxdy^{2}+\frac{\partial^{3} f}{\partial y^{3}}dy^{3}}$ entonces una diferencial de orden 4 seria:
$$d^{4}f=d(d^{3}f)=\frac{\partial^{4} f}{\partial x^{4}}dx^{4}+4\frac{\partial^{4} f}{\partial x^{3}\partial y}dx^{3}dy+6\frac{\partial^{4} f}{\partial x^{2}\partial y^{2}}dx^{2}dy^{2}+4\frac{\partial^{4} f}{\partial x\partial y^{3}}dxdy^{3}+\frac{\partial^{4} f}{\partial y^{4}}dy^{4}$$
Diferencial de orden n
$$d^{n}f=\frac{\partial^{n} f}{\partial x^{n}}dx^{n}+\left(\begin{matrix}n\\1\end{matrix}\right)\frac{\partial^{n-1} f}{\partial x^{n-1}\partial y}dx^{n-1}dy+\left(\begin{matrix}n\\2\end{matrix}\right)\frac{\partial^{n-2} f}{\partial x^{n-2}\partial y^{2}}dx^{n-2}dy^{2}+\cdots+\left(\begin{matrix}n\\k\end{matrix}\right)\frac{\partial^{n-k} f}{\partial x^{n-k}\partial y^{k}}dx^{n-k}dy^{k}+\cdots+\frac{\partial^{n}f}{\partial y^{n}}dy^{n}$$
que se puede escribir
$$d^{n}f=\sum_{j=0}^{n}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n}f}{\partial x^{n-j}\partial y^{j}}dx^{n-j}dy^{j}$$
Mas adelante
Tarea Moral
1.- Aproximar el cambio de $z=6y^2-5xy+x$ cuando $(x,y)$ pasa de $(0,0)$ a $(0.5, 2.5)$
2.- Aproximar el cambio de $z=4xy$ cuando (x,y) pasa de $(1,2)$ a $(1.3, 4.2)$
3.- Usa diferenciales para calcular aproximadamente
$$A=\frac{1.02}{\sqrt{9.95}+\sqrt[3]{81}}$$
4.- Hallar el diferencial de orden 2 para $f(x,y)= 3x^2+\sqrt{xy}$
5.- Hallar el diferencial de orden 3 para $f(x,y)=sen(4x+y^2)$
