Introduccion
Análogamente al tema estudiado en cálculo de una variable respecto al criterio de la segunda derivada se analizarán, en este caso, la derivada de la derivada parcial con el objetivo de detectar máximos y mínimos de una función.
Derivadas Parciales de Orden Superior
Si $f$ es una función de doas variables $x,y$ $\Rightarrow$ $\displaystyle\frac{\partial f}{\partial x}, \displaystyle\frac{\partial f}{\partial y}$ son funciones de las mismas variables, cuando derivamos $\displaystyle\frac{\partial f}{\partial x}$ y $ \displaystyle\frac{\partial f}{\partial y}$ obtenemos las derivadas parciales de segundo orden, las derivadas de $\displaystyle\frac{\partial f}{\partial x}$ están definidas por:
$$\displaystyle\frac{\partial^{2}f}{\partial x^{2}}(x,y)=\displaystyle\lim_{h\to 0}{\displaystyle\frac{\displaystyle\frac{\partial f}{\partial x}(x+h,y)-\displaystyle\frac{\partial f}{\partial x}(x,y)}{h}}$$
$$\displaystyle\frac{\partial^{2}f}{\partial y \partial x}(x,y)=\displaystyle\lim_{k\to 0}{\displaystyle\frac{\displaystyle\frac{\partial f}{\partial x}(x,y+k)-\displaystyle\frac{\partial f}{\partial x}(x,y)}{k}}$$
Si $f$ es una función de dos variables entonces hay cuatro derivadas parciales de segundo orden.
Consideremos las diferentes notaciones para las derivadas parciales:
$$f_{1,1}=\displaystyle\frac{\partial^{2}f}{\partial x^{2}}=f_{xx}$$
$$f_{1,2}=\displaystyle\frac{\partial^{2}f}{\partial y \partial x}=\frac{\partial}{\partial y}\bigg(\frac{\partial f}{\partial x}\bigg)=f_{xy}$$
$$f_{2,1}=\displaystyle\frac{\partial^{2}f}{\partial x \partial y}=\frac{\partial}{\partial x}\bigg(\frac{\partial f}{\partial y}\bigg)=f_{yx}$$
$$f_{2,2}=\displaystyle\frac{\partial^{2}f}{\partial y^{2}}=\frac{\partial}{\partial y}\bigg(\frac{\partial f}{\partial y}\bigg)=f_{yy}$$
Ejemplo. $z=x^{3}+3x^{2}y-2x^{2}y^{2}-y^{4}+3xy$ hallar $\displaystyle\frac{\partial z}{\partial x}, \displaystyle\frac{\partial z}{\partial y},\displaystyle\frac{\partial^{2} z}{\partial x^{2}},\displaystyle\frac{\partial^{2}z}{\partial x \partial y},\displaystyle\frac{\partial^{2}z}{\partial y \partial x},\displaystyle\frac{\partial^{2} z}{\partial y^{2}}$
$$\displaystyle\frac{\partial z}{\partial x}=3x^{2}+6xy-4xy^{2}+3y$$
$$\displaystyle\frac{\partial z}{\partial y}=3x^{2}-4x^{2}y-4y^{3}+3x$$
$$\displaystyle\frac{\partial^{2} z}{\partial x^{2}}=6x+6y-4y^{2}$$
$$\displaystyle\frac{\partial^{2} z}{\partial y^{2}}=-4x^{2}-12y^{2}$$
$$\displaystyle\frac{\partial^{2}z}{\partial y \partial x}=6x-8xy+3$$
$$\displaystyle\frac{\partial^{2}z}{\partial x \partial y}=6x-8xy+3$$
Teorema 1.Teorema de schwarz
Sea $f:A\subset \mathbb{R}^{2}\rightarrow\mathbb{R}$ una función definida en el abierto A de $\mathbb{R}^{2}$. Si las derivadas parciales
$$\frac{\partial^{2} f}{\partial y\partial x}~y~\frac{\partial^{2} f}{\partial x\partial y}$$
existen y son continuas en $A$, entonces
$$\frac{\partial^{2} f}{\partial y\partial x}=\frac{\partial^{2} f}{\partial x\partial y}$$
Demostración. Sea
$\displaystyle{M=f(x+h_{1},y+h_{2})-f(x+h_{1},y)-f(x,y+h_{2})+f(x,y)}$ y definimos $$\varphi(x)=f(x,y+h_{2})-f(x,y)$$de manera que
$$\varphi(x+h_{1})-\varphi(x)=f(x+h_{1},y+h_{2})-f(x+h_{1},y)-(f(x,y+h_{2})-f(x,y))=M$$
Aplicando el TVM a $\varphi$ en el intervalo $[x,x+h_{1}]$ se tiene que existe $\theta~\in~(x,x+h_{1})$ tal que
$$\varphi(x+h_{1})-\varphi(x)=\varphi'(\theta)h_{1}$$
por otro lado
$$\varphi'(x)=\frac{\partial f}{\partial x}(x,y+h_{2})-\frac{\partial f}{\partial x}(x,y)$$
por lo tanto
$$\varphi'(\theta)=\frac{\partial f}{\partial x}(\theta,y+h_{2})-\frac{\partial f}{\partial x}(\theta,y)$$
tenemos entonces que
$$M=\varphi(x+h_{1})-\varphi(x)=\varphi'(\theta)h_{1}=\left(\frac{\partial f}{\partial x}(\theta,y+h_{2})-\frac{\partial f}{\partial x}(\theta,y)\right)h_{1}$$
Consideremos ahora $\displaystyle{\psi(y)=\frac{\partial f}{\partial x}(x,y)}$. Aplicando el TVM a $\psi$ en el intervalo $[y,y+h_{2}]$ se tiene que existe $\eta~\in~(y,y+h_{2})$ tal que
$$\psi(y+h_{2})-\psi(y)=\psi'(\eta)h_{2}$$
por otro lado
$$\psi'(y)=\frac{\partial }{\partial y}\left(\frac{\partial f}{\partial x}\right)(x,y)=\frac{\partial^{2}f}{\partial y\partial x}(x,y)$$
por lo tanto
$$\psi'(\eta)=\frac{\partial^{2}f}{\partial y\partial x}(x,\eta)$$
de esta manera
$$\psi(y+h_{2})-\psi(y)=\psi'(\eta)h_{2}=\left(\frac{\partial^{2}f}{\partial y\partial x}(x,\eta)\right)h_{2}$$
y si $\theta\in (x,x+h_{1})$ tenemos entonces que
$$\frac{\partial f}{\partial x}(\theta,y+h_{2})-\frac{\partial f}{\partial x}(\theta,y)=\left(\frac{\partial^{2}f}{\partial y\partial x}(\theta,\eta)\right)h_{2}$$
en consecuencia
$$M=\left(\frac{\partial f}{\partial x}(\theta,y+h_{2})-\frac{\partial f}{\partial x}(\theta,y)\right)h_{1}=\left(\frac{\partial^{2}f}{\partial y\partial x}(\theta,\eta)\right)h_{2}h_{1}$$
Consideremos ahora $$\overline{\varphi}(y)=f(x+h_{1},y)-f(x,y)$$de manera que
$$\overline{\varphi}(y+h_{2})-\overline{\varphi}(y)=f(x+h_{1},y+h_{2})-f(x+h_{1},y)-(f(x,y+h_{2})-f(x,y))=M$$
Aplicando el TVM a $\overline{\varphi}$ en el intervalo $[y,y+h_{2}]$ se tiene que existe $\overline{\eta}~\in~(y,y+h_{2})$ tal que
$$\overline{\varphi}(y+h_{2})-\overline{\varphi}(y)=\overline{\varphi}'(\overline{\eta})h_{2}$$
por otro lado
$$\overline{\varphi}'(y)=\frac{\partial f}{\partial y}(x+h_{1},y)-\frac{\partial f}{\partial y}(x,y)$$
por lo tanto
$$\overline{\varphi}'(\overline{\eta})=\frac{\partial f}{\partial y}(x+h_{1},\overline{\eta})-\frac{\partial f}{\partial y}(x,\overline{\eta})$$
tenemos entonces que
$$M=\overline{\varphi}(y+h_{2})-\overline{\varphi}(y)=\overline{\varphi}'(\overline{\eta})h_{2}=\left(\frac{\partial f}{\partial y}(x+h_{1},\overline{\eta})-\frac{\partial f}{\partial y}(x,\overline{\eta})\right)h_{2}$$
Consideremos ahora $\displaystyle{\overline{\psi}(x)=\frac{\partial f}{\partial y}(x,y)}$. Aplicando el TVM a $\psi$ en el intervalo $[x,x+h_{1}]$ se tiene que existe $\overline{\theta}~\in~(x,x+h_{1})$ tal que
$$\overline{\psi}(x+h_{1})-\overline{\psi}(x)=\overline{\psi}'(\overline{\theta})h_{1}$$
por otro lado
$$\overline{\psi}'(x)=\frac{\partial }{\partial x}\left(\frac{\partial f}{\partial y}\right)(x,y)=\frac{\partial^{2}f}{\partial x\partial y}(x,y)$$
por lo tanto
$$\overline{\psi}'(\overline{\theta})=\frac{\partial^{2}f}{\partial y\partial x}(\overline{\theta},y)$$
de esta manera
$$\overline{\psi}(x+h_{1})-\overline{\psi}(x)=\overline{\psi}'(\overline{\theta})h_{1}=\left(\frac{\partial^{2}f}{\partial x\partial y}(\overline{\theta},y)\right)h_{1}$$
es decir
$$\frac{\partial f}{\partial y}(x+h_{1},y)-\frac{\partial f}{\partial y}(x,y)=\left(\frac{\partial^{2}f}{\partial x\partial y}(\overline{\theta},y)\right)h_{1}$$
y si $\overline{\eta}\in (y,y+h_{2})$ tenemos entonces que
$$\frac{\partial f}{\partial y}(x+h_{1},\overline{\eta})-\frac{\partial f}{\partial y}(x,\overline{\eta})=\left(\frac{\partial^{2}f}{\partial x\partial y}(\overline{\theta},\overline{\eta})\right)h_{1}$$
en consecuencia
$$M=\left(\frac{\partial f}{\partial y}(x+h_{1},\overline{\eta})-\frac{\partial f}{\partial y}(x,\overline{\eta})\right)h_{1}h_{2}=\left(\frac{\partial^{2}f}{\partial x\partial y}(\overline{\theta},\overline{\eta})\right)h_{2}h_{1}$$
igualando ambas expresiones de M se tiene
$$\left(\frac{\partial^{2}f}{\partial y\partial x}(\theta,\eta)\right)h_{2}h_{1}=\left(\frac{\partial^{2}f}{\partial x\partial y}(\overline{\theta},\overline{\eta})\right)h_{2}h_{1}$$
donde
$$\left(\frac{\partial^{2}f}{\partial y\partial x}(\theta,\eta)\right)=\left(\frac{\partial^{2}f}{\partial x\partial y}(\overline{\theta},\overline{\eta})\right)$$
Tomando limite cuando $h_{1},h_{2}\rightarrow 0$ y usando la continuidad asumida de las parciales mixtas se tiene que $\theta,\overline{\theta}\rightarrow x$ y $\eta,\overline{\eta}\rightarrow y$ se concluye
$$\frac{\partial^{2}f}{\partial y\partial x}(x,y)=\frac{\partial^{2}f}{\partial x\partial y}(x,y)$$ $\square$
Ejemplo. Sea $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=x^{3}+3x^{2}y-2x^{2}y^{2}-y^{4}+3xy$\
En este caso
$$\frac{\partial f}{\partial x}=3x^{2}+6xy-4xy^{2}+3y$$
$$\frac{\partial f}{\partial y}=3x^{2}-4x^{2}y-4y^{3}+3x$$
$$\frac{\partial^{2} f}{\partial x^{2}}=6x+6y-4y^{2}$$
$$\frac{\partial^{2} f}{\partial y^{2}}=-4x^{2}-12y^{2}$$
$$\frac{\partial^{2} f}{\partial x\partial y}=6x-8xy+3$$
$$\frac{\partial^{2} f}{\partial y\partial x}=6x-8xy+3$$
Ejemplo. Dada la función
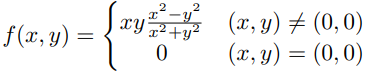
tenemos que para $(x,y)\neq (0,0)$
$$\frac{\partial f}{\partial x}=y\frac{x^{4}+4x^{2}y^{2}-y^{4}}{(x^{2}+y^{2})^{2}}$$
$$\frac{\partial f}{\partial y}=x\frac{x^{4}-4x^{2}y^{2}-y^{4}}{(x^{2}+y^{2})^{2}}$$
para el primer caso hacemos $x=0$ y tenemos
$$\frac{\partial f}{\partial x}=y\frac{x^{4}+4x^{2}y^{2}-y^{4}}{(x^{2}+y^{2})^{2}}\underbrace{=}{x=0}-y$$ para el segundo caso hacemos $y=0$ y tenemos $$\frac{\partial f}{\partial y}=x\frac{x^{4}-4x^{2}y^{2}-y^{4}}{(x^{2}+y^{2})^{2}}\underbrace{=}{y=0}1$$
Calculamos ahora
$$\frac{\partial^{2} f}{\partial y\partial x}=\frac{\partial^{2} (-y)}{\partial y\partial x}=-1$$
$$\frac{\partial^{2} f}{\partial x\partial y}=\frac{\partial^{2} (1)}{\partial x\partial y}=1$$
por lo tanto
$$\frac{\partial^{2} f}{\partial y\partial x}=-1\neq 1=\frac{\partial^{2} f}{\partial x\partial y}$$
En este caso las parciales segundas no son contiuas en $(0,0)$
Teorema. Caso General
Sea $f:A\subset\mathbb{R}^{n}\rightarrow\mathbb{R}$ definida en el abierto A de $\mathbb{R}^{n}$ tal que
$$\frac{\partial^{2} f}{\partial x_{i}\partial x_{j}}$$ sean continuas en A, entonces
$$\frac{\partial^{2} f}{\partial x_{i}\partial x_{j}}=\frac{\partial^{2} f}{\partial x_{j}\partial x_{i}}$$
Mas adelante
Tarea Moral
Determina las derivadas de segundo orden para:
1.- $f(x,y)=\dfrac{1}{x^{2}+y^{2}+1}$, $x_0=0$, $y_0=0$
2.- $f(x,y)=e^{x+y}$, $x_0=0$, $y_0=0$
3.- $f(x,y)=e^{-x^{2}-y^{2}}$, $x_0=0$, $y_0=0$
4.-$f(x,y)=sen(xy)+cos(xy)$, $x_0=0$, $y_0=0$
5.- $f(x,y)=e^{(x-1)^{2}}$, $x_0=0$, $y_0=0$
