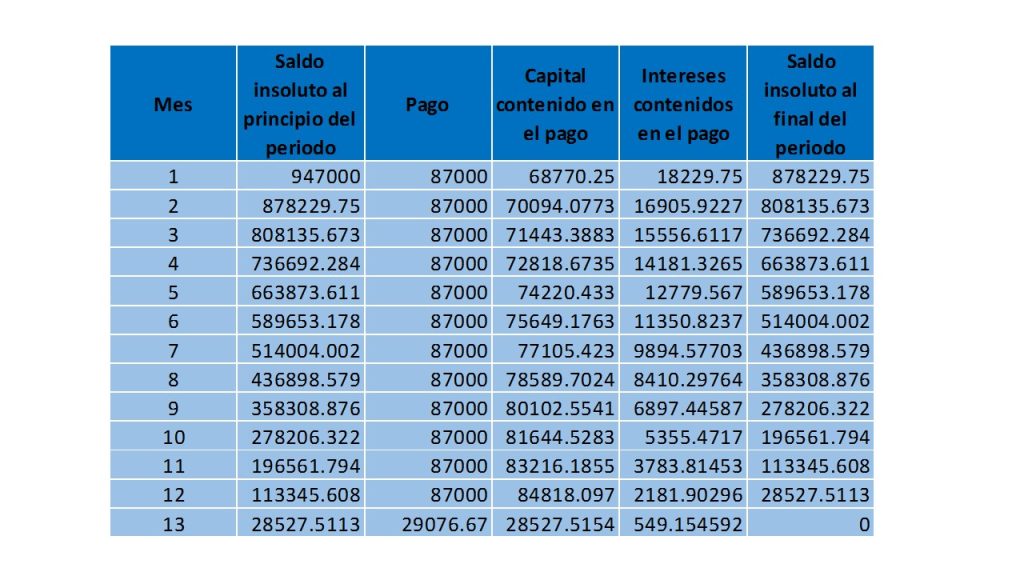
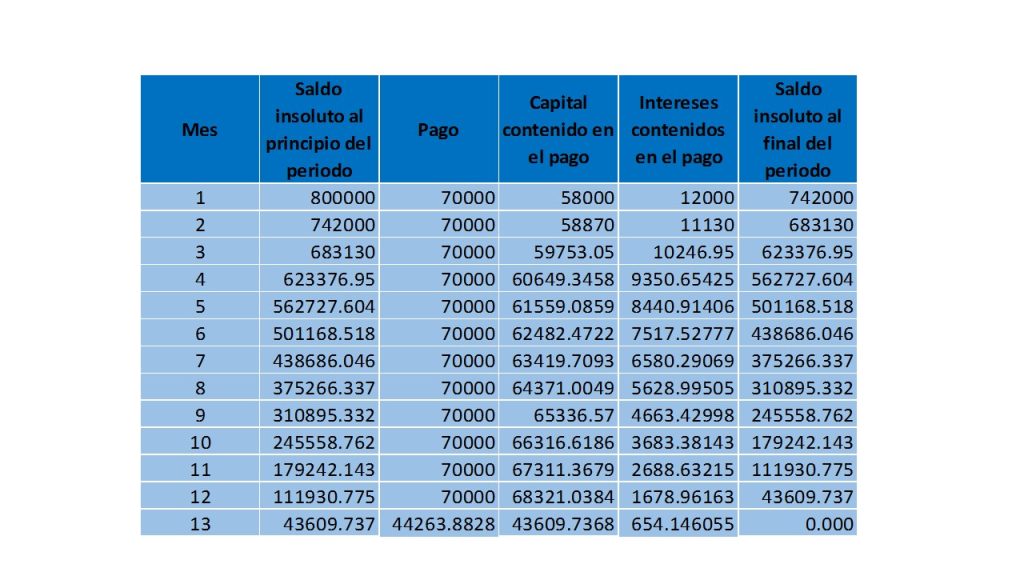
$\textcolor{Red}{\textbf{Diferenciales de funciones $f:A\subset\mathbb{R}^{2}\rightarrow\mathbb{R}$}}$

Tenemos que $f:A\subset\mathbb{R}^{2}\rightarrow\mathbb{R}$ es diferenciable si
$$f(x_{o}+h_{1},y_{0}+h_{2})=f(x_{0},y_{0})+\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}+r(h_{1},h_{2})$$
cumple
$$\lim_{(h_{1},h_{2})\rightarrow(0,0)}\frac{r(h_{1},h_{2})}{|(h_{1},h_{2})|}=0$$
Esto se puede escribir como
$$f(x_{o}+h_{1},y_{0}+h_{2})-f(x_{0},y_{0})=\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}+r(h_{1},h_{2})$$

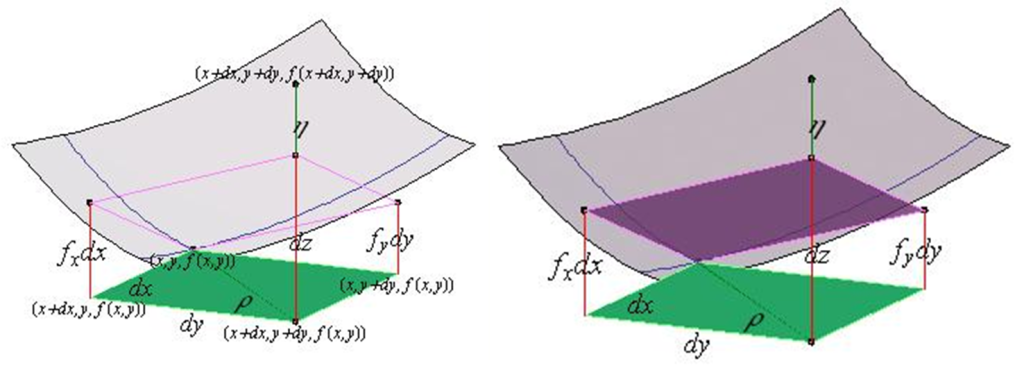
tomando
$$f(x_{o}+h_{1},y_{0}+h_{2})-f(x_{0},y_{0})=\triangle z$$
$$\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}=\frac{\partial f}{\partial x}(x_{0},y_{0})\triangle x$$
$$\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}=\frac{\partial f}{\partial y}(x_{0},y_{0})\triangle y$$
tenemos que
$$\triangle z=\frac{\partial f}{\partial x}(x_{0},y_{0})\triangle x+\frac{\partial f}{\partial y}(x_{0},y_{0})\triangle y+r(\triangle x,\triangle y)$$
haciendo $\triangle x,~\triangle y\rightarrow 0$ tenemos
$$dz=\frac{\partial f}{\partial x}(x_{0},y_{0})dx+\frac{\partial f}{\partial y}(x_{0},y_{0}) dy$$
$\textbf{Definición.}$Si $z=f(x,y)$ es una función diferenciable, la diferencial de f denotada $dz$ se define
$$dz=\frac{\partial f}{\partial x}(x_{0},y_{0})dx+\frac{\partial f}{\partial y}(x_{0},y_{0}) dy$$

$\textbf{Ejemplo.}$ Calcular la diferencial de $z=4x^{2}-xy$\En este caso
$$dz=\frac{\partial (4x^{2}-xy)}{\partial x}dx+\frac{\partial (4x^{2}-xy)}{\partial y}dy=(8x-y)dx-xdy$$

Ahora bien
$$f(x_{o}+h_{1},y_{0}+h_{2})-f(x_{0},y_{0})=\triangle z\approx \frac{\partial f}{\partial x}(x_{0},y_{0})\triangle x+\frac{\partial f}{\partial y}(x_{0},y_{0})\triangle y$$
expresa el cambio aproximado de $z=f(x,y)$ cuando $(x,y)$ pasa a $(x+\triangle x,y+\triangle y)$

$\textbf{Ejemplo.}$ Aproximar el cambio de $z=4x^{2}-xy$ cuando $(x,y)$ pasa de $(2,1)$ a $(2.1,1.5)$\
En este caso tomamos $x_{0}=2$, $y_{0}=1$, $\triangle x=0.1$ y $\triangle y=.5$ y el valor de cambio será
$$\frac{\partial f}{\partial x}(2,1)\triangle x+\frac{\partial f}{\partial y}(2,1)\triangle y=(15)(0.1)-2(0.5)=1.5$$
mientras que
$$f(2.1,1.5)-f(2,1)=14.49-14=0.49$$
por lo tanto en la aproximacion se cometió un error de $0.01$

$\textbf{Ejemplo.}$ Usando diferenciales se quiere calcular aproximadamente
$$A=\frac{0.97}{\sqrt{15.05}+\sqrt[3]{0.98}}$$

$\small{Solución.}$

Considerando la función
$$f(x,y,z)=\frac{x}{\sqrt{y+\sqrt[3]{z}}}$$
con $x=1$, $y=15$, $z=1$, $dx=-0.03$, $dy=0.05$ y $dz=-0.02$ se tiene
$$f(x+dx,y+dy,z+dz)=f(x,y,z)+df(x,y,z)$$
en este caso
$$f(x,y,z)=f(1,15,1)=\frac{1}{4}$$
$$\frac{\partial f}{\partial x}=\frac{1}{\sqrt{y}+\sqrt[3]{z}},~\frac{\partial f}{\partial y}=-\frac{x}{2}\left(y+\sqrt[3]{z}\right)^{\frac{-3}{2}},~\frac{\partial f}{\partial z}=-\frac{x}{2}(y+\sqrt[3]{z})^{\frac{-3}{2}}\frac{1}{3}z^{\frac{-2}{3}}$$
evaluando en $(1,15,1)$ se tiene
$$\frac{\partial f}{\partial x}(1,15,1)=\frac{1}{4},~\frac{\partial f}{\partial y}(1,15,1)=-\frac{1}{128},~\frac{\partial f}{\partial z}(1,15,1)=-\frac{1}{384}$$
de modo que
$$df(1,15,1)=\frac{1}{4}(-0.03)-\frac{1}{128}(0.05)-\frac{1}{384}(-0.02)=-\frac{3.01}{384}$$
por lo que
$$A=\frac{1}{4}-\frac{3.01}{384}=0.242161$$
(el valor es $0.2421726$)

$\textcolor{Red}{\textbf{Diferencial de orden 2}}$

Si $\displaystyle{df=\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy}$ entonces una diferencial de orden 2 seria:
$$d^{2}f=d(df)=d\left(\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy\right)=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy\right)dx+\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy\right)dy$$
$$=\left(\frac{\partial^{2} f}{\partial x^{2}}dx+\frac{\partial^{2} f}{\partial x\partial y}dy\right)dx+\left(\frac{\partial^{2} f}{\partial y\partial x}dx+\frac{\partial^{2} f}{\partial y^{2}}dy\right)dy=\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y\partial x}dydx+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}$$
$$=\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}$$
Por lo tanto

$$d^{2}f=d(df)=\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}$$

$\textbf{Ejemplo.}$ Hallar la diferencial de orden 2 para $f(x,y)=e^{x^{2}+y^{y}}$

$\small{Solución.}$

En este caso tenemos la fórmula
$$d^{2}f=d(df)=\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}$$
vamos a calcular las derivadas parciales correspondientes
$$\frac{\partial(e^{x^{2}+y^{2}})}{\partial x}=2xe^{x^{2}+y^{2}}$$
$$\frac{\partial(e^{x^{2}+y^{2}})}{\partial y}=2ye^{x^{2}+y^{2}}$$
$$\frac{\partial^{2}(e^{x^{2}+y^{2}})}{\partial x^{2}}=\frac{\partial}{\partial x}\left(\frac{\partial(e^{x^{2}+y^{2}})}{\partial x}\right)=\frac{\partial(2xe^{x^{2}+y^{2}})}{\partial x}=4x^{2}e^{x^{2}+y^{2}}+2e^{x^{2}+y^{2}}$$
$$\frac{\partial^{2}(e^{x^{2}+y^{2}})}{\partial y^{2}}=\frac{\partial}{\partial y}\left(\frac{\partial(e^{x^{2}+y^{2}})}{\partial y}\right)=\frac{\partial(2ye^{x^{2}+y^{2}})}{\partial y}=4y^{2}e^{x^{2}+y^{2}}+2e^{x^{2}+y^{2}}$$
$$\frac{\partial^{2}(e^{x^{2}+y^{2}})}{\partial y\partial x}=\frac{\partial}{\partial y}\left(\frac{\partial(e^{x^{2}+y^{2}})}{\partial x}\right)=\frac{\partial (2xe^{x^{2}+y^{2}})}{\partial y}=4xye^{x^{2}+y^{2}}$$
$$\frac{\partial^{2}(e^{x^{2}+y^{2}})}{\partial x\partial y}=\frac{\partial}{\partial x}\left(\frac{\partial(e^{x^{2}+y^{2}})}{\partial y}\right)=\frac{\partial (2ye^{x^{2}+y^{2}})}{\partial x}=4xye^{x^{2}+y^{2}}$$
y la diferencial de orden 2 sería:
$$d^{2}f=\left(4x^{2}e^{x^{2}+y^{2}}+2e^{x^{2}+y^{2}}\right)dx^{2}+8xye^{x^{2}+y^{2}}dxdy+\left(4y^{2}e^{x^{2}+y^{2}}+2e^{x^{2}+y^{2}}\right)dy^{2}$$

$\textcolor{Red}{\textbf{Diferencial de orden 3}}$

Si $\displaystyle{d^{2}f=\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}}$ entonces una diferencial de orden 3 seria:
$$d^{3}f=d(d^{2}f)=d\left(\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}\right)=$$
$$\frac{\partial}{\partial x}\left(\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}\right)dx+\frac{\partial}{\partial y}\left(\frac{\partial^{2} f}{\partial x^{2}}dx^{2}+2\frac{\partial^{2} f}{\partial x\partial y}dxdy+\frac{\partial^{2} f}{\partial y^{2}}dy^{2}\right)dy=$$

$$\left(\frac{\partial^{3} f}{\partial x^{3}}dx^{2}+2\frac{\partial^{3} f}{\partial x^{2}\partial y}dxdy+\frac{\partial^{3} f}{\partial x\partial y^{2}}dy^{2}\right)dx+\left(\frac{\partial^{3} f}{\partial x^{2} \partial y}dx^{2}+2\frac{\partial^{3} f}{\partial x\partial y^{2}}dxdy+\frac{\partial^{3} f}{\partial y^{3}}dy^{2}\right)dy=$$

$$\frac{\partial^{3} f}{\partial x^{3}}dx^{3}+2\frac{\partial^{3} f}{\partial x^{2}\partial y}dx^{2}dy+\frac{\partial^{3} f}{\partial x\partial y^{2}}dxdy^{2}+\frac{\partial^{3} f}{\partial x^{2} \partial y}dydx^{2}+2\frac{\partial^{3} f}{\partial x\partial y^{2}}dxdy^{2}+\frac{\partial^{3} f}{\partial y^{3}}dy^{3}=$$

$$\frac{\partial^{3} f}{\partial x^{3}}dx^{3}+3\frac{\partial^{3} f}{\partial x^{2}\partial y}dx^{2}dy+3\frac{\partial^{3} f}{\partial x\partial y^{2}}dxdy^{2}+\frac{\partial^{3} f}{\partial y^{3}}dy^{3}$$
Por lo tanto
$$d^{3}f=d(d^{2}f)=\frac{\partial^{3} f}{\partial x^{3}}dx^{3}+3\frac{\partial^{3} f}{\partial x^{2}\partial y}dx^{2}dy+3\frac{\partial^{3} f}{\partial x\partial y^{2}}dxdy^{2}+\frac{\partial^{3} f}{\partial y^{3}}dy^{3}$$

$\textcolor{Red}{\textbf{Diferencial de orden 4}}$

Si $\displaystyle{d^{3}f=\frac{\partial^{3} f}{\partial x^{3}}dx^{3}+3\frac{\partial^{3} f}{\partial x^{2}\partial y}dx^{2}dy+3\frac{\partial^{3} f}{\partial x\partial y^{2}}dxdy^{2}+\frac{\partial^{3} f}{\partial y^{3}}dy^{3}}$ entonces una diferencial de orden 4 seria:
$$d^{4}f=d(d^{3}f)=\frac{\partial^{4} f}{\partial x^{4}}dx^{4}+4\frac{\partial^{4} f}{\partial x^{3}\partial y}dx^{3}dy+6\frac{\partial^{4} f}{\partial x^{2}\partial y^{2}}dx^{2}dy^{2}+4\frac{\partial^{4} f}{\partial x\partial y^{3}}dxdy^{3}+\frac{\partial^{4} f}{\partial y^{4}}dy^{4}$$

$\textcolor{Red}{\textbf{Diferencial de orden n}}$

$$d^{n}f=\frac{\partial^{n} f}{\partial x^{n}}dx^{n}+\left(\begin{matrix}n\\1\end{matrix}\right)\frac{\partial^{n-1} f}{\partial x^{n-1}\partial y}dx^{n-1}dy+\left(\begin{matrix}n\\2\end{matrix}\right)\frac{\partial^{n-2} f}{\partial x^{n-2}\partial y^{2}}dx^{n-2}dy^{2}+\cdots+\left(\begin{matrix}n\\k\end{matrix}\right)\frac{\partial^{n-k} f}{\partial x^{n-k}\partial y^{k}}dx^{n-k}dy^{k}+\cdots+\frac{\partial^{n}f}{\partial y^{n}}dy^{n}$$

que se puede escribir
$$d^{n}f=\sum_{j=0}^{n}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n}f}{\partial x^{n-j}\partial y^{j}}dx^{n-j}dy^{j}$$

$\textcolor{Red}{\textbf{Funciones de $\mathbb{R}^{n}$ en $\mathbb{R}$}}$

$\textbf{Definición 1.}$ Una función $f:A\subset\mathbb{R}^{n}\rightarrow \mathbb{R}$ es una función $f(x_{1},x_{2},…,x_{n})$ que asocia a cada n-ada ordenada $(x_{1},x_{2},…,x_{n})$ de $\mathbb{R}^{n}$ un número real $f(x_{1},x_{2},…,x_{n})$

$\textbf{Ejemplo}$ La función $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=x^{2}+y^{2}$ asocia a dada pareja $(x,y)\in \mathbb{R}^{^{2}}$ el número real $x^{2}+y^{2}$.

$\textbf{Ejemplo}$ La función $f:\mathbb{R}^{3}\rightarrow\mathbb{R}$ dada por $f(x,y,z)=\sqrt{1-x^{2}-y^{2}-z^{2}}$ asocia a dada terna $(x,y,z)\in \mathbb{R}^{^{3}}$ el número real $\sqrt{1-x^{2}-y^{2}-z^{2}}$

$\textbf{Definición 2.}$ El $\textcolor{Red}{dominio}$ de una función $f:A\subset \mathbb{R}^{n}\rightarrow \mathbb{R}$ es el conjunto
$$Dom_{f}\left\{(x_{1},x_{2},…,x_{n})\in\mathbb{R}^{n}~|~f(x_{1},x_{2},…,x_{n})\in\mathbb{R}\right\}$$

$\textbf{Ejemplo}$ La función $f:\mathbb{R}^{3}\rightarrow\mathbb{R}$ dada por $f(x,y,z)=\sqrt{1-x^{2}-y^{2}-z^{2}}$ asocia a dada terna $(x,y,z)\in \mathbb{R}^{^{3}}$ el número real $\sqrt{1-x^{2}-y^{2}-z^{2}}$ tiene como dominio el conjunto

$$Dom_{f}=\left\{(x,y,z)\in\mathbb{R}^{3}~|~1-x^{2}-y^{2}-z^{2}\geq0 \right\}=\left\{(x,y,z)\in\mathbb{R}^{3}~|~1\geq x^{2}+y^{2}+z^{2}\right\}$$

$\textbf{Ejemplo}$ La función $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=x^{2}+y^{2}$ asocia a dada pareja $(x,y)\in \mathbb{R}^{^{2}}$ el número real $x^{2}+y^{2}$ en este caso el dominio es $\mathbb{R}^{2}$

$\textbf{Definición 3.}$ El $\textcolor{Red}{rango}$ de una función $f:A\subset\mathbb{R}^{n}\rightarrow \mathbb{R}$ es el conjunto
$$Ran_{f}= \left\{f(x_{1},x_{2},…,x_{n})\in\mathbb{R}~|~(x_{1},x_{2},…,x_{n})\in\mathbb{R}^{n} \right\}$$

$\textbf{Ejemplo}$ La función $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=\sqrt{1-x^{2}-y^{2}}$ asocia a dada pareja $(x,y)\in \mathbb{R}^{^{2}}$ el número real $\sqrt{1-x^{2}-y^{2}}$ en este caso el rango de la función es el conjunto
$$\left\{z\in\mathbb{R}~|~0\leq z\leq1 \right\}$$

$\textbf{Definición 4.}$ La $\textcolor{Red}{gráfica}$ de una función $f:A\subset\mathbb{R}^{n}\rightarrow \mathbb{R}$ es el conjunto
$$Gra_{f}=\left\{(x_{1},x_{2},…,x_{n},f(x_{1},x_{2},…,x_{n}))\in\mathbb{R}^{n+1}~|~(x_{1},x_{2},…,x_{n})\in\mathbb{R}^{n}\right\}$$

$\textbf{Ejemplo}$ La gráfica de la función $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=x^{2}+y^{2}$ es un paraboloide cuyo aspecto es

$\textbf{Ejemplo}$ La gráfica de la función $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=x^{2}-y^{2}$ es un paraboloide hiperbolico (silla de montar) cuyo aspecto es

$\textcolor{Red}{\textbf{Conjuntos de Nivel}}$

$\textbf{Definición 5.}$ Sea $f:\mathbb{R}^{n}\rightarrow\mathbb{R}$ y sea $c\in\mathbb{R}$. El conjunto de nivel del valor c se define como:
$$C_{N}=\left\{x\in\mathbb{R}^{n}~|~f(x)=c\right\}$$

$\textbf{Ejemplo}$ Describir el conjunto de nivel de la función $f(x,y)=x^{2}+y^{2}$

$Solución$ En este caso el conjnuto de nivel es$$C_{N}=\left\{(x,y)\in\mathbb{R}^{2}~|~x^{2}+y^{2}=c\right\}$$
geometricamente son circunferencias con centro el origen y radio $c$.

$\textbf{Ejemplo}$ Describir el conjunto de nivel de la función $f(x,y)=x^{2}-y^{2}$

$Solución$ En este caso el conjnuto de nivel es$$C_{N}={(x,y)\in\mathbb{R}^{2}~|~x^{2}-y^{2}=c}$$
geometricamente son circunferencias con centro el origen y radio c

$\textbf{Ejemplo}$ La función $f:\mathbb{R}^{2}\rightarrow \mathbb{R}$ dada por $f(x,y)=x^{2}+y^{2}$ tiene como gráfica el paraboloide de revolución $z=x^{2}+y^{2}$

Las curvas de nivel son: el vacio para $a<0$, y para $a>0$ es el conjunto $$\left\{(x,y)\in \mathbb{R}^{2}|x^{2}+y^{2}=a\right\}$$, es decir un círculo de radio $\sqrt{a}$ con centro en el origen

$\textbf{Ejemplo}$ La función $f:\mathbb{R}^{2}\rightarrow \mathbb{R}$ dada por $f(x,y)=x^{2}-y^{2}$ tiene como gráfica el paraboloide hiperbolico $z=x^{2}-y^{2}$

Las curvas de nivel son: para $a=0\Rightarrow x^2-y^2=0$ par de rectas que se cortan en el origen, y para $a=1\Rightarrow x^2-y^2 =1$ es una hiperbola paralela al eje X que lo corta en $(\pm 1,0)$, para $a=-1\Rightarrow x^2-y^2=-1$ es una hiperbola paralela al eje Y y que lo corta en $(0,\pm 1)$

$\textbf{Ejemplo}$ La función $f:\mathbb{R}^{3}\rightarrow \mathbb{R}$ dada por $f(x,y,z)=\sqrt{x^{2}+y^{2}+z^2}$ tiene el siguiente conjunto de nivel
$${(x,y,z)\in \mathbb{R}^{3}|\sqrt{x^2+y^2+z^2}=a}$$

Las superficies de nivel son: para $a=0\Rightarrow \sqrt{x^2+y^2+z^2}=0$ el origen, y para $a=1\Rightarrow \sqrt{x^2+y^2+z^2}=1$ es una esfera, $a=2\Rightarrow \sqrt{x^2+y^2+z^2}=2$ es una esfera

La función $f:\mathbb{R}^{3}\rightarrow \mathbb{R}$ dada por $f(x,y,z)=x^{2}-y^{2}+z^2$ tiene el siguiente conjunto de nivel
$$\left\{(x,y,z)\in \mathbb{R}^{3}|x^2-y^2+z^2=a\right\}$$

Las superficies de nivel son: para $a=0\Rightarrow x^2-y^2+z^2=1$ es un hiperboloide de un manto, y para $a=1\Rightarrow x^2-y^2+z^2=1$ es un hiperboloide de un manto, $a=2\Rightarrow \sqrt{x^2-y^2+z^2}=2$ es un hiperboloide de un manto

$\textcolor{Red}{\textbf{Límite de Funciones de $\mathbb{R}^{n} \rightarrow \mathbb{R}$}}$

Sea $f:\Omega\subset\mathbb{R}^{n} \rightarrow \mathbb{R}$, y sea $x_{0}$ un punto de acumulación de $\Omega$. Se dice que $L\in\mathbb{R}$ es el límite de $f$ en
$x_{0}$, y se denota por: $$\displaystyle\lim_{x\rightarrow x_{0}}f(x)=L$$ Si dado $\varepsilon > 0$, existe $\delta > 0$ tal que $|f(x)-b|<\varepsilon$ cuando $x \in \Omega$, $0<|x-x_{0}|<\delta$

$\small{Observación:}$ Es necesarío que $x_{0}$ sea punto de acumulacion de $\Omega$.Usando la definición de límite, demostrar que:
$$\displaystyle\lim_{(x,y) \rightarrow (0,0)}\frac{x^{4}y^{2}}{(x^{2}+y^{2})^{2}}=0$$
Por demostrar, para todo $\varepsilon > 0$ existe $\delta >
0$ tal que $0 < |(x,y) – (0,0)| < \delta$ entonces $\displaystyle\left| \frac{x^{4}y^{2}}{(x^{2}+y^{2})^{2}} \right| < \varepsilon$ como $x^{2} \leq x^{2}+y^{2}$ entonces $x^{4} \leq (x^{2}+y^{2})^{2}$ entonces $\displaystyle\frac{1}{(x^{2}+y^{2})^{2}} \underset{(*)}{\leq} \displaystyle\frac{1}{x^{4}}$

$\therefore$ $\displaystyle\left|\frac{x^{4}y^{2}}{(x^{2}+y^{2})^{2}}\right| \underset{(*)}{\leq}
\displaystyle\left|\frac{x^{4}y^{2}}{x^{4}}\right| \leq |y^{2}|=y^{2}\leq (\sqrt{x^{2}+y^{2}})^{2} <
\delta^{2}$

$\therefore$ Si $\delta^{2}=\varepsilon$ entonces $\delta=\sqrt{\varepsilon}$

Introducción

En ésta sección, se continua analizando otro tipo de anualidades y la forma en que se puede construir su respectiva tabla de amortización, considerando el caso, en el que algunas empresas, de acuerdo con su experiencia, tienen contemplado el ingreso de recursos extras, a lo largo del año.

Concepto y construcción

En la sección donde se abordo el tema de anualidades, hubo algunos casos en donde se otorgaba un crédito en el que la forma de pagarlo, el acreditado realizaba pagos en el año, pero al final de éste agregaba más pagos, ya que por ejemplo, consideraba recursos que podía tener, por concepto de aguinaldo, prestaciones, cajas de ahorro, por mencionar algunas. Para este tipo de situaciones, la tabla de amortización que puede representar el comportamiento de los pagos de dicho crédito, en general es semejante el proceso de construcción que hasta este momento se ha estado utilizando. Con la diferencia radica en la forma en que se hacen los registros de éstos pagos extras, los cuales también se harán en un mismo periodo.

Por ejemplo: Se otorga un crédito hipotecario a una empresa de refresco, la cual quiere modernizar su planta de producción, la cantidad de dicho crédito asciende a \$445,000 , para pagar en un lapso de tiempo de 3 años, mediante 12 trimestres en los que se hará un pago de \$33,573.45, los días 20 del mes. Posterior a ése tiempo, se realizarán pagos anuales por la cantidad de \$60,000 a partir del mes de diciembre.

El contrato en cuestión, entra en operación el día 20 de marzo del año 2021, acordando una tasa de interés de 4.4% fija efectiva trimestral, la cual aplicará durante toda la duración del crédito. Los pagos se realizarán en forma vencida, por lo que el primer pago se tendrá que hacer el día 20 de junio del 2021.

La ecuación de valor que se usará para resolver este problema es la siguiente:

$$445,000=X\prescript{}{12}{\mathbf{A}}_{0.044}+60,000\prescript{}{3}{\mathbf{\ddot{A}}}_{0.18342}v_{0.043}^3;$$

de donde $X=\$33,573.45$

A continuación se muestra la tabla de amortización en la que se agregó una columna, en la que se anotara las fechas en las que se realizaran los pagos. Observe que hay dos columnas para el registro de las fechas de los pagos una que corresponde a los pagos trimestrales, y otra para los pagos anuales, los cuales son pagos que se recibirán al final de año, por concepto de los aguinaldos que en dichas fechas recibe.

Tabla de amortización de N pagos iguales y uno desigual

Este tipo de amortización ocurre, en los casos que la empresa que solicita el crédito pacta que la cantidad de los pagos es ajustada a su posibilidad de pago, en lugar de aceptar la que ofrece la institución que otorga el crédito. En estos casos se hace uso del concepto de anualidades tomando la cantidad que propone el deudor, y la variable n la cual va a representar el número de pagos, para conocer su valor será despejada de la ecuación de valor. Como la cantidad propuesta por el deudor, puede que no tenga considerados pagos completos para cubrir el pago total del préstamo, es por esta razón que se recurre al pago desigual, con el que será liquidado por completo en el último pago, la deuda. Para poder conocer la cantidad a la asciende éste pago desigual, será obtenido a partir de una segunda ecuación de valor, basada en la original, donde ya se conocen la cantidad de pagos completos.

La construcción de la amortización, sigue compartiendo muchas similitudes a como se han venido elaborando en los temas anteriores, con la diferencia de que el último pago es diferente.

Por ejemplo: una empresa le otorgan un crédito de \$947,000, y de los recursos que tiene por concepto de ingresos, puede disponer de la cantidad \$87,000 de forma mensual, los cuales serán destinado al pago de dicho crédito. La tasa de interés que acordaron fue del 23.1% convertible mensualmente. Para resolver éste problema, la ecuación de valor que se va a utilizar es la siguiente:

$$947,000=87,000\prescript{}{n}{\mathbf{A}}_{0.01925}$$

recordemos que el valor 0.01925, se obtiene porque se está trabajando con una tasa convertible mensual, por lo que se hace lo siguiente para poder ocuparla:

$$\frac{23.1}{12}=1.925$$

$$\frac{1.925}{100}=0.01925$$

para obtener el valor de n, se hace lo siguiente:

$$947,000=87,000\left(\frac{1-v_{0.01925}^n}{0.01925}\right)$$

$$947,000=87,000\left(\frac{1-\left(\frac{1}{(1+0.01925)^n}\right)}{0.01925}\right)$$

$$\frac{947,00}{87,000}=\left(\frac{1-\left(\frac{1}{(1+0.01925)^n}\right)}{0.01925}\right)$$

$$10.88505747=\left(\frac{1-\left(\frac{1}{(1+0.01925)^n}\right)}{0.01925}\right)$$

$$(0.01925)(10.88505747)=1-\left(\frac{1}{(1+0.01925)^n}\right)$$

$$(-1)(0.2095373563-1)=(-1)\left(-\left(\frac{1}{(1+0.01925)^n}\right)\right)$$

$$1-0.2095373563=\left(\frac{1}{(1+0.01925)^n}\right)$$

$$0.7904626437=\frac{1}{(1+0.01925)^n}$$

$$(0.7904626437)(1.01925)^n=1$$

$$(1.01925)^n=\frac{1}{0.7904626437}=1.265081921$$

$$(n)(log(1.01925))=log(1.265081921)$$

$$n=\frac{log(1.265081921)}{log(1.01925)}=12.332222$$

de dicha ecuación se nos arroja el valor de n=12.332222, lo cual se interpreta como 12 pagos por la cantidad de \$870,000 con un pago desigual, dando un total de 13 pagos. El valor del último pago, se obtiene con la siguiente ecuación:

$$947,000=87,000\prescript{}{12}{\mathbf{A}}_{0.01925}+Xv_{0.1925}^13$$

$$947,000=87,000\left(\frac{1-v_{0.01925}^12}{0.01925}\right)+Xv_{0.01925}^{13}$$

$$947,000=87,000\left(\frac{1-\left(\frac{1}{(1+0.01925)^{12}}\right)}{0.01925}\right)+X\left(\frac{1}{(1+0.01925)^{13}}\right)$$

$$947,000=87,000(10.62421639)+X(10.7804599799)$$

despejando X:

$$X=\frac{22,693.17405}{0.7804599799}$$

se obtiene el valor que estamos buscando: X=29,076.67.

A continuación se muestra la tabla de amortización:

Ejercicios resueltos

Ejercicio. La empresa de refacciones de maquilas, quiere ampliar su planta productora, para lograrlo solicito un crédito por la cantidad de \$800,000 pesos, y de acuerdo a su experiencia de ingresos anuales, puede disponer de la cantidad de \$70 mil pesos, para hacer pagos de forma mensual, con una tasa de interés convertible bimestral del 18%. El dueño de la empresa quiere saber: ¿Cuántos pagos tendría que hacer para liquidar totalmente la deuda? y también quiere conocer su tabla de amortización.

Más adelante…

Se continuara, un poco más, abordando algunas variantes de construcción de las tablas de amortización, y ejemplificando algunas situaciones en las que se aplican, describiendo el contexto para su mejor comprensión.

• Matemáticas Financieras
• Entrada anterior
• Entrada siguiente

$\textbf{Definición}$Una sucesión en $\mathbb{R}^{n}$ es cualquier lista infinita de vectores en $\mathbb{R}^{n}$ $\overline{x_{1}},\overline{x_{2}},…,\overline{x_{k}},…$ algunos de los cuales o todos ellos pueden coincidir entre si. Dada una sucesión $\overline{x_{1}},\overline{x_{2}},…,\overline{x_{k}},…$ se define de manera natural una función de los enteros positivos $\mathbb{N}$ en $\mathbb{R}^{n}$ tal que a cada entero positivo $k$ se le asigna un vector $\overline{x_{k}}\in \mathbb{R}^{n}$
A la colección ordenada de los elementos de una sucesión la denotaremos

$$\left\{ \overline{x}_{k}\right\} _{k=1}^{\infty },\left\{\overline{x}_{k}\right\}$$

$\textbf{Ejemplos}$ Considerando el espacio $\mathbb{R}^{2}$ sea la sucesión $\left\{\overline{x_{k}}\right\}_{k=1}^{\infty}$ dada por $\overline{x_{k}}=\left(k,\frac{1}{k}\right)$ cuyos elementos podemos listar como sigue:

$$\left\{(1,1),\left(2,\frac{1}{2}\right),\left(3,\frac{1}{3}\right),…\right\}$$

Considerando la sucesión $\left\{\overline{x_{k}}\right\}\in \mathbb{R}^{n}$. Cada vector $\overline{x_{k}}\in \left\{\overline{x_{k}}\right\}$ esta dado de la siguiente manera:

$$\overline{x_{k}}=\left(x_{1,k},x_{2,k},…,x_{n,k}\right)$$

Es decir, dicho vector define de manera natural $n$ sucesiones $\left\{\overline{x}\right\}$ en $\mathbb{R}$ , las cuales, llamaremos sucesiones componentes o sucesiones proyección, así, la primera sucesión componente del ejemplo anterior es: $\left\{x_{1,k}\right\}=k$ y la segunda sucesión proyección del ejemplo anterior es $\left\{x_{2,k}\right\}=\frac{1}{k}$

$\textbf{Ejemplo}$ Sea la sucesión $\left\{\overline{x_{k}}\right\}_{k=1}^{\infty}$ dada por $\overline{x_{k}}=\left(\frac{k+1}{k+2},\frac{1}{2^{k}}\right)$ cuyas sucesiones componentes son:

$$\overline{x_{1_{k}}}=\left(\frac{k+1}{k+2}\right)\quad \overline{x_{2_{k}}}=\left(\frac{1}{2^{k}}\right)$$

$\textbf{Ejemplo}$ Sea la sucesión $\left\{\overline{x_{k}}\right\}_{1}^{\infty}$ dada por $\overline{x_{k}}=\left(\left(1+\frac{1}{k}\right)^{k},\sqrt[k]{k},\sqrt[k]{\frac{1}{k}}\right)$ cuyas sucesiones componentes son:

$$\overline{x_{1_{k}}}=\left(1+\frac{1}{k}\right)^{k}\quad \overline{x_{2_{k}}}=\sqrt[k]{k}\quad \overline{x_{3_{k}}}=\sqrt[k]{\frac{1}{k}}$$

$\textcolor{Red}{\textbf{Convergencia de Sucesiones en $\mathbb{R}^{n}$}}$

$\textbf{Definición.}$ Una sucesión $\left\{\overline{x_{k}}\right\}_{k=1}^{\infty}$ en $\mathbb{R}^{n}$ se dice que converge a un vector $\overline{x}$ en $\mathbb{R}^{n}$ si $$\forall\quad \epsilon>0\quad \exists\quad N_{0}\in\mathbb{N}\quad tal\quad que \quad |\overline{x_{k}}-\overline{x}|<\epsilon\quad \forall k>N_{0}$$
En este caso diremos que la sucesión es convergente y que $\overline{x}$ es el limite de la sucesión y escribimos $$\lim_{k\rightarrow\infty}\overline{x_{k}}=\overline{x}$$

$\textbf{Proposición.}$ Unicidad del Limite: Consideremos una sucesión $\left\{\overline{x_{k}}\right\}_{k=1}^{\infty}$ en $\mathbb{R}^{n}$ y sean $\overline{x},\overline{y}\in \mathbb{R}^{n}$ tal que $$\overline{x}=\lim_{k\rightarrow\infty}\overline{x_{k}}\quad y \quad \overline{y}=\lim_{k\rightarrow\infty}\overline{x_{k}}$$ entonces $\overline{x}=\overline{y}$

$\small{Demostración}$ Supongamos que $\overline{x}\neq\overline{y}$ y tomemos $\epsilon=\frac{1}{2}|\overline{x}-\overline{y}|>0$.Por definición $\overline{x}=\lim_{k\rightarrow\infty}\overline{x_{k}}$ por lo que $\exists N_{0_{x}} \in \mathbb{N}$ tal que $|\overline{x_{k}}-\overline{x}|<\epsilon$ para $k>N_{0_{x}}$ y analogamente se tiene que $\overline{y}=\lim_{k\rightarrow\infty}\overline{x_{k}}$ por lo que $\exists N_{0_{y}} \in \mathbb{N}$ tal que $|\overline{x_{k}}-\overline{y}|<\epsilon$ para $k>N_{0_{y}}$. Sea ahora $N_{0}=m\acute{a}x\left\{N_{0_{x}},N_{0_{y}}\right\}$ entonces se cumple simultaneamente que $|\overline{x_{k}}-\overline{x}|<\epsilon$ y $|\overline{x_{k}}-\overline{y}|<\epsilon$ para $k>N_{0}$ $\therefore$ $$|\overline{x}-\overline{y}|=|\overline{x}-\overline{x_{k}}+\overline{x_{k}}-\overline{y}|\leq |\overline{x}-\overline{x_{k}}|+|\overline{x_{k}}-\overline{y}|<2\epsilon=2\left(\frac{1}{2}|\overline{x}-\overline{y}|\right)=|\overline{x}-\overline{y}|(falso)$$ $\square$

$\textbf{Proposición.}$ Sea $\left\{\overline{x_{k}}\right\}_{k=1}^{\infty}$ una sucesión en $\mathbb{R}^{n}$ y sean $${\overline{x_{1_{k}}}}_{1}^{\infty}=(x_{1_{1}},x_{1_{2}},…)$$ $${\overline{x_{2_{k}}}}_{1}^{\infty}=(x_{2_{1}},x_{2_{2}},…)$$ $$\vdots$$ $${\overline{x_{n_{k}}}}_{1}^{\infty}=(x_{n_{1}},x_{n_{2}},…)$$ las sucesiones componentes de la sucesión ${\overline{x_{k}}}_{1}^{\infty}$. Entonces la sucesión ${\overline{x_{k}}}_{1}^{\infty}$ converge a $\overline{x}=(x_{1},x_{2},…)$ en $\mathbb{R}^{n}$ si y solo si para cada $j=1,2,…$ se tiene que $x_{n_{j}}$ converge a $x_{j}$.

$\small{Demostración.}$ Supóngase que la sucesión $\left\{\overline{x_{k}}\right\}_{k=1}^{\infty}$ converge a $\overline{x}=(x_{1},x_{2},…)$ esto quiere decir que $\exists N_{0}\in \mathbb{N}$ tal que $|\overline{x_{k}}-\overline{x}|<\epsilon$ para $k>N_{0}$ y dado que $$0\leq|x_{j_{k}}-x_{j}|\leq|\overline{x_{k}}-\overline{x}|<\epsilon$$ entonces se tiene que $$0\leq|x_{j_{k}}-x_{j}|<\epsilon$$ lo que significa que $$\lim_{k\rightarrow\infty}x_{j_{k}}=x_{j}$$
Reciprocamente, supongamos que para cada j $$\lim_{k\rightarrow\infty}x_{j_{k}}=x_{j}$$ lo que significa que
$$|x_{j_{k}}-x_{j}|<\frac{\epsilon}{n}$$
$$\therefore\quad 0\leq|\overline{x_{k}}-\overline{x}|\leq |x_{1_{k}}-x_{1}|+|x_{2_{k}}-x_{2}|+…+|x_{n_{k}}-x_{n}|<\frac{\epsilon}{n}+\frac{\epsilon}{n}+…+\frac{\epsilon}{n}=\epsilon$$
$$\therefore \quad \lim_{k\rightarrow\infty}\overline{x_{j_{k}}}=\overline{x}$$

$\square$

$\textbf{Ejemplo.}$

Consideremos la sucesión $\overline{x_{k}}=\left(\frac{1}{k},\frac{k}{k+1}\right)$ tenemos que $$\lim_{k\rightarrow\infty}\overline{x_{1_{k}}}=\lim_{k\rightarrow\infty}\frac{1}{k}=0$$ $$\lim_{k\rightarrow\infty}\overline{x_{2_{k}}}=\lim_{k\rightarrow\infty}\frac{k}{k+1}= \lim_{k\rightarrow\infty}\frac{\frac{k}{k}}{\frac{k}{k}+\frac{1}{k}}=\lim_{k\rightarrow\infty}\frac{1}{1+\frac{1}{k}}=1$$
$\therefore$ $\lim_{k\rightarrow\infty}\overline{x_{k}}=(0,1)=\overline{x}$

Ahora para comprobarlo tenemos que $$\left\|\overline{x_{k}}-\overline{x}\right\|=\left\|\left(\frac{1}{k},\frac{k}{k+1}\right)-(0,1)\right\|=\sqrt{\frac{1}{k^{2}}+\left(\frac{k}{k+1}-1\right)^{2}}=\sqrt{\frac{1}{k^{2}}+\frac{1}{(k+1)^{2}}}<\sqrt{\frac{2}{k^{2}}}=\frac{\sqrt{2}}{k}$$ $$\therefore\quad \frac{\sqrt{2}}{k}<\epsilon\Leftrightarrow \frac{\sqrt{2}}{\epsilon}N_{0}\therefore \quad \left|\left(\frac{1}{k},\frac{k}{k+1}\right)-(0,1)\right|<\epsilon$$

$\textbf{Definición.}$ Deciimos que $A\subset \mathbb{R}^{n}$ es un conjunto acotado si y solo si $\exists M>0$ tal que $\forall \overline{a}\in A$ se cumple $|\overline{a}|\leq M$

$\textbf{Proposición.}$ Sea $\left\{\overline{x}_{k}\right\}\subset \mathbb{R}^{n}$, si $\left\{\overline{x}_{k}\right\}$ converge, entonces $\left\{\overline{x}_{k}\right\}$ es acotada.

Si $\left\{\overline{x}_{k}\right\}$ converge entonces $\lim_{k\rightarrow \infty}\overline{x}_{k}=\overline{x}\Rightarrow \lim_{k\rightarrow \infty}x_{k,j}=x_{j} \forall j=1,…,n$ por lo tanto se tiene que $\left\{x_{k,j}\right\}$ es acotada y por tanto $\exists M_{j}>0$ tal que $|x_{k,j}|\leq M_{j}$ $\forall k$ $\therefore$ se tiene que $$\left\|\overline{x_{k}}\right\|\leq|x_{1,k}|+|x_{2,k}|+\cdot\cdot\cdot+|x_{n,k}|\leq n\cdot \max\left\{x_{k,j}\right\}=n \cdot M_{j}=M$$ $\therefore \left\{\overline{x}_{k}\right\}$ es acotada.

$\square$

$\textbf{Teorema}$ Un subconjunto $A\subset \mathbb{R}^{n}$ es cerrado si y solo si contiene a todos sus puntos de acumulación.

$\small{Demostración.}$ ( $\Rightarrow$ ) Suponemos que A es cerrado. Sea $\overline{x}$ un punto de acumulación de A y suponemos que $\overline{x}\notin A$. Como $A^{c}$ es abierto y $\overline{x}\in A^{c}$ existe $r>0$ tal que $B(\overline{x},r)\subset A^{c}$ $\therefore$ $B(\overline{x},r)\cap A=\emptyset$ $\nabla$ pues $\overline{x}$ es punto de acumulaión de A.

( $\Leftarrow$ ) Supongamos que A contiene a todos sus puntos de acumulación. Sea $U=A^{c}$ queremos probar que $U$ es abierto. Sea $\overline{x}\in U$ como $\overline{x}$ no es de acumulación $\exists r>0$ tal que $B(\overline{x},r)\cap A=\emptyset$ $\therefore$ $B(\overline{x},r)\subset A^{c}$ $\therefore$ $A^{c}$ es abierto. $\square$

$\textbf{Teorema.}$ Sea $A\subset \mathbb{R}^{n}$ y $\overline{x}\in \mathbb{R}^{n}$. Entonces, $\overline{x}$ es un punto de acumulación de $A$ si y solo si $\exists\left\{\overline{x}_{k}\right\}\in A$ con $\overline{x_{k}}\neq \overline{x}$ $\forall k$ tal que $\overline{x}_{k}\rightarrow \overline{x}$$

$\small{Demostración.}$ Suponemos que $\overline{x}$ es punto de acumulación de $A$ entonces para cada $k \in \mathbb{N}$ $\exists$ $\overline{x_{k}}\in A\cap B(\overline{x},\frac{1}{k})$ con $\overline{x_{k}}\neq \overline{x}$ $\therefore$ $\overline{x_{k}}\rightarrow \overline{x}$
$\textcolor{Red}{\Leftarrow}$ Sea $B(\overline{x},r)$ como $\overline{x_{k}}\rightarrow \overline{x}$ $\exists k_{0}\in\mathbb{N}$ tal que $\overline{x_{k}}\in B(\overline{x},r)$ $\forall k>k_{0}$ $\therefore$ $\exists$ $\overline{x_{k}}\in A\cap B(\overline{x},r)$ $\therefore$ $\overline{x}$ es punto de acumulación. $\square$

$\textcolor{Red}{\textbf{Criterio de Convergencia de Cauchy}}$

$\textbf{Definición.-}$ Sea ${\overline{x_{k}}}$ una sucesión de puntos de $\mathbb{R}^{n}$. Se dice que ${\overline{x_{k}}}$ es una sucesión de Cauchy si dado $\epsilon>0$ $\exists N_{0}\in \mathbb{N}$ tal que $|\overline{x_{k}}-\overline{x_{l}}|<\epsilon$ $\forall k,l\geq N_{0}$

$\textbf{Teorema.-}$ Una sucesión $\overline{x_{k}}\in \mathbb{R}^{n}$ es convergente si y solo si cumple el criterio de Cauchy

$Demostración$ $\textcolor{Red}{\Rightarrow}$ Suponemos que ${\overline{x_{k}}}\rightarrow \overline{x}$ $\therefore$ $|\overline{x_{k}}-\overline{x}|<\epsilon$ $\forall k>N_{0}$. Se tiene entonces que $$|\overline{x_{k}}-\overline{x_{l}}|=|\overline{x_{k}}-\overline{x}+\overline{x}-\overline{x_{l}}|\leq |\overline{x_{k}}-\overline{x}|+|\overline{x}-\overline{x_{l}}|<\frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon$$ $\forall k,l>N_{0}$ $\therefore$ $\left\{\overline{x_{k}}\right\}$ es convergente. $\square$