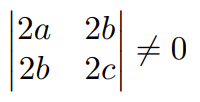$\textcolor{Red}{\textbf{Diferenciabilidad de Funciones de $\mathbb{R}^{2}\rightarrow \mathbb{R}$}}$

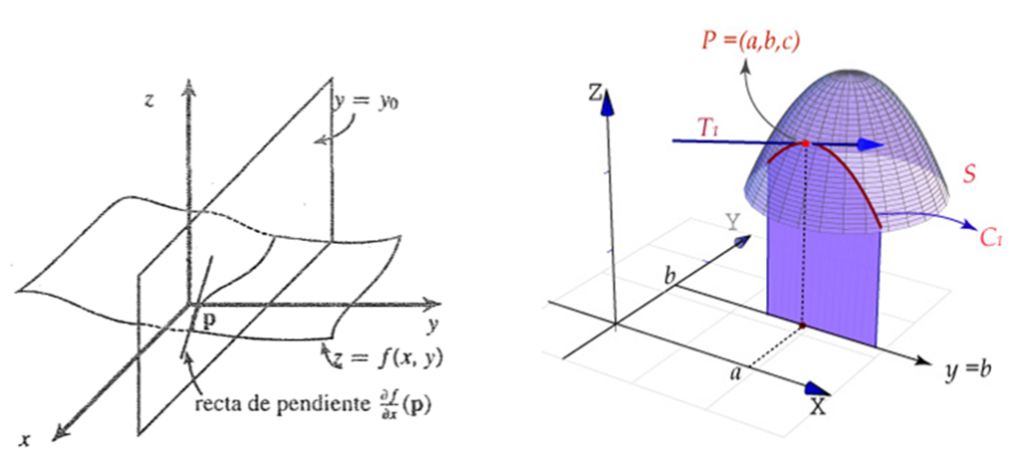
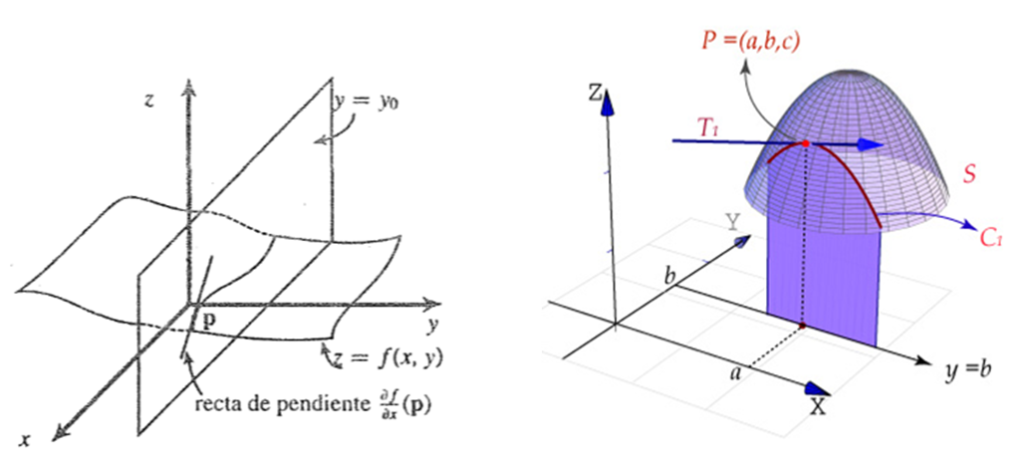
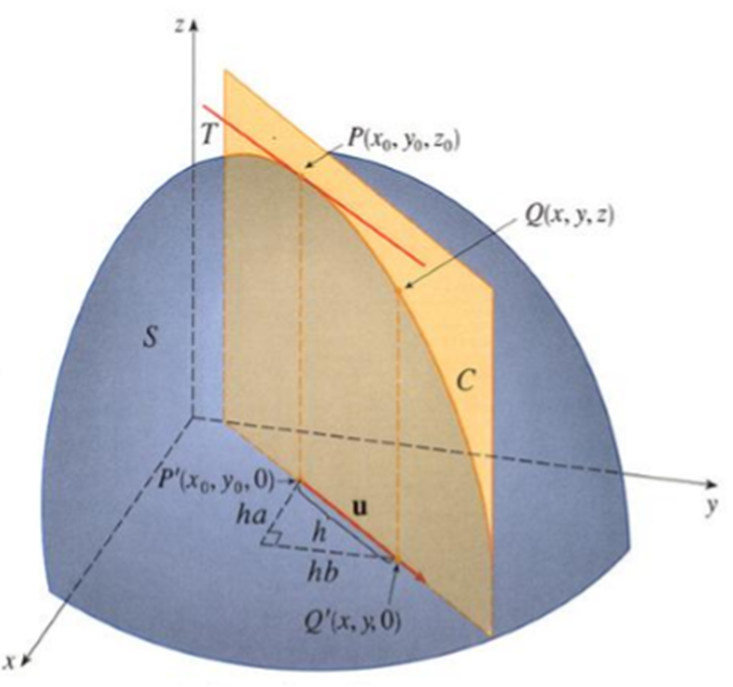
$\textbf{Definición.}$ Sea $A\subset\mathbb{R}^{2}$, un abierto, $f:A\rightarrow\mathbb{R}$ y $(x_{0},y_{0})\in A$. Se dice que f es diferenciable en $(x_{0},y_{0})$ si existen las derivadas parciales $\displaystyle{\frac{\partial f}{\partial x}(x_{0},y_{0}),~~\frac{\partial f}{\partial y}}(x_{0},y_{0})$ tal que
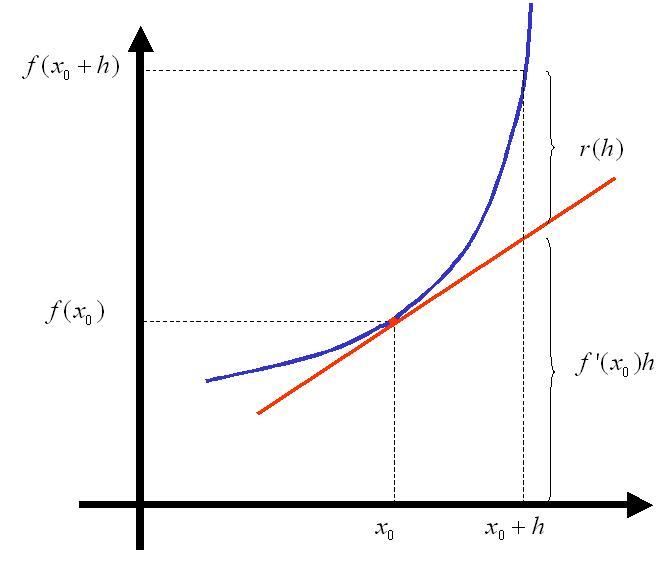
$$f((x_{0},y_{0})+(h_{1},h_{2}))=f(x_{0},y_{0})+\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}+r(h_{1},h_{2})$$donde
$$\lim_{(h_{1},h_{2})\rightarrow(0,0)}\frac{r(h_{1},h_{2})}{|(h_{1},h_{2})|}=0$$

$\textcolor{Red}{\textbf{Diferenciabilidad implica continuidad de Funciones de $\mathbb{R}^{2}\rightarrow \mathbb{R}$}}$

$\textbf{Teorema 1.}$ Si la función $f:A\subset\mathbb{R}^{2}\rightarrow \mathbb{R}$ definida en $A$ de $\mathbb{R}^{2}$, es diferenciable en el ´punto $p=(x_{0},y_{0})\in A$, entonces es continua en ese punto.

$\small{Demostración.}$ Si f es diferenciable en el ´punto $p=(x_{0},y_{0})\in A$ se tiene
$$f((x_{0},y_{0})+(h_{1},h_{2}))=f(x_{0},y_{0})+\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}+r(h_{1},h_{2})$$
tomando limite se tiene
$$\lim_{(h_{1},h_{2})\rightarrow(0,0)}f((x_{0},y_{0})+(h_{1},h_{2}))=\lim_{(h_{1},h_{2})\rightarrow(0,0)}f(x_{0},y_{0})+\cancel{\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}}+\cancel{\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}}+\cancel{r(h_{1},h_{2})}$$
se tiene entonces que
$$\lim_{(h_{1},h_{2})\rightarrow(0,0)}f((x_{0},y_{0})+(h_{1},h_{2}))=f(x_{0},y_{0})$$
por lo que f es continua en $(x_{0},y_{0})$

$\textcolor{Red}{\textbf{Aplicacion del Teorema del Valor Medio de Funciones de $\mathbb{R}^{2}\rightarrow \mathbb{R}$}}$

$\textbf{Teorema 2.}$ Suponga que $f:A\subset\mathbb{R}^{2}\rightarrow\mathbb{R}$ es tal que
$$\left|\frac{\partial f}{\partial x}(x_{0},y_{0})\right|\leq M$$ y $$\left|\frac{\partial f}{\partial x}(x_{0},y_{0})\right|\leq M$$

donde $M$ no depende de $x,y$ entonces $f$ es continua en $A$.

$\small{Demostración.}$ Sean $(x_{0},y_{0}),(x_{0}+h_{1},y_{0}+h_{2})\in A$ tenemos entonces que $$f(x_{0}+h_{1},y_{0}+h_{2})-f(x_{0},y_{0})=f(x_{0}+h_{1},y_{0}+h_{2})\textcolor{Red}{-f(x_{0}+h_{1},y_{0})+f(x_{0}+h_{1},y_{0})}-f(x_{0},y_{0})$$ Aplicando teorema del valor medio se tiene que existen $\xi_{1},\in\ (x_{0},x_{0}+h_{1})$,$\xi_{2}\in(y_{0},y_{0}+h_{2})$ tal que $$f(x_{0}+h_{1},y_{0}+h_{2})\textcolor{Red}{-f(x_{0}+h_{1},y_{0})}=\frac{\partial f}{\partial y}(x_{0}+h_{1},\xi_{2})h_{2}$$ $$\textcolor{Red}{f(x_{0}+h_{1},y_{0})}-f(x_{0},y_{0})=\frac{\partial f}{\partial x}(\xi_{1},y_{0}+h_{2})h_{1}$$ por lo tanto $$\left|f(x_{0}+h_{1},y_{0}+h_{2})-f(x_{0},y_{0})\right|=\left|\left(\frac{\partial f}{\partial y}(x_{0}+h_{1},\xi_{2})h_{2}\right)+\left(\frac{\partial f}{\partial x}(\xi_{1},y_{0}+h_{2})h_{1}\right)\right|\leq $$ $$\left|\left(\frac{\partial f}{\partial y}(x_{0}+h_{1},\xi_{2})\right)\right||h_{2}|+\left|\left(\frac{\partial f}{\partial x}(\xi_{1},y_{0}+h_{2}\right)\right|)|h_{1}|\leq M(|h_{2}|+|h_{1}|)$$ si tenemos que $\displaystyle{|(h_{1},h_{2})|}<\delta$ entonces $$M(|h_{2}|+|h_{1}|)<2M\delta~\therefore~~~\epsilon=2M\delta\Rightarrow \delta=\frac{\epsilon}{2M}$$

$\textcolor{Red}{\textbf{Diferenciabilidad y Derivadas Direccionales}}$

$\textbf{Teorema 3.}$ Si $f:\mathbb{R}^{n}\rightarrow \mathbb{R}$ es una función diferenciable en $x_{0}$ en la dirección del vector unitario u entonces
$$\frac{\partial f}{\partial u}(x_{0})=\sum_{i=1}^{n}\frac{\partial~f}{\partial x_{i}}\cdot u_{i}$$

$\small{Demostración.}$

Sea $u\in\mathbb{R}^{n}$ tal que $u\neq0$ y $|u|=1$ como $f$ es diferenciable en
$x_{0}$, se tiene que
$$f(x_{0}+h)-f(x_{0})=\sum_{i=1}^{n}\frac{\partial f}{\partial x_{i}}(x_{0})h_{i}+r(h)$$satisface
$$\lim_{(h)\rightarrow 0}\frac{r(h)}{|(h)|}=0$$
tomando $h=tu$ se tiene $|h|=|tu|=|t||u|=|t|$\
se tiene entonces
$$f(x_{0}+t(u))-f(x_{0})=\sum_{i=1}^{n}\frac{\partial f}{\partial x_{i}}(x_{0})tu_{i}+r(tu)$$
tenemos entonces
$$\lim_{t\rightarrow0}\frac{f(x_{0}+t(u))-f(x_{0})}{t}=\sum_{i=1}^{n}\frac{\partial f}{\partial x_{i}}(x_{0})u_{i}+\cancel{\lim_{t\rightarrow0}r(tu)}$$
es decir
$$\frac{\partial f}{\partial u}(x_{0})=\sum_{i=1}^{n}\frac{\partial f}{\partial x_{i}}(x_{0})u_{i}$$ $\square$

$\textbf{Ejemplo.}$ Halle la derivada direccional de $f(x,y)=\ln(x^{2}+y^{3})$ en el punto $(1,-3)$ en la dirección $(2,-3)$

$\small{Solución.}$

En este caso
$$u=(2,-3)~\Rightarrow~|u|=\sqrt{13}~\rightarrow~\frac{u}{|u|}=\left(\frac{2}{\sqrt{13}},\frac{-3}{\sqrt{13}}\right)$$

$$\frac{\partial f}{\partial x}(1,-3)=\frac{2x}{x^{2}+y^{3}}\left|_{(1,-3)}\right.=\frac{-2}{26}$$

$$\frac{\partial f}{\partial y}(1,-3)=\frac{3y^{2}}{x^{2}+y^{3}}\left|_{(1,-3)}\right.=\frac{-27}{26}$$

por lo tanto
$$D_{\left(\frac{2}{\sqrt{13}},\frac{-3}{\sqrt{13}}\right)}f\left(1,-3\right)=\left(\frac{-2}{26}\right)\cdot\left(\frac{2}{\sqrt{13}}\right)+\left(\frac{-27}{26}\right)\cdot \left(\frac{-3}{\sqrt{13}}\right)=\frac{77\sqrt{13}}{338}$$

$\textcolor{Red}{\textbf{El Gradiente}}$

Sea $f:A\subset \mathbb{R}^{n}\rightarrow \mathbb{R}$ una función diferenciable en $x_{0}\in A$. Entonces el vector cuyas componentes
son las derivadas parciales de f en $x_{0}$ se le denomina Vector Gradiente
$$\left(\frac{\partial f}{\partial x_{1}}(x_{0}),\frac{\partial f}{\partial x_{2}}(x_{0}),…,\frac{\partial f}{\partial x_{n}}(x_{0}),\right)$$
y se le denota por $\nabla f$.

En el caso particular $n=2$ se tiene
$$\nabla f(x_{0})=\left(\frac{\partial f}{\partial x}(x_{0}),\frac{\partial f}{\partial y}(x_{0})\right)$$
En el caso particular $n=3$ se tiene
$$\nabla f(x_{0})=\left(\frac{\partial f}{\partial x}(x_{0}),\frac{\partial f}{\partial y}(x_{0}),\frac{\partial f}{\partial z}(x_{0})\right)$$

$\textbf{Ejemplo.}$ Calcular $\nabla f$ para $f(x,y)=x^{2}y+y^{3}$
$\small{Solución}$En este caso
$$\nabla f(x,y)=\left(2xy,x^{2}+3y^{2}\right)$$

$\textbf{Teorema 4.}$ Si $f:\mathbb{R}^{2}\rightarrow \mathbb{R}$ es una función diferenciable en $(x_{0},y_{0})$ en la dirección del vector unitario u entonces
$$\frac{\partial f}{\partial u}(x_{0},y_{0})=\nabla f(x_{0},y_{0})\cdot u$$

Sea $u\in\mathbb{R}^{n}$ tal que $u\neq0$ y $|u|=1$ como $f$ es diferenciable en
$(x_{0},y_{0})$, se tiene que
$$f((x_{0},y_{0})+(h_{1},h_{2}))=f(x_{0},y_{0})+\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}+r(h_{1},h_{2})$$

satisface
$$\lim_{(h_{1},h_{2})\rightarrow(0,0)}\frac{r(h_{1},h_{2})}{|(h_{1},h_{2})|}=0$$
tomando $h=tu$ se tiene $|h|=|(h_{1},h_{2})|=|tu|=|t||u|=|t|$

se tiene entonces
$$f((x_{0},y_{0})+t(u))=f(x_{0},y_{0})+\frac{\partial f}{\partial x}(x_{0},y_{0})tu_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})tu_{2}+r(tu_{1},ru_{2})$$
y también
$$\frac{r(h_{1},h_{2})}{|(h_{1},h_{2})|}=\frac{r(tu_{1},ru_{2})}{|tu|}=\frac{r(tu_{1},ru_{2})}{|t||u|}=\frac{r(tu_{1},ru_{2})}{|t|}$$
tenemos entonces
$$\lim_{t\rightarrow0}\frac{r(tu_{1},ru_{2})}{|t|}=\lim_{t\rightarrow0}\frac{f((x_{0},y_{0})+t(u))-f(x_{0},y_{0})}{|t|}-\frac{\frac{\partial f}{\partial x}(x_{0},y_{0})tu_{1}}{|t|}-\frac{\frac{\partial f}{\partial y}(x_{0},y_{0})tu_{2}}{|t|}$$
es decir
$$0=\frac{\partial f}{\partial u}(x_{0},y_{0})-\frac{\partial f}{\partial x}(x_{0},y_{0})u_{1}-\frac{\partial f}{\partial y}(x_{0},y_{0})u_{2}$$
y en consecuencia

$$\frac{\partial f}{\partial u}(x_{0},y_{0})=\frac{\partial f}{\partial x}(x_{0},y_{0})u_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})u_{2}=\left(\frac{\partial f}{\partial x}(x_{0},y_{0},\frac{\partial f}{\partial y}(x_{0},y_{0}\right)\cdot\left(u_{1},u_{2}\right)=\nabla f(x_{0},y_{0})\cdot u$$ $\square$

$\textbf{Ejemplo.}$ Halle la derivada direccional de $f(x,y)=\ln(x^{2}+y^{3})$ en el punto $(1,-3)$ en la dirección $(2,-3)$

$\small{Solución.}$ En este caso

$$\frac{\partial f}{\partial x}(1,-3)=\frac{2x}{x^{2}+y^{3}}\left|_{(1,-3)}\right.=\frac{-2}{26}$$

$$\frac{\partial f}{\partial y}(1,-3)=\frac{3y^{2}}{x^{2}+y^{3}}\left|_{(1,-3)}\right.=\frac{-27}{26}$$

por lo tanto
$$\nabla f(1,-3)=\left(\frac{-2}{26},\frac{-27}{26}\right)\cdot \left(\frac{2}{\sqrt{13}},\frac{-3}{\sqrt{13}}\right)=\frac{77}{26\sqrt{13}}=\frac{77\sqrt{13}}{338}$$

$\textcolor{Red}{\textbf{Dirección de Mayor Crecimiento de una Función}}$

$\textbf{Teorema 5.}$ Supongamos que $\nabla(f(x))\neq(0,0,0)$. Entonces $\nabla(f(x))$ apunta en la dirección a lo largo de la cual f crece más rápido.

$\small{Demostración.}$ Si v es un vector unitario, la razón de
cambio de f en la dirección v está dada por $\nabla(f(x))\cdot v$ y
$\nabla(f(x)) \cdot v$ = $|\nabla{f(x)}|~|v|\cos\Theta$ = $|\nabla{f(x)}|\cos\Theta$,
donde $\Theta$ es el ángulo entre $\nabla{f}$, $v$. Este es máximo cuando $\Theta~=~0$ y esto ocurre cuando $v$, $~\nabla{f}$ son paralelos. En otras palabras, si queremos movernos en una dirección en la cual $f$ va a crecer más rápidamente, debemos proceder en la dirección $\nabla{f(x)}$. En forma análoga, si queremos movernos en la dirección en la cual $f$ decrece más rápido, habremos de proceder
en la dirección $-\nabla{f}$.

$\textbf{Ejemplo.}$ Encontrar la dirección de rapido crecimiento en $(1,1,1)$ para $\displaystyle{f(x,y,z)=\frac{1}{\sqrt{x^{2}+y^{2}+z^{2}}}}$

$\small{Solución.}$ En este caso

$$\nabla f(1,1,1)=\left(\frac{\partial \left(\frac{1}{\sqrt{x^{2}+y^{2}+z^{2}}}\right)}{\partial x},\frac{\partial \left(\frac{1}{\sqrt{x^{2}+y^{2}+z^{2}}}\right)}{\partial y},\frac{\partial \left(\frac{1}{\sqrt{x^{2}+y^{2}+z^{2}}}\right)}{\partial z}\right)\left|_{(1,1,1)}\right.=$$

$$\left(-\frac{x}{\sqrt{x^{2}+y^{2}+z^{2}}},-\frac{y}{\sqrt{x^{2}+y^{2}+z^{2}}},-\frac{z}{\sqrt{x^{2}+y^{2}+z^{2}}}\right)\left|_{(1,1,1)}\right.=-\frac{1}{3\sqrt{3}}\left(1,1,1\right)$$
Podemos tomar

$$u=\frac{\nabla f}{|\nabla f|}$$
en este caso
$$u=\frac{-\frac{1}{3\sqrt{3}}\left(1,1,1\right)}{\frac{1}{3}}=\left(-\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}},-\frac{1}{\sqrt{3}}\right)$$

$\textcolor{Red}{\textbf{Puntos Estacionarios}}$

$\textbf{Definición.}$ Sea $f:\Omega\subset \mathbb{R}^{n} \rightarrow \mathbb{R}$ diferenciable, a los puntos $x\in \Omega$ tales que $\nabla f(x)=0$ se les llama puntos críticos (o punto estacionario) de la función.

$\textbf{Ejemplo.}$ Sea $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=x^{2}-y^{2}$ hallar los puntos críticos de $f$

$\small{Solución.}$ Se tiene que $\nabla f(x)=(2x, 2y)$ \hspace{0.5cm}$\nabla f(x)=0\Leftrightarrow(2x, 2y)=(0,0)\Leftrightarrow 2x=0$ y $2y=0\Leftrightarrow x=0$ y $y=0$ \hspace{0.5cm} $\therefore$ $(0,0)$ es el único punto crítico de $f$.

$\textbf{Ejemplo.}$ Que condición se debe satisfacer para que la función $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=ax^{2}+2bxy+cy^{2}+dx-ey+f$ tenga un punto crítico

$\nabla f=(2ax+2by+d, 2bx+2cy-e)$ entonces

$\nabla f=0\Leftrightarrow 2ax+2by+d=0$ y $2bx+2cy-e=0$

$\Rightarrow$ $ 2ax+2by=-d$ y $2bx+2cy=e$ se necesita que

$\Rightarrow$ $2a(2c)-(2b)^{2}\neq 0$ $\therefore$ $ac-b^{2}\neq 0$

$\textcolor{Red}{\textbf{Diferenciación de funciones $\mathbb{R}^{n}\rightarrow\mathbb{R}$}}$

Sea $f:A \subseteq\mathbb{R}^{n}\rightarrow \mathbb{R}$ y $\overline{a}=(a_{1},\ldots,a_{n}) \epsilon {A}$. Se define la derivada pacial $i$-esima en $\overline{a}$ denotada $f_{x}(\overline{a})$, $D_{x}f(\bar{a})$ ó $\displaystyle\frac{\partial f}{\partial x}(\bar{a})$ de la forma $f_{x}=\displaystyle\lim_{h \rightarrow 0}\frac{f(a_{1},\ldots,a_{i}+h,\ldots.a_{n})-f(\bar{a})}{h}=\displaystyle\lim_{h \rightarrow 0}\frac{f(a+he_{i})-f(a)}{h}$ siendo
$\bar{e}_{i}=(0,\ldots,\underset{i-esimo}{1},\ldots,0)$. Si $n=2$ existen 2 derivadas parciales.

Sea $\bar{a}=(x_{0},y_{0})$ un punto del interior del dominio de $f:A \subseteq\mathbb{R}^{2}\rightarrow \mathbb{R}$ las derivas parciales de $f$ en el punto $\bar{a}$ denotada respectivamente por $f_{x}(x_{0},y_{0})$, $f_{y}(x_{0},y_{0})$
son:

$$f_{x}(x_{0},y_{0})=\displaystyle\lim_{h \rightarrow 0}\frac{f(x_{0}+h,y_{0})-f(x_{0},y_{0})}{h}$$

$$f_{y}(x_{0},y_{0})=\displaystyle\lim_{k \rightarrow 0}\frac{f(x_{0},y_{0}+k)-f(x_{0},y_{0})}{k}$$

Sea $f:I\subset\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=x^{2}y^{3}$

Calcular $f_{x},~f_{y}$

En este caso

$$f_{x}=\lim_{h\rightarrow 0}\frac{f(x+h,y)-f(x,y)}{h}$$
$$=\lim_{h\rightarrow 0}\frac{(x+h)^{2}y^{3}-x^{2}y^{3}}{h}$$
$$=\lim_{h\rightarrow 0}2xy^{3}+hy^{3}=2xy^{3}$$
$$f_{y}=\lim_{h\rightarrow 0}\frac{f(x,y+h)-f(x,y)}{h}$$
$$=\lim_{h\rightarrow 0}\frac{x^{2}(y+h)^{3}-x^{2}y^{3}}{h}$$
$$=\lim_{h\rightarrow 0}3x^{2}y^{2}+hy^{3}$$
$$=3x^{2}y^{2}$$

$\textbf{Ejemplo}$ Sea

Calculemos $f_{x}(0,0)$
$$f_{x}(0,0)=\lim_{h\rightarrow 0}\frac{f(0+h,0)-f(0,0)}{h}$$
$$=\lim_{h\rightarrow 0}\frac{\frac{h(0)}{h^{2}}}{h}$$
$$=\lim_{h\rightarrow 0}\frac{0}{h^{3}}=0$$
$$f_{y}(0,0)=\lim_{h\rightarrow 0}\frac{f(0,0+h)-f(0,0)}{h}$$
$$=\lim_{h\rightarrow 0}\frac{\frac{(0)h}{h^{2}}}{h}$$
$$=\lim_{h\rightarrow 0}\frac{0}{h^{3}}=0$$
En este caso $f_{x}=0=f_{y}$ sin embargo la función no es continua

$\textcolor{Red}{\textbf{Derivada Direccional en un punto}}$

Sea $f:A\subseteq\mathbb{R}^{n}\rightarrow \mathbb{R}$ $x_{0}\in A$. Sea $u\in \mathbb{R}^{n}$ con $|u|=1$ la derivada direcional de $f$ en
la dirección del vector $u$, en el punto $x_{0}$ denotada por $\displaystyle{\frac{\partial f}{\partial u}}(x_{0})$, se define por
$$\displaystyle{\frac{\partial f}{\partial u}}(x_{0})=\displaystyle\lim_{h \rightarrow
0}\frac{f(x_{0}+hu)-f(x_{0})}{h}$$

$\textbf{Ejemplo}$ Sea $f(x,y)=x^{2}y$ y sea $\displaystyle{u=\left(\frac{1}{\sqrt{5}},\frac{2}{\sqrt{5}}\right)}$ por lo tanto la derivada direccional en $(x_{0},y_{0})$ es:
$$\lim_{h \rightarrow0}\frac{f\left((x_{0},y_{0})+h\left(\frac{1}{\sqrt{5}},\frac{2}{\sqrt{5}}\right)\right)-f(x_{0},y_{0})}{h}=\lim_{h \rightarrow0}\frac{\left(x_{0}+\frac{h}{\sqrt{5}}\right)^{2}\left(y_{0}+\frac{2h}{\sqrt{5}}\right)-x_{0}^{2}y_{0}}{h}=$$
$$\lim_{h \rightarrow0}\frac{\left(x_{0}^{2}+\frac{2x_{0}h}{\sqrt{5}}+\frac{h^{2}}{5}\right)\left(y_{0}+\frac{2h}{\sqrt{5}}\right)-x_{0}^{2}y_{0}}{h}=\frac{2x_{0}^{2}}{\sqrt{5}}+\frac{2x_{0}y_{0}}{\sqrt{5}}$$

$\small{Notas:}$ 1) La derivada direccional indica la variación de la función en la dirección de $\bar{u}$.
2)Las derivadas parciales son derivadas direccionales respecto a los vectores de la base canonica.

$\textcolor{Red}{\textbf{Diferenciabilidad}}$

$\textbf{Idea Geometrica}$

$y=f'(x_{0})(x-x_{0})+f(x_{0})$
si $x=x_{0}$
$y=f(x_{0})$
si $x=x_{0}+h$
$y=f'(x_{0})h$
$\therefore$ \qquad $r(h)=f(x_{0}+h)-f(x_{0})-f'(x_{0})h \qquad$ (Diferencial)
donde
$$\frac{r(h)}{h}=\frac{f(x_{0}+h)-f(x_{0})}{h}-f'(x_{0})$$
Debería ocurrir
$$\lim_{h\rightarrow 0}\frac{r(h)}{h}=0$$

$\textbf{Definición}$ Sea $A\subset\mathbb{R}^{2}$, un abierto, $f:A\rightarrow\mathbb{R}$ y $(x_{0},y_{0})\in A$. Se dice que f es diferenciable en $(x_{0},y_{0})$ si existen constantes $A_{1},~~A_{2}$ tal que
$$f((x_{0},y_{0})+(h_{1},h_{2}))=f(x_{0},y_{0})+A_{1}h_{1}+A_{2}h_{2}+r(h_{1},h_{2})$$donde
$$\lim_{(h_{1},h_{2})\rightarrow(0,0)}\frac{r(h_{1},h_{2})}{|(h_{1},h_{2})|}=0$$

En la definición anterior si se toma $h=(h_{1},0)$ se tiene
$$f((x_{0},y_{0})+(h_{1},0))=f(x_{0},y_{0})+A_{1}h_{1}+A_{2}(0)+r(h_{1},0)$$donde
$$\lim_{h_{1}\rightarrow0}\frac{f(x_{0}+h_{1},y_{0})-f(x_{0},y_{0})}{h_{1}}-A_{1}=\lim_{h_{1}\rightarrow0}\frac{r(h_{1},0)}{h_{1}}$$
como

$$\lim_{h_{1}\rightarrow0}\frac{r(h_{1},0)}{h_{1}}=0$$se tiene
$$\lim_{h_{1}\rightarrow0}\frac{f(x_{0}+h_{1},y_{0})-f(x_{0},y_{0})}{h_{1}}-A_{1}=0$$
en consecuencia

$$\frac{\partial f}{\partial x}=\lim_{h_{1}\rightarrow0}\frac{f(x_{0}+h_{1},y_{0})-f(x_{0},y_{0})}{h_{1}}=A_{1}$$
En la definición anterior si se toma $h=(0,h_{2})$ se tiene
$$f((x_{0},y_{0})+(0,h_{2}))=f(x_{0},y_{0})+A_{1}(0)+A_{2}h_{2}+r(0,h_{2})$$donde
$$\lim_{h_{2}\rightarrow0}\frac{f(x_{0},y_{0}+h_{2})-f(x_{0},y_{0})}{h_{2}}-A_{2}=\lim_{h_{2}\rightarrow0}\frac{r(0,h_{2})}{h_{2}}$$
como
$$\lim_{h_{2}\rightarrow0}\frac{r(0,h_{2})}{h_{2}}=0$$se tiene
$$\lim_{h_{0}\rightarrow0}\frac{f(x_{0},y_{0}+h_{2})-f(x_{0},y_{0})}{h_{2}}-A_{2}=0$$
en consecuencia

$$\frac{\partial f}{\partial y}=\lim_{h_{2}\rightarrow0}\frac{f(x_{0},y_{0}+h_{2})-f(x_{0},y_{0})}{h_{2}}=A_{2}$$

$\textbf{Definición}$ Sea $A\subset\mathbb{R}^{2}$, un abierto, $f:A\rightarrow\mathbb{R}$ y $(x_{0},y_{0})\in A$. Se dice que f es diferenciable en $(x_{0},y_{0})$ si existen las derivadas parciales $\displaystyle{\frac{\partial f}{\partial x}(x_{0},y_{0}),~~\frac{\partial f}{\partial y}}(x_{0},y_{0})$ tal que
$$f((x_{0},y_{0})+(h_{1},h_{2}))=f(x_{0},y_{0})+\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}+r(h_{1},h_{2})$$donde
$$\lim_{(h_{1},h_{2})\rightarrow(0,0)}\frac{r(h_{1},h_{2})}{|(h_{1},h_{2})|}=0$$

$\textbf{Proposición 1}$ Sea $f:\mathbb{R}^{2}\rightarrow
\mathbb{R}$ tal que $$\lim_{(x,y)\rightarrow (a,b)}f(x,y)=L$$
Entonces para una función real y continua $g$ definida en un
entorno da $a$ tal que $$\lim_{x\rightarrow a}g(x)=b$$ se tiene que $$\lim_{x\rightarrow a}f(x,g(x))=L$$

$Demostración.$ Por la existencia del límite doble, dado $\epsilon>0$ existe un $\delta>0$, tal que $$|(x,y)-(a,b)|<\delta \Rightarrow |f(x,y)-L|<\epsilon.$$ Ahora $$\lim_{x\rightarrow a}g(x)=b$$ quiere decir que dado $\delta>0$ existe $\sigma>0$, con $0<\sigma<\delta$ tal que: $$|x-a|<\sigma \Rightarrow |g(x)-b|<\delta.$$ Por
tanto, si $|x-a|<\sigma$, se tiene que $|(x,g(x))-(a,b)|<\delta.$ Con lo cual, $$|f(x,g(x))-L|<\epsilon$$ $\square$

$\small{Ejemplo:}$ Determinar si existe, el límite de la función definida por

$$f(x,y)=\left{\begin{matrix} \frac{x^{2}y}{x^{2}+y^{2}}&(x,y)\neq (0,0)\ 0&(x,y)=(0,0) \end{matrix}\right.$

Para determinar su límite podemos acercarnos por trayectorias (funciones continuas) al origen.

Pongamos $y=g(x)=0$ se tiene entonces que

$$\lim_{(x,y)\rightarrow(0,0)}f(x,y)=\lim_{(x,y)\rightarrow(0,0)}f(x,g(x))=\lim_{(x,y)\rightarrow(0,0)}f(x,0)=\lim_{x\rightarrow0}\frac{x^{2}0}{x^{2}+0^{2}}=0$$
Pongamos ahora $y=g(x)=x$ se tiene entonces que
$$\lim_{(x,y)\rightarrow(0,0)}f(x,y)=\lim_{(x,y)\rightarrow(0,0)}f(x,g(x))=\lim_{(x,x)\rightarrow(0,0)}f(x,x)=\lim_{x\rightarrow0}\frac{x^{2}x}{x^{2}+x^{2}}=\lim_{x\rightarrow0}\frac{x^{3}}{2x^{2}}=0$$
Lo anterior nos dice que si existe el límite, éste tendría que ser 0, para comprobarlo usaremos la definición, se tiene entonces que debemos hallar un $\delta>0$ tal que
$\left|\frac{x^{2}y}{x^{2}+y^{2}}\right|<\epsilon$ siempre que $|(x,y)-(0,0)|<\delta$. Observamos que
$$\left|\frac{x^{2}y}{x^{2}+y^{2}}\right|=\frac{|x^{2}||y|}{|x^{2}+y^{2}|}=\frac{|x|^{2}|y|}{|x^{2}+y^{2}|}\leq
\frac{|\overline{x}|^{2}|\overline{x}|}{|\overline{x}|^{2}}=|\overline{x}|<\delta.$$
$\therefore$ podemos tomar $\delta=\epsilon$

$\small{Ejemplo:}$ Determinar si existe, el límite de la función definida por

$$f(x,y)=\left\{\begin{matrix}
\frac{xy}{x^{2}+y^{2}}&(x,y)\neq (0,0)\
\overline{0}&(x,y)=(0,0)
\end{matrix}.$$

Para determinar su límite podemos acercarnos por trayectorias (funciones continuas) al origen.

Pongamos $y=g(x)=x$ se tiene entonces que

$$\lim_{(x,y)\rightarrow(0,0)}f(x,y)=\lim_{(x,y)\rightarrow(0,0)}f(x,g(x))=\lim_{(x,x)\rightarrow(0,0)}f(x,x)=\lim_{x\rightarrow0}\frac{x^{2}}{x^{2}+x^{2}}=\frac{1}{2}$$

Pongamos $y=g(x)=0$ se tiene entonces que

$$\lim_{(x,y)\rightarrow(0,0)}f(x,y)=\lim_{(x,y)\rightarrow(0,0)}f(x,g(x))=\lim_{(x,0)\rightarrow(0,0)}f(x,0)=\lim_{x\rightarrow0}\frac{x (0)}{x^{2}+0^{2}}=0$$

como $\frac{1}{2}\neq 0$ entonces $\cancel{\exists}$ el límite de la función.

$\textcolor{Red}{\textbf{Continuidad de Funciones de $\mathbb{R}^{n} \rightarrow \mathbb{R}$}}$

$Definición 1.$ Sea $f:\Omega\subset\mathbb{R}^{n} \rightarrow
\mathbb{R}$, y sea $x_{0}$ un punto de acumulación de $\Omega$.Se dice que $f(x_{0})\in\mathbb{R}$ es el límite de $f$ en $x_{0}$, y se denota por: $$\displaystyle\lim_{x\rightarrow x_{0}}f(x)=f(x_{0})$$ Si dado $\varepsilon > 0$, existe $\delta > 0$ tal que $|f(x)-f(x_{0})|<\varepsilon$ cuando $x \in \Omega$,
$0<|x-x_{0}|<\delta$

$\small{Ejemplo:}$ Demostrar la continuidad en $\mathbb{R}^2$ de la función $f(x,y)=xy$.

p.d. Dado $\epsilon>0$ $\exists$ $\delta>0$ tal que $|xy-ab|\leq \epsilon$ siempre que $0<|x-a|<\delta_1$ y $0<|y-b|\leq \delta_2$ tenemos que:

$|xy-ab|
=|xy-xb+xb-ab|
\leq |x(y-b)|+|b(x-a)|
\leq \left(|x-a|+|a|\right)|y-b|+|b||x-a|\leq \left(\delta+|a|\right)\delta+|b|\delta
=\delta\underset{\underset {\text{Esta la podemos acotar}}{\searrow\ \ \ \ \ \ \ \ \ \ \ \
}}{\left(\left(\delta+|a|\right)+|b|\right)}$

Si $\delta=1$ tenemos que $\delta(1+|a|+|b|)$ y asi tomamos

$$\delta=mín \left\{ 1 , \frac{\epsilon}{1+|a|+|b|}\right\}$$

$\textcolor{Red}{\textbf{Diferenciación de funciones $\mathbb{R}^{n}\rightarrow\mathbb{R}$}}$

Sea $f:A \subseteq\mathbb{R}^{n}\rightarrow \mathbb{R}$ y $\overline{a}=(a_{1},\ldots,a_{n})\epsilon$ $A$. Se define la derivada pacial $i$-esima en $\overline{a}$ denotada $f_{x}(\overline{a})$, $D_{x}f(\bar{a})$ ó $\displaystyle\frac{\partial f}{\partial x}(\bar{a})$ de la forma $$f_{x}=\displaystyle\lim_{h \rightarrow 0}\frac{f(a_{1},\ldots,a_{i}+h,\ldots.a_{n})-f(\bar{a})}{h}=\displaystyle\lim_{h \rightarrow 0}\frac{f(a+he_{i})-f(a)}{h}$$ siendo $\bar{e}_{i}=(0,\ldots,\underset{i-esimo}{1},\ldots,0)$.

Si $n=2$ existen 2 derivadas parciales.

Sea $\bar{a}=(x_{0},y_{0})$ un punto del interior del
dominio de $f:A \subseteq\mathbb{R}^{2}\rightarrow \mathbb{R}$
las derivas parciales de $f$ en el punto $\bar{a}$ denotada
respectivamente por $f_{x}(x_{0},y_{0})$, $f_{y}(x_{0},y_{0})$
son:

$$f_{x}(x_{0},y_{0})=\displaystyle\lim_{h \rightarrow 0}\frac{f(x_{0}+h,y_{0})-f(x_{0},y_{0})}{h}$$
$$f_{y}(x_{0},y_{0})=\displaystyle\lim_{k \rightarrow 0}\frac{f(x_{0},y_{0}+k)-f(x_{0},y_{0})}{k}$$

$\small{Ejemplo:}$ Si $f(x,y)=x^{2}+x+1$ entonces
$f_{x}(0,0)=1$ ya que $f_{x}=\displaystyle\lim_{h \rightarrow 0}\frac{f(0+h,0)-f(0,0)}{h}=
\displaystyle\lim_{h \rightarrow 0}\frac{h^{2}+h+1-1}{h}=\displaystyle\lim_{h \rightarrow 0}\frac{h(h+1)}{h}=
\displaystyle\lim_{h \rightarrow 0}h+1 = 1$ y $f_{y}=\displaystyle\lim_{k \rightarrow 0}\frac{f(0,0+k)-f(0,0)}{k}=
\displaystyle\lim_{k \rightarrow 0}\frac{1-1}{k}=0$

$\small{Ejemplo:}$ Si $f(x,y)=x^{2}+x+1$ entonces $f_{x}(0,0)=1$ ya que

$f_{x}=\displaystyle\lim_{h \rightarrow 0}\frac{f(0+h,0)-f(0,0)}{h}=
\displaystyle\lim_{h \rightarrow 0}\frac{h^{2}+h+1-1}{h}=\displaystyle\lim_{h \rightarrow 0}\frac{h(h+1)}{h}= \displaystyle\lim_{h \rightarrow 0}h+1 = 1$ y $f_{y}=\displaystyle\lim_{k \rightarrow 0}\frac{f(0,0+k)-f(0,0)}{k}= \displaystyle\lim_{k \rightarrow 0}\frac{1-1}{k}=0$

$\small{Observación:}$ La derivada parcial en un punto de una función de varias variables en la derivada de la función de una variable, obtenida haciendo constante todas las variables, menos una. en consecuencia se pueden aplicar con esta interpretación, las reglas de derivación en una variable.

Las derivadas parciales en el punto $(x_{0},y_{0})$ de la función $z=f(x,y)$ representa la pendiente de las curvas intersección $C_{1}$ y $C_{2}$ de la superficie $z=f(x,y)$ con los planos $y=y_{0}$, $x=x_{0}$ respectivamente

$\small{Ejercicio:}$ Calcular las derivadas parciales

$a)$ $f(x,y)=a\arcsin(x-y)$

$b)$ $f(t,u)=\displaystyle\frac{\cos(2tu)}{t^{2}+u^{2}}$

$c)$ $f(x,y,z)=\displaystyle\frac{xyz}{x^{2}+y^{2}+z^{2}}$

$d)$ $f(x,y)=\displaystyle\int_{0}^{\sqrt{xy}}e^{-t^{2}}dt \qquad x>0, \, y>0$

$\small{Solución:}$

$a)$ $f_{x}=\displaystyle\frac{x}{\sqrt{1-(x-y)^{2}}}+ \arcsin(x-y)$

$f_{y}=\displaystyle\frac{-x}{\sqrt{1-(x-y)^{2}}}$

$b)$ $f_{t}=\displaystyle\frac{-(t^{2}+u^{2})\sin(2tu)\cdot2u-\cos(2tu)2t}{(t^{2}+u^{2})^{2}}$

$f_{u}=\displaystyle\frac{(t^{2}+u^{2})-\sin(2tu)2u-\cos(2tu)2u}{(t^{2}+u^{2})^{2}}$

$c)$ $f_{x}=\displaystyle\frac{(x^{2}+y^{2}+z^{2})yz-xyz(2x)}{(x^{2}+y^{2}+z^{2})^{2}}$

$f_{y}=\displaystyle\frac{(x^{2}+y^{2}+z^{2})xz-xyz(2y)}{(x^{2}+y^{2}+z^{2})^{2}}$

$f_{z}=\displaystyle\frac{(x^{2}+y^{2}+z^{2})xy-xyz(2z)}{(x^{2}+y^{2}+z^{2})^{2}}$

$d)$ $f_{x}=\displaystyle e^{-xy}\frac{y}{2\sqrt{xy}}$

$f_{y}=\displaystyle e^{-xy}\frac{x}{2\sqrt{xy}}$

$\textcolor{Red}{\textbf{Criterio de Convergencia de Cauchy}}$

$\textbf{Definición.-}$ Sea ${\overline{x_{k}}}$ una sucesión de puntos de $\mathbb{R}^{n}$. Se dice que ${\overline{x_{k}}}$ es una sucesión de Cauchy si dado $\epsilon>0$ $\exists N_{0}\in \mathbb{N}$ tal que $|\overline{x_{k}}-\overline{x_{l}}|<\epsilon$ $\forall k,l\geq N_{0}$

$\textbf{Teorema 1.-}$ Una sucesión $\overline{x_{k}}\in \mathbb{R}^{n}$ es convergente si y solo si cumple el criterio de Cauchy

$Demostración$ $\textcolor{Red}{\Rightarrow}$ Suponemos que ${\overline{x_{k}}}\rightarrow \overline{x}$ $\therefore$ $|\overline{x_{k}}-\overline{x}|<\epsilon$ $\forall k>N_{0}$. Se tiene entonces que $$|\overline{x_{k}}-\overline{x_{l}}|=|\overline{x_{k}}-\overline{x}+\overline{x}-\overline{x_{l}}|\leq |\overline{x_{k}}-\overline{x}|+|\overline{x}-\overline{x_{l}}|<\frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon$$ $\forall k,l>N_{0}$ $\therefore$ ${\overline{x_{k}}}$

$\textcolor{Red}{\Leftarrow}$ Supongamos que ${\overline{x_{k}}}$ cumple la condición de Cauchy por tanto se tiene que: $$|\overline{x_{k}}-\overline{x_{l}}|<\epsilon\Rightarrow |x_{i,k}-x_{i,l}|<\epsilon\quad \forall i\Rightarrow {x_{i,k}}\quad cumple\quad Cauchy$$ $\therefore$ $x_{i,k}$ es convergente $\forall i$ $\therefore$ ${\overline{x_{k}}}$ es convergente. $\square$

$\textbf{Teorema 2.-}$ (Bolzano-Wierstrass) Toda sucesión $\overline{x_{k}}$ en $\mathbb{R}^{n}$ acotada tiene un punto limite. Dicho de otro modo, toda sucesión en $\mathbb{R}^{n}$ tiene una subsucesión convergente

$Demostración$ Sea $\overline{x_{k}}$ en $\mathbb{R}^{n}$ suponiendo $\overline{x_{k}}$ es acotada, entonces cada $x_{i,k}$ es acotada $\therefore$ según el teorema de Bolzano-Wierstrass para sucesiones en $\mathbb{R}$, ${x_{i,k}}$ tiene una subsucesión convergente $\alpha_{i,k}$ la cual es una sucesión convergente, $\therefore$ podemos formar la sucesiòn $\overline{x_{\alpha,k}}={x_{\alpha,1,k},x_{\alpha,2,k},…,x_{\alpha,n,k}}$ la cual es una sucesión convergente, pero $\overline{x_{\alpha,k}}$ es subsucesión de $\overline{x_{k}}$ $\therefore$ $\overline{x_{k}}$ tiene una subsucesión convergente. $\square$

$\textcolor{Red}{\textbf{Criterio de Convergencia de Cauchy}}$

Una colección $g$ de conjuntos abiertos cuya unión
contiene a $K$ con frecuencia se llama cubierta de $K$.
De modo que el requisito para que $K$ sea compacto
es que toda cubierta $g$ de $K$ se pueda sustituir por
una cubierta finita $g$ de $K$.

$Ejemplo$ Sea $k={x_{1},x_{2},…,x_{m}}$ un subconjunto finito de $\mathbb{R}^{n}$ si $G={G_{\alpha}}$ es una colección de abiertos tal que $k\subset{G_{\alpha}}$ y si todo punto de k pertenece a algún subconjunto de ${G_{\alpha}}$ entonces cuando más m subconjuntos de ${G_{\alpha}}\supset k$ $\therefore$ k es un subconjunto compacto de $\mathbb{R}^{n}$.

$Ejemplo$ Considere al subconjunto $H=\left\{x\in \mathbb{R}| x\geq0\right\}$. Sea $G_{n}=(-1,n)$ $n\in \mathbb{N}$ de tal manera que ${G_{n}| n\in \mathbb{N}}$ sea una colección de subconjuntos abiertos de $\mathbb{R}$ cuya union contenga a $H$. Si ${G_{n_{1}}, G_{n_{2}},…,G_{n_{k}}}$ es una subcolección finita de ${G_{n}|n\in\mathbb{N}}$. Sea $M=sup\left\{n_{1},n_{2},…,n_{k}\right\}$ de tal manera que $G_{n_{j}} \subset G_{n_{k}}$ de aquí deducimos que $G_{M}$ es la unión de
${G_{n_{1}}, G_{n_{2}},…,G_{n_{k}}}$. Sin embargo el número real $M$ no pertenece a $G_{M}$ y por lo tanto no pertenece a $\bigcup_{j=1}^{k}G_{n_{j}}$. En consecuencia, ninguna unión finita de ${G_{n}|n\in\mathbb{N}}$ puede contener a $H$.$\therefore$ $H$ no es compacto.

$Ejemplo$ Demuestrese que todo intervalo cerrado $[a, b]$ de $\mathbb{R}$ es compacto.
$Demostración$ Supongamos un recubrimiento abierto $[a, b]$ tal que no admite subrecubrimiento finito. Entonces tampoco existe un subrecubrimiento finito para

$[a, c]$ $[c; b]$ con $c$ punto medio. Sea $[a_1, b_1] = [a, c]$ el intervalo para el cual no existe el subrecubrimiento finito.

Sea $[a_1, b_1] = [a, c]$ el intervalo para el cual no existe el subrecubrimiento finito.

Sea $p$ el punto de intersección y sea $U$ el recubrimiento que contiene a $p$ y sea $[p-\varepsilon,p+\varepsilon]\subset U$. Entonces existe $r \in \mathbb{N}$ tal que $\forall n > r$,$\frac{b-a}{2^n} < \varepsilon$ y $\forall \, n\geq r$ $[a_n,b_n]\subset U \underset{\circ}{\bigtriangledown}$ ya que ningun $[a_k, b_k]$ admitía un subrecubrimiento finito.

$Ejemplo$ Sea $H=(0,1)$ en $\mathbb{R}$. Si $G_{n}={\frac{1}{n},1-\frac{1}{n}}$ para $n>0$ entonces la colección${G_{n_{1}},G_{n_{2}},…,G_{n_{k}}}$ es una subcolección finita de ${G_{n}| n>2}$. Sea $M=sup{n_{1},…,n_{k}}$ de tal manera que $G_{n_{j}} \subset G_{M}$ se ifiere que $G_{M}$ es la unión de ${G_{n_{1}},G_{n_{2}},…,G_{n_{k}}}$ sin embargo el número real $\frac{1}{m}$ pertenece a $H$ pero no pertenece a $G_{M}$ $\therefore$ ninguna subcolecciónfinita de $\left\{G_{n}~|~ n>2\right\}$ puede formar una subcolección finita para $H$ $\therefore$ $H$ no es compacto.

$\textcolor{Red}{\textbf{Compactos por sucesiones}}$

$\textbf{Teorema 3.-}$ Sea $A\subset \mathbb{R}^{n}$ tal que para todo recubrimiento abierto $\left\{A_{i}\right\}_{i\in I}$ admite un subrecubrimiento finito es decir $\displaystyle{A\subset \bigcup_{i}^{n}A_{i}}$ entonces toda sucesión de puntos de $A$ tiene una subsucesión convergente hacia un punto que pertenece a $A$

$Demostración$ Supongamos que exite una sucesión $\overline{x}{n}\in A$ que no tuviera una subsucesión convergente (en este caso $\overline{x}_{n}$ tiene infinitos elementos). Sea $\overline{x}\in A$ como $\lim_{n\rightarrow\infty}\overline{x}{n}\neq \overline{x}$, existe $\delta{x}>0$ tal que en la bola abierta $B(\overline{x},\delta_{x})$ solo hay a lo más un número finito de elementos de $\overline{x}_{n}$. Entonces la familia de abiertos ${B(\overline{x},\delta{x})}$ es un recubrimiento abierto de A; por hipótesis este recubrimiento admite un subrecubrimiento finito $A_{x_{1}},A_{x_{2}},…,A_{x_{n}}$ de estos abiertos. Por lo tanto los infinitos elementos de $\overline{x}_{n}$ que estan en $A$ pueden ser cubiertos por un número finito de conjuntos abiertos $\underset{\circ}{\bigtriangledown}$ pues cada $A{x_{i}}$ cubre a lo mas un número finito de elementos de $A$.

$\textbf{Teorema 4.-}$ Si toda sucesión de puntos de $A$ tiene una subsucesión convergente hacia un punto que pertenece a $A$ entonces $A$ es cerrado y acotado.

$Demostración$ $\textcolor{red}{\textbf{(A es cerrado)}}$ Sea $\overline{a}\in\mathbb{R}^{n}$ tal que $\overline{a}\in \partial A$ vamos a ver que $\overline{a}\in A$. Como $\overline{a}\in \partial A$ entonces $\forall~r>0$ $B(\overline{a},r)\bigcap A\neq \emptyset$ consideremos ahora $r=\frac{1}{n}$ y en cada bola abierta $\displaystyle{(\overline{a},\frac{1}{n}}$ hay algún punto de $A$ al que podemos llamar $\overline{x}{n}$ de esta manera construimos una sucesión de puntos de $A$ que convergen a $\overline{a}$ por lo tanto por hipótesis $\overline{a}\in A$ por tanto $A$ es cerrado.

$\textcolor{red}{\textbf{(A es cerrado)}}$ Si $A$ no fuera acotado, existiria una sucesión $\overline{x}_{n}$ de puntos de $A$ tal que $\lim_{n\rightarrow\infty}\overline{x}_{n}=\infty$ y este límite no estaría en $A$ $\underset{\circ}{\bigtriangledown}$ por tanto $A$ es acotado.

$Teorema$ $\textcolor{red}{\textbf{(Heine-Borel)}}$ Todo subconjunto cerrado y acotado es compacto.

$1.-$ $K$ compacto implica que $K$ es cerrado.

$Demostración$ Sea $\bar{x} \in K^c$ y sea $G_m =\left\{y \in \mathbb{R}^n | |y-x | > \frac{1}{m}, m \in \mathbb{N}\right\}$ entonces $y \in Ext B(\bar{x}, \frac{1}{m})$ cada $G_m$ es abierta, la unión de todas las $G_m$ consta de todos los puntos de $\mathbb{R}^n$ excepto $x$. Dado que $x \in K$ cada punto de $K$ pertenece a algún $G_m$. Debido a la compacidad de $K$, se infiere que existe $M \in \mathbb{N}$ tal que $K \subset \bigcup_1^m G_i$. Dado que los conjuntos $G_m$ incrementan con $m$, $K \subset G_m$ de donde la vecindad ${z \in \mathbb{R}^n | |z-x| < \frac{1}{m}}$ no intercepta a $K$ demostrando que $K^c$ es abierto $\therefore$ $K$ es cerrado.

$2.-$ $K$ compacto implica que $K$ es acotado.

$Demostración$ Sea $H_m = \left\{ x \in \mathbb{R}^n | \left\| x\right\| < m\right\}$ todo el espacio $\mathbb{R}^n$ y por tanto $K$ está contenido en la unión de los conjuntos crecientes, $H_m$ $m\in \mathbb{N}$. Dado que $K$ es compacto existe $M \in \mathbb{N}$ tal que $K \subset H_m$ por lo que $K$ esta acotado.

Para completar la demostración de este teorema se necesita probar que si $K$ es un subconjunto cerrado y acotado contenido en la unión de una colección $g {G_{\alpha}}$
de conjuntos abiertos en $\mathbb{R}^n$, entonces está contenido en la unión de
algún número finito de conjuntos de $g$.

Dado que $K$ esta acotado, encontramos un punto de acumulación de
$K$, como $K$ es cerrado $y \in K$ y esta en alguna celda abierta, por lo tanto existe $\varepsilon > 0$ tal que para cada $w$ con $|y -w| < \varepsilon $ en la celda abierta y si suponemos que $g ={G_{\alpha}}$ no admite un subrecubrimiento finito llegamos a una contradicción.

$Teorema 6.-$ Si $S$ es un conjunto cerrado y acotado en $\mathbb{R}^{n}$ entonces $S$ es compacto por sucesiones

$Demostración$ Suponga que $S$ es cerrado y acotado, sea ${x_{k}}$ una sucesión de puntos de $S$, se tiene entonces que $S$ es acotada y por el teorema de Bolzano- Weierstrass ${x_{k}}$ tiene una subsucesión convergente ${x_{k_{\alpha}}}$ tal que $x_{k_{\alpha}}\rightarrow x$ y como $S$ es cerrado $x\in S$. $\square$

$\textcolor{Red}{\textbf{Puntos Interiores y Cerradura de un Conjunto}}$

$\textbf{Proposición.}$ Para todo subconjunto $A$ de $\mathbb{R}^n$ se tiene:

$(1)$ $int(A)\subset A$

$\small\textit{Demostración:}$ Si $\bar{a}\in int(A)$ $\exists$ $r>0$ tal que $B(\bar{a},r)\subset A$ $\therefore$ $int(A) \subset A$

$(2)$ $A\subset\bar{A}$

$\small\textit{Demostración:}$ Si $\bar{a}\in A$ $\forall$ $B(\bar{a},r)$ se tiene que $B(\bar{a},r)\cap A\neq\emptyset$ $\therefore$ $A\subset\bar{A}$

$Lema.$ Sea $A$ un subconjunto de $\mathbb{R}^n$

(1) Si $v\subset A$ y $v$ es abierto entonces $v\subset A^o$

$\small\textit{Demostración:}$ Sea $\bar{x}\in v$, como $v$ es abierto $\exists$ $r>0$ tal que $B(\bar{x},r)\subset v$ y como $v\subset A$ entonces $B(\bar{x},r)\subset A$ esto significa que $\bar{x}$ es un punto interior de $A$ es decir $\bar{x}\in A$.

(2) Si $A\subset F\subset\mathbb{R}^n$ y $F$ es cerrado, entonces $\bar{A}\subset F$

$\small\textit{Demostración:}$ Para probar que $\bar{A}\subset F$ mostraremos que el complemento de $F$, $F^c$ está contenido en el complemento de $\bar{A}^c$ de $\bar{A}$. Sea $\bar{x}\in F^c$ como $F$ es cerrado $F^c$ es abierto, luego $\exists$ $r>0$ tal que $B(\bar{x},r)\subset F^c$ pero $A\subset F$

$\therefore$ $F^c\subset A^c$ de donde $B(\bar{x},r)\subset
A^c$ o sea $B(\bar{x},r)\cap A=\emptyset$ esto significa que
$\bar{x}$ no es punto adherente de $A$ es decir $\bar{x}\not\in\bar{A}$ asi que $\bar{x}\in\bar{A}^c$.

$\textcolor{Red}{\textbf{Punto de Acumulación}}$

$\textbf{Ejemplo}$ Sea $A$ un subconjunto arbitrario de $\mathbb{R}^{n}$. Se dice que $\overline{x}\in \mathbb{R^{n}}$ es un \textit{\textbf{punto de acumulación}} de A, si toda bola abierta con centro en $\overline{x}$ contiene un punto de A distinto de $\overline{x}$ es decir $$\forall r>0 \quad \left(B(\overline{x},r)-{\overline{x}}\right)\bigcap A\neq \emptyset$$
Al conjunto de puntos de acumulación de A se le denomina el conjunto derivado de A y se le denota $A^{a}$

Sea $$A={(x,y)\in\mathbb{R}^{2}~|~x^{2}+y^{2}<1}=B((0,0),1)$$
Probaremos que el punto $$\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)$$
que no pertenece a $A$, es punto de acumulación de $A$.

Dado $r>0$ se tiene que
$$\left(\frac{1}{\sqrt{2}}-\frac{r}{\sqrt{2}(r+1)},\frac{1}{\sqrt{2}}-\frac{r}{\sqrt{2}(r+1)}\right)=\frac{1}{\sqrt{2}(r+1)}(1,1)$$
es tal que
$$\left|\frac{1}{\sqrt{2}}-\frac{r}{\sqrt{2}(r+1)},\frac{1}{\sqrt{2}}-\frac{r}{\sqrt{2}(r+1)}\right|=\frac{1}{\sqrt{2}(r+1)}|(1,1)|$$
$$=\frac{1}{\sqrt{2}(r+1)}\sqrt{2}$$
$$=\frac{1}{r+1}$$
$$<1$$

y por lo tanto pertenece a $A$. Por otra parte, se tiene que
$$0<\left|\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)-\left(\frac{1}{\sqrt{2}}-\frac{r}{\sqrt{2}(r+1)},\frac{1}{\sqrt{2}}-\frac{r}{\sqrt{2}(r+1)}\right)\right|$$
$$=\left|\frac{r}{\sqrt{2}(r+1)},\frac{r}{\sqrt{2}(r+1)}\right|$$
$$=\frac{r}{\sqrt{2}(r+1)}|(1,1)|$$
$$=\frac{r}{\sqrt{2}(r+1)}\sqrt{2}$$
$$=\frac{r}{r+1}$$
$$<r$$

de donde concluimos que este punto también pertenece al conjunto

$$B\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}},r\right)-\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)$$
y por lo tanto que
$$\left(B\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}},r\right)-\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)\right)\bigcap A\neq\empty$$
es decir, que
$$\left(\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)$$
es un punto de acumulación de $A$.

$\textbf{Ejemplo}$ Tenemos
$$A=(a,b)~\Rightarrow~A’=[a,b]$$
$$A=[0,1)-{2}~\Rightarrow~A’=[0,1]$$
$$A=\left\{\frac{1}{k}~\big|~k\in\mathbb{N}\right\}~\Rightarrow~A’=\left\{0\right\}$$