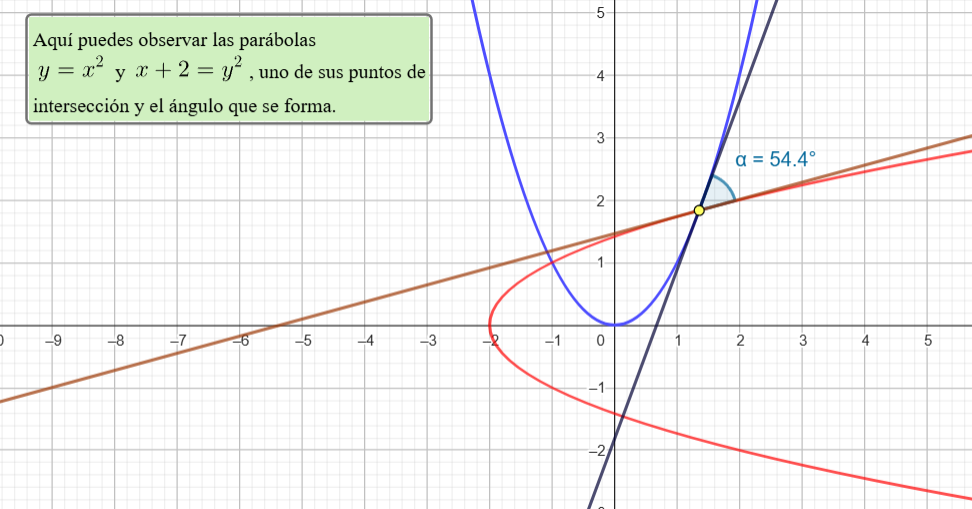
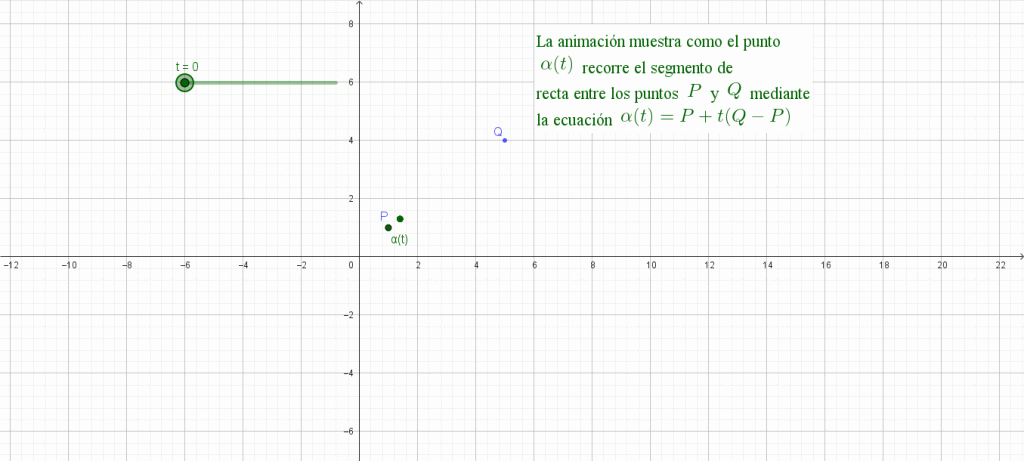
Sea $\alpha : I \subset \mathbb{R} \rightarrow \mathbb{R}^2$ una curva parametrizada por longitud de arco. Y supongamos ${\alpha}^{\prime \prime} (s_0) \neq \vec{0}.$
Sea $P =\alpha (s_0)$ y $Q = \alpha (s_1).$
Sea $m$ la mediatriz de $PQ$ y $n$ la recta normal a la curva en el punto $\alpha (s_0)$, la ecuación de $n$ es de la forma:
$$t \longrightarrow \overrightarrow{\alpha}(s_0) + t \, \overrightarrow{N}(s_0)$$
donde $\overrightarrow{N}(s_0) = \dfrac{{\alpha}^{\prime \prime} (s_0) }{\big\|{\alpha}^{\prime \prime} (s_0) \big\|}.$
Afirmación:
Cuando $s_1$ tiende a $s_0$ la recta $m$ se aproxima a la recta $n.$
$Q = \alpha (s_1) = (x(s_1), y(s_1))$
$P = \alpha (s_0) = (x(s_0), y(s_0))$
$R = $ punto medio $PQ = \Bigg(\dfrac{x(s_0)\, + \, x(s_1)}{2}, \dfrac{y(s_0)\, + \, y(s_1)}{2}\Bigg)$
Vector de dirección de $m $ ortogonal a $PQ$
$$PQ = \Big( – \, y(s_1)\, – \, y(s_0), x(s_1)\, – \, x(s_0) \Big)$$
La ecuación de $m$ es
$$ \Bigg( x \, – \, \dfrac{x(s_0)\, + \, x(s_1)}{2}, y \, – \, \dfrac{y(s_0)\, + \, y(s_1)}{2}\Bigg) \cdot \Bigg( x(s_1) \, – \, x(s_0), y(s_1) \, – \, y(s_0) \Bigg) = 0$$
Fijamos $s_0$ y dividimos todo entre $s_1 \, – \, s_0$
$$ \Bigg( x \, – \, \dfrac{x(s_0)\, + \ x(s_1)}{2}, y \, – \, \dfrac{y(s_0)\, + \, y(s_1)}{2}\Bigg) \cdot \Bigg( \dfrac{x(s_1) \, – \, x(s_0)}{s_1 \, – \, s_0}, \dfrac{y(s_1) \, – \, y(s_0)}{s_1 \, – \, s_0} \Bigg) = 0$$
Haciendo $s_1 \longrightarrow s_0$
$$\big(x \, – \, x(s_0), y \, – \, y(s_0) \big) \cdot \big(x'(s_0), y'(s_0) \big) = 0$$
donde esta última es la ecuación de $n.$
(1) Restringimos la búsqueda del centro de la circunferencia osculatriz a puntos en la recta normal a la curva en el punto $P = \alpha (s_0).$
Ecuación paramétrica de dicha recta
$$\big\{ \big(x(s_0), y(s_0) \big) + t \big( \, – \, y’ (s_0) , x’ (s_0) \big) \big| t \in \mathbb{R} \big\}$$
Buscamos un valor de $t$ en especial. $t^*$ tal que está en la intersección de las dos rectas normales y es de la forma
$$\big(x(s_0), y(s_0) \big) + t^* \big( \, – \, y’ (s_0) , x’ (s_0) \big) = \big(x(s_1), y(s_1) \big) + t^* \big( \, – \, y’ (s_1) , x’ (s_1) \big)$$
Veamos que pasa cuando $Q \rightarrow P$ es decir, cuando $s_1 \rightarrow s_0$
$ \big(x(s_0), y(s_0) \big) = P$ fijo.
$\big( \, – \, y’ (s_0) , x’ (s_0) \big)$ fijo.
solo varía $t$
¿Qué podemos decir de $t^*$ cuando $s_1 \rightarrow s_0$
Para responder a esta pregunta usamos la ecuación anterior para tener una expresión más «amigable» de $t^*.$
Tratamos de despejar $t^*$ en función de $s_0$ y $s_1.$
(2) Despejar $t^*$
$$ t^* \big( \, – \, y’ (s_0) , x’ (s_0) \big) \, – \, t^* \big( \, – \, y’ (s_1) , x’ (s_1) \big) = \big(x(s_1), y(s_1) \big) \, – \, \big( x(s_0), y(s_0) \big) $$
$$ t^* \Bigg(\dfrac{y’ (s_1) \, – \, y’ (s_0)}{s_1 \, – \, s_0}\Bigg) , \Bigg( \dfrac{(x’ (s_0) \, – \, x’ (s_1)}{s_1 \, – \, s_0}\Bigg) = \dfrac{(x(s_1) \, – \, x(s_0))}{s_1 \, – \, s_0} \, – \, \dfrac{(y(s_1) \, – \, y(s_0))}{s_1 \, – \, s_0} $$
Tomando el límite cuando $s_1 \longrightarrow s_0$, obtenemos que:
$\hat{t} ({y}^{\prime \prime} (s_0), – \, {x}^{\prime \prime} (s_0)) = \big(x’ (s_0), {y \, }’ (s_0) \big)$
Multiplicando por $ \big( {x}^{\prime} (s_0), {y}^{\prime} (s_0) \big)$
$$ \hat{t} \big(x’ (s_0) {y}^{\prime \prime} (s_0) \, – \, {y}^{\prime} (s_0) {x}^{\prime \prime} (s_0) \big) = 1$$
Por lo tanto
$$ \hat{t} = \dfrac{1}{ \big( x’ (s_0) {y}^{\prime \prime} (s_0) \, – \, {y}^{\prime} (s_0) {x}^{\prime \prime} (s_0) \big) }$$
es el radio de la circunferencia osculatriz.
Sin pérdida de generalidad; si la curva está parametrizada de tal forma que ${\alpha}^{\prime \prime} (s_0) = \big({x}^{\prime \prime} (s_0), {y}^{\prime \prime} (s_0) \big) = \mathcal{K}(s_0) \big(\, – \, {y}^{\prime} (s_0) , {x}^{\prime} (s_0) \big)$ con $\mathcal{K} (s_0) > 0.$
En tal caso, $\big\|{\alpha}^{\prime \prime} (s_0) \big\| = \mathcal{K} (s_0)$ es la curvatura.
$\Biggr|\begin{matrix} {x}^{\prime} (s_0) & {x}^{\prime \prime} (s_0) \\ {y}^{\prime} (s_0) & {y}^{\prime \prime} (s_0) \end{matrix} \Biggr| = {x}^{\prime} {y}^{\prime \prime} \, – \ {y}^{\prime} {x}^{\prime \prime} = \dfrac{1}{\mathcal{K}}$
En el siguiente enlace puedes observar una animación de los conceptos trabajados aplicados a una caso particular.
https://www.geogebra.org/classic/bppzcxq6