Introducción

En este apartado se abordará uno de los temas más típicos que nos podemos encontrar dentro de las matemáticas financieras, y se caracteriza por ser uno de los temas que comienzan a combinar las reglas, en el sentido de que vamos a utilizar variantes que hasta el momento no se habían utilizado, como lo es que la periodicidad de la tasa de interés no va a coincidir con la que se está manejando en el tipo de pagos, motivo por el que se tendrá que utilizar un tipo de tasa equivalente. Sin embargo, como se verá más adelante, siempre va a ser posible encontrar una tasa efectiva que logre resolver éste problema. Uno de los principales objetivos de este tipo de anualidad es explicar de forma sencilla la forma en que se puede amortizar un crédito.

Descripción general

Este tipo de anualidad tiene como punto de partida una cantidad que debe de cubrirse durante justamente un año, dicha cantidad deberá de ser la misma durante los años que siguen, hasta que se haya pagado la totalidad de la deuda que se haya adquirido. Su principal característica consiste en que se defina el número de veces $p$ en que serán realizados los pagos durante el año, lo anterior quiere decir que dicha cantidad anual será dividida entre $p$ para obtener la cifra que será pagada cada p-ésimo año. Por ejemplo, si un contrato de crédito estipula que la deuda será pagada con anualidades de \$24,000 pagaderos mensualmente, esto significa que cada mes se realizará un pago de \$2,000 durante los 12 meses que tiene dicho año. Este tipo de anualidades son muy parecidas al tema de tasas nominales, las cuales coinciden con la misma característica de ser pagaderas $m$ veces al año.

Vale la pena recordar que las tasas nominales, se obtienen de dividir una tasa nominal entre $m$. Por lo que de forma similar se pueden calcular este tipo de anualidades, sólo que la cantidad que se pretende pagar durante el año, es una referencia y cada uno de los $p$-ésimos es la cantidad real que se va a pagar, además de que serán estás cantidades la que se utilizarán cuando se quiera calcular su valor presente.

Al hacer uso de este tipo de anualidades se pueden tener las siguientes variaciones:

• Del tipo de anualidad en el que la periodicidad de la tasa sea menor a la del periodo de cada pago.
• Cuando el periodo del pago sea igual al de la tasa.
• Cuando la periodicidad de la tasa sea mayor que la del pago.

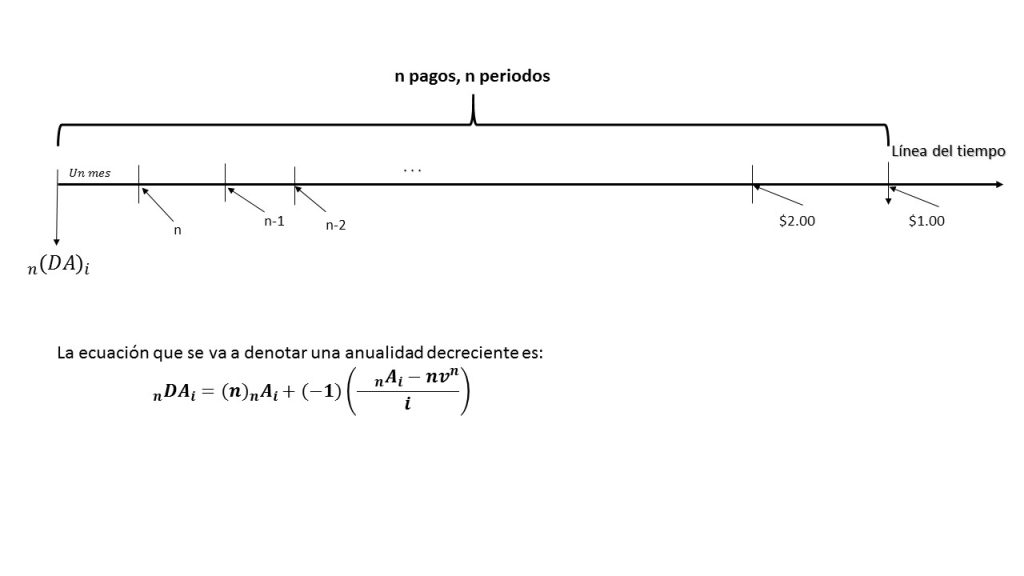
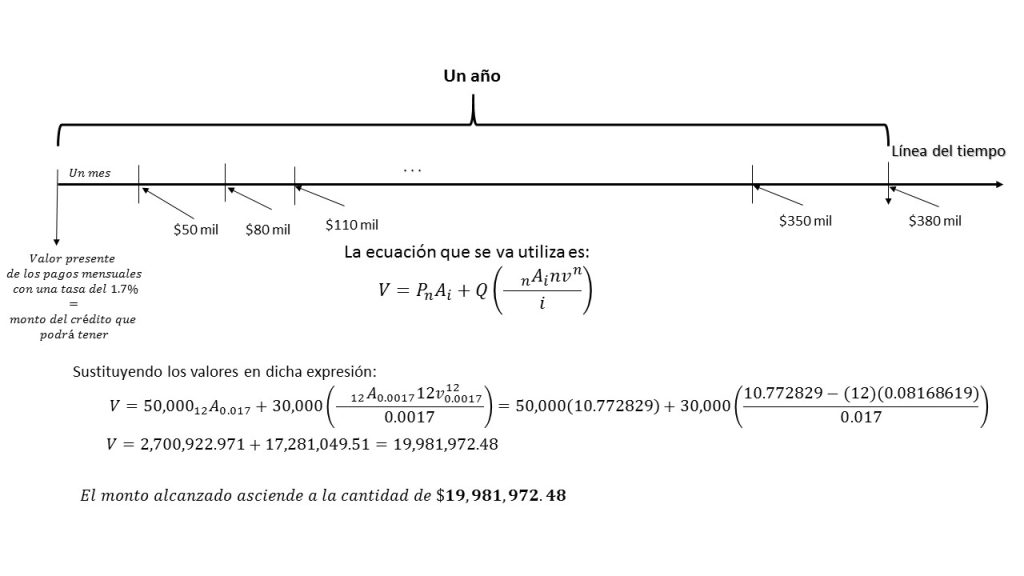
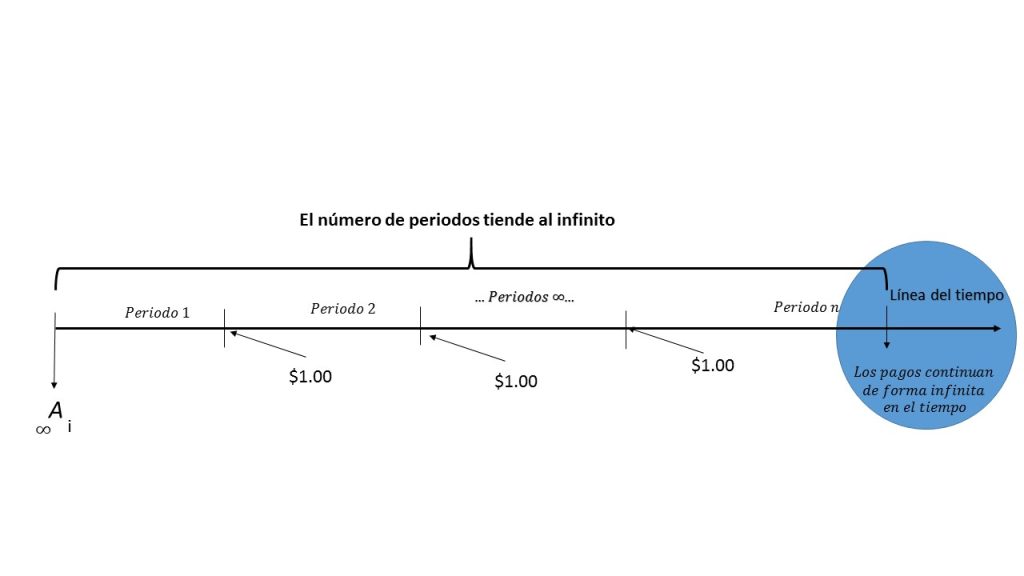
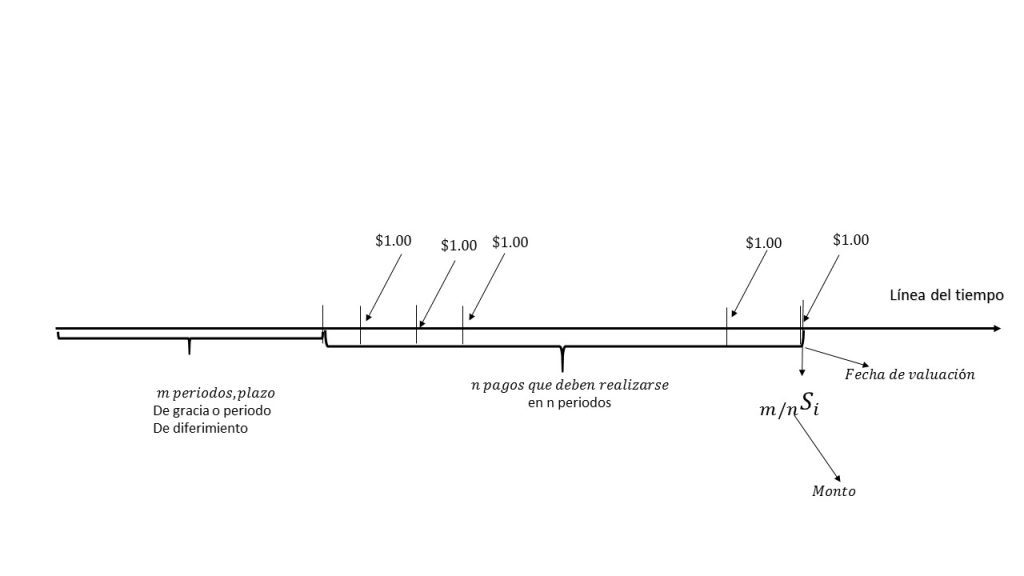
La siguiente gráfica nos muestra el comportamiento de este tipo de anualidad:

La imagen muestra el comportamiento de una anualidad pagadera p veces al año, la cual será denotada por:

$$\prescript{}{n(p)}{\mathbf{A}}_i$$

donde:

• $n$ es la cantidad de años que se pactó, en los cuales se va a realizar el pago del crédito.
• $p$ es la cantidad de veces que la anualidad será pagadera en un año.
• $i$ es la cantidad de interés, que en particular para este tipo de anualidades, no será precisamente efectiva por $p$-ésimo cada periodo.

Valor presente con tasa de interés efectiva anual

Para obtener el valor presente de este tipo de anualidades, haciendo los cálculos con un capital de \$1 peso, a una tasa de interés efectiva anual $i$, se hace lo siguiente:

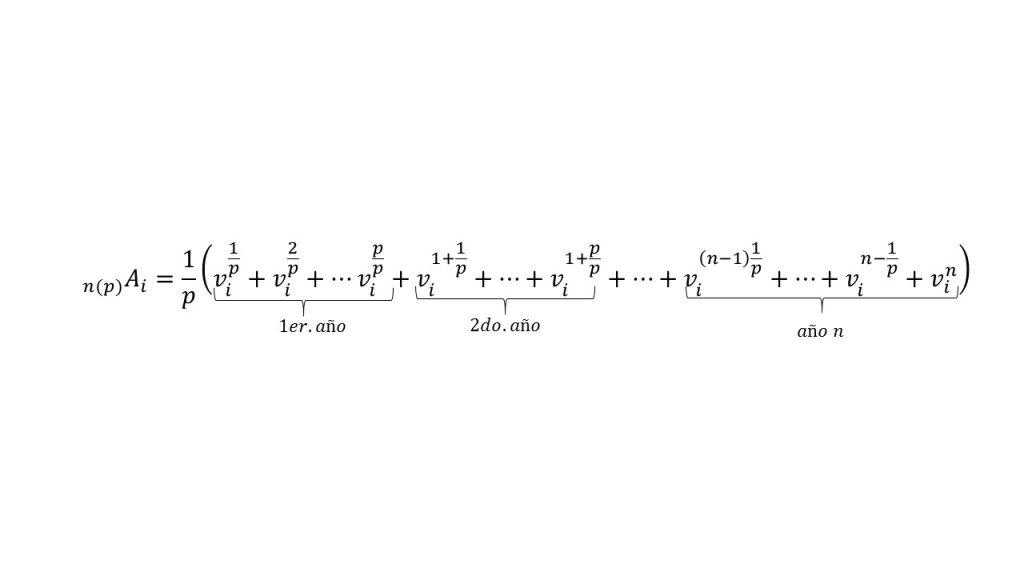
Reduciendo términos nos queda:

$$\prescript{}{n(p)}{\mathbf{A}}_i=\frac{1}{p}\left(v_i^{\frac{1}{p}}+v_i^{\frac{2}{p}}+…+v_i^{\frac{p}{p}}+v_i^{1+\frac{1}{p}}+…+v_i^2+…+v_i^{(n-1)+\frac{1}{p}}+…+v_i^{n-\frac{1}{p}}+v_i^n\right).$$

Como el resultado que se acaba de obtener. está siendo multiplicado por una progresión geométrica entonces:

$$\prescript{}{n(p)}{\mathbf{A}}_i=\frac{1}{p}\left(\frac{v_i^{\frac{1}{p}}-v_i^nv_i^{\frac{1}{p}}}{1-v_i^{\frac{1}{p}}}\right)$$

luego factorizando a $v_i^{\frac{1}{p}}$:

$$\prescript{}{n(p)}{\mathbf{A}}_i=\frac{1}{p}\left(\frac{v_i^{\frac{1}{p}}(1-v_i^n)}{1-v_i^{\frac{1}{p}}}\right).$$

Ahora multiplicando por el número 1, pero expresado como $\frac{(1+i)^{\frac{1}{p}}}{(1+i)^{\frac{1}{p}}}$ se obtiene:

$$\prescript{}{n(p)}{\mathbf{A}}_i=\frac{1}{p}\left(\frac{(1+i)^{\frac{1}{p}}v_i^{\frac{1}{p}}(1+v_i^n)}{(1+i)^{\frac{1}{p}}(1-v_i^{\frac{1}{p}})}\right).$$

Nótese que $v=\frac{1}{1+i}$, luego entonces:

$$\prescript{}{n(p)}{\mathbf{A}}_i=\frac{1}{p}\left(\frac{(1-v_i^n)}{(1+i)^{\frac{1}{p}}-1}\right).$$

Luego, por la triple igualdad se tiene:

$$(1+i)^{\frac{1}{p}}=\left(1+\frac{i^{(p)}}{p}\right)^1.$$

Sustituyendo dicha expresión se tiene:

$$\prescript{}{n(p)}{\mathbf{A}}_i=\frac{1}{p}\left(\frac{(1-v_i^n)}{\left(1+\frac{1^{(p)}}{p})\right)-1}\right)$$

$$\prescript{}{n(p)}{\mathbf{A}}_i=\frac{1-v_i^n}{p+i^{(p)}-p}.$$

Reduciendo la expresión queda:

$$\prescript{}{n(p)}{\mathbf{A}}_i=\frac{1-v_i^n}{i^{(p)}}$$

ésta expresión puede escribirse en términos de $\prescript{}{n}{\mathbf{A}}_i$ al mulitplicar el lado derecho por $\frac{i}{i}$:

$$\prescript{}{n(p)}{\mathbf{A}}_i=\frac{i}{i^{(p)}}\left(\frac{1-v_i^n}{i}\right)$$

recordando que $\prescript{}{n}{\mathbf{A}}_i=\left(\frac{1-v_i^n}{i}\right)$ se obtiene:

$$\prescript{}{n(p)}{\mathbf{A}}_i=\frac{i}{i^{(p)}}\prescript{}{n}{\mathbf{A}}_i.$$

Por otra parte, para obtener el valor presente de ésta anualidad, es necesario calcular una tasa efectiva por $p$-ésimo, así como una $i’$, que sea equivalente efectiva anual, para lograrlo se hace lo siguiente:

$$(1+i)^{\frac{1}{p}}=\left(1+\frac{i^{(p)}}{p}\right)^1=(1+i’)$$

$$i’=\frac{i^{(p)}}{p}=(1+i)^{\frac{1}{p}}-1.$$

Usando la tasa que se acaba de obtener, se puede calcular la anualidad a $n$ años, pagadera $p$ veces al año, como una anualidad vencida de $np$ pagos de $1/p$ (que significa $p$ pagos al año, aplicados por $n$ años). El valor presente de dicha anualidad queda denotado por la expresión:

$$\prescript{}{n(p)}{\mathbf{A}}_{i’}=\frac{1}{p}\prescript{}{n+p}{\mathbf{A}}_{i’}.$$

Como $\prescript{}{n}{\mathbf{A}}_i=\frac{1-v_i^n}{i}$ se tiene:

$$\prescript{}{n(p)}{\mathbf{A}}_{i’}=\frac{1}{p}\prescript{}{n+p}{\mathbf{A}}_{i’}=\frac{1}{p}\left(\frac{1-v_{i’}^{np}}{i’}\right).$$

Observación, para el cálculo de todas éstas expresiones se utilizó un capital de \$1 peso, entonces al cambiar dicho valor por uno $X$, la expresión obtenida del valor presente queda como:

$$V=X\prescript{}{n(p)}{\mathbf{A}}_{i’}=\frac{X}{p}\prescript{}{np}{\mathbf{A}}_{i’}.$$

Otro método para encontrar el valor presente de una anualidad pagadera $p$ veces al año con una tasa de interés efectiva anual, es calculando el monto al final del año, y de los pagos $p$, $1/p$ que se realizan durante dicho año.

Lo anterior se traduce en la siguiente expresión:

$$X=\frac{1}{p}\left((1+i)^{1-\frac{1}{p}}+(1+i)^{1-\frac{2}{p}}+…+(1+i)^{\frac{1}{p}}+1\right).$$

Reduciendo términos al efectuar las sumas, se obtiene:

$$X=\frac{1}{p}\left(\frac{1-(1+i)^{1-\frac{1}{p}}(1+i)^{\frac{1}{p}}}{1-(1-i)^{\frac{1}{p}}}\right)=\frac{1}{p}\left(\frac{1-(1+i)^1}{1-(1+i)^{\frac{1}{p}}}\right).$$

Como $(1+i)^{\frac{1}{p}}=\left(1+\frac{i^{(p)}}{p}\right)^1$

luego entonces:

$$X=\frac{1}{p}\left(\frac{1-(1+i)^1}{1-\left(1+\frac{i^{(p)}}{p}\right)}\right)=\frac{1}{p}\left(\frac{1-(1+i)}{\frac{i^{(p)}}{p}}\right)=\frac{p}{p}\left(\frac{1-(1+i)}{i^{(p)}}\right)=\frac{i}{i^{(p)}}.$$

Lo que se acaba de obtener nos dice que el pago anual es equivalente a la suma de los $p$ pagos de $1/p$, que se realizan en el año, los cuales son acumulados con una tasa de interés efectiva anual, observe que la suma aritmética de cada uno de ellos es igual a uno.

Finalmente, la expresión del valor presente de una anualidad pagadera p veces al año es:

$$\prescript{}{n(p)}{\mathbf{A}}_i=\frac{i}{i^{(p)}\prescript{}{n}{\mathbf{A}}_i}$$

El resultado que es igual al que previamente se había obtenido previamente con el otro método.

Por último, se va a cambiar el capital de \$1 peso, por un capital$X$, y la expresión queda:

$$V=X\prescript{}{n(p)}{\mathbf{A}}_i=X\frac{i}{i^{(p)}\prescript{}{n}{\mathbf{A}}_i}.$$

Las anualidades pagaderas $p$ veces al año, se resuelven calculando una tasa efectiva equivalente por periodo de pago, aplicando el modelo de anualidades vencidas, considerando que los pagos se realizan $p$ veces de $1/p$ cada año.

Observación: para calcular una anualidad pagadera $p$ veces al año, con una tasa nominal de interés, sólo es necesario calcular la tasa equivalente por periodo de pago, haciendo uso del modelo de anualidades vencidas, tomando en consideración que realizan $p$ pagos de $1/p$ de forma anual.

Monto

Para calcular el monto de este tipo de anualidades, se va a obtener partiendo de un capital de \$1 peso, para luego obtener su valor presente por $n$ periodos con una tasa efectiva anual, o durante $np$ periodos en el caso de que la tasa sea efectiva por cada periodo de pago.

Para el primer supuesto, se utiliza la siguiente ecuación:

$${\prescript{}{(n)(p)}{\mathbf{S}}_{i}}=\frac{i}{i^{(p)}}{\prescript{}{n}{\mathbf{A}}_{i}}(1+i)^n.$$

Para el segundo supuesto, se utilizará:

$${\prescript{}{(n)(p)}{\mathbf{S}}_{i’}}=\frac{1}{p}{\prescript{}{(n)}{\mathbf{A}}_{i’}}(1+i)^{n*p}.$$

Por último, se realizará el cambio del capital que fue de un peso por el monto \$X, lo que hace que las dos ecuaciones queden de la siguiente forma:

$$M=X\prescript{}{n(p)}{\mathbf{S}}_i=X\frac{i}{i^{(p)}}\prescript{}{n}{\mathbf{A}}_i(1+i)^n$$

$$M=X\prescript{}{n(p)}{\mathbf{S}}_{i’}=\frac{X}{p}\prescript{}{n+p}{\mathbf{A}}_{i’}(1+i’)^{n+p}$$

Ejercicios resueltos

Ejercicio. Una empresa de mantenimiento de maquinaria pesada para la construcción, necesita un crédito para modernizar su planta, por una cantidad de \$120 mil. El banco con el que está realizando dicho préstamo, le ofrece que lo pague en dos años, con pagos semanales a una tasa de interés efectiva anual del 15%. Se necesita saber ¿cuánto se pagara cada semana?

Ejercicio. La empresa COPPEL vende articulos para el hogar, entre los que destacan electrodomésticos, ropa, muebles, etc. Una familia desea adquirir una sala, el valor de ésta asciende a \$40,000, si al solicitar el crédito aportan un enganche de \$10 mil pesos, y el resto lo pagan a crédito. ¿Cuánto es lo que deben de pagar cada mes, si la tasa de interés que les están cobrando es del 35% pagadero mensual.

Más adelante…

Hasta este momento se han estado analizando varios tipos de anualidades, y como bien se podrá observar, las combinaciones entre ellas cada vez es mayor, lo que implica con ello, un mayor grado de dificultad, sobre todo cuando se esté trabajando con tasas equivalentes, en las que muchas veces sólo se deja indicada la operación, sin embargo es necesario tener muy en cuenta que ésos cálculos no deben de ser olvidados. En los temas siguientes se irán abordando más tipos de anualidades, en particular las que son del tipo continuas.

Entradas relacionadas

• Ir a Matemáticas Financieras
• Entrada anterior
• Entrada siguiente

Introducción

En éste apartado, se abordarán las anualidades opuestas a las que acabamos de revisar, las anualidades decrecientes, las cuales como su nombre lo indica su principal característica es que conforme avanza el tiempo van disminuyendo. Su uso se presenta en los casos en los que se otorga un préstamo, un crédito, en el que el bien adquirido con el paso del tiempo se va deteriorando, es decir, cuando están nuevos y recién adquiridos requieren un mantenimiento mínimo, sin embargo con el paso del tiempo y el uso, van necesitando cada vez mantenimientos más costosos, y si a ello se le agrega que aún no se terminan de pagar, pues este tipo de anualidad se amolda muy bien a ésta situación, en la que el deudor le conviene bastante que en el momento en el que se requieran servicios más costosos, se pague cada vez menos a la deuda adquirida, sin que por ello se omita o incumpla alguna obligación. Todo este acuerdo, se pacta desde un inicio entre las partes involucradas.

Descripción y valor presente

Una anualidad decreciente, es aquella que conforme avanza el tiempo, los pagos que se van realizando cada vez son menores, el objetivo de este tipo de anualidad es que la persona deudora este en las condiciones de poder cumplir cómodamente con sus obligaciones, al mismo tiempo que la institución que otorga el crédito o préstamo no vea afectado la recuperación de sus recursos ni asuma un riesgo mayor.

Éste tipo de anualidad, tiene como característica principal que cada pago realizado es igual al anterior menos una cierta cantidad. Otra característica importante es que comienza con un pago de cierto valor, llamémoslo $n$ y los pagos siguientes van a ir disminuyendo una cierta cantidad, hasta llegar al último pago con valor igual a un peso.

El valor presente de esta anualidad se denota por:

$$\prescript{}{n}{\mathbf{(DA)}}_i$$

donde:

• $D$ hace referencia a la palabra decreasing (decreciente).
• $n$ es el número de pagos que se van a realizar.
• $i$ continúa representando la tasa de interés efectiva por periodo.

Para obtener el valor presente de dicha anualidad, se partirá de la siguiente expresión:

$$\prescript{}{n}{\mathbf{(DA)}}_i=(n)\prescript{}{n}{\mathbf{A}}_i+(-1)\left(\frac{\prescript{}{n}{\mathbf{A}}_i-nv^n}{i}\right).$$

Luego:

$$\prescript{}{n}{\mathbf{(DA)}}_i=\frac{in\prescript{}{n}{\mathbf{A}}_i-\prescript{}{n}{\mathbf{A}}_i+nv^n}{i}.$$

Recordando, que $\prescript{}{n}{\mathbf{A}}_i=\frac{1-v^n}{i}$, la expresión anterior se convierte en:

$$\prescript{}{n}{\mathbf{(DA)}}_i=\frac{in\left(\frac{1-v^n}{i}\right)-\prescript{}{n}{\mathbf{A}}_i+nv^n}{i}.$$

Luego, cancelando las $i$ del numerador y multiplicando por $n$ la expresión que está entre paréntesis, se obtiene:

$$\prescript{}{n}{\mathbf{(DA)}}_i=\frac{n(1-v^n)-\prescript{}{n}{\mathbf{A}}_i+nv^n}{i}=\frac{n-nv^n-\prescript{}{n}{\mathbf{A}}_i+nv^n}{i}.$$

Por último, reducimos términos:

$$\prescript{}{n}{\mathbf{(DA)}}_i=\frac{n-\prescript{}{n}{\mathbf{A}}_i}{i}.$$

Para generalizar la expresión, se toma como primer pago a $P$ y los pagos siguientes disminuyen una cantidad $Q$, pero se debe de tener cuidado con el último pago, $P-(n-1)Q$, sea positivo; esto es que $P$ debe ser mayor a $(n-1)Q.$

Entonces, la ecuación para calcular el valor presente seria:

$$V=P\prescript{}{n}{\mathbf{A}}_i-Q\left(\frac{\prescript{}{n}{\mathbf{A}}_i-nv^n}{i}\right).$$

Monto

El monto de una anualidad decreciente, con $n$ pagos que se aportarán durante $n$ periodos, fijando el primer pago $n$ y los pagos siguientes irán disminuyendo en una unidad, se calcula de forma similar a los crecientes, y es denotada por:

$$\prescript{}{n}{\mathbf{SD}}_i=\frac{n-\prescript{}{n}{\mathbf{A}}_i}{i}(1+i)^n.$$

En este tipo de anualidad decreciente, el primer pago será $P$ mientras que los pagos siguientes serán disminuidos por una cantidad $-Q$, la expresión queda denotada por:

$$V=P\prescript{}{n}{\mathbf{A}}_i(1+i)^n-Q\left(\frac{\prescript{}{n}{\mathbf{A}}_i-nv^n}{i}\right)(1+i)^n.$$

Por último, el monto de una anualidad geométrica decreciente con razón $(1-K)$ es:

$$V=X\left(1-\frac{(1-k)^n}{(1+i)^n}\right)\left(\frac{(1+i)^n}{1+k}\right).$$

Ejercicios resueltos

Ejercicio. Una empresa de aeronaves, necesitan refacciones para sus aviones, sus socios desean adquirir un crédito para ello, y planean pagarlo con aportaciones decrecientes, las cuales están basadas en su experiencia de ingresos. Al hacer sus cálculos, llegan a la conclusión de que cada uno de sus socios pueden realizar aportaciones mensuales de forma vencida, comenzando con un adelanto de \$6 mil pesos, disminuyendo los siguientes pagos en \$250, hasta llegar a mensualidades de \$2 mil. Pretenden, además, negociar, para que el banco les otorgue un plazo para pagar su crédito de 2 años, a una tasa de interés del 10.5% pagadero mensual el banco les otorga una plazo de año y medio. ¿Se necesita saber qué cantidad es la que el banco puede prestar a cada uno de sus socios?

Ejercicio. Una empresa de restaurantes, desea abrir una sucursal en el pueblito abc, para llevarlo a cabo ha considerado una inversión de \$250 mil pesos. El dueño en base a su experiencia, aspira a tener ingresos de la siguiente forma:

• Considera poder hacerse de clientes durante los primeros 2 años, por lo que calcula tener ingresos en el primer mes de cada periodo de \$3000 pesos, los cuales irán incrementando \$800 pesos cada periodo durante los meses restantes (23 meses).
• Espera que las ventas se mantengan estables en los 2 años que siguen, ingresos de \$6 mil
• En el último año considera tener ingresos de \$7 mil pesos, con una posible caída de ventas de \$200 pesos mensuales hasta el término de dicho año.

Si el dueño de ése restaurante, espera recuperar su inversión de \$250 mil pesos valuados a la fecha de apertura, así como tener una ganancia de 25% anual. ¿Se necesita saber si con los datos que él dueño planeó, es suficiente para alcanzar sus metas, sobre todo si se propone tener ganancias netas del 35%.

Más adelante…

Se abordarán las anualidades pagaderas p veces al año, las cuales son de gran utilidad cuando se tiene casos en los que lo que se pretende es dar una expresión clara de cómo se puede ir pagando un crédito, conociendo la cantidad que se debe de pagar en cada periodo. Con este tema terminamos de adquirir las herramientas necesarias para poder evaluar proyectos de inversión.

Entradas relacionadas

• Ir a Matemáticas Financieras
• Entrada anterior
• Entrada siguiente

Introducción

Este tipo de anualidades se utiliza en los casos en lo que alguien solicita un crédito, y de alguna forma sabe que en el futuro sus ingresos mejorarán, condición que les permitirá poder cada vez dar mayores cantidades, para pagar dicho crédito. Un ejemplo de lo anterior, es cuando una empresa moderniza su maquinaria, y al hacerlo esto le da la condición de poder tener una mayor producción, lo cual genera mayores ingresos, mayor venta y por consecuencia mayores utilidades, las cuales pueden irse incrementando y a través de ellas, logrando con esto, aportar una mayor cantidad para liquidar su deuda.

Descripción y valor presente

Se define como anualidad creciente, al tipo de anualidad que se caracteriza por ir incrementando los pagos en cada periodo, es decir; cada pago se realiza con una cantidad mayor, de manera que los pagos crecerán de forma aritmética. Dichos incrementos son acordados entre las partes involucradas, de acuerdo con la capacidad de pago que tenga el deudor, los cuales estarán basados a partir de los cálculos de sus ingresos futuros.

La imagen anterior, muestra gráficamente el comportamiento de una anualidad creciente, así como la forma, en que se convierte en una progresión aritmética.

Si se quiere calcular el valor presente, $V$, en una anualidad creciente, es necesario traer a valor presente cada uno de los pagos, considerando una tasa de interés efectiva por periodo. Esto se puede observar en la siguiente expresión:

$$V=Pv+(P+Q)v^2+(P+2Q)v^3+(P+3Q)v^4+…+[P+(n-2)Q]^{n-1}+[P+(n-1)Q]v^n.$$

Para obtener una expresión más sencilla, se resolverán los productos indicados, es decir:

$$V=Pv+Pv^2+Qv^2+Pv^3+2Qv^3+..+Pv^{n-1}+(n-2)Qv^{n-1}+Pv^n+(n-1)Q^{n}.$$

Ahora, se multiplicará la ecuación, por un uno, de la siguiente forma:

$$1=\left(\frac{1+i}{1+i}\right)$$

aplicándolo a la expresión que teníamos, da como resultado:

$$\left(\frac{v^1}{v^1}\right)V=Pv+Pv^2+Qv^2+Pv^3+2Qv^3+..+Pv^{n-1}+(n-2)Qv^{n-1}+Pv^n+(n-1)Q^{n}$$

$$\left(\frac{(1+i)^1}{(1+i)^1}\right)V=Pv+Pv^2+Qv^2+Pv^3+2Qv^3+..+Pv^{n-1}+(n-2)Qv^{n-1}+Pv^n+(n-1)Q^{n}$$

$$(1+i)V=[Pv+Pv^2+Qv^2+Pv^3+2Qv^3+..+Pv^{n-1}+(n-2)Qv^{n-1}+Pv^n+(n-1)Q^{n}](1+i)^{-1}$$

$$V+iV=Pvv^{-1}+(P+Q)v^2v^{-1}+(P+2Q)v^3v^{-1}+…+[P+(n-2)Q]v^{n-1}v^{-1}+[P+(n-1)Q]v^nv^{-1}$$

$$V+iV=P+(P+Q)v^1+(P+2Q)v^2+…+[P+(n-2)Q]v^{n-2}+[P+(n-1)Q]v^{n-1}$$

$$V+iV=P+Pv+Qv+P^2+2Qv^2+…+Pv^{n-2}+(n-2)Qv^{n-2}+Pn^{n-1}+(n-1)Qv^{n-1}.$$

Restando ésta última expresión, con la segunda que obtuvimos se tiene:

$$V+iV=P+Pv+Qv+P^2+2Qv^2+…+Pv^{n-2}+(n-2)Qv^{n-2}+Pn^{n-1}+(n-1)Qv^{n-1}$$

$$-V=-Pv-Pv^2-Qv^2-Pv^3-2Qv^3-…-Pv^{n-1}-(n-2)Qv^{n-1}-Pv^n-(n-1)Q^{n}.$$

Nos da como resultado:

$$iV=P+Qv+Qv^2+Qv^3+…+Qv^{n-1}-Pv^n-(n-1)Qv^n.$$

Haciendo las multiplicaciones indicadas, se obtiene:

$$iV=P+Qv+Qv^2+Qv^3+…+Qv^{n-1}+Qv^n+Pv^n-nQv^n.$$

Factorizando $Q$ se tiene:

$$iV=P+Q(v+v^2+v^3+…+v^{n-1}+v^{n})-Pv^n-nQv^n.$$

Factorizando ahora a $P$:

$$iV=P(1-v^n)+Q\prescript{}{n}{\mathbf{A}}_i-nQv^n$$

lo anterior, ocurre porque $\prescript{}{n}{\mathbf{A}}_i= v+v^2+v^3+…+v^{n-1}+v^{n}$

de donde, se despeja a $V$ para obtener:

$$V=P\left(\frac{1-v^n}{i}\right)+Q\left(\frac{\prescript{}{n}{\mathbf{A}}_i-nv^n}{i}\right).$$

Tomando en cuenta que $\prescript{}{n}{\mathbf{A}}_i=\frac{(1-v^n)}{i}$, y sustituyendo dicho valor en la ecuación anterior, se tiene por fin la expresión más sencilla para el cálculo del valor presente de una anualidad creciente con $n$ pagos:

$$V=P\prescript{}{n}{\mathbf{A}}_i+Q\left(\frac{\prescript{}{n}{\mathbf{A}}_i-nv^n}{i}\right).$$

En la imagen, se muestra el comportamiento de una anualidad creciente ordinaria, en la que el capital (P), que se está manejando, así como el incremento (Q), se tomaron por igual a un peso. De dicho supuesto, la ecuación nos queda como sigue:

$P=Q=1$

$$\prescript{}{n}{\mathbf{IA}}_i=(1)\prescript{}{n}{\mathbf{A}}_i+(1)\left(\frac{\prescript{}{n}{\mathbf{A}}_i-nv^n}{i}\right)$$

de donde, sacando a $i$ como común denominador se tiene:

$$\prescript{}{n}{\mathbf{IA}}_i=\frac{i\prescript{}{n}{\mathbf{A}}_i+\prescript{}{n}{\mathbf{A}}_i-nv^n}{i}.$$

Reagrupando términos:

$$\prescript{}{n}{\mathbf{IA}}_i=\frac{\prescript{}{n}{\mathbf{A}}_i+\frac{i(1-v^n)}{i}-nv^n}{i}.$$

Reduciendo y reordenando términos:

$$\prescript{}{n}{\mathbf{IA}}_i=\frac{\prescript{}{n}{\mathbf{A}}_i-v^n+1-nv^n}{i}.$$

Por último, se hace el recordatorio que:

$$\prescript{}{n-1}{\mathbf{A}}_i=\prescript{}{n}{\mathbf{A}}_i-v^n$$

sustituyendo el recordatorio en la ecuación que se venía desarrollando, se tiene por fin la expresión más sencilla para calcular el valor presente de una anualidad creciente ordinaria:

$$\prescript{}{n}{\mathbf{IA}}_i=\frac{\prescript{}{n-1}{\mathbf{A}}_i+1-nv^n}{i}.$$

De la misma forma que, con los modelos obtenidos anteriormente, haciendo despejes, se puede obtener cualquier variable que se utilice en ésa ecuación para conocer su valor numérico. Dentro del modelo que se acaba de obtener, es importante señalar que:

$P$ es el primer pago, no se le llamo $X$ para poder diferenciarlo de que los pagos dentro de las anualidades crecientes, van a ser diferentes cada uno de ellos.

Monto

Los montos en una anualidad creciente son denotados por:

$$\prescript{}{n}{\mathbf{SV}}_i.$$

En la gráfica, se muestra el comportamiento del monto en una anualidad creciente, en la que se exhibe que el primer pago es denotado como $P$ y los pagos siguientes son representados por la letra $Q$, luego $2Q$, $3Q$, sucesivamente hasta llegar al valor $(n-1)Q$.

El monto, se calcula al tomar el valor presente de dicha anualidad, y se acumula durante $n$ periodos a la misma tasa de interés, esto se traduce en la siguiente expresión:

$$\prescript{}{n}{\mathbf{(SV)}}_i=\left(P\prescript{}{n}{\mathbf{A}}_i+Q\left(\frac{\prescript{}{n}{\mathbf{A}}_i-nv^n}{i}\right)\right)(1+i)^n.$$

Efectuando los productos indicados se tiene:

$$\prescript{}{n}{\mathbf{(SV)}}_i=P\prescript{}{n}{\mathbf{A}}_i(1+i)^n+Q\left(\frac{\prescript{}{n}{\mathbf{A}}_i(1+i)^n-nv^n(1+i)^n}{i}\right).$$

Por otra parte, como:

$$\prescript{}{n}{\mathbf{(SV)}}_i=\prescript{}{n}{\mathbf{(A)}}_i(1+i)^n$$

además de que, $v^n=(1+i)^n$, y sustituyendo dicho valor en la ecuación anterior resulta:

$$\prescript{}{n}{\mathbf{(SV)}}_i=P\prescript{}{n}{\mathbf{S}}_i+Q\left(\frac{\prescript{}{n}{\mathbf{S}}_i-n}{i}\right).$$

Ésta, es la expresión más simplificada para obtener el monto de una anualidad creciente, con primer pago $P$ y pago siguiente $Q$ el cual se incrementa en cada periodo a una tasa de interés efectiva por periodo.

De forma semejante a como se ha venido haciendo, suponemos que $P=Q=1$, entonces se obtiene de forma sencilla la siguiente expresión:

$$\prescript{}{n}{\mathbf{(SV)}}_i=\frac{\prescript{}{n-1}{\mathbf{A}}_i+1-nv^n}{i}(1+i)^n$$

que corresponde a una anualidad creciente ordinaria, lo que es también equivalente a la siguiente expresión:

$$\prescript{}{n}{\mathbf{(SV)}}_i=\prescript{}{n}{\mathbf{S}}_i+\left(\frac{\prescript{}{n}{\mathbf{S}}_i-n}{i}\right).$$

Ejercicios resueltos

Ejercicio. Una empresa quiere modernizar su maquinaria, para ello se propone adquirir un crédito. El costo de la maquinaria asciende a un valor de \$1,500,000. Una vez adquirida e instalada, se estima que su producción se incrementará de la siguiente forma: \$30,000 fijos mensuales, con un crecimiento de \$10,000 para las siguientes mensualidades. Tomando en cuenta que la institución financiera que otorgó el préstamo, le da un plazo de un año para liquidar dicha deuda a una tasa de interés de 1.7% mensual, se desea saber ¿de cuánto será el crédito para solventar proyecto?

El señor Abel, quiere constituir una reserva para hacer frente a posibles emergencias que puedan presentarse, con la finalidad de no verse afectado en su economía cuando lleguen a ocurrir. Por tal motivo, quiere ahorrar su aguinaldo que recibió este año junto con sus prestaciones, las cuales en total ascienden a una cantidad de \$15 mil pesos, y planea hacer aportaciones por mil pesos, cantidad que quiere incrementar en \$100 pesos cada mes. Desea saber ¿cuánto dinero puede ahorrar?, si mantiene ésta forma de ahorro durante 1 año, y el banco en que mantiene sus ahorros le ofrece una tasa de interés del 2.9% mensual.

Más adelante…

Se continuará abordando el concepto de anualidad, ahora en su forma decreciente, en la que se analizará las situaciones en las que se utilizan, su comportamiento, la forma en que se calcula el monto, el valor presente, así como su construcción,

Entradas relacionadas

• Ir a Matemáticas Financieras
• Entrada anterior
• Entrada siguiente

Introducción

Al momento se trabajó con el concepto general de anualidad, anualidad vencida, anticipada y diferida, así como algunas de sus combinaciones entre ellas, ejemplos de cómo se presentan en la vida cotidiana, y la forma en que resultan muy útiles, para poder encontrar una solución. Sin embargo, aún falta considerar el caso en el que los pagos pueden ser de forma ininterrumpida, por decirlo así: los pagos serían un tiempo «infinito», lo anterior, tiene efecto sobre el capital, el cual, bajo estas condiciones, provoca que nunca se acabe.

Definición del concepto de perpetuidad, descripción y valor presente

Éste concepto, se parece mucho a las anualidades, desde el punto de vista que consisten en una serie de pagos iguales, en los que, en teoría el tiempo tiende al infinito, esto es, la duración del plazo esta continua siempre, en otras palabras, no está definido el término del plazo, mientras la causa subsista, mientras alguna empresa continúe operando, dicha operación continuará existiendo. Un ejemplo de éste tipo de casos se da cuando quieren constituir un fondo, un premio como lo es el premio nobel, o podría ser el caso de los dividendos que otorgan las empresas cuya operación es indefinida, la asignación de becas, en todos esos casos la característica en las que coinciden es, que siempre haya recursos de los cuales disponer, para que nunca se quede en cero los fondos.

La forma en que será denotada una perpetuidad está dada por la expresión:

$$\prescript{}{\infty}{\mathbf{A}}_i.$$

Por otra parte, la notación usada para los conceptos de las anualidades anticipadas, vencidas, y diferidas será el mismo con el cual se han venido representando cada una respectivamente, sin embargo; para fines prácticos de éste concepto, será incluido el símbolo $\infty$ como subíndice, que como ya se mencionó hace corresponde al uso de una perpetuidad. En lo que respecta a las demás variables permanecerán con la misma denotación. Es importante hacer mención que el concepto de perpetuidad, se puede combinar con los conceptos que ya se han estado trabajando, y que se desarrollarán más adelante, recordemos algunos conceptos que serán utilizados para su construcción.

El valor presente de una anualidad vencida se calcula con la siguiente expresión:

$$\prescript{}{n}{\mathbf{A}}_i=\frac{1-v^n}{i}$$

nos vamos a enfocar en la parte derecha de la igual, específicamente al que contiene a la $n$, el cual corresponde al $v^n$, analizando lo que le ocurre cuando se hace tender a $n$ a infinito. Partiendo de que:

$$v^n=\frac{1}{(1+i)^n}.$$

Cuando $(1+i)^n$, si se hace tender $n$ a infinito, el comportamiento dicha expresión es de una progresión geométrica, por lo que el cociente que allí se expresa, al tener que el denominador se hace tender a infinito, entre algo pequeño, el resultado será cero. Esto hace transformar dicha expresión en:

$$\prescript{}{\infty}{\mathbf{A}}_i=\frac{1-v^{\infty}}{i}=\frac{1-0}{i}=\frac{1}{i}.$$

Ahora, si en vez de un peso, se cambia dicha cantidad por $X$, la expresión queda:

$$\prescript{}{\infty}{\mathbf{A}}_i=\frac{X}{i}$$

dicha ecuación representa el valor presente de una perpetuidad vencida.

De ésa ecuación que se acaba de obtener, se despeja $X$, se obtiene la expresión para calcular el capital inicial, la cual queda denotada por:

$$X=\prescript{}{\infty}{\mathbf{A}}_i i.$$

Monto

De acuerdo con las características que tiene el concepto de perpetuidad, el monto de éste tiende a ser infinito, ya que realizando el siguiente proceso se tiene:

$$\prescript{}{\infty}{\mathbf{S}}_{i}=\frac{(1+i)^{\infty}-1}{i}=\frac{\infty-1}{i}=\infty$$

esto ocurre toda vez que $(1+i)$ resulta ser siempre mayor que $1$, para cualquier $i$ positiva, además de que está elevada a una potencia $\infty$ lo que hace que el resultado sea infinito. Aunado a lo anterior está el hecho de que cualquier cifra infinita, dividida entre cualquier número, el resultado continúa siendo infinito.

Ejercicios resueltos

Ejercicio. Una fundación desea crear un fondo que cuente con recursos suficientes para solventar los gastos de 3 becas que serán asignadas a 3 estudiantes, de manera tal que cuando ellos terminen sus estudios, siga habiendo fondos, para seguir beneficiando a otros 3 estudiantes más. La beca consiste en una cantidad \$2,000 mensuales para cada uno. Se desea saber de ¿cuánto debe ser el capital que se requiere aportar para, si están considerando una cantidad de 8% efectiva anual?

Ejercicio. La familia Godínez, quiere generar un fondo de un millón de pesos, que garantice la educación de su hijo, si al día que se decide crearlo, tiene una edad de 20 años, necesita saber ¿cuánto debería ahorrar semanalmente para asegurar el dinero suficiente para que garantice los gastos cuando su hijo ingrese a la universidad, él señor Godínez calcula hacer dicho ahorro por unos 20 años. La tasa que se estará invirtiendo dichas aportaciones será del 8% efectiva anual.

Más adelante…

Se continuará estudiando las variantes de las anualidades que aún faltan por ver, como lo son las anualidades crecientes, éstas son utilizadas cuando las empresas, deciden ir incrementando el capital que se va abonando para liquidar una deuda, con la finalidad de pagar menos intereses, por ejemplo.

Entradas relacionadas

• Ir a Matemáticas Financieras
• Entrada anterior.
• Entrada siguiente.

Introducción

Éste tipo de anualidades, se presentan cuando las personas hacen la solicitud de un crédito, y éste considera un periodo de «gracia», el cual es un tiempo considerable que les otorgan por ejemplo mientras se hacen de una buena cartera de clientes, considerando el hecho de que, al ser una nueva empresa, no va a ser posible generar ingresos desde el día uno. Sin embargo, dicho periodo, sí está generando intereses, pero aun con eso, le permite a la persona que adquirió el crédito el no tener que estar pagando de forma inmediata dicha deuda.

Descripción y valor presente

Las anualidades diferidas son al tipo de anualidades en las que no se realizan los pagos desde el primer periodo, sino después de haber transcurrido el periodo de gracia que se haya pactado, el cual puede ser un período o más. Un ejemplo de éste tipo de créditos, son las promociones que sacan en el buen fin, «disfrute hoy de su pantalla, coche, o lo que sea que estén vendiendo y pague hasta enero del siguiente año».

De acuerdo a lo anterior, una anualidad diferida, es la que establece un plazo en el que no se va a realizar ningún pago, a dicho periodo se le conoce como diferimiento, y una vez transcurrido éste, se da inicio a la realización de los pagos de la forma conocida como una anualidad.

Una anualidad diferida es denotada por:

$$\prescript{}{m/n}{\mathbf{A}}_i=v_i^{m+1}+v_i^{m+2}+…+v_i^{m+n-2}+v_i^{m+n-1}+v_i^{m+n}$$

$$\prescript{}{m/n}{\mathbf{A}}_i=v_i^m(v_i^1+v_i^2+…+v_i^{n-2}+v_i^{n-1}+v_i^n)$$

$$\prescript{}{m/n}{\mathbf{A}}_i=v_i^m\prescript{}{n}{\mathbf{A}}_i$$

$$V=X\prescript{}{m/n}{\mathbf{A}}_i$$

$$V=X\prescript{}{m/n}{\mathbf{A}}_i=Xv_i^m\prescript{}{n}{\mathbf{A}}_i.$$

Reglas para su uso

• $m$ y $n$ son número enteros y se miden en la misma temporalidad, esto es, si n son semanas, m serán también semanas
• Los pagos se realizan de forma vencida, esto quiere decir que el primer pago se realizará al final del primer periodo que aparezca, una vez que haya concluido el periodo de gracia o periodo de diferimiento.
• La tasa de interés deberá ser efectiva por periodo, para los $n$ pagos, así como los $m$ periodos que conformen el periodo de diferimiento.

Monto

Para obtener el monto de una anualidad diferida, de forma semejante a las dos anualidades vistas anteriormente (anticipadas y vencidas), se continua tomando como referencia para su valuación, la fecha en la que realizo el último pago.

En la siguiente imagen, se muestra lo que se acaba de mencionar:

La expresión con la que se va a denotar una anualidad diferida es:

$$\prescript{}{n}{\mathbf{S}}_i=(1+i)^{n-1}+(1+i)^{n-2}+…+1$$

de donde se obtiene:

$$\prescript{}{n}{\mathbf{S}}_i=\frac{(1+i)^n-1}{i}.$$

De forma análoga a las anteriores anualidades, ésta expresión denota los pagos con valor de \$1.00, para hacerlo de forma más general se considera pagos de cantidad $X, y la expresión queda:

$$M=X\prescript{}{n}{\mathbf{S}}_i=X\frac{(1+i)^n-1}{i}.$$

En este momento, ya se tienen 3 tipos de anualidades, por lo que ya se cuenta con el material necesario para resolver problemas que involucran combinaciones entre ellas.

Ejercicios resueltos

Ejercicio. Una persona necesita un crédito por \$80,000 para reparar su vehículo, ya que es modelo antiguo y lo quiere volver un coche clásico. El banco decide otorgarle el crédito, y además le otorga un periodo de gracia por 4 meses, comenzando a pagar a partir del final del quinto mes. La deuda debe ser pagada en 24 mensualidades. Se desea saber la cantidad que tendrán dichas mensualidades, con una tasa del 1.5% efectivo mensual.

Ejercicio. Supongamos que una persona contrata un crédito por \$100,000 y lo quiere liquidar en 10 mensualidades vencidas con pagos de \$4000, posteriormente realizará pagos durante 8 mensualidades iguales, que serán pagadas luego de un periodo de gracia de 6 meses. Se necesita saber ¿Cuánto es el monto de las 8 mensualidades, a una tasa de interés del 1.3% mensual?

Más adelante…

En las siguientes secciones se continuará otros tipos de anualidades, su combinación entre ellas, la forma en que se aplican para la resolución de problemas.

Entradas relacionadas

• Ir a Matemáticas Financieras
• Entrada anterior
• Entrada siguiente