Introducción
En esta sección veremos curvas que se pueden representar por un sistema de ecuaciones llamadas ecuaciones paramétricas, ya que formalmente estas curvas no son funciones, es decir, no cumplen el criterio de la definición de función $(y=f(x))$, por lo que solo le llamamos curvas, denotado comúnmente por la letra $C$ a estas curvas.
Curvas paramétricas
Sea $C$ una curva en el plano como en la figura $(1)$, las coordenadas de $x$ y $y$ son funciones de otra variable, generalmente denotada por la variable $t$, por tanto, podemos escribir:
$$x=f(t) \space \space \space \space y \space \space \space \space y=g(t)$$
A la variable $t$ se le conoce como parámetro, y a las ecuaciones anteriores se le conocen como las ecuaciones paramétricas de la curva $C$. Notemos que cada valor de $t$ determina un punto $(x, y)$ por lo que cuando $t$ va variando, el punto $(x,y)=(f(t), g(t))$ también va variando trazando la curva $C$.
Veamos un ejemplo.
Ejemplo
- Grafica la curva definida por la siguientes ecuaciones paramétricas: $x=t^{2}-2t \space \space \space y=t+1$.
Para graficar este tipo de curvas tenemos que ir variando la variable $t$, por lo que obtenemos algunos valoras bajo las curvas paramétricas en la tabla siguiente:
| t | x | y |
| -2 | 8 | -1 |
| -1 | 3 | 0 |
| 0 | 0 | 1 |
| 1 | -1 | 2 |
| 2 | 0 | 3 |
| 3 | 3 | 4 |
| 4 | 8 | 5 |
De los valores anteriores obtenemos la curva siguiente:
De la ecuación para $y$ tenemos que:
$$t=y+1$$
Si sustituimos esta ecuación en la ecuación para $x$ entonces tenemos que:
$$x=t^{2}-2t=(y+1)^{2}-2(y+1)=y^{2}-4y+3$$
Por tanto, la curva representada por las ecuaciones paramétricas es una parábola.
- Que curva representa las siguientes ecuaciones paramétricas: $x=\cos(t)$ y $y=\sin(t)$ con $0\leq t \leq 2\pi$
Podemos eliminar la variable $t$ elevando al cuadrado las variables $x$ y $y$, sumando estos términos obtenemos:
$$x^{2}+y^{2}=\cos^{2}(t)+\sin^{2}(t)=1$$
Por tanto, notamos que es la ecuación de una circunferencia de radio $1$ como vemos en la siguiente figura $(3)$.
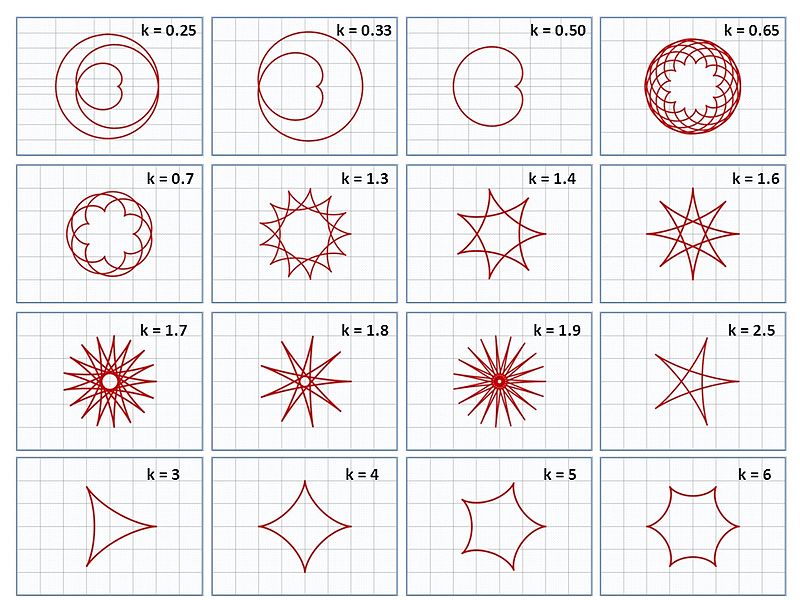
En algunos casos algunas curvas paramétricas forman algunas figuras espectaculares, por ejemplo, el hipocicloide definido como:
$$x=(a-b)\cos(t)+\cos(t \left ( \frac{a}{b} \right )-1)$$
$$y=(a-b)\sin(t)-\sin(t \left ( \frac{a}{b} \right )-1)$$
Donde el radio del círculo más grande es $a$ y el radio del círculo más pequeño es $b$, sea $k=\frac{a}{b}$ donde a $k$ se le conoce como el número de cúspides, por lo que al variar estos valores obtenemos las curvas siguientes:
Tarea moral
Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invito a resolver los siguientes ejercicios propuestos relacionados con el tema visto.
Grafique las siguientes curvas paramétricas en el intervalo indicado.
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- $x=\sin(2t) \space \space y=\cos(2t), \space \space \space 0 \leq t \leq 2\pi$
- $x=2\sin(t) \space \space y=4+\cos(t), \space \space \space 0 \leq t \leq 3\pi/2$
- $x=t \space \space y=t^{2}, \space \space \space -2 \leq t \leq 2$
- Elimine el parámetro para hallar la ecuación cartesiana de la curva dada como: $$x=t^{2}-2 \space \space y=5-2t, \space \space \space -3 \leq t \leq 4$$
- Encuentre las ecuaciones paramétricas de una circunferencia de radio $r$ y centro $(h, k)$.
Más adelante…
En esta sección vimos curvas paramétricas y como graficarlas, en la siguiente sección veremos como calcular la tangente de una curva paramétrica.
Entradas relacionadas
- Ir a Cálculo Diferencial e Integral II.
- Entrada anterior del curso: Cálculo Diferencial e Integral II: Forma exponencial de las series de Fourier – El blog de Leo (nekomath.com)
- Siguiente entrada del curso: Cálculo Diferencial e Integral II: Tangentes a curvas paramétricas – El blog de Leo (nekomath.com)

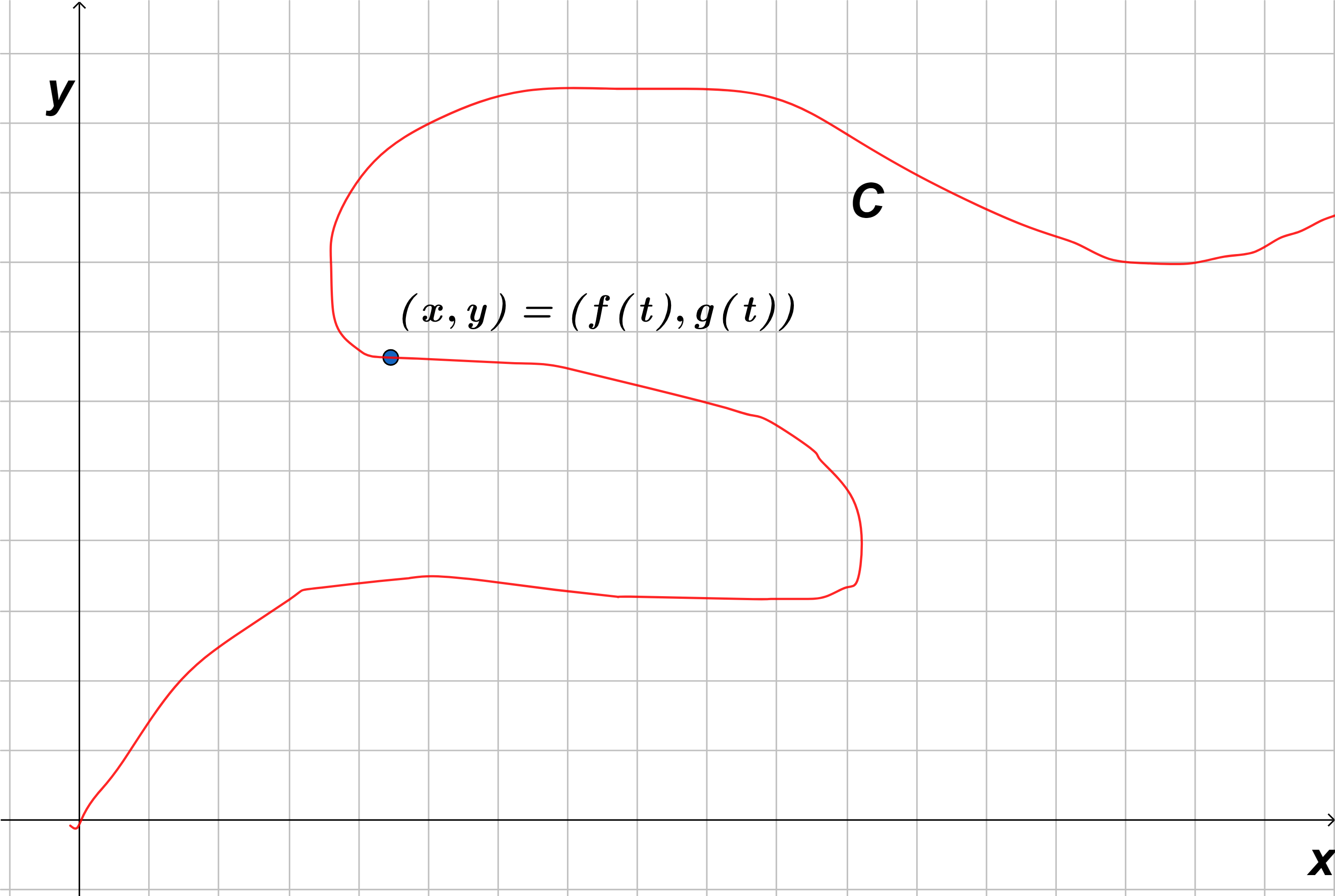
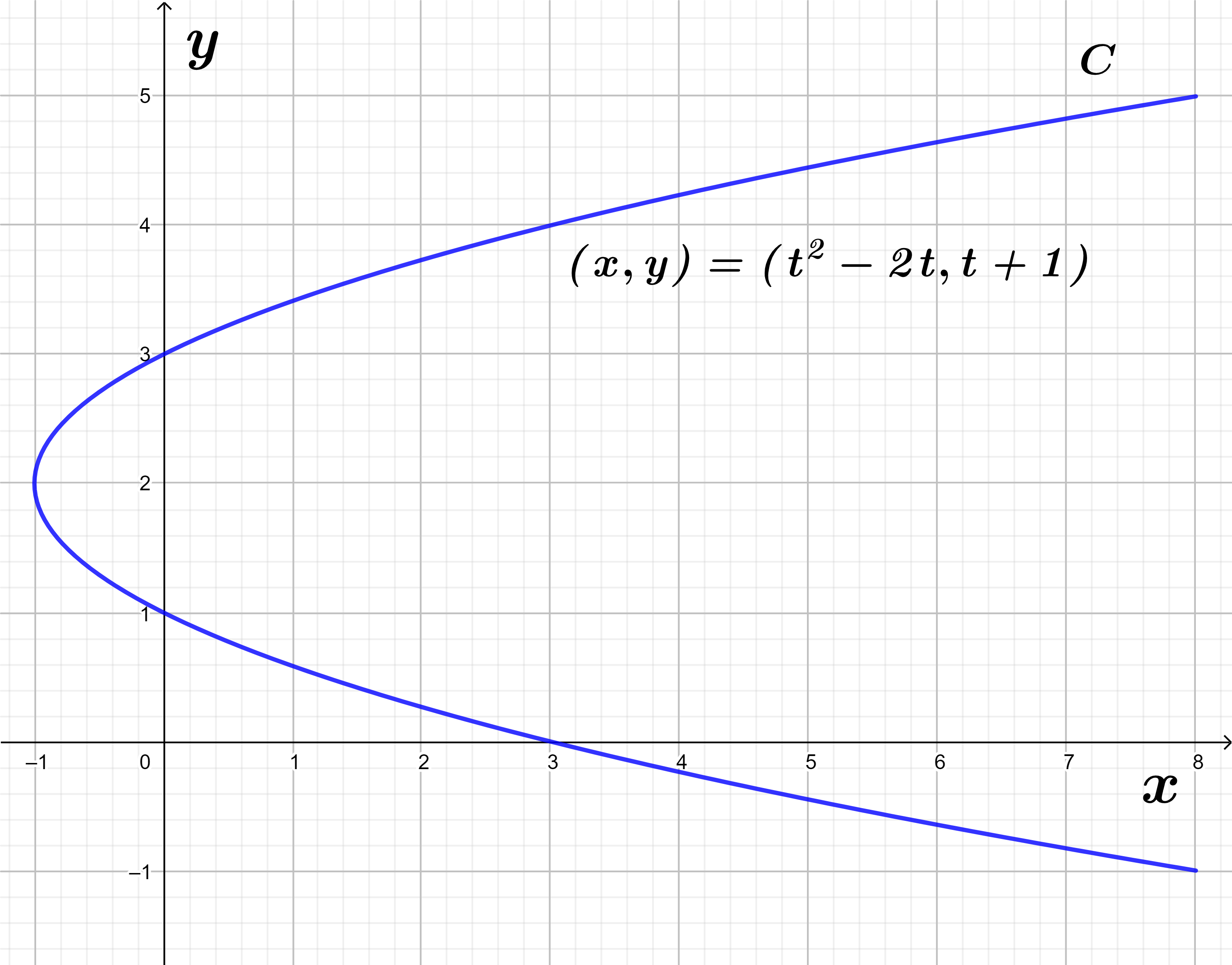
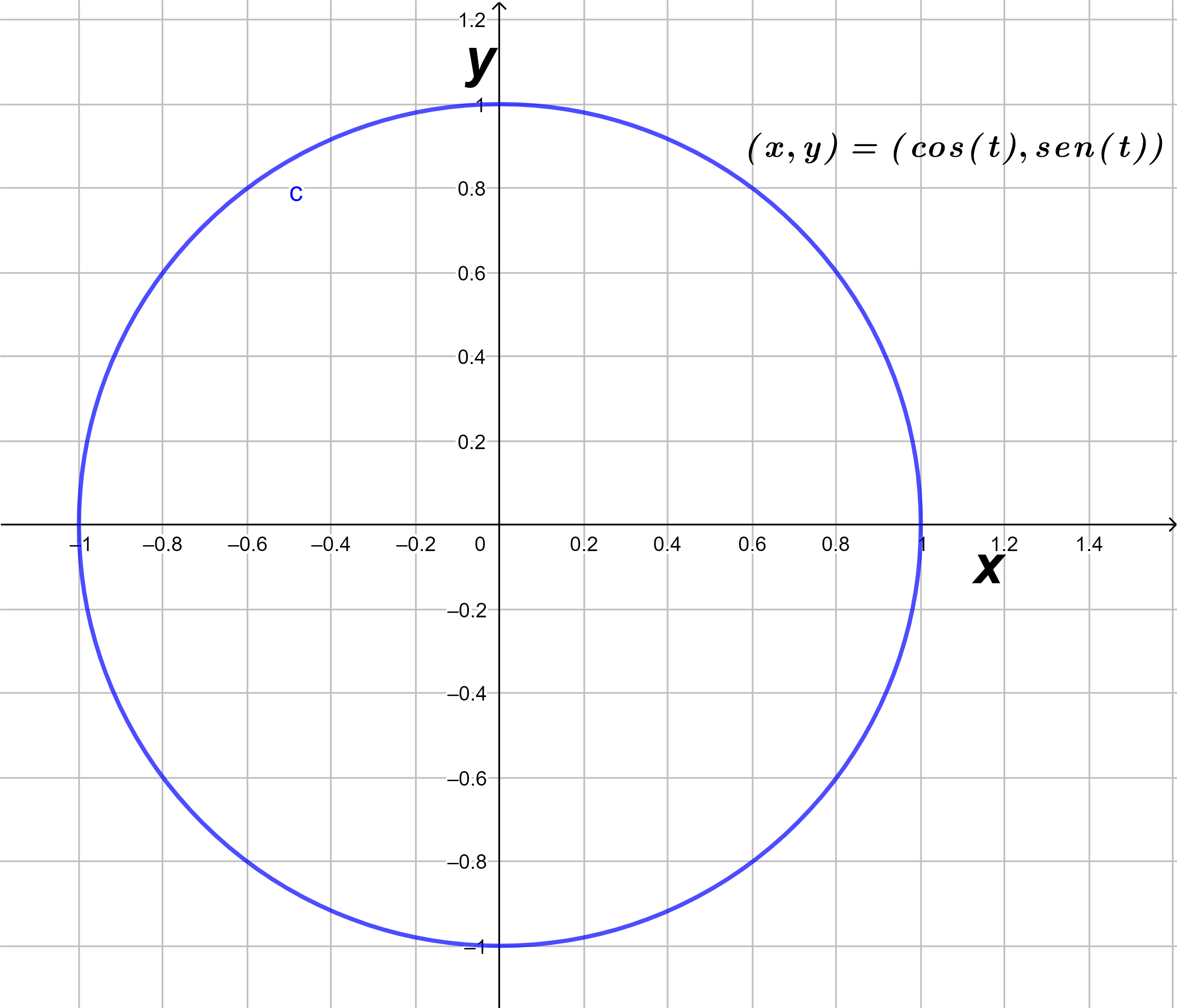
En el ejemplo hay un error de dedo y = t + 1 debiendo ser y = t – 1
Hola, en efecto, hay un error de dedo en el ejemplo pero el error esta en la imagen el cual se tenia y=t-1 cuando debe ser y=t+1.
Muchas gracias por notificarnos, ya esta solucionado.