Introducción
Después de haber revisado algunos ejemplos de límite de funciones, estamos listos para conocer y demostrar algunas de las propiedades; para este fin, usaremos la relación existente entre el límite de una función y el de una sucesión demostrada en la entrada anterior.
Teoremas sobre el límite de una función
Considerando el criterio de sucesiones para límites visto anteriormente, es natural que haya una gran cantidad de propiedades que se hereden del límite de sucesiones. A continuación revisaremos algunas de ellas y podremos aprovechar la relación de ambos conceptos para hacer la demostración de las mismas.
Teorema. Sean $f: A \rightarrow \mathbb{R}$ y $g: A \rightarrow \mathbb{R}$ dos funciones y sea $c \in \mathbb{R}$. Si $$\lim_{x \to x_0} f(x) = L \quad \text{ y } \quad \lim_{x \to x_0} g(x) = M.$$
Entonces
- $$\lim_{x \to x_0} c \cdot f(x) = cL.$$
- $$\lim_{x \to x_0} (f+g)(x) = L+M.$$
- $$\lim_{x \to x_0} (f-g)(x) = L-M.$$
- $$\lim_{x \to x_0} (f \cdot g)(x) = L\cdot M.$$
- Si además $M \neq 0$, entonces $$\lim_{x \to x_0} \left( \frac{f}{g} \right) (x) = \frac{L}{M}.$$
Demostración
Daremos la demostración del inciso 4 y la demostración de los demás es análoga.
Sea $\{ a_n \}$ una sucesión en $A$ que converge a $x_0$ tal que $a_n \neq x_0$ para todo $n\in \mathbb{N}$, por el teorema anterior tenemos que
$$\lim_{n \to \infty} f(a_n) = L \quad \text{ y } \quad \lim_{n \to \infty} g(a_n) = M.$$
De esta forma podemos usar las propiedades de convergencia de una sucesión, así
$$\lim_{n \to \infty} (f \cdot g)(a_n) = \lim_{n \to \infty} \left( f(a_n) \cdot g(a_n) \right) = \lim_{n \to \infty} f(a_n) \cdot \lim_{n \to \infty} g(a_n) = L \cdot M.$$
Por el teorema revisado, podemos concluir que $$\lim_{x \to x_0} (f \cdot g)(x) = L \cdot M.$$
$\square$
Observación. Particularmente podemos generalizar los puntos 2 y 4, de tal forma que si $f_1, f_2, \dots, f_n$ son funciones definidas de $A$ a $\mathbb{R}$ cada una con límite $L_1, L_2, \dots L_n$ en $x_0$. Entonces
\begin{gather*}
\lim_{x \to x_0} (f_1 + f_2 + \ldots + f_n) (x) = L_1 + L_2 + \ldots + L_n \\
\text{ y } \\
\lim_{x \to x_0} (f_1 \cdot f_2 \cdot \ldots \cdot f_n)(x) = L_1 \cdot L_2 \cdot \ldots \cdot L_n.
\end{gather*}
Revisaremos un par de ejemplos donde aplicaremos las propiedades anteriores.
Ejemplo 1. Calcula $$\lim_{x \to 2} \frac{5x-12}{2x + 10}.$$
\begin{align*}
\lim_{x \to 2} \frac{5x-12}{2x + 10} =& \frac{ \lim_\limits{x \to 2} ( 5x-12 ) }{ \lim_\limits{x \to 2} (2x + 10) } \text{, por el punto 5 del teorema anterior} \\ \\
= & \frac{ \lim_\limits{x \to 2} 5x – \lim_\limits{x \to 2} 12 }{ \lim_\limits{x \to 2} 2x + \lim_\limits{x \to 2} 10 } \text{, por los puntos 2 y 3 del teorema anterior} \\ \\
= & \frac{10-12}{4+10} \\ \\
= & – \frac{1}{7}.
\end{align*}
$$\therefore \lim_{x \to 2} \frac{5x-12}{2x + 10} = – \frac{1}{7}.$$
Ejemplo 2. Calcula $$\lim_{x \to 5} \frac{x^3+3}{8x^2 + 7}.$$
\begin{align*}
\lim_{x \to 5} \frac{x^3+3}{8x^2 + 7} = & \frac{\lim_\limits{x \to 5} (x^3+3)}{ \lim_\limits{x \to 5} (8x^2 + 7)} \text{, por el punto 5 del teorema anterior} \\ \\
= & \frac{\lim_\limits{x \to 5} x^3+ \lim_\limits{x \to 5} 3}{ \lim_\limits{x \to 5} 8x^2 + \lim_\limits{x \to 5} 7} \text{, por el punto 2 del teorema anterior} \\ \\
= & \frac{125+ 3}{200 + 7} \\ \\
= & \frac{128}{207}.
\end{align*}
$$\therefore \lim_{x \to 5} \frac{x^3+3}{8x^2 + 7} = \frac{128}{207}.$$
En los ejemplos anteriores se hizo énfasis en las propiedades que nos permitieron calcular el límite con la finalidad de mostrar claramente cómo se emplean, sin embargo, esto no será necesario y, de hecho, no se hará tal hincapié de ahora en adelante.
A continuación probaremos el teorema del sándwich para el límite de una función.
Teorema. Sean $f$, $g$, $h : A \rightarrow \mathbb{R}$ y sea $x_0 \in A$. Si
$$f(x) \leq g(x) \leq h(x) \text{, para todo } x \in A, x \neq x_0,$$
y si $$\lim_{x \to x_0} f(x) = L \quad \text{ y } \quad \lim_{x \to x_0} h(x) = L.$$
Entonces
$$\lim_{x \to x_0} g(x) = L.$$
Demostración
Sea $\varepsilon > 0 $, como $f$ y $h$ tienen como límite a $L$ en $x_0$, entonces existen $\delta_1$, $\delta_2$ tales que
\begin{gather*}
0<|x-x_0|< \delta_1, \quad \text{entonces} \quad |f(x)-L|< \varepsilon \\
\text{ y } \\
0<|x-x_0|< \delta_2, \quad \text{entonces} \quad |h(x)-L| < \varepsilon.
\end{gather*}
Consideremos $\delta = min\{ \delta_1, \delta_2 \}$, si $0<|x-x_0|< \delta$, se cumple que
\begin{gather*}
-\varepsilon < f(x)-L < \varepsilon \quad \Leftrightarrow \quad L-\varepsilon < f(x) < L + \varepsilon \\
\text{ y } \\
-\varepsilon < h(x)-L < \varepsilon \quad \Leftrightarrow \quad L-\varepsilon < h(x) < L + \varepsilon.
\end{gather*}
Además, por hipótesis se tiene que $f(x) \leq g(x) \leq h(x)$, entonces
\begin{gather*}
L-\varepsilon < f(x) \leq g(x) \quad \text{ y } \quad g(x) \leq h(x) < L + \varepsilon.
\end{gather*}
Se sigue que
\begin{gather*}
L-\varepsilon < g(x) < L + \varepsilon. \\ \\
\Leftrightarrow -\varepsilon < g(x) – L< \varepsilon. \\ \\
\therefore |g(x) – L| < \varepsilon. \\ \\
\therefore \lim_{x \to x_0} g(x) = L.
\end{gather*}
$\square$
A continuación veremos un ejemplo donde podemos aplicar el teorema del sándwich.
Ejemplo 3. Encuentra el siguiente límite: $$\lim_{x_0 \to 0} x^2 e^{sen(\frac{1}{x})}.$$
Sabemos que
\begin{gather*}
– 1 \leq sen(\frac{1}{x}) \leq 1 \text{, para todo } x \neq 0.
\end{gather*}
Dado que la función exponencial no altera la relación de orden, entonces tenemos
\begin{gather*}
e^{- 1} \leq e^{sen(\frac{1}{x})} \leq e^{ 1}.
\end{gather*}
Se sigue que
\begin{gather*}
x^2 e^{- 1} \leq x^2 e^{sen(\frac{1}{x})} \leq x^2 e^{ 1}.
\end{gather*}
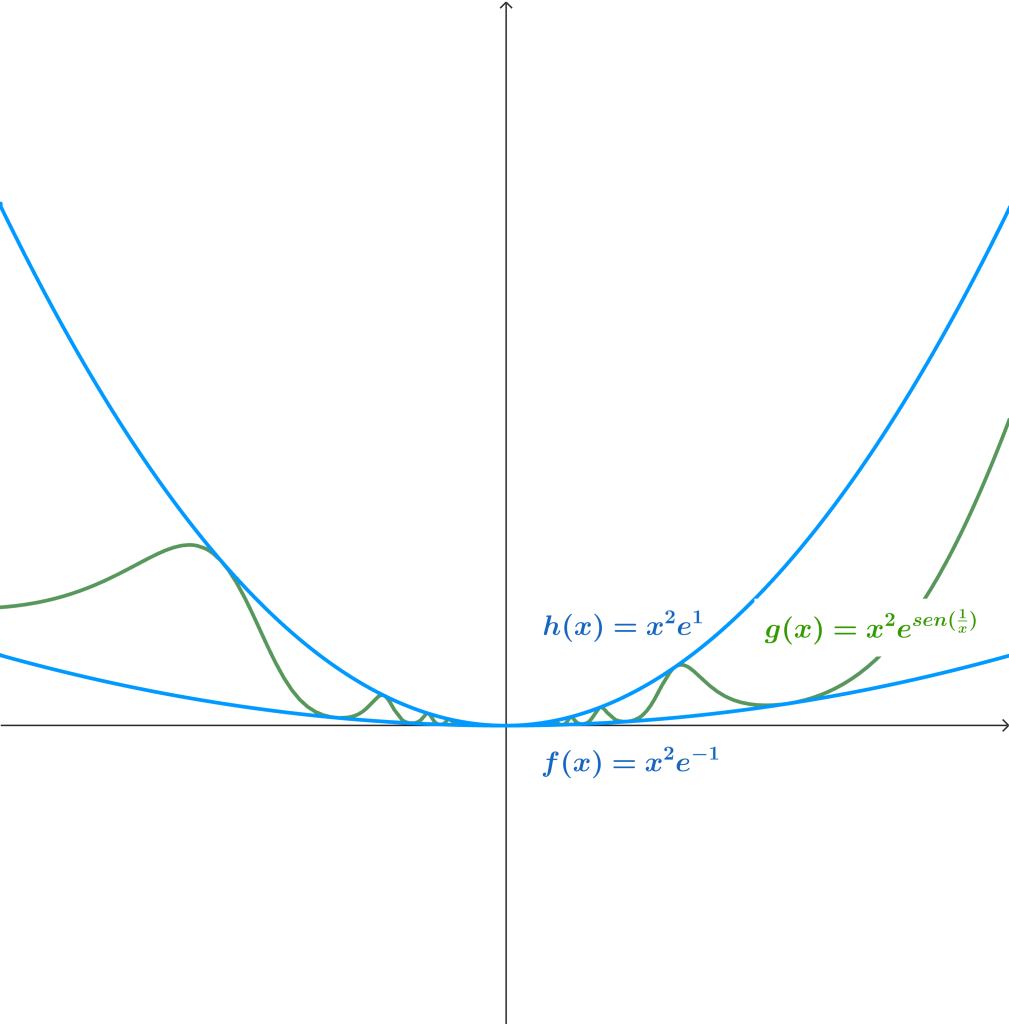
La función original $g(x) = x^2 e^{sen(\frac{1}{x})}$ está acotada por $f(x) = x^2 e^{- 1}$ y $h(x) = x^2 e^{1}$. Tal como se muestra en la siguiente gráfica:
Notemos que
$$\lim_{x \to 0} x^2 e^{- 1} = 0 \quad \text{ y } \quad \lim_{x \to 0} x^2 e^{1} = 0.$$
Por el teorema del sándwich podemos concluir que $$\lim_{x_0 \to 0} x^2 e^{sen(\frac{1}{x})} = 0.$$
En esta entrada revisamos algunas de las propiedades que tiene el límite de una función haciendo uso del límite de sucesiones, pero vale la pena destacar que también se pudo recorrer este tramo del camino usando la definición épsilon-delta y te invitamos a realizar el ejercicio de demostrar algunas de las propiedades haciendo uso de tal definición con la finalidad de tener un dominio mayor del concepto.
Más adelante…
Extenderemos la noción de límite de una función definiendo una nueva clase de límites: los límites laterales. Veremos la definición de límite por la derecha y límite por la izquierda que son definiciones menos exigentes y las cuales nos permiten tener un análisis más detallado para aquellas funciones donde el límite no existe.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Prueba que si $$\lim_{x \to x_0} f(x) = L \text{, entonces } \lim_{x \to x_0} |f(x)| = |L|.$$
- Calcula el límite $$\lim_{x \to 0} \frac{(x+1)^2-1}{x}.$$
- Calcula el límite $$\lim_{x \to 0} \frac{\sqrt{x}-1}{x-1}.$$
- Calcula el límite $$\lim_{x \to 0} x^2 cos \left( \frac{1}{x^2} \right).$$
Entradas relacionadas
- Ir a Cálculo Diferencial e Integral I
- Entrada anterior del curso: Límite de una función a través de sucesiones
- Siguiente entrada del curso: Límites laterales
- Resto de cursos: Cursos
Agradecimientos
Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»