Introducción

Recordemos que la derivada de una función $f$ se puede escribir del siguiente modo:
$$f'(x)=\dfrac{df(x)}{dx}.$$

Si nosotros tenemos una cantidad $x$ que se encuentra en función del tiempo $t$, haciendo uso de la derivada podemos expresar a la razón de cambio de $x$ respecto de $t$ como:
$$\dfrac{dx}{dt}.$$
De este modo, si se tiene que dicha cantidad $x$ está relacionada con una ecuación, para obtener su razón de cambio bastaría con derivarla.

Esta interpretación de la derivada nos será de utilidad para resolver los problemas que revisaremos a continuación.

Problema 1

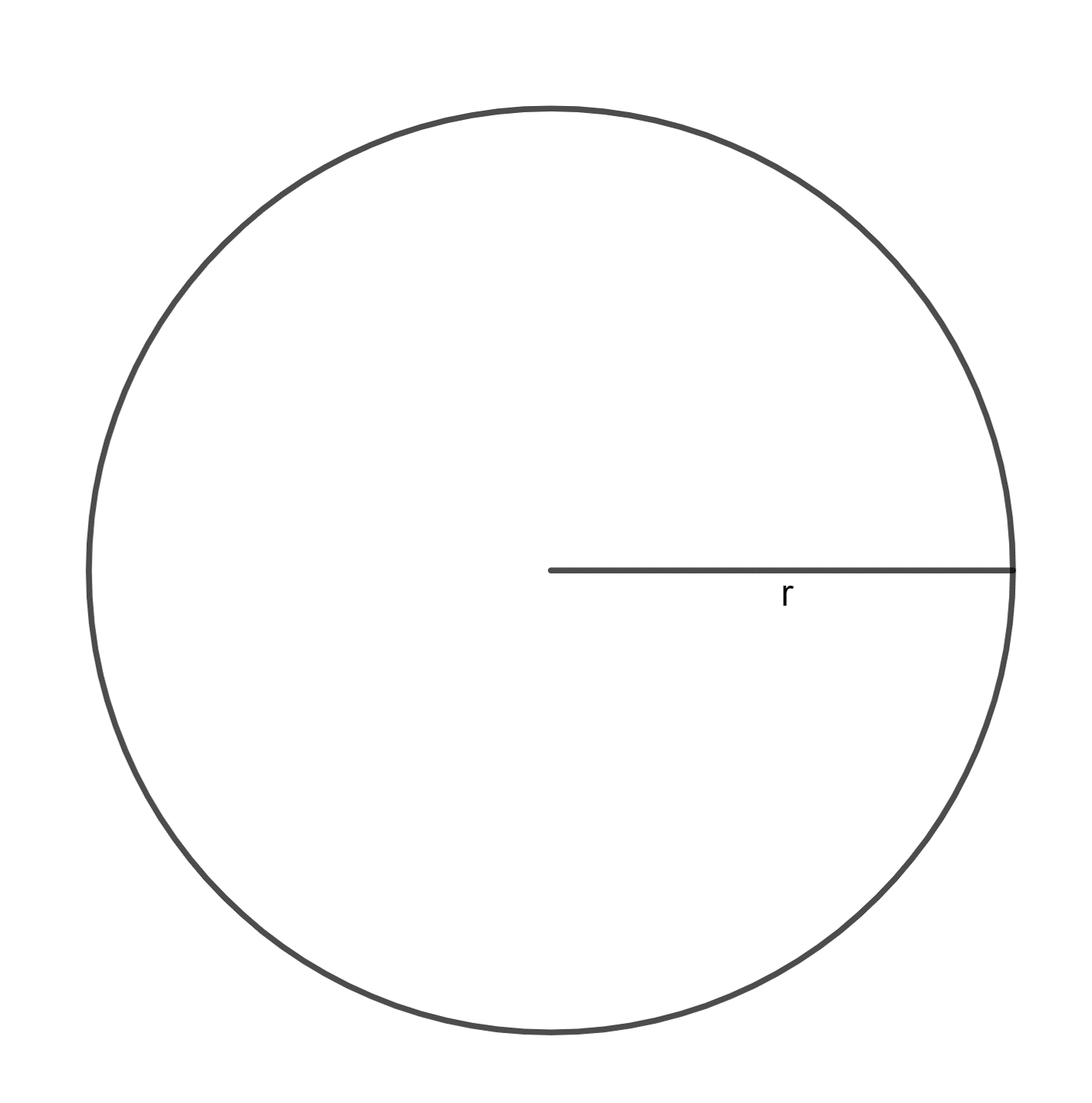
Un círculo expande su área de manera no especificada. Se sabe que cuando el radio es de $6 cm$, la tasa de variación del mismo respecto al tiempo es de $4 cm$.

Encuentra la tasa de variación del área respecto al tiempo cuando el radio $6 cm$.
Solución:
Sabemos que el área de un círculo está dada por:
$$A=\pi r^{2}.$$
Veamos que la tasa de variación del radio $r$ es:
$$\dfrac{dr}{dt}.$$

Al derivar el área $A$ respecto del tiempo $t$ tenemos:
$$\dfrac{dA}{dt}=2\pi r \dfrac{dr}{dt}$$
$(1)$

De los datos que nos dan en el problema sabemos que cuando el radio es de $6 cm$, su tasa de variación:
$$\dfrac{dr}{dt}=4 cm.$$

Sustituyendo estos valores en $(1)$ tenemos:
\begin{align*}
\dfrac{dA}{dt}&= 2\pi (6 cm)(4 cm)\\
&=48 \pi cm^{2}
\end{align*}

Por lo que la tasa de variación buscada es:
$$\dfrac{dA}{dt}= 48 \pi cm^{2}.$$

Problema 2

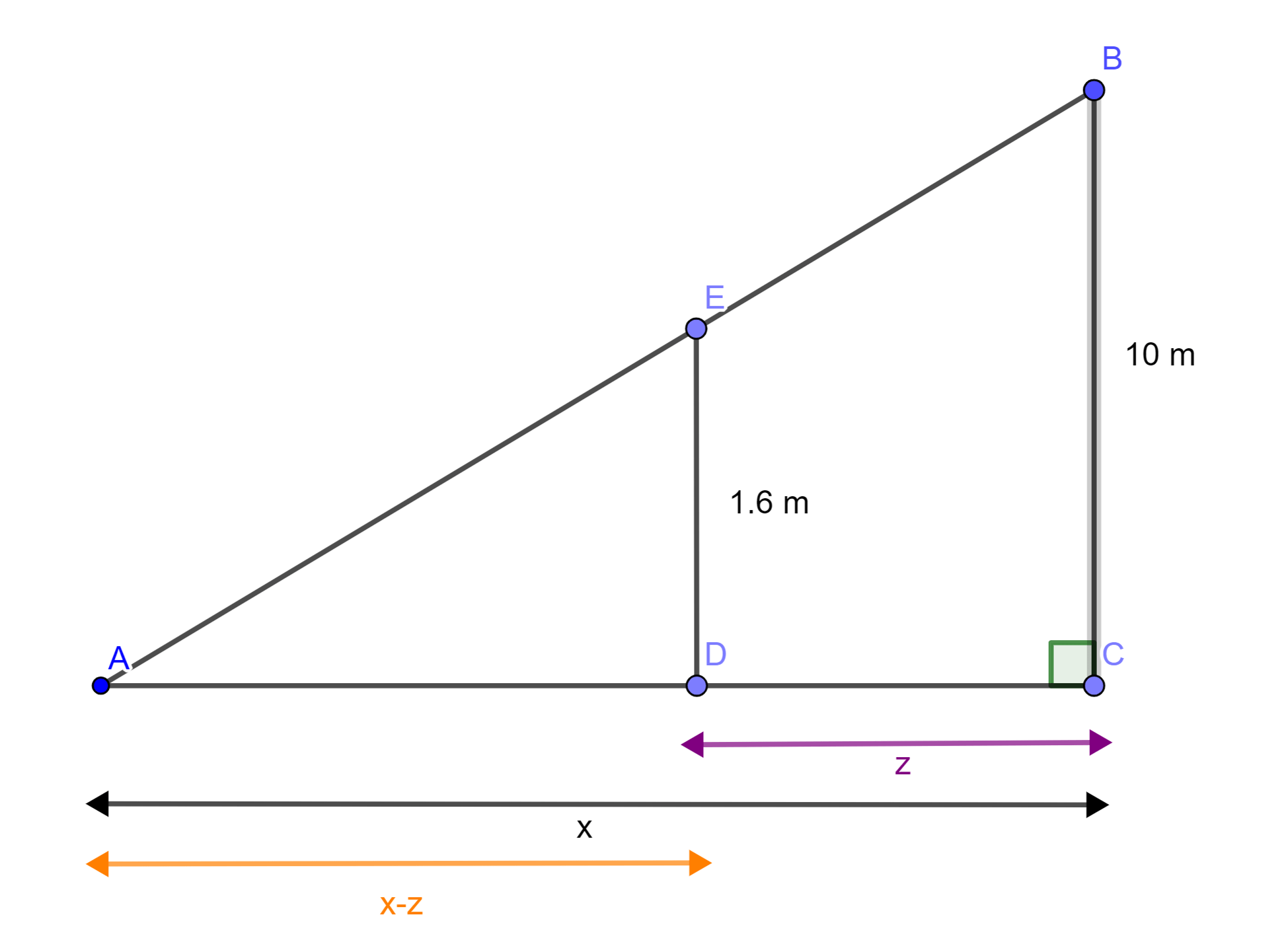
Por la mañana, una mujer se encuentra esperando a lado de un poste el autobús que la llevará a su trabajo. Debido a la demora, ella decide caminar rumbo al metro alejándose del poste que sabemos alumbra a razón de $3\frac{m}{s}$. Si además sabemos que la estatura de la mujer es de $1.60 m$ y la altura del poste de $10 m$, ¿cuál es la razón de cambio a la cual se mueve el extremo de la sombra de la mujer?

Solución:

Vemos que el problema nos dice que:
$$\dfrac{dz}{dt}=3 \frac{m}{s}.$$
Y que queremos obtener la razón de cambio:
$$\dfrac{dx}{dt}.$$
Observamos que los siguientes triángulos son semejantes:
$$\triangle ABC \sim \triangle AED.$$
Entonces tenemos la siguiente igualdad:
$$\frac{10}{1.6}=\frac{x}{x-z}.$$
Desarrollando lo anterior:
\begin{align*}
10(x-z)=1.6x &\Leftrightarrow 10x-10z=1.6x\\
&\Leftrightarrow 10x-1.6x=10z\\
&\Leftrightarrow 8.4x=10z
\end{align*}

Derivando con respecto del tiempo $t$:
$$8.4\dfrac{dx}{dt}=10\dfrac{dz}{dt}.$$

Despejando $\dfrac{dx}{dt}$:
$$\dfrac{dx}{dt}=\frac{10}{8.4}\dfrac{dz}{dt}.$$

Sustituyendo el valor conocido de $\dfrac{dz}{dt}$:
\begin{align*}
\dfrac{dx}{dt}&=\frac{25}{21}(3)\\
&=\frac{25}{7} \frac{m}{s}
\end{align*}

Por lo tanto, la razón con que se mueve el extremo de la sombra es de:
$$ \frac{25}{7} \frac{m}{s}.$$

Problema 3

Una pelota esférica se infla a razón de $0.16 \frac{cm^{3}}{min}$. ¿Cuál es su volumen cuando su radio está aumentando a razón de $0.20 \frac{cm}{min}$?

Solución:
Recordemos que el volumen de una esfera esta dado por:
$$V=\frac{4}{3}\pi r^{3}.$$
De los datos del problema sabemos lo siguiente:
\begin{align*}
\dfrac{dV}{dt}&= 0.16\frac{cm^{3}}{min} & \dfrac{dr}{dt}&=0.20\frac{cm}{min}
\end{align*}

Derivamos el volumen $V$ respecto del tiempo y obtenemos:
$$\dfrac{dV}{dt}=4\pi r^{2} \dfrac{dr}{dt}.$$

Sustituyendo $ \dfrac{dV}{dt}= 0.16$ en la igualdad anterior:
$$0.16 \frac{cm^{3}}{min} =4\pi r^{2} \dfrac{dr}{dt}.$$

Ahora sustituyendo el valor de la razón de cambio del radio:
$$0.16 \frac{cm^{3}}{min} =4\pi r^{2} \left(0.2 \frac{cm}{min} \right).$$

Para poder obtener el valor del volumen solicitado debemos conocer el valor del radio, por lo que despejando $r$ ocurre lo siguiente:
\begin{align*}
\frac{0.16}{0.8}\frac{cm^{2}}{\pi}&=r^{2}\\
\Rightarrow \frac{cm^{2}}{5\pi}&=r^{2}
\end{align*}
$$\therefore r=\frac{1}{\sqrt{5\pi}}cm.$$

Sustituyendo el valor de $r$ en el volumen tenemos que:
\begin{align*}
V&=\frac{4}{3}\pi \left( \frac{1}{\sqrt{5\pi}}\right)^{3}cm^{3}\\
&\approx 0.06728 cm^{3}
\end{align*}
Concluimos que el volumen aproximado de la pelota es de $ 0.06728 cm^{3}$.

Más adelante

En la próxima entrada revisaremos el tema de polinomios de Taylor. Para ello, veremos su definición formal y algunos ejemplos de su aplicación para aproximar valores de una función.

Tarea moral

• En una fábrica de hielo se tiene un cubo con volumen $V=5 m^{3}$. Por falta de espacio, los trabajadores deben sacarlo del congelador, provocando que comience a derretirse a razón de $2 \frac{m^{3}}{s}$, ellos se preguntan: ¿Cuál es la razón de cambio de la superficie del cubo en ese preciso instante?
• Un tronco de madera cuyo largo es de $13 m$ se encuentra apoyado sobre un muro. Se te pide hallar la velocidad con la que baja el extremo superior del tronco cuando su extremo inferior dista del muro $5m$. Se sabe que el tronco se separa a razón de $5 \frac{m}{s}$
• Un barco pesquero de $6 m$ de altura se aleja de un faro cuya altura es de $130 m$ y alumbra con una razón de $40 \frac{m}{s}$. Determina la razón de cambio a la cual se mueve el extremo de la sombra del barco.

Entradas relacionadas

• Ir a: Cálculo Diferencial e Integral I
• Entrada anterior del curso: Cálculo Diferencial e Integral I: Velocidad y aceleración.
• Entrada siguiente del curso: Cálculo Diferencial e Integral I: Polinomios de Taylor (Parte 1).
• Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»