Introducción

En cursos de Cálculo en el bachillerato, posiblemente resolviste ejercicios en los cuales te solicitaban hallar los puntos críticos de una función y realizar la gráfica de la misma basándote en ellos.
Recordemos primero que un punto crítico $x$ de una función $f$ es aquel que al evaluarlo en la derivada de $f$ nos da la siguiente igualdad:
$$f^{\prime }(x)=0.$$

Y que en el conjunto de estos puntos críticos se encontraban los máximos y mínimos de la función $f$.
En esta entrada daremos las definiciones formales correspondientes y veremos los Criterios de las derivadas para identificarlos. También veremos resultados en los que, haciendo uso de la derivada, podremos determinar si una función es creciente o decreciente en un intervalo.

Máximo y mínimo global

Definición: Sea $f:D_f\subseteq \mathbb{R}\to \mathbb{R}$ una función y $x_0\in D_f$. Decimos que en $x_0$ se alcanza:

• Un máximo global si para toda $x\in D_f$ se cumple que:
  $$f(x)\le f(x_0).$$
• Un mínimo global si para toda $x\in D_f$ se cumple que:
  $$f(x_0)\le f(x).$$

Máximo y mínimo local

Definición: Consideremos a una función $f$ continua en un intervalo $I$ y $x_0\in (x_0-r,x_0+r)\subseteq I$ con $r\in {\mathbb{R}}^{+}$ y tenemos que existe $f(x_0)$ decimos que:

• $x_0$ es un máximo local de $f\iff$ existe $r>0$ tal que para todo $x\in (x_0-r,x_0+r)\subseteq D_f$ ocurre que:
  $$f(x)\le f(x_0).$$
• $x_0$ es un mínimo local de $f\iff$ existe $r>0$ tal que para todo $x\in (x_0-r,x_0+r)\subseteq D_f$ ocurre que:
  $$f(x_0)\le f(x).$$
• $x_0$ no es máximo ni mínimo si existen $x_1,x_2$ tales que para toda $r>0$ y para cualquier $x\in (x_0-r,x_0+r)$ ocurre que:
  $$f(x_1)<f(x_0)<f(x_2).$$

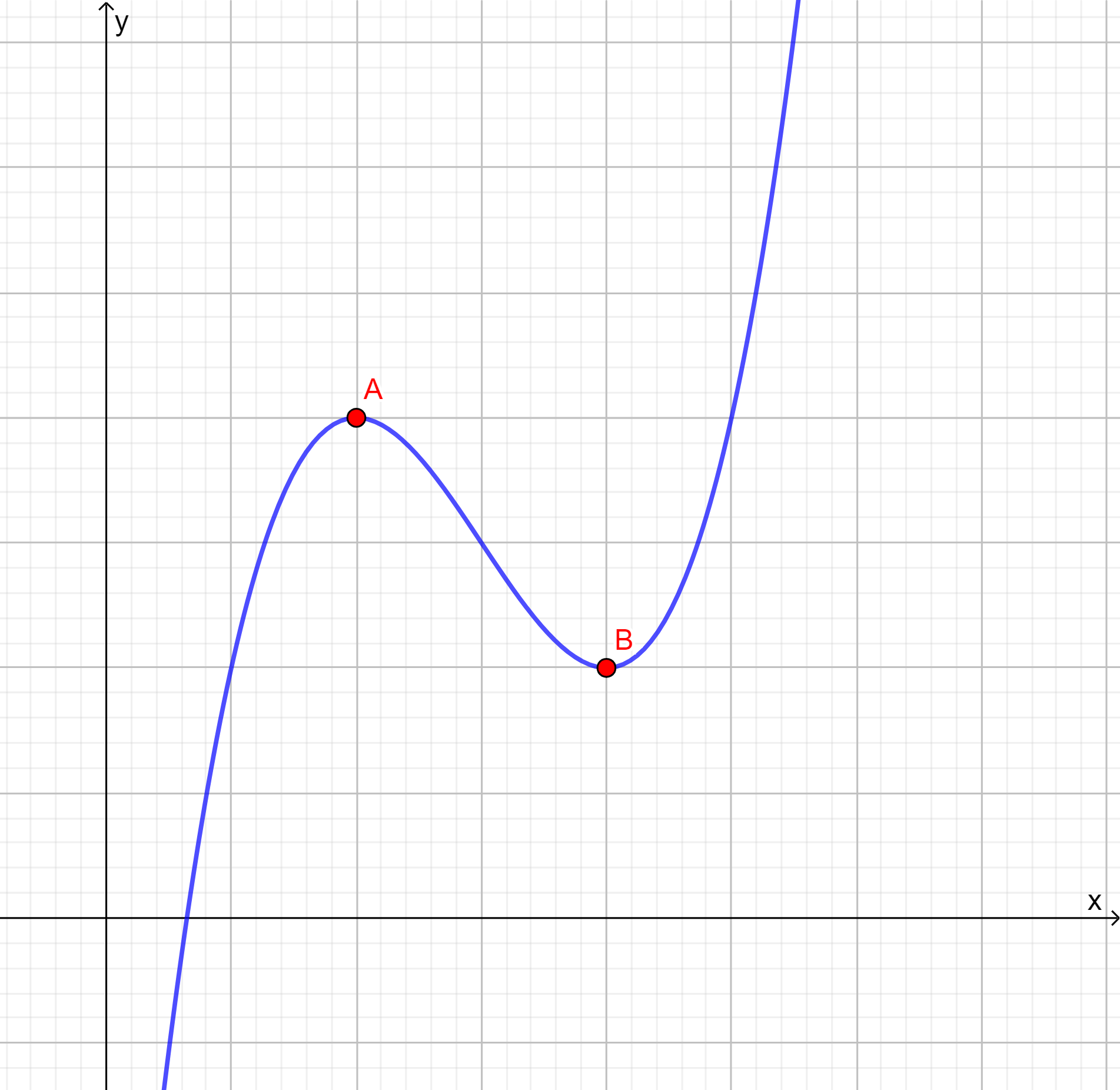
En la imagen anterior vemos que el punto $A$ es un máximo de la función y $B$ un mínimo.

La derivada y los puntos críticos

Teorema: Consideremos una función $f$ continua en un intervalo $I$ y es derivable en el punto $x_0\in (x_0-r,x_0+r)\subseteq I$.

Si tenemos que $x_0$ es un máximo o un mínimo local de $f\Rightarrow f^{\prime }(x_0)=0$.

Demostración: Tomemos $x_0$ máximo local de $f$, así por definición tenemos que existe $r_1>0$ tal que para cualquier $x\in (x_0-r_1,x_0+r_1)$ ocurre que:
$$f(x)\le f(x_0).$$
O bien, si $x_0$ mínimo local de $f$ tenemos que existe $r_1>0$ tal que para cualquier $x\in (x_0-r_1,x_0+r_1)$ ocurre que:
$$f(x_0)\le f(x).$$
Consideremos ahora $h$ tal que:
$$|h|\le r_2=\text{min}\{r,r_1\}.$$
Veremos el caso en que $x_0$ es máximo local de $f$.
Caso 1: Supongamos que $x_0$ es máximo.
Si tenemos que $h>0$ se sigue que:
$$\begin{array}{rl}f(x_0+h)<f(x_0)& \Rightarrow f(x_0+h)-f(x_0)<0\\ & \Rightarrow \frac{f(x_0+h)-f(x_0)}{h}<0\\ & \Rightarrow \underset{h\to 0^{+}}{lim}\frac{f(x_0+h)-f(x_0)}{h}\le 0\end{array}$$

Ya que $f$ es derivable en $x_0$ entonces podemos afirmar la siguiente igualdad:
$$\underset{h\to 0^{+}}{lim}\frac{f(x_0+h)-f(x_0)}{h}=f^{\prime }(x_0).$$
$$\therefore f^{\prime }(x_0)\le 0.$$

Ahora bien, si tenemos que $h<0$ tenemos que:
$$\begin{array}{rl}f(x_0+h)-f(x_0)<0& \Rightarrow \frac{f(x_0+h)-f(x_0)}{h}>0\\ & \Rightarrow \underset{h\to 0^{-}}{lim}\frac{f(x_0+h)-f(x_0)}{h}\ge 0\end{array}$$
$$\therefore f^{\prime }(x_0)\ge 0.$$
$$\therefore 0\le f^{\prime }(x_0)\le 0.$$

Y así concluimos que $f^{\prime }(x_0)=0.$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

El Caso 2 considerando ahora que $x_0$ es mínimo se quedará como ejercicio de Tarea moral, para realizar la prueba se procede de manera análoga al caso que ya vimos.

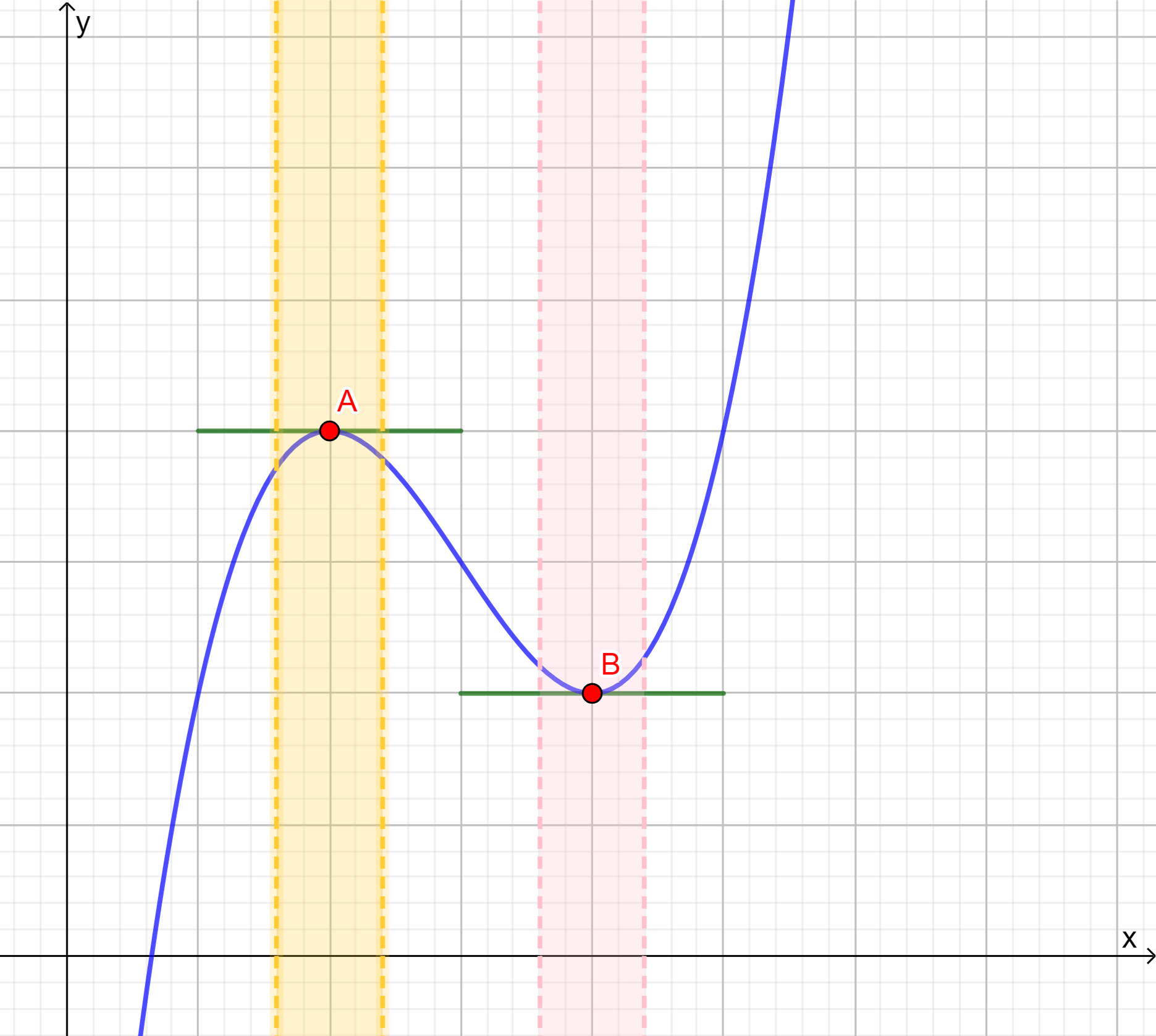
Gráficamente el resultado anterior se vería como sigue:

donde en el intervalo en el que se encuentra el punto $A$ la recta tangente a dicho punto tiene pendiente cero, es decir, es una recta horizontal. Observamos que para el intervalo (representado por la franja rosa) en el que se encuentra el punto $B$ tenemos una situación similar.

La derivada y la monotonía de las funciones

Teorema: Consideremos $f$ una función e $I$ un intervalo.

1. Si $f^{\prime }(x)>0$ para todo $x\in I\Rightarrow f$ es creciente en $I$.
2. Si $f^{\prime }(x)\ge 0$ para todo $x\in I\Rightarrow f$ es no decreciente en $I$.
3. Si $f^{\prime }(x)<0$ para todo $x\in I\Rightarrow f$ es decreciente en $I$.
4. Si $f^{\prime }(x)\le 0$ para todo $x\in I\Rightarrow f$ es no creciente en $I$.

Demostración 1:

Queremos probar que para cualesquiera $x_1,x_2\in I$ donde si $x_1<x_2$ entonces:
$$f(x_1)<f(x_2).$$

Así tomemos $x_1,x_2$ en el intervalo $I$ con $x_1<x_2$. Veamos que $[x_1,x_2]\subseteq I$ y que $f$ es derivable en $(x_1,x_2)\subseteq I$. Y además tenemos que $f$ es continua en $[x_1,x_2]\subseteq I$, aplicando el Teorema del valor medio para la derivada:
$\mathrm{\exists }\alpha \in (x_1,x_2)$ tal que $f^{\prime }(\alpha )=\frac{f(x_2)-f(x_1)}{x_2-x_1}$.
Por hipótesis tenemos que:
$$f^{\prime }(\alpha )=\frac{f(x_2)-f(x_1)}{x_2-x_1}>0.$$
Debido a que también supusimos $x_2-x_1>0$ para que se cumpla la desigualdad anterior necesariamente debe ocurrir que:
$$f(x_2)-f(x_1)>0\Rightarrow f(x_2)>f(x_1).$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

Criterio de la primera derivada

Teorema (Criterio de la primera derivada): Si $f^{\prime }(x_0)=0$ y existe $r>0$ tal que:

1. Para todo $x\in (x_0-r,x_0)$, $f^{\prime }(x)<0$ y para todo $x\in (x_0,x_0+r)$, $f^{\prime }(x)>0$
   $\Rightarrow x_0$ es mínimo local de $f$.
2. Para todo $x\in (x_0-r,x_0)$, $f^{\prime }(x)>0$ y para todo $x\in (x_0,x_0+r)$, $f^{\prime }(x)<0$
   $\Rightarrow x_0$ es máximo local de $f$.

Demostración 1:

Sea $x\in (x_0-r,x_0)$ por hipótesis tenemos que $f^{\prime }(x)<0$. Aplicando el teorema anterior afirmamos que $f$ es decreciente en $(x_0-r,x_0)$, así para cualquier $x<x_0$ en $(x_0-r,x_0)$:
$$f(x)>f(x_0).$$

Ahora tomando $x\in (x_0,x_0+r)$ tenemos que $f^{\prime }(x)>0$. Y por el teorema anterior sabemos que $f$ es creciente en el intervalo $(x_0,x_0+r)$. Por definición para cualquier $x>x_0$ en $(x_0,x_0+r)$ ocurre que:
$$f(x_0)<f(x).$$
De lo anterior podemos concluir que para toda $x\in (x_0-r,x_0)\cup (x_0,x_0+r)=(x_0-r,x_0+r)$ se cumple la desigualdad:
$$f(x_0)<f(x).$$
que es justo la definición de $x_0$ mínimo local de $f$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◻"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fb.svg">}$

A continuación veremos ejemplos donde aplicaremos los teoremas anteriores para localizar los máximos y mínimos de una función, como los intervalos donde es creciente o decreciente.

Ejemplo 1

Encuentra los puntos críticos de la siguiente función y determina si se trata de un máximo o un mínimo:
$$f(x)=(x-1{)}^2(x+1{)}^3$$

Solución:

Para encontrarlos seguiremos los siguientes pasos:
Paso 1: Hallamos la primera derivada de la función $f$.
$$\begin{array}{rl}{f}^{\prime }(x)& =2(x-1)(x+1{)}^3+3(x+1{)}^2(x-1{)}^2\\ & =(x-1)[2(x+1{)}^3+3(x+1{)}^2(x-1)]\\ & =(x-1)(x+1{)}^2[2(x+1)+3(x-1)]\\ & =(x-1)(x+1{)}^2[2x+2+3x+3]\\ & =(x-1)(x+1{)}^2(5x-1)\\ \therefore f^{\prime }(x)& =(x-1)(x+1{)}^2(5x-1)\end{array}$$

Paso 2: Igualamos la derivada a cero para encontrar los puntos críticos.
$$f^{\prime }(x)=0\iff (x-1)(x+1{)}^2(5x-1)=0$$
El producto anterior lo cumple cuando:
$$\begin{array}{rlrlr}(x+1{)}^2=0& & \text{o}5x-1=0& & \text{o}x-1=0\\ \sqrt{(x+1{)}^2}=\sqrt{0}& & \text{o}5x=1& & \text{o}x=1\\ x+1=0& & \text{o}x=\frac{1}{5}\\ x=-1\end{array}$$

Por lo que debemos determinar para $x=1$, $x=-1$ y $x=\frac{1}{5}$ si se trata de un máximo, un mínimo o ninguno de los dos.

Paso 3: Para determinar si es un máximo o mínimo, aplicando el Criterio de la primera derivada debemos sustituir en la primera derivada un valor $x_1<x$ para determinar si $f^{\prime }(x_1)$ es positiva o negativa. De igual modo debemos evaluar una $x<x_2$ y obtener si $f^{\prime }(x_2)$ es positiva o negativa.

Comencemos con $x=1$:
Si tomamos $x<1$ y sustituimos en $f^{\prime }(x)=5(x-1)(x+1{)}^2(x-\frac{1}{5})$ a $x_1=\frac{1}{2}$ en la derivada
$$\begin{array}{rl}{f}^{\prime }\left(\frac{1}{2}\right)& =5(\frac{1}{2}-1){(\frac{1}{2}+1)}^2(\frac{1}{2}-\frac{1}{5})\\ \text{(que es negativo)}& & =5(-\frac{1}{2}){\left(\frac{3}{2}\right)}^2\left(\frac{3}{10}\right)\end{array}$$
Ahora para $x>1$ evaluamos $x_2=2$
$$\begin{array}{rl}{f}^{\prime }(2)& =5(2-1)(2+1{)}^2(2-\frac{1}{5})\\ \text{(que es positivo)}& & =5(1)(3{)}^2\left(\frac{9}{5}\right)\end{array}$$
Ya que la derivada pasó de ser negativa a positiva tenemos que cuando $x=1$ la función tiene un mínimo.
$\therefore p_1=(1,0)$ es mínimo de $f$.

Continuemos con $x=-1$:
Para $x<-1$ tomaremos $x_1=-2$.
$$\begin{array}{rl}{f}^{\prime }(-2)& =5(-2-1)(-2+1{)}^2(-2-\frac{1}{5})\\ \text{(que es positivo)}& & =5(-3)(-1{)}^2(-\frac{11}{5})\end{array}$$

Y para $x>-1$ consideramos ahora $x_2=-\frac{1}{2}$.
$$\begin{array}{rl}{f}^{\prime }(-\frac{1}{2})& =5{(-\frac{1}{2}-1)}^2(-\frac{1}{2}-\frac{1}{5})\\ \text{(que es positivo)}& & =5(-\frac{3}{2}){\left(\frac{1}{2}\right)}^2(-\frac{7}{10})\end{array}$$

Debido a que la derivada no presenta cambio de signo, cuando $x=-1$ no es máximo ni mínimo.

Finalmente para $x=\frac{1}{5}$ análogamente procedemos:
Cuando $x<\frac{1}{5}$ sustituiremos $x_1=\frac{1}{6}$.
$$\begin{array}{rl}{f}^{\prime }\left(\frac{1}{6}\right)& =5(\frac{1}{6}-1){(\frac{1}{6}+1)}^2(\frac{1}{6}-\frac{1}{5})\\ \text{(que es positivo)}& & =5(-\frac{5}{6}){\left(\frac{7}{6}\right)}^2(-\frac{1}{30})\end{array}$$

Ahora bien para $x>\frac{1}{5}$ evaluaremos $x_2=\frac{1}{2}$.
$$\begin{array}{rl}{f}^{\prime }\left(\frac{1}{2}\right)& =5(\frac{1}{2}-1){(\frac{1}{2}+1)}^2(\frac{1}{2}-\frac{1}{5})\\ \text{(que es negativo)}& & =5(-\frac{1}{2})\left(\frac{3}{2}\right)\left(\frac{3}{10}\right)\end{array}$$

Vemos que la derivada pasó de ser positiva a ser negativa, por lo tanto, cuando $x=\frac{1}{5}$ la función $f$ tiene un máximo.
$\therefore p_2=(0.2,1.10)$ es un máximo de $f$.

Ejemplo 2

Hallar los intervalos donde es creciente o decreciente la siguiente función:
$$f(x)=4x^3+3x^2-6x.$$

Solución:
Comenzaremos derivando la función y simplificando
$$\begin{array}{rl}{f}^{\prime }(x)& =12x^2+6x-6\\ & =6x^2+x-1\\ & =(x-\frac{1}{2})(x+1)\end{array}$$

Sabemos que cuando $f^{\prime }(x)>0$ la función es creciente, por ello veremos qué valores satisfacen la siguiente desigualdad:
$$(x-\frac{1}{2})(x+1)>0.$$
El producto anterior cumple ser positivo cuando
Caso 1:
$$\begin{array}{rlr}x-\frac{1}{2}>0& & \text{y}x+1>0\\ x>\frac{1}{2}& & \text{y}x>-1\end{array}$$
Por lo que el intervalo solución para este caso es: $(\frac{1}{2},\mathrm{\infty })$.

Caso 2:
$$\begin{array}{rlr}x-\frac{1}{2}<0& & \text{y}x+1<0\\ x<\frac{1}{2}& & \text{y}x<-1\end{array}$$
Así el intervalo solución es: $(-\mathrm{\infty },-1)$.

Concluimos que los intervalos donde $f$ es creciente son:
$$(-\mathrm{\infty },-1)\cup (\frac{1}{2},\mathrm{\infty }).$$

Para encontrar donde la función es decreciente debemos trabajar con la desigualdad $f^{\prime }(x)<0$, que sería:
$$(x-\frac{1}{2})(x+1)<0.$$
Lo anterior se cumple en los siguientes casos:
Caso 3:
$$\begin{array}{rlr}x-\frac{1}{2}>0& & \text{y}x+1<0\\ x>\frac{1}{2}& & \text{y}x<-1\end{array}$$
Vemos que la solución de este caso es vacía.

Caso 4:
$$\begin{array}{rlr}x-\frac{1}{2}<0& & \text{y}x+1>0\\ x<\frac{1}{2}& & \text{y}x>-1\end{array}$$
El intervalo que cumple lo anterior es $(-1,\frac{1}{2})$.

De los casos anteriores tenemos que $f$ es decreciente en el intervalo:
$$(-1,\frac{1}{2})$$

Más adelante

En la siguiente entrada seguiremos trabajando con los máximos y mínimos de funciones, por lo que te presentaremos una herramienta más para poder localizarlos: el Criterio de la segunda derivada. También veremos cómo determinar las regiones de concavidad o convexidad de una función y sus puntos de inflexión.

Tarea moral

• Da la demostración del teorema para el caso en que $x_0$ es un mínimo local de $f$.
• Prueba los siguientes puntos:
  • Si $f^{\prime }(x)\ge 0$ para todo $x\in I\Rightarrow f$ es no decreciente en $I$.
  • Si $f^{\prime }(x)<0$ para todo $x\in I\Rightarrow f$ es decreciente en $I$.
  • Si $f^{\prime }(x)\le 0$ para todo $x\in I\Rightarrow f$ es no creciente en $I$.
• Determina si los siguientes enunciados son verdaderos o falsos. De ser verdadero da la demostración correspondiente, de lo contrario da un contraejemplo:
  • Si $f$ es una función creciente, derivable y continua en un intervalo $I\Rightarrow f^{\prime }(x)>0$ para toda $x\in I$.
  • Si $f$ es una función estrictamente creciente, continua y derivable en $I\Rightarrow f^{\prime }(x)>0$ para toda $x\in I$.
• Realiza la gráfica de la función:
  $$f(x)=\frac{1}{(x-1{)}^2}+1.$$
  Determinando los intervalos donde $f$ es creciente o decreciente.
  Señalando si es que existen:
  • máximos y mínimos (locales y globales).
  • los valores $x$ donde $f(x)=0$.
  • $\underset{x\to {\mathrm{\infty }}^{+}}{lim}f(x)$.
  • $\underset{x\to {\mathrm{\infty }}^{-}}{lim}f(x)$.

Entradas relacionadas

• Ir a: Cálculo Diferencial e Integral I
• Entrada anterior del curso: Cálculo Diferencial e Integral I: Rectas tangente y normal a una curva.
• Entrada siguiente del curso: Cálculo Diferencial e Integral I: Localización de máximos y mínimos. Regiones de convexidad y puntos de inflexión.
• Resto de cursos: Cursos

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»