Introducción

En la sección anterior vimos como calcular el volumen de una superficie de revolución por el método de capas cilíndricas, ahora, en esta entrada veremos como calcular el área de una superficie de revolución.

Área de una superficie de revolución

Consideremos una región delimitada por el eje $x$, las rectas $x=a$ y $x=b$ y la curva que tiene como función $y=f(x)$, continua en el intervalo $[a,b]$, giramos esta región alrededor del eje $x$ obteniendo una superficie de revolución como en la figura $(1)$.

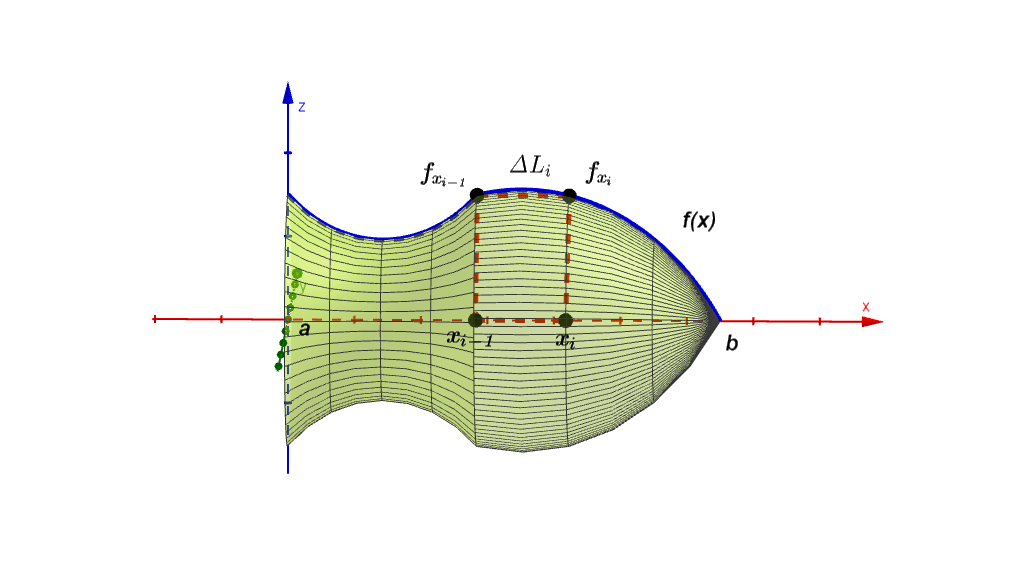
Dividimos el intervalo $[a,b]$ en $n$ subintervalos en donde el i-ésimo subintervalo es $[x_{i-1},x_i]$ y sea $\mathrm{\Delta }{S}_i$ el valor del área superficial del i-ésimo subintervalo $[x_{i-1},x_i]$ lo podemos calcular viéndolo como un tronco cónico (encerrado en líneas puntuadas, figura $(1)$) en donde su área de superficial es:

$$\begin{array}{}\text{(1)}& S=\pi (r_1+r_2)g\end{array}$$

Donde $g$ es la generatriz del tronco cónico, $r_1$ y $r_2$ son los radios respecto al eje de rotación.

Para dar correspondencia a la figura $(1)$, sea $g_i=\mathrm{\Delta }{L}_i$ la generatriz del i-esimo tronco cónico, que se aproxima a la gráfica $y=f(x)$ como se muestra en la figura $(1)$ en el intervalo $[x_{i-1},x_i]$, por lo que el área superficial del i-esimo tronco cónico designado como $\mathrm{\Delta }{S}_i$, lo podemos aproximar mediante la relación $(1)$ como:

$$\mathrm{\Delta }{S}_i\approx \pi (f(x_{i-1})+f(x_i))\mathrm{\Delta }{L}_i$$

Pero $\mathrm{\Delta }{L}_i$ lo podemos aproximar por la definición de la longitud de arco en el intervalo $[x_{i-1},x_i]$, así:

$$\mathrm{\Delta }{L}_i\approx \sqrt{1+(f^{\prime }(x_i{)}^2)}\mathrm{\Delta }x$$

Con $\mathrm{\Delta }x=x_i-x_{i-1}$, por tanto:

$$\begin{array}{}\text{(2)}& \mathrm{\Delta }{S}_i\approx \pi (f(x_{i-1})+f(x_i))\sqrt{1+(f^{\prime }(x_i{)}^2)}\mathrm{\Delta }x\end{array}$$

Por otro lado, en el curso de Cálculo I, se vio el desarrollo de Taylor de una función $f(x)$, por lo que la definición del desarrollo en Taylor está dado de la forma:

$$y(x+h)\approx y(x)+h{y}^{\prime }(x)+\frac{h^2{y}^{\prime \prime }(x)}{2!}+\dots .$$

Aplicando lo anterior para $f(x_{i-1})$ suponiendo que ${\mathrm{\Delta }}^{n}x$ es pequeño respecto al término $\mathrm{\Delta }x$, se tiene que:

$$f(x_{i-1})=f(x_{i-1}+x_i-x_i)=f(x_i-\mathrm{\Delta }x)\approx f(x_i)-f^{\prime }(x_i)\mathrm{\Delta }x$$

Substituyendo en $\mathrm{\Delta }{S}_i$ $(2)$, tenemos que:

$$\mathrm{\Delta }{S}_i\approx \pi \sqrt{1+(f^{\prime }(x_i{)}^2)}(f(x_{i-1})+f(x_i))\mathrm{\Delta }x=\pi \sqrt{1+(f^{\prime }(x_i{)}^2)}\mathrm{\Delta }x(f(x_i)-f^{\prime }(x_i)\mathrm{\Delta }x+f(x_i))$$

$$=\pi \sqrt{1+(f^{\prime }(x_i{)}^2)}\mathrm{\Delta }x(2f(x_i)-f^{\prime }(x_i)\mathrm{\Delta }x)=\pi \sqrt{1+(f^{\prime }(x_i{)}^2)}\mathrm{\Delta }x2f(x_i)-\pi \sqrt{1+(f^{\prime }(x_i{)}^2)}{\mathrm{\Delta }}^{2}x{f}^{\prime }(x_i)$$

Observemos que cuando $n$ es demasiado grande el termino ${\mathrm{\Delta }}^{2}x$ es pequeño respecto al término $\mathrm{\Delta }x$, por lo que para $n$ lo suficientemente grande podemos despreciar el termino ${\mathrm{\Delta }}^{2}x$, así:

$$\mathrm{\Delta }{S}_i\approx 2\pi f(x_i)\sqrt{1+(f^{\prime }(x_i{)}^2)}\mathrm{\Delta }x$$

Sumando todas las $n$ áreas superficiales y tendiendo $n\to \mathrm{\infty }$ tenemos que el área de superficie $A_s$ es:

$$A_s=\underset{n\to \mathrm{\infty }}{lim}\sum _{i=1}^n\mathrm{\Delta }{S}_i=\underset{n\to \mathrm{\infty }}{lim}\sum _{i=1}^{n}2\pi f(x_i)\sqrt{1+(f^{\prime }(x_i{)}^2)}\mathrm{\Delta }x$$

Se define el área superficial de un sólido de revolución si una función $f(x)\ge 0$ es continua en el intervalo $[a,b]$ y gira alrededor del eje $x$ como:

$$\begin{array}{}\text{(3)}& A_s={\int }_a^{b}2\pi y\sqrt{1+{\left(\frac{dy}{dx}\right)}^2}dx={\int }_a^{b}2\pi f(x)\sqrt{1+(f^{\prime }(x{)}^2)}dx\end{array}$$

Análogamente, se define el área superficial de un sólido de revolución alrededor del eje $y$ como:

$$\begin{array}{}\text{(4)}& A_s={\int }_c^{d}2\pi x\sqrt{1+{\left(\frac{dx}{dy}\right)}^2}dy={\int }_c^{d}2\pi f(y)\sqrt{1+(f^{\prime }(y{)}^2)}dy\end{array}$$

Ejemplos

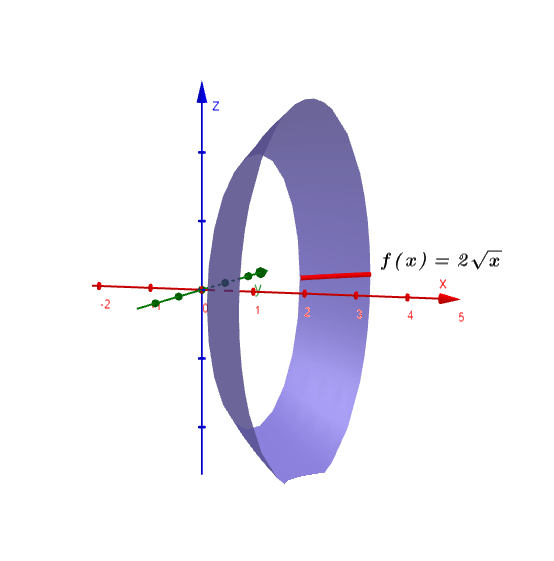
• Determinar el área de la superficie generada al hacer girar la curva $2\sqrt{x}$, donde $1\le x\le 2$ alrededor del eje x.

Tenemos que $a=1$, $b=2$ y la curva que tiene como función $f(x)=2\sqrt{x}$, derivando obtenemos:

$$\frac{dy}{dx}f(x)=\frac{1}{\sqrt{x}}$$

La gráfica la vemos en la figura $(2)$, así, utilizamos la relación $(3)$ y calculamos el área como:

$$S={\int }_1^{2}2\pi (2\sqrt{x})\sqrt{1+{\left(\frac{1}{\sqrt{x}}\right)}^2}dx$$

Vemos que:

$$\sqrt{1+{\left(\frac{1}{\sqrt{x}}\right)}^2}=\sqrt{1+\frac{1}{x}}=\sqrt{\frac{x+1}{x}}=\frac{\sqrt{x+1}}{\sqrt{x}}$$

Sustituyendo esta expresión:

$$S={\int }_1^{2}2\pi (2\sqrt{x})\frac{\sqrt{x+1}}{\sqrt{x}}dx={\int }_1^{2}4\pi \sqrt{x+1}dx$$

Utilizando el método de sustitución tenemos que esta integral nos da por resultado:

$$S=4\pi \frac{2}{3}[(x+1{)}^{2/3}]{|}_1^2=\frac{8\pi }{3}(3\sqrt{3}-2\sqrt{2})$$

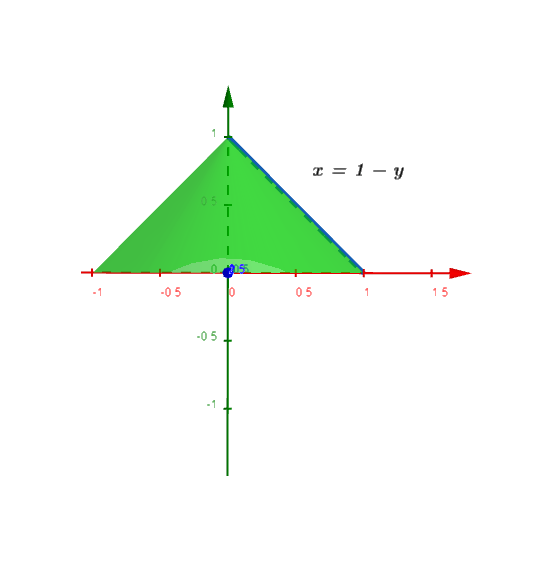
• El segmento de recta $x=1-y$, $0\le y\le 1$ se hace girar alrededor del eje $y$ para generar el cono de la figura $(3)$, determinar el área de su superficie lateral (la cual excluye el área de la base).

Tenemos que $c=0$, $d=1$ y la función de la curva:

$$x=1-y\Rightarrow \frac{dx}{dy}=-1\Rightarrow \sqrt{1+{\left(\frac{dx}{dy}\right)}^2}=\sqrt{1+(-1{)}^2}=\sqrt{2}$$

Utilizamos la relación $(4)$ y calculamos el área superficial como:

$$S={\int }_0^{1}2\pi f(y)\sqrt{2}dy={\int }_0^{1}2\pi (1-y)\sqrt{2}dy=2\pi \sqrt{2}[y-\frac{y^2}{2}]{|}_0^1=2\pi \sqrt{2}(1-\frac{1}{2})=\pi \sqrt{2}$$

Tarea moral

Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionados con el tema visto.

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. El segmento de recta $y=\frac{x}{2}$, $0\le x\le 4$ se hace girar alrededor del eje x para generar un cono, determinar el área de su superficie lateral.
2. Un segmento de recta $y=\sqrt{2}$, $\frac{3}{4}\le x\le \frac{15}{4}$ se hace girar alrededor del eje x determinar el área de su superficie.
3. El segmento de recta $x=\frac{y^3}{3}$, $0\le y\le 1$ se hace girar alrededor del eje y determinar el área de su superficie.
4. Un segmento de recta $x=2\sqrt{4-y}$, $0\le y\le \frac{15}{4}$ se hace girar alrededor del eje y determinar el área de su superficie.
5. El segmento de recta $y=\sqrt{x+1}$, $1\le x\le 5$ se hace girar alrededor del eje x determinar el área de su superficie.

Más adelante…

En esta entrada vimos como calcular el área de superficie de un sólido generado a partir de una curva respecto de un eje. En la siguiente sección trabajaremos con un teorema relacionado con el cálculo de estas áreas llamado el teorema de Pappus-Guldinus.

Entradas relacionadas

• Ir a Cálculo Diferencial e Integral II.
• Entrada anterior del curso: Cálculo Diferencial e Integral II: Cálculo de volúmenes por medio de casquillos cilíndricos – El blog de Leo (nekomath.com)
• Siguiente entrada del curso: Cálculo Diferencial e Integral II: Teorema de Pappus-Guldinus – El blog de Leo (nekomath.com)