Introducción
En la entrada anterior abordamos el enfoque frecuentista de la probabilidad. El siguiente enfoque que veremos requiere de algunas herramientas adicionales. Por ello, el propósito de esta sección es hacer todos los preparativos para estudiar la siguiente medida de probabilidad importante: la probabilidad clásica. Este último enfoque se utiliza para el caso en el que $\Omega$, el espacio muestral, es finito, y se basa en la cardinalidad de $\Omega$ y la de sus subconjuntos. En consecuencia, es necesario que sepas contar la cantidad de elementos que tiene cualquier subconjunto de $\Omega$ que se te pida.
No demostraremos la validez de las propiedades para conjuntos en esta entrada, pues se trata de propiedades de conjuntos finitos. Por ello, puedes consultar nuestras notas de Álgebra Superior I en caso de que las necesites. Esta parte del curso está basada principalmente en el primer capítulo del libro Discrete and Combinatorial Mathematics: An Applied Introduction (5ᵃ edición) de Ralph P. Grimaldi.
El principio de conteo de la suma
Comenzaremos enunciando algunos principios de conteo asociados a la realización de tareas. Estos principios pueden expresarse en términos de cardinalidades de conjuntos.
Principio de la suma. Si una tarea puede realizarse de $m$ formas distintas, y otra tarea puede realizarse de $n$ formas distintas, y las dos tareas no se pueden hacer simultáneamente, entonces se puede realizar alguna de las dos tareas de $m + n$ maneras distintas.
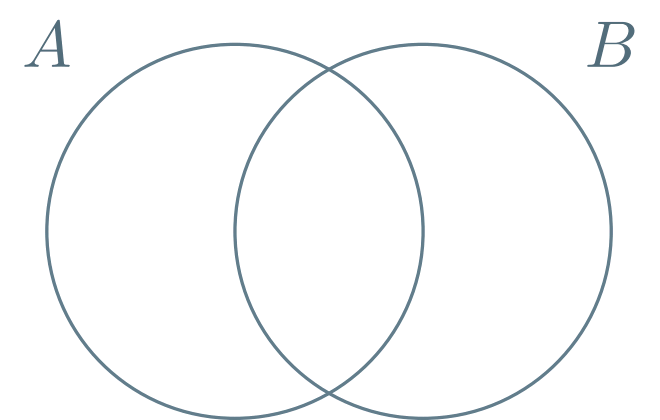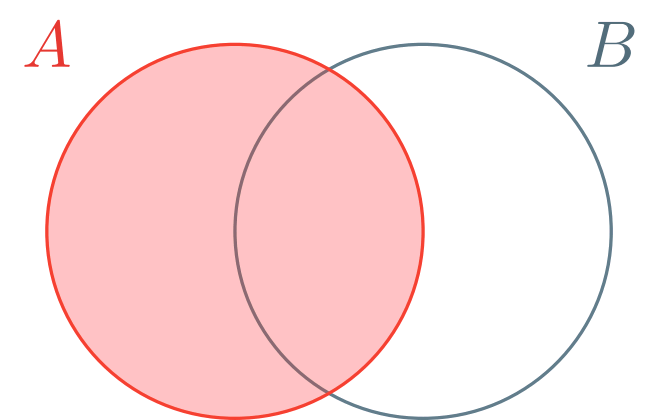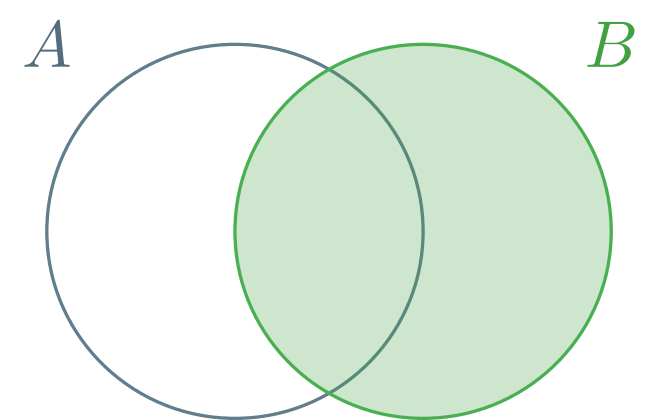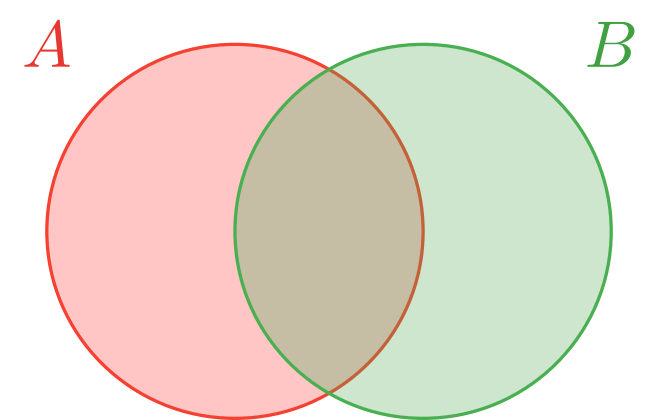
En términos de conjuntos. Si $A$, $B$ son conjuntos finitos tales que $A \cap B = \emptyset$, entonces
\[ | A \cup B | = |A| + |B|. \]
Donde $|A|$ es la cardinalidad (número de elementos) del conjunto $A$.
Ejemplo. En la biblioteca de la Facultad de Ciencias hay $25$ libros sobre probabilidad y $15$ libros sobre álgebra moderna. Así, por el principio de la suma, un alumno de la Facultad de Ciencias puede elegir de entre $25 + 15 = 40$ libros para aprender sobre cualquiera de estos dos temas.
El principio de la suma puede extenderse a más de dos tareas, siempre y cuando se cumpla que ningún par de tareas pueda ocurrir simultáneamente. En términos de conjuntos, se tiene que para cualesquiera $A_{1}$, $A_{2}$, …, $A_{k}$ conjuntos que son ajenos dos a dos. Entonces se cumple que
\[ {\left| \bigcup_{i=1}^{k} A_{i} \right|} = \sum_{i=1}^{k} |A_{i}| \]
Precisamente, que los conjuntos sean ajenos dos a dos se interpreta como que ningún par de tareas puede realizarse simultáneamente.
Ejemplo. En la sección de ciencias de la computación de la biblioteca de la Facultad de Ciencias de la UNAM hay $7$ libros sobre C++, $6$ libros sobre Java, y $5$ libros sobre Python. En consecuencia, por el principio de la suma, una alumna de la facultad de ciencias tiene $7+6+5=18$ libros a elegir para comenzar a aprender algún lenguaje de programación.
También podemos precisar qué ocurre cuando $A$ y $B$ son finitos y no son ajenos. Primero, veamos cuando $B \subseteq A$. Como $B \subseteq A$, se cumple que $A = B \cup (A \smallsetminus B)$. Observa que $B$ y $A \smallsetminus B$ son conjuntos ajenos, por lo que
\[ |A| = |B \cup (A \smallsetminus B)| = |B| + |A \smallsetminus B|. \]
Y como la cardinalidad de un conjunto finito es un número natural, se tiene que $|B| \leq |A|$. En conclusión, si $A \subseteq B$, entonces $|B| \leq |A|$. Ahora, sabemos que para cualesquiera conjuntos finitos $A$ y $B$, los conjuntos $A$ y $B \smallsetminus A$ son ajenos, y que $A \cup B = A \cup (B \smallsetminus A)$, por lo que
\[ |A \cup B| = |A \cup (B \smallsetminus A)| = |A| + |B \smallsetminus A|, \]
y como $B \smallsetminus A \subseteq B$, se tiene que $|B\smallsetminus A| \leq |B|$, y así
\[ |A \cup B| = |A| + |B \smallsetminus A| \leq |A| + |B|. \]
En conclusión, la cardinalidad es subaditiva. De hecho, esta última propiedad se cumple para cualquier $n \in \mathbb{N}^{+}$ y cualesquiera $A_{1}$, $A_{2}$, …, $A_{n}$ conjuntos finitos:
\[ {\left| \bigcup_{i=1}^{n} A_{i} \right|} \leq \sum_{i=1}^{n} |A_{i}|. \]
Ejemplo. Una profesora de la facultad de ciencias tiene $8$ libros sobre Probabilidad en su colección, mientras que uno de sus colegas tiene $5$. Si denotamos por $m$ al número de libros diferentes sobre Probabilidad que tienen en su posesión, se cumple que
\[ 8 \leq m \leq 13, \]
pues $m$ será $8$ si el colega de la profesora tiene los mismos libros que ella (y así, el número de libros distintos que tienen en su posesión es $8$). Por otro lado, por el principio de la suma, $m$ puede tomar un valor máximo de $8 + 5 = 13$ en el caso de que los libros de la profesora y de su colega son todos distintos.
En la entrada de propiedades de una medida de probabilidad vimos un resultado conocido como el principio de inclusión-exclusión. Resulta que este principio es cierto también para la cardinalidad de conjuntos finitos. Es decir, que para cualesquiera $A$ y $B$ conjuntos finitos se cumple que
\[ |A \cup B| = |A| + |B|− |A \cap B|. \]
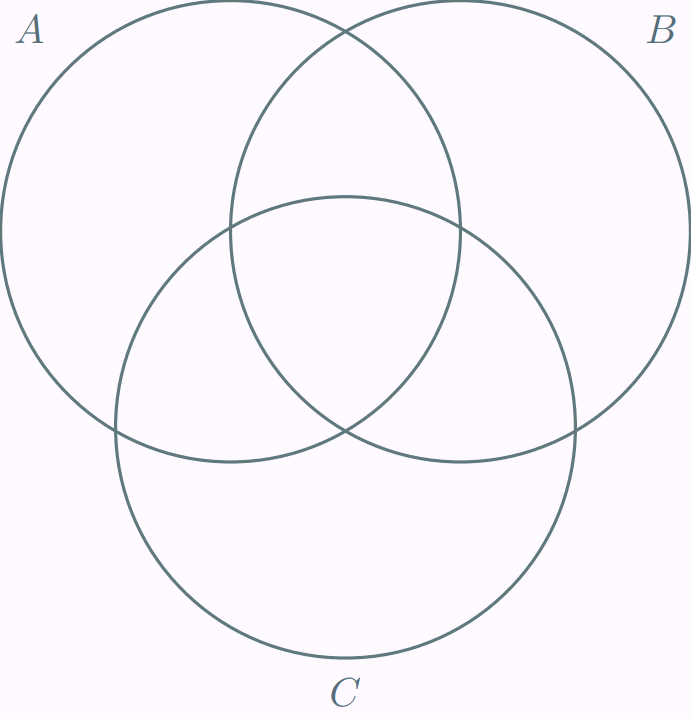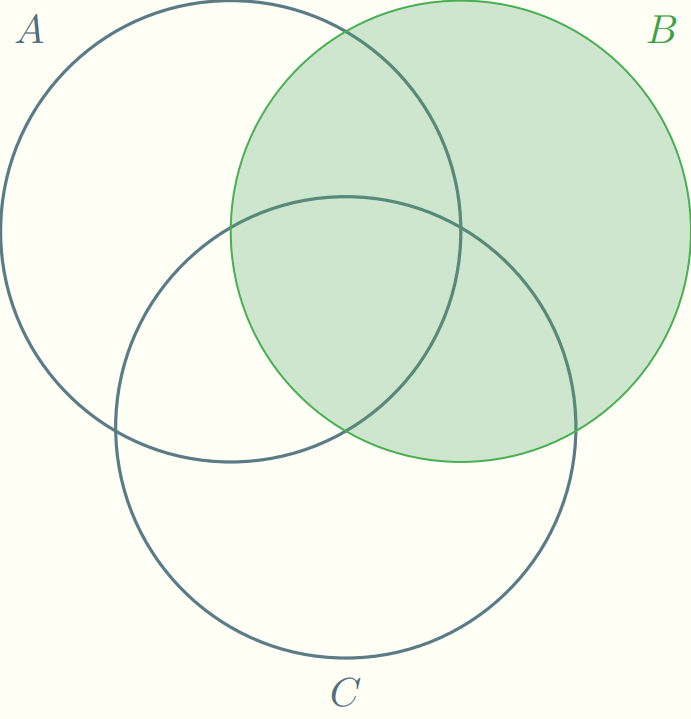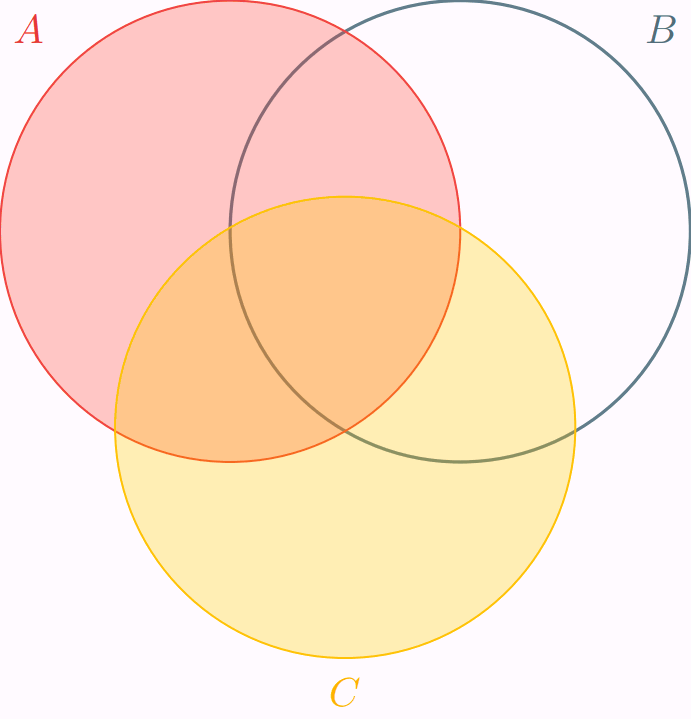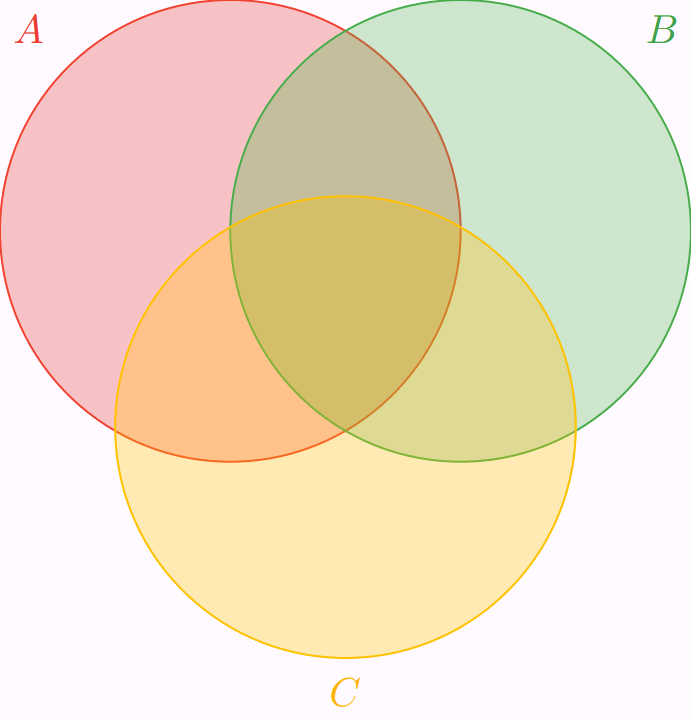
Más aún, para cualquier $n \in \mathbb{N}^{+}$ y cualesquiera $A_{1}$, $A_{2}$, …, $A_{n}$ conjuntos finitos se cumple que
\[ {\left| \bigcup_{i=1}^{n} A_{i} \right|} = \sum_{i=1}^{n}|A_{i}| − \sum_{i<j}|A_{i} \cap A_{j}| + \sum_{i<j<k} |A_{i} \cap A_{j} \cap A_{k}| − \cdots + (-1)^{n+1}{\left|\bigcap_{i=1}^{n} A_{i} \right|}. \]
Por ejemplo, para $n=3$ y para cualesquiera $A_{1}$, $A_{2}$, $A_{3}$ conjuntos finitos, se tiene que
\[ |A_{1} \cup A_{2} \cup A_{3}| = |A_{1}| + |A_{2}| + |A_{3}| − |A_{1} \cap A_{2}| − |A_{1} \cap A_{3}| − |A_{2} \cap A_{3}| + |A_{1} \cap A_{2} \cap A_{3}|. \]
Ejemplo. Le pedimos a tres aficionados al rock progresivo que nos dijeran sus $5$ bandas favoritas de este género musical. Sus listas son las siguientes:
Aficionado 1 ($A_{1}$)
- Pink Floyd.
- Genesis.
- Marillion.
- Rush.
- Riverside.
Aficionado 2 ($A_{2}$)
- King Crimson.
- Yes.
- Genesis.
- Rush.
- Pink Floyd.
Aficionado 3 ($A_{3}$)
- Jethro Tull.
- King Crimson.
- Änglagård.
- Anekdoten.
- Yes.
Si decides escoger una banda de las que mencionaron estas tres personas, ¿cuántas opciones distintas existen? En otras palabras, ¿cuál es la cardinalidad de $A_{1} \cup A_{2} \cup A_{3}$? Para verlo, podemos valernos del principio de inclusión-exclusión. Primero, veamos los elementos que tienen en común las listas al compararlas dos a dos:
$A_{1} \cap A_{2}$
- Pink Floyd.
- Genesis.
- Rush.
$A_{1} \cap A_{3}$
No tienen elementos en común.
$A_{2} \cap A_{3}$
- King Crimson.
- Yes.
En consecuencia, $|A_{1} \cap A_{2}| = 3$, $|A_{1} \cap A_{3}| = 0$ y $|A_{2} \cap A_{3}| = 2$. Luego, observa que no hay elementos en común entre las tres listas, por lo que $|A_{1} \cap A_{2} \cap A_{3}| = 0$. Entonces tenemos que
\begin{align*} |A_{1} \cup A_{2} \cup A_{3}| &= |A_{1}| + |A_{2}| + |A_{3}| − |A_{1} \cap A_{2}| − |A_{1} \cap A_{3}| − |A_{2} \cap A_{3}| + |A_{1} \cap A_{2} \cap A_{3}| \\ &= 5 + 5 + 5 − 3 − 0 − 2 + 0 \\ &= 15 − 5 \\ &= 10. \end{align*}
Por lo tanto, existen $10$ opciones distintas a elegir entre las bandas que mencionaron las tres personas.
El principio de conteo del producto
Ahora, ¿qué pasa cuando tenemos dos tareas y queremos hacerlas de forma consecutiva, en orden? Por ejemplo, imagina que tienes $3$ camisas distintas y $4$ pantalones distintos. ¿De cuántas maneras posibles puedes ponerte primero una camisa y luego un pantalón? Por cada una de las $3$ de camisas habrá $4$ pantalones distintos a escoger.

En consecuencia, a la primera camisa le corresponden $4$ pantalones, a la segunda también, y a la tercera lo mismo. Por ello, el número de maneras posibles de ponerte primero una camisa y luego un pantalón serían $4 + 4 + 4 = 3 \cdot 4 = 12$.
Podemos verlo en términos de conjuntos. Sean $C = \{ c_{1}, c_{2}, c_{3} \}$ el conjunto de las camisas y $P = \{ p_{1}, p_{2}, p_{3}, p_{4} \}$ el conjunto de los pantalones. Podemos representar la idea de tomar primero una camisa y luego un pantalón a través del producto cartesiano de estos dos conjuntos:
\begin{align} C \times D = \begin{Bmatrix} (c_1,p_1), & (c_1, p_2), & (c_1, p_3), & (c_1, p_4) \\ (c_2,p_1), & (c_2, p_2), & (c_2, p_3), & (c_2, p_4) \\ (c_3,p_1), & (c_3, p_2), & (c_3, p_3), & (c_3, p_4) \end{Bmatrix}, \end{align}
observa que cada par ordenado representa cada una de las combinaciones de camisa y pantalón que puedes escoger. Por ello, $|C \times D|$ es el número total de combinaciones de camisa y pantalón posibles, que resulta ser $|C \times D| = |C||D| = 3 \cdot 4 = 12$. Además, observa que $C \times D$ representa precisamente la idea de que primero se escoge una camisa, y en segundo lugar se escoge el pantalón. Por otro lado, el conjunto $D \times C$ representa la idea de escoger primero el pantalón y después la camisa. Observa que esto no afecta el número total de combinaciones posibles.
La discusión anterior da lugar a nuestro segundo principio básico de conteo.
Principio del producto. Si una tarea puede dividirse en dos etapas y hay $m$ resultados posibles para la primera etapa y para cada una de estas etapas hay $n$ resultados posibles para la segunda etapa, entonces la tarea puede ser realizada, en el orden acordado, de $m n$ maneras distintas.
En términos de conjuntos. Para cualesquiera $A$ y $B$ conjuntos finitos se cumple que
\[ |A \times B| = |A||B|. \]
Ejemplo. Se lanzan dos dados distintos sobre una mesa. El primero tiene $6$ caras, y el segundo tiene $8$ caras. En consecuencia, esta actividad tiene $6 \cdot 8 = 48$ resultados posibles.
Ejemplo. El principio del producto puede extenderse a más de dos etapas en una misma tarea. Por ejemplo, considera la manufactura de placas para automóviles que consisten de $2$ letras seguidas de $4$ dígitos.

- Si no ponemos restricciones a la combinación de caracteres que lleva cada placa, entonces hay $26 \cdot 26 \cdot 10 \cdot 10 \cdot 10 \cdot 10 = 6{,}760{,}000$ placas posibles, pues hay $26$ letras en el alfabeto (sin considerar a la ‘ñ’) y $10$ dígitos del $0$ al $9$.
- Podemos restringir las combinaciones que admitimos en una placa. Si no permitimos que tenga letras repetidas, entonces la parte que corresponde a las letras tiene $26 \cdot 25$ combinaciones posibles. ¿Por qué $26 \cdot 25$ y no $26 \cdot 26$ como en el caso anterior? Precisamente porque al escoger la primera letra, la segunda no puede ser la misma, por lo que sólamente se puede escoger alguna de las $25$ restantes, que son distintas de la que ya se escogió. En consecuencia, hay $26 \cdot 25 \cdot 10 \cdot 10 \cdot 10 \cdot 10 = 6{,}500{,}000$ combinaciones de letras y dígitos en los que no se repiten las letras.
- Por otro lado, ¿cuántas placas hay sin dígitos repetidos? En este caso, sí permitimos que las letras se repitan, así que la parte correspondiente a las letras es $26 \cdot 26$. Por otro lado, en los dígitos, queremos que no haya dígitos repetidos, así que el número de cadenas de dígitos admisibles es $10 \cdot 9 \cdot 8 \cdot 7$. Esto se debe a que para el primer dígito se tienen $10$ opciones para escoger. Luego, al haber fijado el primero, el segundo está limitado a no ser el mismo que el primero, por lo que se puede escoger alguno de $9$ dígitos restantes. Después, el tercer dígito debe de ser distinto de los dos primeros, por lo que se escoge alguno de $8$ dígitos restantes. Finalmente, el cuarto dígito debe de ser distinto de los otros tres, por lo que se debe de escoger alguno de $7$ dígitos que quedan. En conclusión, hay $26 \cdot 26 \cdot 10 \cdot 9 \cdot 8 \cdot 7 = 3{,}407{,}040$ placas en las que los dígitos son todos distintos.
- Por último, ¿cuántas placas hay sin repeticiones? Es decir, que ninguno de los símbolos (letras o dígitos) se repite. En este caso, se tienen $26 \cdot 25 \cdot 10 \cdot 9 \cdot 8 \cdot 7 = 3{,}276{,}000$ placas posibles en las que no hay repeticiones de ningún tipo.
Ejemplo. Para guardar información, la memoria principal de una computadora contiene una colección grande de circuitos, cada uno de los cuales es capaz de almacenar un bit. Esto es, alguno de los dígitos binarios (binary digits) $0$ o $1$. Toda la información que se almacena en una computadora consiste de colecciones muy grandes de bits. Por ejemplo, los colores y las imágenes son comúnmente almacenados en forma de arreglos de bits. En el caso de las imágenes, formatos como el PNG (Portable Network Graphics) y el BMP (bitmap, «mapa de bits») son ejemplos de formatos de imagen que consisten de matrices de pequeños cuadraditos de colores llamados pixeles.

Aunado a esto, cada uno de los pixeles tiene un color, el cual es representado a través de un arreglo de bits. Uno de los modelos de color más utilizados en los dispositivos digitales es el modelo RGB (Red Green Blue), que combina los colores primarios rojo, verde y azul para obtener otros colores.
Sin embargo, una computadora tiene acceso a una cantidad limitada de espacios de memoria, por lo que no podemos representar todos los colores visibles. Por ello, hacemos lo posible por representar la mayor cantidad posible de colores con los recursos disponibles para la computadora. Antiguamente, las computadoras y las consolas de videojuegos tenían una cantidad muy limitada de recursos. En consecuencia, dedican una cantidad fija de bits al color. Esta cantidad es conocida como la profundidad de color. Por ejemplo, en la siguiente imagen se muestran todos los colores posibles en una profundidad de color de $6$-bits.

A cada color primario se le dedican $2$ bits, es decir, dos «casillas» en las que puede ir un $0$ o un $1$. Así, en cada «casilla» hay $2$ opciones a escoger, por lo que una cadena de $2$ bits tiene $2 \cdot 2 = 4$ combinaciones posibles de $0$’s o $1$’s.
| Bit 1 | Bit 2 |
|---|---|
| $0$ | $0$ |
| $0$ | $1$ |
| $1$ | $0$ |
| $1$ | $1$ |
En la tabla anterior se ilustran todos los valores que puede tomar la lista de $2$ bits que se asigna a cada color: $00$, $01$, $10$ y $11$. Estos valores pueden pensarse como cifras en sistema binario. Así, $00_{2}$ es $0$, $01_{2}$ es $1$, $10_{2}$ es $2$ y $11_{2}$ es $3$. A cada color primario le corresponde un par de bits que representa la intensidad de rojo, verde y azul que contiene un color compuesto dado. Estos valores se combinan entre sí de manera aditiva. Por ejemplo, tener los valores $01$ en rojo, $00$ en verde y $10$ en azul resulta en un color morado como se muestra en la siguiente figura.

En conclusión, cuando la profundidad de color es de $6$ bits se tiene un total de $(2^2) \cdot (2^2) \cdot (2^2) = 64$ colores disponibles. Para ilustrar lo limitada que resulta esa cantidad, observa la siguiente imagen.

Es por esto que las computadoras y consolas de videojuegos más antiguas tienen ese característico estilo de gráficos pixelados, pues sus capacidades de procesamiento eran tan limitadas que debían de limitar la cantidad de colores que podían presentar en la pantalla o televisión.
Para que te des una idea de cuánto ha avanzado la tecnología, prácticamente cualquier computadora y celular en la actualidad tiene una profunidad de color de $24$ bits, con $8$ bits dedicados a cada color primario. Esto es, se tienen disponibles $(2^8) \cdot (2^8) \cdot (2^8) = 16{,}777{,}216$ colores distintos para escoger.
Tarea moral
Los siguientes ejercicios son opcionales. Es decir, no formarán parte de tu calificación. Sin embargo, te recomiendo resolverlos para que desarrolles tu dominio de los conceptos abordados en esta entrada.
- En una heladería se venden $7$ sabores de helado distintos. A unas cuadras de distancia, hay otra heladería más grande que vende $12$ sabores de helado.
- Asumiendo que los sabores de helado que ofrecen ambas heladerías son todos distintos, ¿cuántos sabores distintos tienes para escoger?
- Si no sabes los sabores que ofrecen ambas heladerías, sea $h$ el número de sabores distintos que se ofrecen en ambas heladerías. ¿Entre qué valores se encuentra $h$?
- Retoma el ejemplo de las placas con $2$ letras y $4$ dígitos.
- Si permitimos repeticiones, ¿cuántas placas tienen únicamente vocales (A, E, I, O, U) y dígitos pares?
- Y si no permitimos repeticiones, ¿cuántas placas tienen únicamente vocales (A, E, I, O, U) y dígitos pares?
- El SNES (Super Nintendo Entertainment System) es una consola muy antigua que posee una profundidad de color de $15$-bits ($5$ bits para cada color primario). ¿Cuántos colores disponibles tiene esta consola?
Más adelante…
En la siguiente entrada abordaremos otras herramientas de conteo, las permutaciones y las combinaciones. Estos nuevos conceptos son resultados que se derivan a partir del principio del producto. Por ello, es recomendable que te quede bien claro este último principio.
Los dos principios vistos en esta entrada son fundamentales para el estudio de la probabilidad clásica. En particular, el principio del producto será de gran utilidad para calcular la cardinalidad de los espacios muestrales de los experimentos aleatorios que veremos en esta parte.
Entradas relacionadas
- Ir a Probabilidad I
- Entrada anterior del curso: El Enfoque Frecuentista
- Siguiente entrada del curso: Principios de Conteo 2 – Permutaciones