Introducción
En la entrada anterior concluimos nuestro estudio de los principios de conteo. Estos principios resultan muy útiles para el cálculo de cardinalidades de conjuntos. Además, la medida de probabilidad que veremos en esta entrada requiere precisamente de cardinalidades de conjuntos para ser calculada. Por ello, los principios de conteo que vimos serán cruciales para el cálculo de probabilidades bajo este enfoque.
Lo que veremos en esta entrada es el enfoque clásico de la probabilidad. A grandes rasgos, este enfoque centra su atención en la cantidad de resultados posibles de un experimento; es decir, la cardinalidad de su espacio muestral. A su vez, dado algún evento de ese espacio muestral, el enfoque clásico establecerá la probabilidad de ese evento es proporcional a su cardinalidad con respecto a la cardinalidad del espacio muestral. Esto significa que bajo el enfoque clásico, el espacio de probabilidad es equiprobable. Veamos qué queremos decir por esto.
Motivación
Ya vimos que en el enfoque frecuentista se propone que la medida de probabilidad debe de representar la «frecuencia relativa» de un evento. Por ello, en la definición de la medida de probabilidad frecuentista de un evento $A$ se toma el límite al infinito de la frecuencia relativa de $A$.
Continuando con nuestro paseo por los enfoques más importantes de la probabilidad, sigue el caso de la probabilidad clásica. En este caso partiremos de un enfoque distinto del frecuentista. Para empezar, motivaremos este enfoque con un ejemplo. Supón que nos interesa modelar el resultado de revolver una baraja inglesa y tomar $4$ cartas, sin reemplazo. Esta actividad se considera un experimento aleatorio pues se revuelve la baraja antes de tomar las $4$ cartas. Podemos representar a una baraja estándar como el conjunto
\begin{align*} \mathfrak{B} = \begin{Bmatrix} \textcolor{red}{\mathrm{A}\heartsuit}, & \textcolor{red}{1\heartsuit}, & \textcolor{red}{2\heartsuit}, & \textcolor{red}{3\heartsuit}, & \textcolor{red}{4\heartsuit}, & \textcolor{red}{5\heartsuit}, & \textcolor{red}{6\heartsuit}, & \textcolor{red}{7\heartsuit}, & \textcolor{red}{8\heartsuit}, & \textcolor{red}{9\heartsuit}, & \textcolor{red}{10\heartsuit}, & \textcolor{red}{\mathrm{J}\heartsuit}, & \textcolor{red}{\mathrm{Q}\heartsuit}, & \textcolor{red}{\mathrm{K}\heartsuit}, \\ \textcolor{red}{\mathrm{A}\blacklozenge}, & \textcolor{red}{1\blacklozenge}, & \textcolor{red}{2\blacklozenge}, & \textcolor{red}{3\blacklozenge}, & \textcolor{red}{4\blacklozenge}, & \textcolor{red}{5\blacklozenge}, & \textcolor{red}{6\blacklozenge}, & \textcolor{red}{7\blacklozenge}, & \textcolor{red}{8\blacklozenge}, & \textcolor{red}{9\blacklozenge}, & \textcolor{red}{10\blacklozenge}, & \textcolor{red}{\mathrm{J}\blacklozenge}, & \textcolor{red}{\mathrm{Q}\blacklozenge}, & \textcolor{red}{\mathrm{K}\blacklozenge}, \\ \mathrm{A}\spadesuit, & 1\spadesuit, & 2\spadesuit, & 3\spadesuit, & 4\spadesuit, & 5\spadesuit, & 6\spadesuit, & 7\spadesuit, & 8\spadesuit, & 9\spadesuit, & 10\spadesuit, & \mathrm{J}\spadesuit, & \mathrm{Q}\spadesuit, & \mathrm{K}\spadesuit, \\ \mathrm{A}\clubsuit, & 1\clubsuit, & 2\clubsuit, & 3\clubsuit, & 4\clubsuit, & 5\clubsuit, & 6\clubsuit, & 7\clubsuit, & 8\clubsuit, & 9\clubsuit, & 10\clubsuit, & \mathrm{J}\clubsuit, & \mathrm{Q}\clubsuit, & \mathrm{K}\clubsuit \end{Bmatrix} \end{align*}
donde cada elemento representa a cada uno de los elementos de la baraja. Por ejemplo, el elemento $\textcolor{red}{9\blacklozenge}$ es el $9$ de diamantes, $\mathrm{Q}\clubsuit$ es la reina de tréboles, $\mathrm{K}\spadesuit$ es el rey de espadas y $\textcolor{red}{\mathrm{J}\heartsuit}$ es la jota de corazones.
¡Atención! El conjunto $\mathfrak{B}$ no es el espacio muestral de nuestro experimento. Recuerda que el espacio muestral de un experimento aleatorio es el conjunto de todos sus posibles resultados. Así, como nuestro experimento consiste en extraer 4 cartas de una baraja revuelta, los elementos del espacio muestral debieran de ser manos de 4 cartas. Además, no importa el orden en el que tomemos las cartas, la mano resultante es la misma.
Por ello, las manos resultantes en este experimento pueden verse como subconjuntos de $\mathfrak{B}$. Por ejemplo, supón que $4$ cartas y te salen $6\clubsuit$, $\textcolor{red}{9\blacklozenge}$, $\mathrm{K}\clubsuit$ y $\textcolor{red}{8\heartsuit}$. El resultado del experimento en esta situación fue ${6\clubsuit, \textcolor{red}{9\blacklozenge}, \mathrm{K}\clubsuit, \textcolor{red}{8\heartsuit}}$, pues en un conjunto no importa el orden. Además, observa que el resultado tiene cardinalidad $4$. En consecuencia, podemos tomar al espacio muestral como
\[ \Omega = \{ M \in \mathscr{P}(\mathfrak{B}) \mid |M| = 4 \}. \]
Es decir, el espacio muestral $\Omega$ de este experimento es el conjunto de todos los subconjuntos de la baraja que tienen $4$ cartas. Como $\mathfrak{B}$ es un conjunto finito (se cumple que $|\mathfrak{B}|=52$), también $\Omega$ es un conjunto finito. De hecho, se cumple que $|\Omega| = {52 \choose 4} = 270{,}725$, pues hay ${52 \choose 4}$ combinaciones de tamaño $4$ de las $52$ cartas. Podemos tomar como σ-álgebra a $\mathscr{P}(\Omega)$, que siempre es un σ-álgebra.
Ahora, ¿qué probabilidad le asignamos a cada evento de $\Omega$? Por ejemplo, ¿cuál es la probabilidad de que en las $4$ cartas que tomamos no haya tréboles? Un posible resultado de este tipo es que las $4$ cartas que nos salgan sean $\{ \textcolor{red}{\mathrm{J}\heartsuit}, 10\spadesuit, \textcolor{red}{9\blacklozenge}, 5\spadesuit \}$. Para hacerlo, el enfoque clásico propone lo siguiente:
La probabilidad de un evento es la proporción entre el número de casos favorables a este, y el número de casos totales del experimento.
Esta hipótesis es conocida como equiprobabilidad. Así, para obtener la probabilidad de que en las $4$ cartas que tomemos no haya tréboles, debemos de obtener cuántas manos de $4$ cartas sin tréboles hay. Para ello, observa que en la baraja hay $13$ cartas que son tréboles. Por tanto, la combinación de cartas de nuestro evento está restringida a las $39$ cartas que no son tréboles. En consecuencia, hay ${39 \choose 4} = 82{,}251$ manos de $4$ cartas sin tréboles, pues hay ${39 \choose 4}$ combinaciones de tamaño $4$ de las $39$ cartas que no son tréboles. Así, desde el enfoque clásico de la probabilidad, la probabilidad de que en las $4$ cartas que tomemos no haya tréboles es
\[ \frac{\text{Número de casos favorables}}{\text{Número de casos totales}} = \frac{{39 \choose 4}}{{52 \choose 4}} = \frac{82{,}251}{270{,}725} \]
Definición de una medida equiprobable
De acuerdo con la motivación expuesta en la sección anterior, presentamos la definición formal de un espacio equiprobable. Esta definición resume las ideas del enfoque clásico de la probabilidad.
Definición. Sea $\Omega$ un conjunto finito. Definimos a $\mathbb{P}\colon \mathscr{P}(\Omega) \rightarrow \mathbb{R}$, la medida de probabilidad clásica, como sigue. Para cada $A \in \mathscr{P}(\Omega)$, se define la probabilidad de $A$ como
\[ \Prob{A} = \frac{|A|}{|\Omega|}. \]
Un espacio de probabilidad $(\Omega, \mathscr{F}, \mathbb{P})$ con esta medida de probabilidad es conocido como un espacio equiprobable.
De acuerdo con la definición anterior, el enfoque clásico de la probabilidad tiene dos hipótesis importantes sobre el fenómeno aleatorio que se intenta describir:
- Primero, que $\Omega$ el espacio muestral del fenómeno es finito.
- Segundo, que se trata de un espacio equiprobable. Esto es, que si el fenómeno tiene $|\Omega|$ resultados posibles, entonces cada uno tiene una probabilidad de ocurrencia igual a $\frac{1}{|\Omega|}$.
En particular, el segundo supuesto puede ser problemático. ¿Qué nos asegura que al revolver la baraja del último ejemplo obtenemos efectivamente un espacio equiprobable? Hay que tener cuidado con esto, ya que es un supuesto muy fuerte que no necesariamente se cumple.
Importante. En la literatura referente a la probabilidad, es común encontrar la expresión «al azar» en la forma de «se escoge un estudiante del grupo al azar», o «se escoge(n) una(s) carta(s) de la baraja al azar». Sin embargo, no existe una manera única de hacer una tarea «al azar», ya que hay muchísimas medidas de probabilidad, así que podría resultar ambiguo. Por ello, es común que la expresión «al azar» se refiera a asumir que el espacio es equiprobable, a menos que se indique lo contraro.
Ejemplos con el enfoque clásico
Ejemplo 1. En una encuesta a 120 comensales, un restaurante encontró que \(48\) personas consumen vino con sus alimentos, \(78\) consumen refresco, y \(66\) consumen té helado. Además, se encontró que \(36\) personas consumieron cada par de bebidas con sus alimentos. Es decir, \(36\) personas consumieron vino y refresco; \(36\) consumieron vino y té helado; etcétera. Finalmente, el último hallazgo fue que \(24\) personas consumieron todas las bebidas.
Si se eligen \(2\) comensales al azar, de manera equiprobable, de este grupo de \(120\), cuál es la probabilidad de que
- ambos quieran únicamente té helado con sus alimentos? (Evento \(A\))
- ambos consuman exactamente dos de las tres opciones de bebidas? (Evento \(B\))
Utilizando la información provista por la encuesta, podemos construir el siguiente diagrama de Venn-Euler:
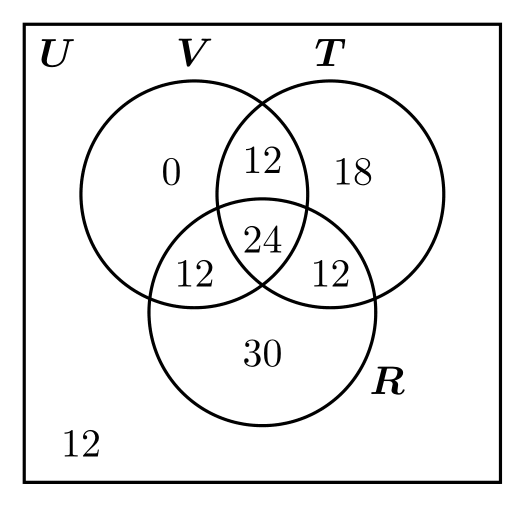
Sin embargo, nota que nuestro espacio muestral no es \(U\), porque lo que hacemos es tomar dos personas al azar. Por ello, el espacio muestral \(\Omega\) consiste de todos los pares de comensales que se pueden elegir de la muestra de \(120\). Por ello, \(|\Omega| = \binom{120}{2} = 7140\). Por otro lado, el diagrama nos dice que hay \(18\) comensales que consumieron únicamente té helado con sus alimentos. Por ello, el número de pares de comensales que consumieron únicamente té helado es \(\binom{18}{2}\). Esto quiere decir que \(|A| = \binom{18}{2} = 153\). En consecuencia,
\begin{align*} \Prob{A} &= \frac{|A|}{|\Omega|} = \frac{153}{7140} \approx 0.02143. \end{align*}
Esto es, la probabilidad de que las dos personas escogidas consuman únicamente té helado es aproximadamente \(2.143\%\).
Ejemplo 2. Sea \(X = \{1,2,3,\ldots,99,100\}\). Imagina que seleccionamos \(2\) elementos de \(X\) al azar, sin reemplazo. ¿Cuál será la probabilidad de que la suma de esos dos números sea par?
Para encontrar esta probabilidad, primero hay que plantear nuestro espacio muestral y el evento cuya probabilidad queremos. Lo que hacemos es seleccionar \(2\) elementos de \(X\) sin reemplazo, así que nuestro espacio muestral \(\Omega\) debe de tener pares de números. Sin embargo, nota que son pares en los que no importa el orden, pues elegir los números \(14\) y \(73\) es lo mismo que escoger los números \(73\) y \(14\). Por ello, \(\Omega\) es el conjunto de subconjuntos de \(X\) que tienen exactamente dos elementos. Esto es,
\begin{align*} \Omega &= \{ A \in \mathscr{P}(X) \mid |A| = 2 \}. \end{align*}
En consecuencia, tenemos que \(|\Omega| = \binom{100}{2} = 4950\). Ahora, queremos la probabilidad del evento de que la suma de los \(2\) números escogidos sea par. Es decir, buscamos la probabilidad de \mathcal{B} definido como
\begin{align*} \mathcal{B} &= \{ \{a, b\} \in \Omega \mid \text{\(a + b\) es par} \}. \end{align*}
Sin embargo, no parece haber una forma inmediata de calcular \(|\mathcal{B}|\), con lo que podríamos calcular \(\Prob{\mathcal{B}}\). No obstante, podemos descomponer a \(|\mathcal{B}|\) en dos conjuntos cuya cardinalidad sí es posible calcular. Para ello, observa que los elementos de \(X\) pueden ser pares o impares, sin otra opción. En consecuencia, hay \(3\) casos posibles al elegir \(2\) elementos de \(X\). Sea \(A = \{a, b\} \in \Omega\). Entonces puede pasar que
- \(a\) y \(b\) son ambos pares. Es decir, existen \(p, q \in \mathbb{Z}\) tales que \(a = 2p\) y \(b = 2q\). En consecuencia, \(a + b = 2p + 2q = 2(p + q)\). En conclusión, si \(a\) y \(b\) son pares, entonces \(a + b\) es par.
- \(a\) es par y \(b\) es impar (y viceversa). En este caso, existen \(p, q \in \mathbb{Z}\) tales que \(a = 2p\) y \(b = 2q + 1\). Por ello, \(a + b = 2p + 2q + 1 = 2(p+q) + 1\). Por lo tanto, si \(a\) es par y \(b\) es impar, entonces \(a + b\) es impar.
- \(a\) y \(b\) son impares. Esto implica que existen \(p, q \in \mathbb{Z}\) tales que \(a = 2p + 1\) y \(b = 2q + 1\). Por tanto, \(a + b = 2p + 1 + 2q + 1 = 2(p+q+ 1)\). Así, si \(a\) y \(b\) son impares, entonces \(a+b\) es impar.
De este modo, tenemos que \(\mathcal{B}\) se puede descomponer en la unión de dos eventos:
- \(\mathcal{E}_{1}\) : El evento de que los dos números escogidos sean pares:\begin{align*}\mathcal{E}_{1} = \{\{a, b\} \in \Omega \mid \text{\(a, b\) son pares}\}.\end{align*}
- \(\mathcal{E}_{2}\) : El evento de que los dos números escogidos sean impares:\begin{align*}\mathcal{E}_{2} = \{\{a, b\} \in \Omega \mid \text{\(a, b\) son impares}\}.\end{align*}
Como en \(X\) hay \(50\) pares y \(50\) impares, se tiene que \(|\mathcal{E}_{1}| = |\mathcal{E}_{2}| = \binom{50}{2} = 1225\). Además, observa que \(\mathcal{E}_{1} \cup \mathcal{E}_{2} = \mathcal{B}\), y que además son eventos ajenos. En consecuencia,
\begin{align*}|\mathcal{B}| &= | \mathcal{E}_{1} \cup \mathcal{E}_{2} | = | \mathcal{E}_{1} | + | \mathcal{E}_{2} | = \binom{50}{2} + \binom{50}{2} = 2450.\end{align*}
Finalmente, con esta información podemos calcular \(\Prob{\mathcal{B}}\). En efecto,
\begin{align*} \Prob{ \mathcal{B}} &= \frac{|\mathcal{B}|}{|\Omega|} = \frac{2450}{4950} = \frac{49}{99} = 0.4949494949\ldots \end{align*}
Un consejo: En los problemas donde se utiliza la probabilidad clásica (es decir, se asume equiprobabilidad en un espacio finito), es recomendable que dejes el cálculo de las probabilidades hasta el final. Realmente el meollo de estos problemas es contar la cantidad de resultados que tiene el espacio muestral \(\Omega\), así como el número de resultados que tiene un evento \(A\). Por ello, centra tu atención en esos cálculos antes de calcular probabilidades.
Tarea moral
Los siguientes ejercicios son opcionales. Es decir, no formarán parte de tu calificación. Sin embargo, te recomiendo resolverlos para que desarrolles tu dominio de los conceptos abordados en esta entrada.
- Demuestra que la medida de probabilidad clásica es una medida de probabilidad.
- En el ejemplo de la encuesta a los comensales, verifica que
- los números en el diagrama de Venn-Euler son las cardinalidades correctas.
- la probabilidad del evento \(B\) es \(3/34 \approx 0.08824\).
- Usando el conjunto \(X = \{1,2,\ldots,99,100\}\) del Ejemplo 2, si se eligen 3 elementos de \(X\) al azar y sin reemplazo, ¿cuál es la probabilidad de que la suma de estos 3 números sea par? Sugerencia: Procede de manera similar a como hicimos aquí, y obtén los casos en los que la suma de los \(3\) números resulta en un número par.
Más adelante…
Esta entrada concluye nuestro estudio de los tres enfoques que contempla el temario de la Facultad de Ciencias para Probabilidad I. Es importante entender que los enfoques (o interpretaciones) de la probabilidad que hemos visto tienen gran importancia histórica. Sin embargo, pueden ser escritos matemáticamente a través de las herramientas que construimos al principio, que conforman el enfoque más moderno de este curso: la probabilidad axiomática. Es conocida de esta manera pues se parte de ciertos objetos matemáticos que satisfacen ciertas reglas (conocidas como axiomas). Este enfoque axiomático, que rige sobre el contenido de estas notas, se atribuye al matemático ruso Andrey Nikolaevich Kolmogorov. Además, es un enfoque flexible que nos ha permitido revisar los enfoques históricos de la probabilidad como casos particulares dentro de la teoría que hemos desarrollado.
Si te interesa saber más sobre la historia de la probabilidad, el libro Introducción a la Teoría de la Probabilidad, Vol. I, del Dr. Miguel Ángel García Álvarez tiene una sección no muy larga dedicada al panorama histórico de esta rama de las matemáticas. Además, al final de esta sección incluye varias referencias de matemáticos de suma importancia en el desarrollo de la probabilidad, como Bernoulli y Laplace, o el mismo Kolmogorov.
Entradas relacionadas
- Ir a Probabilidad I
- Entrada anterior del curso: Principios de Conteo 3 – Combinaciones
- Siguiente entrada del curso: Probabilidad Condicional






