Introducción

En la geometría elemental se tienen varias construcciones realizadas con únicamente regla y compas, esto nos parecerá algo limitante, pero es así como Platón lo plantea para la geometría. Pero son estas restricciones lo que hace interesante las construcciones, cabe aclarar que cuando se menciona regla es para únicamente trazar rectas sin distancia fija, y el compás para trazar circunferencias únicamente. Son estas limitaciones las que hacen que muchas construcciones no se puedan realizar, es en este punto donde hablaremos de ‘Los tres problemas famosos griegos’ los cuales son: La trisección del ángulo, la duplicación del cubo y la cuadratura del círculo.

Este grupo de problemas imposibles enunciados en el siglo V a.C. y hasta la demostración de que la solución es imposible en el siglo XIX, generaron que grandes matemáticos pensaran en su solución, así mismo se motivó al desarrollo de diversas áreas de las matemáticas. Como se mencionó, las restricciones de únicamente regla y compas son las que imposibilitan la solución, pero si se modificaran estas restricciones adecuadamente, estos problemas pueden ser resueltos. Es por ello que se mostrara la imposibilidad de resolver los tres problemas famosos.

Trisección del ángulo

Problema. Lograr trisecar un ángulo arbitrario con regla y compas. Se mostrará la imposibilidad de resolver este problema.

Demostración. Dado un ángulo, no siempre es posible construir solo con una regla y compas un ángulo cuya medida es un tercio del ángulo original.
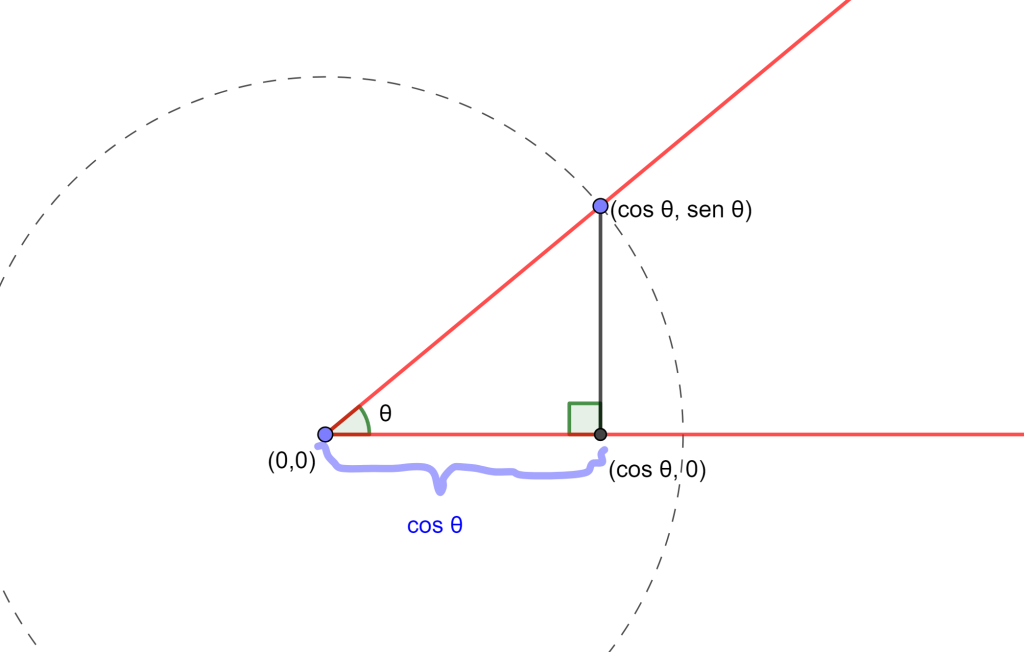
Tenemos que mostrar lo que significa construir un ángulo a números construibles, ya que un número construible es la longitud de un segmento, no una medida de un ángulo. Recordemos que si tenemos algún ángulo construido sin perdida de generalidad, se asume que este ángulo está en la posición estándar, de modo que su lado inicial este en el eje $x$ positivo.

Se puede asignar el vértice del ángulo con el origen de nuestro plano y luego construir un círculo unitario centrado en el origen, donde tendremos un punto de intersección que por trigonometría este punto es ( $cos \theta, sen \theta $ ) y si tomamos la perpendicular de este punto hasta el eje $x$, nos dara un punto ( $cos \theta , 0 $ ) y por lo cual se tiene la distancia $cos \theta$.

Entonces si el angulo theta $\theta$ es construible eso significa que la distancia $cos \theta $ es construible y este proceso es reversible, por lo que podemos construir el ángulo theta $\theta$ si y solo si podemos construir el coseno de distancia de theta $\theta$. Por lo cual se querrá argumentar que el coseno de theta ($cos \theta$) no es un número construible para todos los theta $\theta$.

Tenemos la siguiente identidad trigonométrica

$cos 3\theta = 4 cos^3 \theta – 3 cos \theta.$

Es importante recalcar que queremos $cos 3 \theta$, porque queremos ángulos de trisección. Si tomamos $\theta = 20^o $, entonces ingresándolo en la fórmula se tiene

$cos 3\theta = cos (3)(20^o)=cos 60^o= 1/2.$

Si definimos $\alpha=cos \theta$ entonces se tiene que la igualdad queda

$4\alpha ^3 – 3 \alpha = 1/2.$

Multiplicamos por 2 en ambos lados

$8 \alpha ^3 – 6\alpha = 1$

$8\alpha ^3 – 6 \alpha -1 =0.$

Entonces $\alpha $ es una raíz del polinomio

$8x^3-6x-1.$

Este es un polinomio de grado 3 si es irreducible, eso sucede si y solo si no tiene raíces, porque si es irreducible tiene un factor lineal, y si tiene un factor lineal tiene una raíz por el teorema de las raíces racionales, las únicas raíces racionales posibles de este polinomio son

$\pm 1, \pm 1/2, \pm 1/4, \pm 1/8.$

Ninguno de estos ocho números son raíces de este polinomio, este polinomio por lo cual es irreducible porque no tiene raíces racionales, por lo tanto, este polinomio debe sé el polinomio mínimo para el coseno de $20^o$.
Ahora, ya que este es un polinomio de grado 3, si tomamos el conjunto de los racionales $\alpha$ y vemos su grado sobre $\mathbb{Q}$ tenemos 3.

$[ \mathbb{Q} (\alpha) : \mathbb{Q} ] = 3.$

Pero una propiedad de los números construibles dice que

$[ \mathbb{Q} (\alpha) : \mathbb{Q} ] = 2^n.$

Esto es una potencia de 2, pero 3 no es potencia de 2, $3\neq 2^n.$

Por lo tanto, esto no puede ser una extensión construible, por lo cual el $cos 20^o$ no es un número construible, entonces un ángulo de $20^o$ no se puede construir y un ángulo de $60^o$ no se puede trisecar usando solo regla y compas.

$\square$

Duplicación del cubo

Problema. Se demostrará que la duplicación del cubo es imposible.
Duplicar el cubo nos dice que dada la arista de un cubo, es imposible construir con una regla y compas el borde de un cubo que tiene el doble del volumen del cubo original.

Demostración. Imaginemos el cubo con la longitud de un lado de $S$ y este es un número construible, el volumen de este cubo sería $V=S^3$; Por lo cual si tuviéramos que construir un cubo cuyo volumen sea el doble, entonces el volumen sería $V=2S^3$ este cubo es más grande, y nos preguntaremos cuanto deben medir los lados de este nuevo cubo.

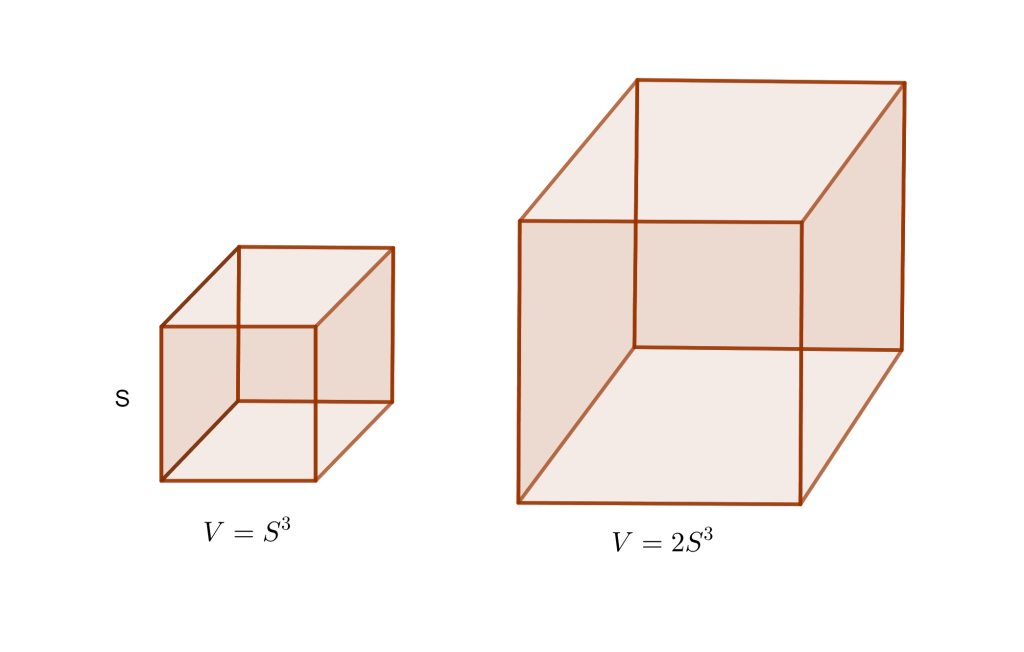
Entonces el cubo duplicado, su volumen debe ser $2S^3$, y sea la longitud de lado $t$, entonces el $V=t^3=2S^3$, despejando $t$ se tiene

$t=\sqrt[3]{2S^3}=\sqrt[3]{2}S.$

Ahora el cuerpo de números construibles es un campo, si podemos construir $S$, entonces podemos dividir por $S$, pero $\sqrt[3]{2}$ no es número construible, ya que

$[ \mathbb{Q} (\sqrt[3]{2}) : \mathbb{Q} ] = 3.$

Pero una propiedad de los números construibles dice que ($\alpha$ es un número construible)

$[ \mathbb{Q} (\alpha) : \mathbb{Q} ] = 2^n.$

Pero $3\neq 2^n$, entonces $\sqrt[3]{2}$ no se puede construir y, por lo tanto, no podemos duplicar el cubo.

$\square$

Cuadratura del círculo

Problema. Por demostrar la imposibilidad de la construcción geométrica clásica de cuadrar el círculo.

Demostración. Dado un círculo de diámetro construible, no siempre es posible construir solo con una regla y compas el borde de un cuadrado que tiene la misma área que el círculo original.
El contraejemplo será que, se tome el círculo unitario, con radio $r=1$ número construible, el área es $A=\pi r^2 = \pi$.

Se debe mostrar que no se puede construir un cuadrado cuya área sea $\pi$ y recordemos que si tenemos un cuadrado con lado $S$ y el área es $A=S^2$. Ahora, si $\pi$ fuera igual a $S^2$ ($\pi = S^2$), esto nos diría que si tomas la raíz cuadrada de ambos lados se tiene $\sqrt{\pi}= S.$

Entonces se requiere construir un lado de longitud $\sqrt{\pi}$.
Pero si $\sqrt{\pi}$ fuera construible, entonces si elevamos al cuadrado $\sqrt{\pi}^2 = \pi$ y el campo de números construibles es un campo, por lo cual $\sqrt{\pi}^2$ también es construible, pero $\pi$ es un número trascendental y ninguna extensión algebraica de $\mathbb{Q}$ contiene $\pi$. El campo de números construibles es una extensión algebraica infinita de los números racionales y, por lo tanto, no contiene números trascendentales, y de ahí se tiene la contradicción $pi$ no es un número construible.
Por lo tanto, es imposible construir un cuadrado para cada círculo.

$\square$

Más adelante…

Se verá el Teorema de Stewart.

Entradas relacionadas

• Ir a Geometría Moderna II
• Entrada anterior del curso: Construcciones con regla o compas
• Siguiente entrada del curso: Teorema de Stewart

Introducción

A partir de la involución en una hilera de puntos y sus puntos conjugados relacionados con la razón cruzada, es que nace el concepto de haces de líneas en involución. Muchos de los resultados que se muestran son gracias al principio de dualidad.

Haces de líneas en involución

Definición. Dado un haz de rectas correlacionadas por parejas y donde los puntos de intersección de los pares con cualquier transversal que no pase por el vértice del haz son pares conjugados de una involución de puntos.

Ejemplo: Sean el haz con las rectas correlacionadas por pares $a,a’,b,b’,c$ y $ c’$. Tracemos una recta que corte al haz de rectas y que no pase por $O’$, se tienen las intersecciones $A,A’,B,B’,C$ y $C’$ y donde estos son pares de puntos conjugados de una involución. De esta forma se tiene un haz de rectas en involución.

$\triangle$

Propiedades

$\triangle$

Haz en involución y el vértice en la circunferencia

Teorema. Sea un haz de rectas en involución donde se tienen los pares conjugados $a,a’,b,b’,c,c’$ y que tienen su vértice en una circunferencia, y si estas rectas cortan la circunferencia nuevamente en $A,A’,B,B’,C,C’$ respectivamente, entonces las rectas $AA’, BB’, CC’$ son concurrentes.

Demostración. Tracemos una recta $l$ que corte al haz y no pase por $Q$, nos da las intersecciones $A_1, B_1, C_1, A_1′, B_1′, C_1’$.

Como los haces de líneas está en involución y cualquier recta que corte al haz nos da una hilera de puntos en involución, por el teorema de razón cruzada con hilera de puntos nos da la siguiente igualdad.

$\{A_1A_1’B_1C_1\}=\{A_1’A_1B_1’C_1’\}$

Por propiedades de razón cruzada se cumple:

$\{aa’bc\}=\{a’ab’c’\}$

Se puede decir que la propiedad de razón cruzada también se cumple para haz de rectas en involución, es decir, que cualesquiera cuatro rectas que tiene de esa involución la razón cruzada va a ser a la de sus correspondientes.
Observemos que estos haces salen a partir del punto $Q$ y pasan por los puntos de intersección con la circunferencia. Entonces se puede poner el haz desde $Q$:

$Q\{AA’BC\}=Q\{A’AB’C’\}$

Y va a ser lo mismo si cambiamos $Q$ por $B’$ y $C$:

$B’\{AA’BC\}=C\{A’AB’C’\}$

Tracemos las rectas $AA’$, $BB’$ y $CC’$, y tracemos la recta $B’C$, donde se tienen las intersecciones con $AA’$ que son $X,Y $ y $Z$. Por demostrar que $X=Y$.

La razón cruzada de $B’\{AA’BC\}=B’\{AA’XZ\}$ y, por otro lado, $C\{A’AB’C’\}=C\{A’AZY\}$, entonces $\{AA’XZ\}=\{A’AZY\}$. De esta igualdad se tienen tres puntos iguales $A’,A$ y $Z$, y el cuarto punto $X$ y $Y$ deben ser iguales, ya que si intercambiamos dos puntos de esta razón cruzada, los otros dos también deben intercambiarse, para que se conserve la razón cruzada entonces se tiene la igualdad:

$\{AA’XZ\}=\{AA’YZ\}$

Por lo cual $X=Y$ y se concluye que las rectas $AA’$, $BB’$ y $CC’$ son concurrentes.

$\square$

Del resultado anterior se puede generar la duda de que pasa si la involución es hiperbólica o elíptica, por ende se debe definir de manera más formal.

Definición. Sea $a,a’,b,b’,c,c’$ los haces de líneas en involución y una recta $l$ que no pase por el vértice $Q$ del haz, la cual generara intersecciones con el haz, las cuales son $A,A’,B,B’,C,C’$ respectivamente.

• Si $A,A’,B,B’,C,C’$ es una involución elíptica, se dice que el haz está en involución elíptica.
• Si $A,A’,B,B’,C,C’$ es una involución hiperbólica, se dice que el haz está en involución hiperbólica.

Rectas Conjugadas en ángulos rectos

Teorema. En un haz de rectas en involución siempre hay un par de rectas conjugadas perpendiculares entre sí, por otra parte, si existe más de un par de rectas conjugadas en ángulos rectos, entonces todos los pares conjugados son perpendiculares entre sí y la involución es elíptica.

Demostración. Sea un haz de rectas en involución $a,a’,b,b’,c,c’$ con $Q$ vértice, tracemos una circunferencia con centro $O$ que pase por $Q$ y el haz corte a la circunferencia en los puntos $A,A’,B,B’,C,C’$ respectivamente al orden que se mencionó las rectas.
Por el teorema anterior se afirma que las rectas $AA’, BB’, CC’$ son concurrentes en $X$. Tracemos la recta $XO$, la cual corta a la circunferencia en dos puntos $D$ y $D’$ los cuales son puntos extremos del diámetro $DD’$. Si trazamos las rectas $DQ$ y $D’Q$ nos forma un ángulo recto $\angle DQD’$.

Por demostrar que las rectas $DQ$ y $D’Q$ son un par conjugado de la involución. Tracemos una recta $l$ que corte al haz $a,a’,b,b’,c,c’$ en involución en los puntos $A_1,A_1′,B_1,B_1′,C_1,C_1’$ respectivamente, además corta a las rectas $QD$ y $QD’$ en $D_1$ y $D_1’$ respectivamente.

Tenemos que ver que los pares $D_1$ y $D_1’$ están en la hilera de puntos en involución, entonces supongamos que $D_1$ tiene su par conjugado en la involución $D_1’$$’$, se quiere demostrar que $D_1’=D_1’$$’$. Por teorema de razón cruzada en involución se tienen las siguientes igualdades:

$\{A_1B_1C_1D_1\}=\{A_1’B_1’C_1’D_1’$$’\}$ y $\{A_1B_1C_1D_1\}=Q\{ABCD\}$.

Ahora en razón cruzada nos dice que si cuatro secantes que pasan por un punto $X$ y al observar la razón cruzada del haz formado por un punto $Q$ en la circunferencia con los puntos $A,B,C,D$ debe ser la misma razón cruzada del haz con los puntos correspondientes de la secante ósea $A’,B’,C’,D’$, lo cual da la igualdad:

$Q\{ABCD\}=Q\{A’B’C’D’\}$ y ademas $Q\{A’B’C’D’\}=\{A_1’B_1’C_1’D_1’\}$.

Por lo cual da la igualdad:

$\{A_1’B_1’C_1’D_1’$$’\}=\{A_1B_1C_1D_1\}=Q\{ABCD\}=Q\{A’B’C’D’\}=\{A_1’B_1’C_1’D_1’\}$

Entonces $\{A_1’B_1’C_1’D_1’$$’\}=\{A_1’B_1’C_1’D_1’\}$ por ende $D_1’=D_1’$$’$, se concluye que $DQ$ y $D’Q$ son un par conjugado perpendicular de la involución.

Ahora, si existe otro par de rectas conjugadas en ángulos rectos, las cuales supongamos que son $b$ y $b’$, esto nos diría que sus puntos $B$ y $B’$ son diametralmente opuestos, por lo cual, las rectas $DD’$ y $BB’$ se cortan en el centro $O$.
Y como se tiene el haz de rectas conjugadas en involución $a,a’,DQ,D’Q, b,b’$ entonces las rectas $AA’,DD’$ y $BB’$ son concurrentes, pero como $DD’$ y $BB’$ se cortan en $O$ entonces también $AA’$ pasa por $O$. Se concluye que todos los pares conjugados son perpendiculares entre sí y la involución es elíptica.

$\square$

Teoremas relacionados con los haces de líneas en involución

Se mencionarán tres teoremas, los cuales se dejaran como ejercicios a resolver.

Teorema. Dado un cuadrángulo completo, sus tres pares de lados opuestos son intersecados por cualquier transversal que no pasa por un vértice en tres pares de puntos conjugados de una involución.

Teorema. Sea un cuadrángulo inscrito en una circunferencia, cualquier recta que no pase por un vértice, corta a la circunferencia y los pares de lados opuestos del cuadrángulo en una involución.

Teorema. Si dos pares de lados opuestos de un cuadrángulo completo son ortogonales, el tercer par es también ortogonal.

Más adelante…

Se dejarán los ejercicios correspondientes a esta unidad de Razón Cruzada.

Entradas relacionadas

• Ir a Geometría Moderna II
• Entrada anterior del curso: Hileras de puntos en involución
• Siguiente entrada del curso: Ejercicios Unidad 4

Introducción

Tres teoremas importantes en la razón cruzada son el Teorema de Pascal, Brianchon y Pappus. Con estos se muestran propiedades de colinealidad y concurrencia.

Teorema de Pascal

Teorema. Sea un hexágono inscrito en una circunferencia, los puntos de intersección de sus lados opuestos son colineales.

Demostración. Sea el hexágono inscrito $ABCDEF$ en la circunferencia $O$, donde sus lados opuestos $AB,DE$, $BC,EF$ y $CD,FA$ se intersecan en los puntos $P,Q$ y $R$ son colineales. Ahora $FA$ interseca a $DE$ en $H$ y $EF$ interseca a $CD$ en $K$.

Por propiedades de razón cruzada en la circunferencia se tiene $A\{EDBF\}=C\{EDBF\}$ y por lo cual $\{EDPH\}=\{EKQF\}$, como se observa en la siguiente imagen.

Así mismo se tiene que al unir $R$ con estos puntos se cumple la propiedad $R\{EDPH\}=R\{EKQF\}$. Donde $RE$ coincide con $RE$, $RD$ coincide con $RK$ y $RH$ coincide con $RF$, por ende estos dos haces coinciden en la primera, segunda y cuarta recta, y al tener 3 rectas y una constante distinta de -1, es posible construir una única cuarta recta tal que la razón cruzada sea la constante elegida por ello $RP$ coincide con $RQ$. Y, por lo tanto, $PQR$ son colineales y a esta es la línea de Pascal del hexágono.

$\square$

Teorema de Brianchon

Este es un teorema dual al de Pascal, el cual es aplicable a hexágonos circunscritos a cualquier sección cónica. En nuestro caso se mostrará para una circunferencia.

Teorema. Sea un hexágono circunscrito a una circunferencia, entonces las líneas que unen sus vértices opuestos son concurrentes.

Demostración. Sea el hexágono $ABCDEF$ circunscrito a la circunferencia $O$, ahora los puntos de tangencia de los lados del hexágono $ABCDEF$ son los vértices del hexágono $A’B’C’D’E’F’$.

Si observamos los lados opuestos del hexágono $A’B’C’D’E’F’$ estos se intersecan de la siguiente forma:

Por propiedad de los Polos y Polares, las polares de $A$ y $D$ pasan por $P$ y la polar de $P$ es $AD$. De igual forma, la polar de $Q$ es $BE$ y la polar de $R$ es $CF$, y por el Teorema de Pascal el hexágono inscrito $A’B’C’D’E’F’$ los puntos de intersección de sus lados opuestos $P$, $Q$ y $R$ son colineales, y por lo cual sus polares $AD$, $BE$ y $CF$ son concurrentes y a este es el punto de Brianchon.

$\square$

Teorema de Pappus

Teorema. Si los vértices de un hexágono están alternativamente en dos líneas rectas, entonces la intersección de los pares de lados opuestos genera puntos los cuales son colineales.

Demostración. Este es un caso especial del Teorema de Pascal para un hexágono inscrito en una sección cónica. Sea el hexágono $ABCDEF$, donde la intersección de los lados opuestos son:

Se tiene que $AF$ interseca a $ED$ en $H$, y $EF$ interseca a $CD$ en $K$.

Por lo cual $A\{EBDF\}$ es igual a $C\{EBDF\}$, entonces $\{EPDH\}=\{EQKF\}$.

Uniendo $RQ$ los cuatro puntos de las líneas $ED$ y $EF$, se tiene que $R\{EPDH\}=R\{EQKF\}$.
Ahora como $RE$ coincide con $RE$, $RD$ coincide con $RK$ y $RH$ coincide con $RF$, entonces $RP$ y $RQ$ coinciden, por lo tanto, $P$, $Q$ y $R$ son colineales.

$\square$

Más adelante…

Otro tema interesante por abordar es la involución tanto en Hileras de puntos como Haces de líneas.

Entradas relacionadas

• Ir a Geometría Moderna II
• Entrada anterior del curso: Puntos autocorrespondientes y regla geométrica de la falsa posición
• Siguiente entrada del curso: Hileras de puntos en involución