Introducción

Esta entrada es parte de una serie de notas introductorias sobre técnicas de demostración. En esta entrada se habla sobre demostraciones de proposiciones con cuantificadores. Cada entrada está ligeramente relacionada con las otras. Para entenderlas bien, usamos el siguiente diagrama que recopila cómo se comporta un mundo fantástico llamado Axios, en donde habitan creaturas llamadas Blorgs. Para leer más sobre ello, haz click aquí.

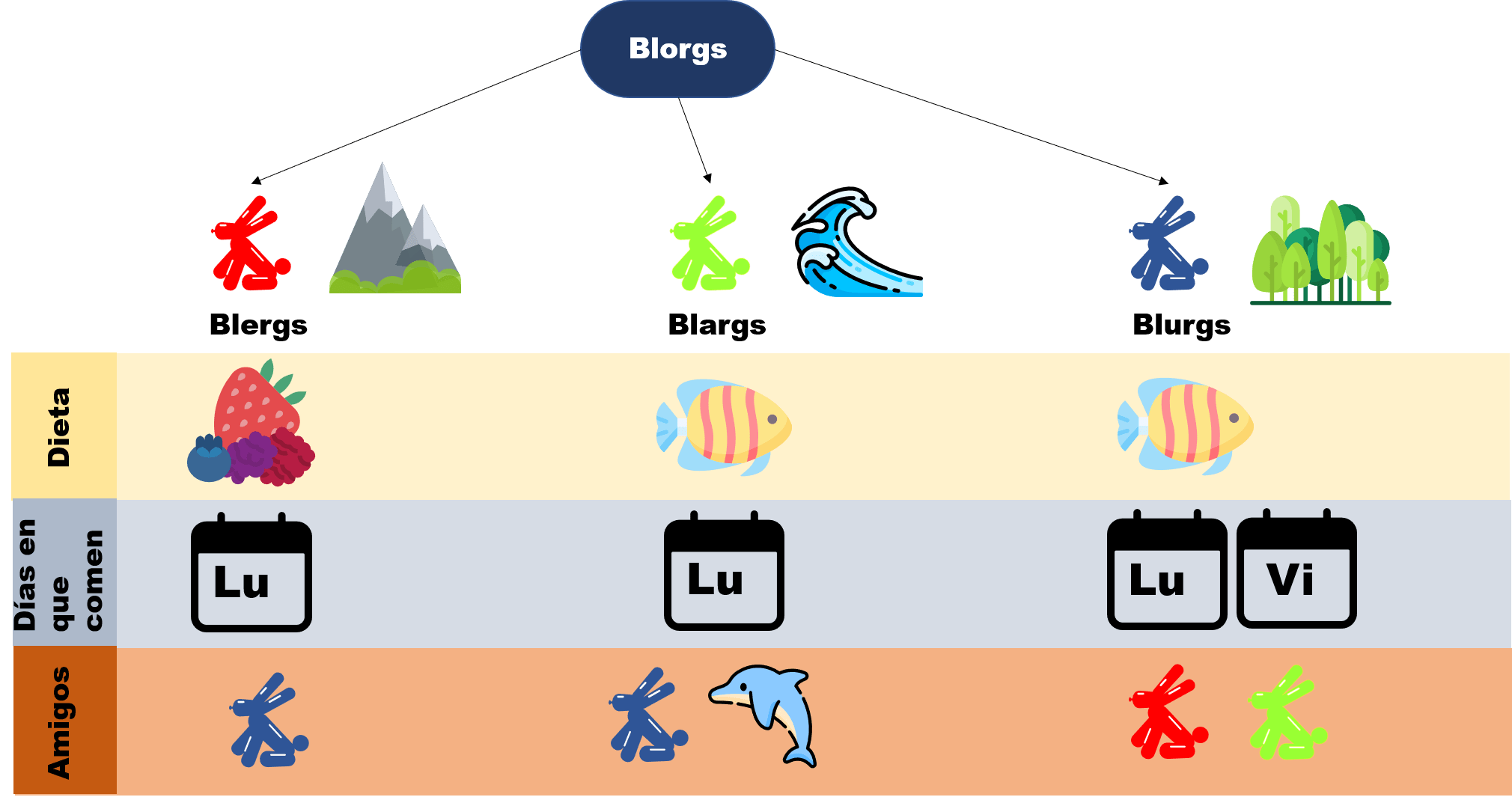
En esta entrada revisaremos más a fondo cómo es que los cuantificadores que repasamos antes se usan dentro de las proposiciones y cómo demostrar estas. Veremos ejemplos con cuantificadores universales y existenciales, y algunos ejemplos famosos de proposiciones que los usan.

Los cuantificadores en las demostraciones

Ya hemos trabajado antes con los cuantificadores, aunque quizás no lo hayas notado. Por ejemplo, cuando hicimos la demostración de «Los Blorgs verdes comen peces», lo que hicimos fue considerar cualquier Blorg verde e hicimos una serie de pasos lógicos para demostrarlo. En ningún lugar dice que sólo algunos Blorgs verdes comen peces, en general dice que los Blorgs verdes comen peces, es decir todos los Blorgs verdes cumplen la condición de comer peces. ¿La palabra resaltada te recuerda algo? Seguramente a lo que vimos en la entrada de cuantificadores.

Como recordatorio, para usar cuantificadores necesitamos un universo de discurso y un predicado $P(x)$, que podíamos pensar como una proposición en donde aún no decidimos quién es $x$ de entre los objetos de nuestro universo de discurso. Considerando como universo de discurso a los Blorgs, podemos tomar el predicado $P(x) = \text{$x$ come los viernes}$. Sería falso entonces afirmar que

$$\forall x: P(x),$$

pues los únicos que comen los viernes son los Blurgs. En cambio existe al menos una especie que sí come esos días, así que sería verdadero decir:

$$\exists x: P(x), $$

ya que al tomar un Blurg $x$, tendríamos que $P(x)$ es verdadero y por lo tanto la proposición cuantificada $\exists x: P(x)$ también.

Así que podríamos demostrar la siguiente afirmación:

Proposición. Existen Blorgs que comen los viernes.

Demostración. Para ello, notemos que un Blorg puede ser Blarg, Blerg y Blurgs. A continuación vamos a considerar a $x$ un Blorg que es Blurg. Y como sabemos, todos los Blurgs comen los lunes y viernes. En particular, comen los viernes, por lo que hemos demostrado la proposición.

$\square$

Diferencias entre cuantificadores

Vamos a detenernos y analizar cómo se diferenció la última demostración con lo que hemos estado haciendo antes. Analiza la demostración anterior con la siguiente:

Proposición. Los Blorgs comen un día antes de los Martes.

Demostración. Consideremos $x$ un blorg. Como es un blorg puede que sea un blarg, blerg o blurg.

Caso 1. $x$ es un Blarg.

Como $x$ es Blarg, entonces come los Lunes, que resulta ser un día antes de los Martes.

Caso 2. $x$ es un Blerg.

Igual que en el caso anterior, si $x$ es Blerg, entonces come los días antes de los Martes.

Caso 3. $x$ es un Blurg.

Sabemos que los Blurgs comen los Lunes y los Viernes. Si $x$ es un Blurg, entonces en particular come los lunes, y así, come los días antes de los Martes.

En cualquiera de los casos, $x$ cumple la proposición.

$\square$

Esta es una demostración que bien pudimos haber escrito como «Todos los Blorgs comen los días antes de los Martes». Sin embargo, en la práctica no es muy común ver escrito explícitamente la palabra «todos/todas», pues al hablar de «Los Blorgs», se infiere que hablamos de todos los Blorgs. Así podemos hacer notar las siguientes diferencias entre las dos demostraciones, la primera en donde usamos el cuantificador existe y en la que usamos todos.

Existen Blorgs que comen los viernes.	(todos) Los Blorgs comen un día antes de los Martes.
Se puede reescribir como $$\exists x P(x) $$	Se puede reescribir como $$\forall x P(x) $$
Consideramos un blorg «mañoso». Es decir, dentro del «conjunto» de los Blorgs, consideramos a uno estratégicamente que nos ayudara a demostrar que al menos un blorg cumplía la condición, en este caso un blurg.	Consideramos un blorg arbitrario (tuvimos que considerar distintos casos en los que el blorg fuera blarg, blerg o blurg)
Exhibimos el ejemplo de un blorg, que comía los viernes. Y con eso demostramso que la proposición se cumplía.	Llegamos a la conclusión de que sin importar cómo fuera el blorg, comía un dia antes de los Martes.

Esto nos quiere decir que cuando estemos hablando del cuantificador $\exists$, no necesitamos generalizar el caso, solo necesitamos exhibir un ejemplo donde la proposición se cumpla. Mientras que cuando hablamos de $\forall$, tenemos que generalizar, es decir, tenemos que considerar todos los casos posibles para probar que una afirmación sea verdadera o no.

Tratando con la unicidad.

Vamos a ver ahora un pequeño mapa de cómo viven los Blorgs en el mundo Blorg:

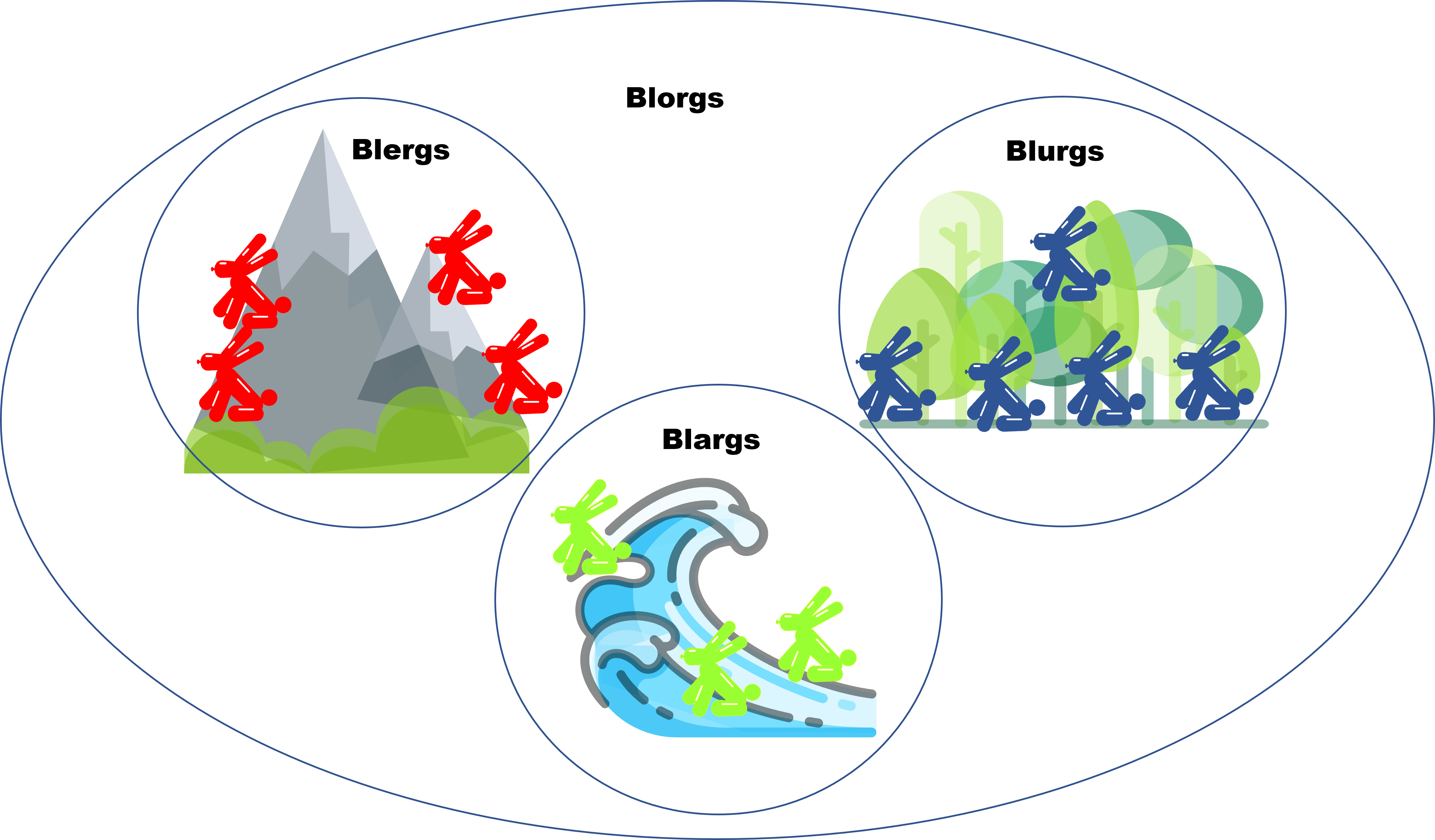
Este mapa muestra cómo se dividen los Blorgs, así que cuando estuvimos haciendo la demostración de existencia de los Blorgs que comen los Viernes, elegimos alguno de estos:

Mientras que cuando hablamos de $\forall$, tuvimos que comprobar que se cumplía para cualquiera de los Blorgs, ya fueran Blergs, Blargs o Blurgs. Pero aún falta otro cuantificador, que es el $\exists !$.

Ahora lee la siguiente proposición:

Proposición. Existe una única raza de Blorgs que dentro de su dieta puede haber fresas.

Nota que ahora no estamos hablando de los Blorgs como criaturas, sino de sus especies, y solo existen tres especies de blorg: Blargs, Blergs y Blurgs. Es decir, nos piden demostrar que entre estas tres, solo existe una que come fresas.

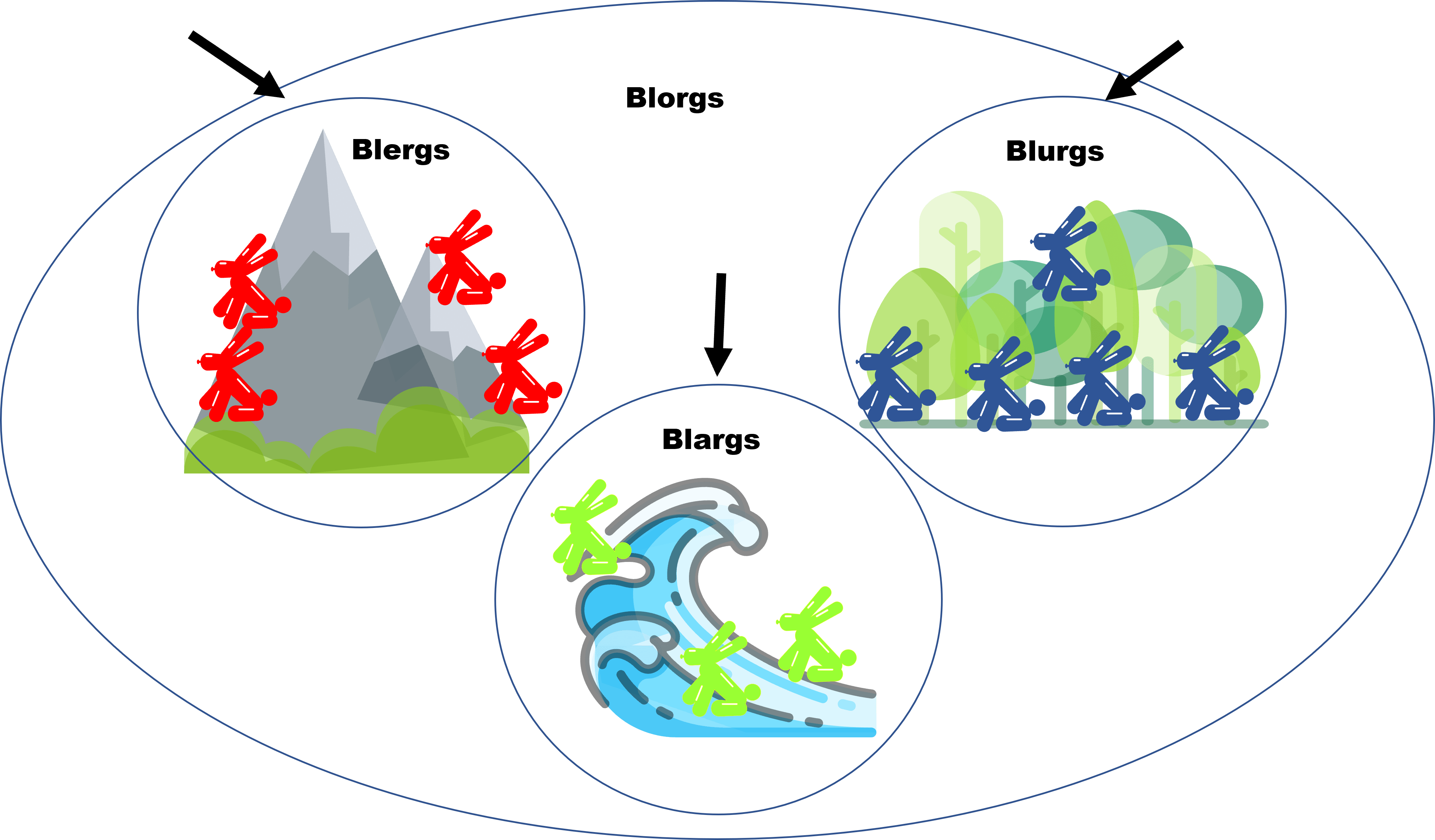
Entonces para demostrar que se cumple la proposición, tendremos que primero exhibir una especie que coma fresas y después demostrar que es única.

Demostración. Solo existen tres especies de Blorgs, notemos que dentro de estas, se encuentran los Blergs que comen frutos, por lo que son los Blergs quienes pueden incluir fresas en sus dietas.

(Hasta aquí hemos probado que existe una especie que puede comer fresas)

Ahora, para demostrar que es única, veamos que las otras dos razas solo comen peces, los cuales evidentemente no pueden incluir las fresas, por tanto esta especie es única.

(Así demostramos la unicidad)

$\square$

Esta es una proposición que se puede escribir como

$$\exists ! x P(x) $$

Entonces para demostrar el cuantificador $\exists ! x P(x)$, primero debemos demostrar $\exists x P(x)$ y después que es única. Nota que demostrar la unicidad, equivale a demostrar lo siguiente:

$$\exists! x P(x) = \exists x (P(x) \land \forall y \neq x (\neg P(y))) $$

Es decir «Existe $x$ que cumple $P(x)$ y todo elemento $y$ distinto a $x$, no cumple $P(y)$»

En nuestra demostración la primera parte antes del primer paréntesis, demostramos que existe $x$ (Blergs) que cumple $P(x)$. Mientras que en la segunda parte mostramos que todo elemento $y$ distinto a $x$(Blargs y Blurgs) , no cumple $P(y)$. Para la segunda parte, vimos que si $y$ no eran los Blergs, entonces no podían comer fresas.

Nos saltamos un conector, que es el $\nexists$, para demostrar estos casos, es suficiente notar que

$$\nexists x P(x) = \forall x (\neg P(x)) $$

Por ejemplo, para demostrar que «No existen especies de Blorgs que coman los miércoles», solo basta demostrar que todas las especies de Blorgs no comen los miércoles.

Algunos ejemplos de demostraciones con los cuantificadores que utilizan

A continuación mostramos algunos ejemplos de proposiciones y de qué cuantificador hablan ayudados de su escritura como lógica proposicional. No es necesario que entiendas a qué se refiere cada uno, pero nota cómo traducimos el enunciado a lógica proposicional.

Proposición	Proposición en lógica proposicional
Para todo $a$ número real, $a \leq |a|$ y $-a \leq |a|$	Sea $P(a)$ = $a \leq |a|$ y $-a \leq |a|$: $$\forall a \text{ número real } P(a)$$
El neutro aditivo es único en los números reales.	Sea $P(x)$ = $x$ es neutro aditivo: $$\exists ! x \text{ número real } P(x)$$
Para todo binomio con coeficientes reales (es de la forma $ax^2+b^x+c$ donde $a,b,c$ son números reales), existe solución compleja. *	Sea $P(p,x)$ = $p$ tiene solución compleja $x$: $$\forall p \text{ binomio con coeficientes reales } \exists x (P(p,x)) $$

Notas

*: Esta es una consecuencia de algo que se conoce como el «Teorema fundamental del álgebra», que se usa en un segundo curso de álgebra superior (la continuación de este curso). Sólo se utiliza, más no se demuestra. La herramienta necesaria para su demostración, normalmente se puede ver en un curso de Variable Compleja I, el cual corresponde hasta el tercer año de una licenciatura en matemáticas.

Más adelante…

Antes de terminar de estudiar estas «formas» de demostrar, vamos a terminar viendo el último conector que intencionalmente nos saltamos, este es la «doble implicación», y hay un motivo para ello, pues comúnmente te vas a encontrar este tipo de demostraciones y verás la técnica que se empleará.

Tarea moral

A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.

1. Demuestra que existen Blorgs que no viven dentro del agua.
2. Demuestra que todos los Blorgs comen al menos una vez a la semana.
3. Demuestra que existe una única especie de Blorgs que habla con animales con aletas.
4. Demuestra que no existe una especie de Blorgs que coman los miércoles.

Entradas relacionadas

• Ir a Álgebra Superior I
• Entrada anterior del curso: Demostración de proposiciones con conectores
• Siguiente entrada del curso: Problemas de demostraciones con conectores y cuantificadores

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE109323 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 3»