(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)
Introducción
En esta entrada repasaremos lo que vimos en la entrada anterior. Primero, veremos unos ejemplos que ilustran las definiciones de órbita y estabilizadores. A partir de estos ejemplos podremos observar ciertos patrones que se repiten y los analizaremos formalmente en una proposición. Por último, daremos un último ejemplo para ilustrar dicha proposición.
Ejemplos de Acciones
Repasemos lo que hemos visto con los siguientes ejemplos. En cada ejemplo describimos el grupo $G$, la órbita y los estabilizadores de los elementos.
Ejemplo 1. Consideremos la permutación $\alpha = (1\,2\,3\,4) \in S_6$. Sean $G = \left<\alpha\right>$ y $X = \{1,2,3,4,5,6\}$ con la acción dada por $\alpha^k \cdot i = \alpha^k(i)$ para toda $k\in \z, i\in X.$
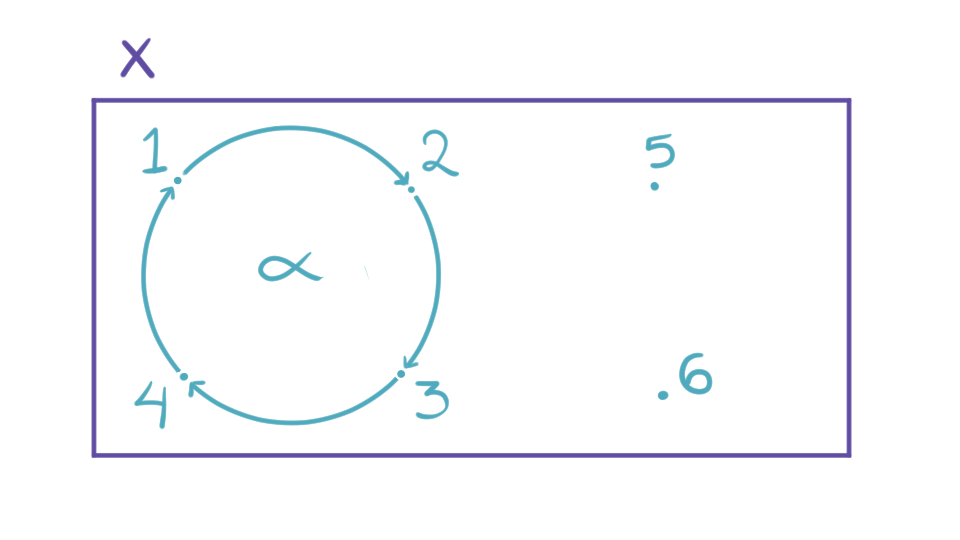
Además, $\alpha$ deja fijos al 5 y al 6.
Comencemos describiendo a las órbitas de los elementos:
\begin{align*}
\mathcal{O}(1) &= \{1,2,3,4\}\\
&= \mathcal{O}(2) = \mathcal{O}(3) = \mathcal{O}(4)\\
\mathcal{O}(5) &= \{5\}\\
\mathcal{O}(6) &= \{6\}.
\end{align*}
Observemos que las órbitas de $1, 2, 3$ y $4$ son iguales porque $\alpha$ es una permutación cíclica que mueve esos elementos, pero como $\alpha$ deja fijos a $5$ y a $6,$ sus órbitas son distintas y consisten solamente de sí mismos.
Ahora, podemos describir mejor a $G = \left< \alpha \right>$. Como $\alpha$ tiene orden 4, $G$ quedaría:
$$G = \{(1), \alpha, \alpha^2,\alpha^3\}.$$
Por último, describamos los estabilizadores. De acuerdo a la definición de la entrada previa el estabilizador de un objeto son los elementos del grupo que fijan al objeto, en este caso las potencias de $\alpha$ que dejan fijo al objeto. En el caso del $1$ la única potencia de $\alpha$ que lo fija es la identidad y análogamente para $2,3$ y $4$. Por otro lado en el caso de $5$ y $6$, como $\alpha$ no los mueve en absoluto, cualquier potencia de $\alpha$ forma parte de sus respectivos estabilizadores. Esto quedaría escrito de la siguiente manera:
\begin{align*}
G_1 &= \{\alpha^k \in G | \alpha^k \cdot 1 = 1\} = \{(1)\}\\
&= G_2 = G_3 = G_4. \\\\
G_5 &= \{\alpha^k \in G | \alpha^k \cdot 5 = 5\} = G = \{(1), \alpha, \alpha^2,\alpha^3\} \\&= \{\alpha^k \in G | \alpha^k \cdot 6 = 6\}\\
&= G_6.
\end{align*}
Ejemplo 2. Consideremos ahora la permutación $\beta = (1\,2\,3)(4\,5)\in S_5$. Sean $G = \left< \beta \right>$ y $X= \{1,2,3,4,5\}$ con la acción dada por $\beta^k \cdot i = \beta^k(i)$ para todas $k\in\z$ y $i\in X.$
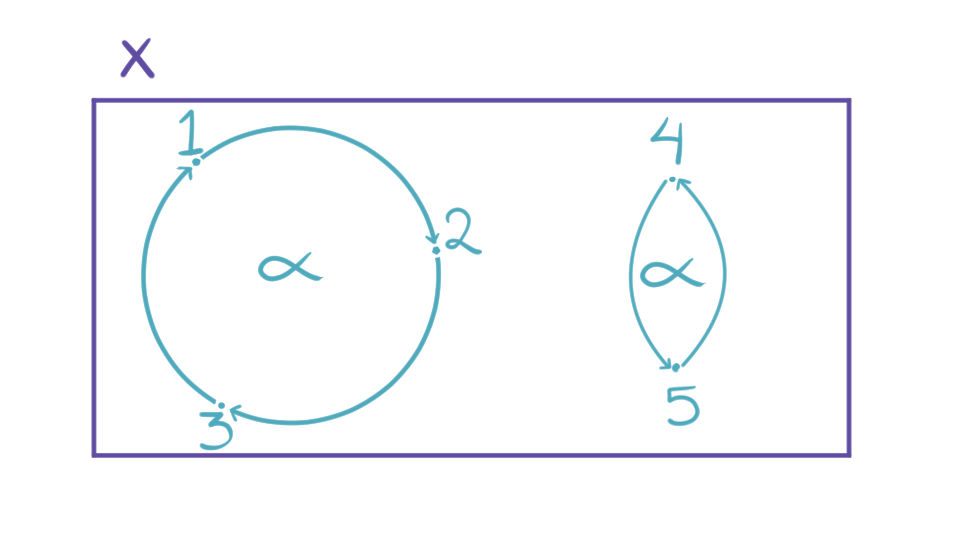
Primero, describamos las órbitas de los elementos:
\begin{align*}
\mathcal{O}(1) &= \{1,2,3\} = \mathcal{O}(2) = \mathcal{O}(3).\\
\mathcal{O}(4) &= \{4,5\} = \mathcal{O}(5).
\end{align*}
Ahora, describamos mejor a $G$. Observemos que $\beta$ está compuesta por dos ciclos disjuntos: $(1\, 2\, 3)$ con orden $3$ y $(4\,5)$ con orden $2$, es decir es el producto de dos ciclos que conmutan y que tienen órdenes primos relativos entre sí. Por el último teorema de la entrada Palabras, el orden de $\beta$ es entonces $6$. Así, $G$ quedaría descrito como:
$$G = \{(1), \beta, \beta^2, \beta^3, \beta^4,\beta^5\}.$$
Por último, describamos los estabilizadores de cada elemento.
\begin{align*}
G_1 &= \{\beta^k \in G | \beta^k(1) = 1\} = \{(1),\beta^3\}\\
&= G_2 = G_3. \\\\
G_4 &= \{\beta^k\in G | \beta^k(4) = 4\} = \{(1), \beta^2, \beta^4\}\\
&= \{\beta^k\in G | \beta^k(5) = 5\} \\
&= G_5.
\end{align*}
Antes de avanzar a la siguiente sección, considera los ejemplos estudiados e intenta determinar si existe alguna relación entre $\#\mathcal{O}(x)$, $|G_x|$ y $|G|$.
¿Qué relación existe entre el tamaño de la órbita y el tamaño del estabilizador de un elemento?
Los ejemplos que trabajamos al inicio de esta entrada nos pueden dar la idea de que existe algún tipo de relación entre los tamaños de la órbita y del estabilizador para cada elemento.
Proposición. Sean $G$ un grupo, $X$ un $G$-conjunto y $x\in X$.
\begin{align*}
\#\mathcal{O}(x) = [ G:G_x].
\end{align*}
Demostración.
Sea $G$ un grupo, $X$ un $G$-conjunto y $x\in X$. Dado que $[ G:G_x]=\# \{gG_x| g\in G\}$ bastaría con encontrar una biyección entre $\mathcal{O}(x)$ y $\{gG_x| g\in G\}.$
Proponemos $\varphi : \mathcal{O}(x) \to \{gG_x| g\in G\}$ tal que $g\cdot x \to g G_x$ para todo $g\in G.$
Debemos probar que $\varphi$ es una biyección.
Primero, veamos que está bien definida. Tomemos $g,h\in G$, y supongamos que $g\cdot x = h\cdot x$.
Multiplicamos ambos lados por $h^{-1}$. Esto queda,
\begin{align}\label{ec1}
h^{-1}\cdot (g\cdot x) &= h^{-1}\cdot (h\cdot x).
\end{align}
Por las propiedades de acción, al desarrollar la parte derecha de la igualdad \ref{ec1} obtenemos
\begin{align*}
h^{-1}\cdot (h\cdot x) &= (h^{-1}h)\cdot x\\
&= e\cdot x = x.
\end{align*}
Por otro lado al desarrollar la parte izquierda de la igualdad \ref{ec1} obtenemos que,
\begin{align*}
h^{-1}\cdot(g\cdot x) = (h^{-1}g)\cdot x.
\end{align*}
Así, $ (h^{-1}g)\cdot x=x$ y esto por definición quiere decir que $h^{-1}g\in G_x$.
Por lo que estudiamos en clases laterales, esto implica que $gG_x = hG_x$, es decir que $\varphi(g\cdot x)=\varphi(h\cdot x)$.
Así, concluimos que $\varphi$ está bien definida.
Ahora, probaremos que $\varphi$ es inyectiva.
Sean $g, h \in G$, tales que $\varphi(g\cdot x) = \varphi(h\cdot x)$, es decir tales que $g G_x = hG_x.$ Pero
\begin{align*}
g G_x &= hG_x\\
\Rightarrow &h^{-1} g\in G_x &\text{Por lo que sabemos de clases laterales}\\
\Rightarrow &(h^{-1}g)\cdot x = x & \text{Por estar en el estabilizador}\\
\Rightarrow &h\cdot ((h^{-1}g)\cdot x) = h\cdot x. &\text{Haciendo actuar $h$}\\ \Rightarrow &g\cdot x=((hh^{-1})g)\cdot x =(h(h^{-1}g))\cdot x =h\cdot ((h^{-1}g)\cdot x) = h\cdot x. &\text{Por las propiedades de acción.}\\
\end{align*}
Así $\varphi$ es inyectiva.
Por construcción podemos observar que $\varphi$ es suprayectiva.
Por lo tanto $\#\mathcal{O} = [ G:G_x]$.
$\blacksquare$
Como consecuencia de lo anterior obtenemos el siguiente corolario.
Corolario. Sean $G$ un grupo finito, $X$ un $G$-conjunto y $x\in X.$ Entonces, $\# \mathcal{O}(x)$ divide a $|G|.$
Ejemplo del Dodecaedro
Veamos un ejemplo en el que apliquemos lo que acabamos de ver.
Consideremos el dodecaedro $D$.
Si pensamos en todas las simetrías en $\r^3$ que mandan el dodecaedro en sí mismo, podemos tomar las rotaciones y así definir $G = \{\varphi \text{ rotación en }\r^3 | \varphi[D]= D\}$.
¿Cuál es el orden de $G$?
Sea $X$ el conjunto de caras de $D$. Entonces, $G$ actúa en $X$ ya que manda caras de $D$ en caras de $D$. La acción es transitiva ya que cada cara se puede llevar a cualquier cara contigua mediante una rotación de $\displaystyle\frac{2\pi}{3}.$
Si el eje de rotación va del origen a un vértice, las caras rotarán tomando el lugar de otras caras. En cambio, si el eje de rotación cruza del origen al centro de una cara, esa cara rotará sobre sí misma y cada que rote $\displaystyle r = \frac{2\pi}{5}$ seguirá en su lugar.
Así, dado $x\in X$, habrá exactamente cinco rotaciones que mandan la cara $x$ en sí misma (aquellas rotaciones de ángulo $ \frac{2\pi}{5}$ cuyo eje de rotación cruza del origen al centro de una cara), por lo cual $|G_x| = 5$. Además, como la acción es transitiva $\# X = \#\mathcal{O}(x)$. Luego, $\#X = 12$ y $\#\mathcal{O}(x) = [G:G_x ]$. Pero $\displaystyle [G:G_x ] = \frac{|G|}{5}$. Si juntamos todo eso, obtenemos:
$$12 = \# X = \#\mathcal{O}(x) = [G:G_x ]= \frac{|G|}{5}.$$
Despejando, $|G| = 12\cdot 5 = 60.$ Es decir, tenemos 60 rotaciones en $\r^3$ que son simetrías del dodecaedro.
Tarea moral
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Sea $G$ un grupo finito actuando sobre sí mismo:
- Determina si el hecho de que exista $x\in G$ y tal que $G_x =\{e\}$ implica que la acción es transitiva.
- Determina si el hecho de que la acción sea transitiva implica que exista $x\in G$ tal que $G_x =\{e\}$.
- Encuentra el orden del grupo de simetrías de cada sólido platónico (recuerda que hay algunos que son duales y por lo tanto tienen el mismo grupo de simetrías).
Más adelante…
Ya casi acabamos de estudiar la órbita, todavía nos queda analizar con más detalle el caso cuando $X=G$, es decir cuando $G$ actúa sobre sí mismo. También podemos preguntarnos qué sucede con el conjunto de elementos de $X$ que se quedan fijos ante cualquier elemento de $G$ que actúe sobre ellos. Esto nos servirá para llegar a una importante ecuación llamada la ecuación de clase.
Además, en la siguiente entrada definiremos un nuevo tipo de grupo conocido como $p$-grupo y esto nos perfilará para llegar a los Teoremas de Sylow.
Entradas relacionadas
- Ir a Álgebra Moderna I.
- Entrada anterior del curso: Órbita de $x$ y tipos de acciones.
- Siguiente entrada del curso: Clases de Conjugación, Centro de $G$, Ecuación de Clase y $p$-Grupo.
- Resto de cursos: Cursos.