(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Tomemos un grupo $G$ y $X$ un $G$-conjunto. A lo largo de esta entrada consideraremos la relación de equivalencia en $X$ inducida por esta acción y que fue definida en la entrada anterior de la siguiente manera:

$x\sim y$ si y sólo si $g\cdot x=y$ para algún $g\in G$.

Continuemos entonces con esta idea, comenzando por definir las clases de equivalencia inducidas por esa relación.

Después, definiremos nuevos tipos de acciones, por ejemplo, ¿qué pasa si la relación sólo induce una clase de equivalencia? o ¿qué sucede con el conjunto de objetos que dejan fijo a los elementos de $G$?

Órbita de un elemento de $X$

Dada la importancia de esta manera de relacionar a los elementos de un grupo de acuerdo a una acción, daremos un nombre a sus clases de equivalencia.

Definición. Sean $G$ un grupo, $X$ un $G$-conjunto. Para cada $x\in X$, la órbita de $x$ es
$$\begin{array}{r}\mathcal{O}(x)=\{g\cdot x|g\in G\},\end{array}$$

es decir, todos los objetos que podemos obtener haciendo actuar a $G$ sobre $x$.

Observación. Sean $G$ un grupo, $X$ un $G$-conjunto. Tenemos que $\mathcal{O}(x)$ es la clase de equivalencia de $x$ con respecto a la relación inducida por la acción de $G$ en $X$.

Demostración.

Sea $x\in G$. Sabemos que la clase de equivalencia de $x$, denotada por $[x]$, se define como:
$$\begin{array}{rlr}[x]& =\{y\in X|x\sim y\}& \text{Definición de clase de equivalencia}\\ & =\{y\in X|\mathrm{\exists }g\in G\text{ con }g\cdot x=y\}& \text{Definición de la relación }\sim \\ & =\{g\cdot x|g\in G\}=\mathcal{O}(x)& \text{Definición de órbita.}\end{array}$$

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

De cursos anteriores sabemos que la colección de clases de equivalencia inducidas por una relación es una partición del conjunto. El siguiente teorema se da como consecuencia de las propiedades de una partición.

Teorema. Sean $G$ un grupo, $X$ un $G$-conjunto. Entonces

1. $\mathcal{O}(x)\ne \mathrm{\varnothing }$ para toda $x\in X$.
2. Sean $x,y\in X$. Si $\mathcal{O}(x)\cap \mathcal{O}(y)\ne \mathrm{\varnothing }$, entonces $\mathcal{O}(x)=\mathcal{O}(y)$.
3. ${\displaystyle X=\bigcup _{x\in X}\mathcal{O}(x)}$.

Este teorema sólo enlista las propiedades de una partición en el caso particular en el que estamos trabajando, por lo que no hay nada nuevo que demostrar.

Una acción transitiva

Las órbitas están determinadas por varios factores: el conjunto $X$, el grupo $G$ y la acción de $G$ en $X$. En algunos casos existe una única órbita.

Definición. Sean $G$ un grupo, $X$ un $G$-conjunto. Si $\mathcal{O}(x)=X$ para alguna $x\in X$, decimos que la acción es transitiva.

Esta definición nos dice que podemos obtener cualesquier elemento de $X$ haciendo actuar algún elemento del grupo en el objeto $x$.

Ejemplos de acciones transitivas

Ejemplo 1. Dado $G$ un grupo, $X=G$ definimos la acción de $G$ en sí mismo mediante la operación de $G$, es decir $a\cdot x=ax$ para todas $a\in G$, $x\in X.$

Consideremos cualquier $x\in X$. Sea $y\in X$. Siempre tenemos una manera de obtener $y$ a través de $x$:
$$\begin{array}{rl}y=y(x^{-1}x)=(y{x}^{-1})x=(y{x}^{-1})\cdot & x\in \mathcal{O}(x).\\ \text{Entonces }& y\in \mathcal{O}(x).\end{array}$$

Por lo tanto $\mathcal{O}(x)=X$ y así la acción es transitiva.

Ejemplo 2. Sean $G$ un grupo, $H\le G$, $X=\{gH|g\in G\}$. Definimos $a\cdot (gH)=agH$ para todas $a,g\in G.$

Consideremos cualquier $gH\in X.$ Sea $tH\in X$ con $t\in G.$ Podemos reescribir al representante como:
$$\begin{array}{rl}tH& =t(g^{-1}g)H=(t{g}^{-1})gH\\ & =(t{g}^{-1})\cdot gH\in \mathcal{O}(gH).\end{array}$$

Por lo tanto $\mathcal{O}(gH)=X$. Así, la acción es transitiva.

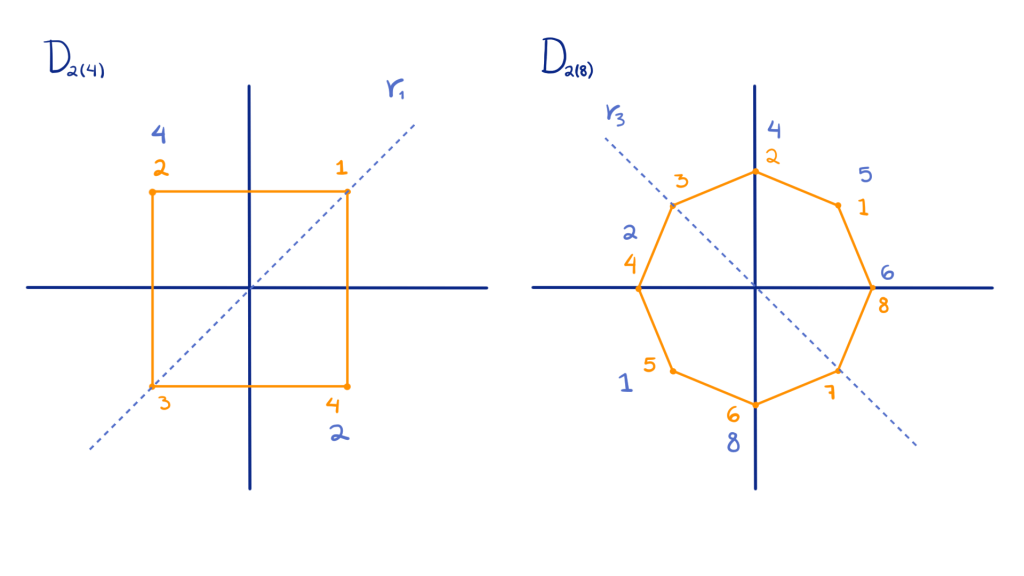
Ejemplo 3. Sea $G=D_{2(n)}$ el grupo diédrico, $X=\{1,2,\cdots ,n\}$ los distintos vértices del polígono regular de $n$ lados.

La acción que ya habíamos trabajado: dados $g\in G$, $i\in X$ definimos $g\cdot i=g(i)$.

Dada $a\in G$ la rotación ${\displaystyle \frac{2\pi }{n}}$ y $1\in X$, tenemos que
$$\begin{array}{rl}\text{id}\cdot 1& =1,\\ a\cdot 1=a(1)& =2,\\ a^2\cdot 1=a^2(1)& =3,\\ & ⋮\\ a^{n-1}\cdot 1=a^{n-1}(1)& =n.\end{array}$$

Entonces $X=\{1,2,\cdots ,n\}\subseteq \mathcal{O}(1)\subseteq X$. Así, $\mathcal{O}(1)=X$. Por lo tanto la acción es transitiva.

Ejemplo 4. Ahora veamos un ejemplo nuevo.

Sea $G$ un grupo, $X=G$. Dados $a\in G$, $x\in X$ definimos
$$\begin{array}{rl}a\cdot x& =ax{a}^{-1}.\end{array}$$

Demostremos que es una acción:
$$\begin{array}{rlr}e\cdot x& =ex{e}^{-1}=x& \mathrm{\forall }x\in X.\\ a\cdot (b\cdot x)& =a(b\cdot x)a^{-1}=a(bx{b}^{-1})a^{-1}=(ab)x(ab{)}^{-1}& \text{Asociando diferente}\\ & =(ab)\cdot x& \mathrm{\forall }a,b\in G,\mathrm{\forall }x\in X.\end{array}$$

Así, $G$ actúa en sí mismo por conjugación.

Dado $x\in X$,
$$\begin{array}{r}\mathcal{O}(x)=\{g\cdot x|g\in G\}=\{gx{g}^{-1}|g\in G\}\end{array}$$
que son todos los conjugados de $x$.

En este caso, la acción no siempre es transitiva: Si $G\ne \{e\}$ consideremos $x\in G\setminus \{e\}.$ Si $e\in \mathcal{O}(x)$ entonces $e=g\cdot x=gx{g}^{-1}$ para algún $g\in G$ y entonces $e=x$, esto es una contradicción porque $x\in G\setminus \{e\}$. Así, $\mathcal{O}(x)\ne X$ y la acción no es transitiva.

Más definiciones de acciones

En toda acción el neutro del grupo actúa de forma trivial en todos los elementos del conjunto pero puede ser que existan otros elementos del grupo con esa propiedad. Si no es el caso decimos que la acción es fiel:

Definición. Sea $G$ un grupo, $X$ un $G$-conjunto. Decimos que la acción es fiel si $g\cdot x=x$, con $g\in G$, para todo $x\in X$, implica que $g=e.$

Consideremos ahora los elementos del grupo que fijan a algún elemento específico del conjunto:

Definición. Sea $G$ un grupo, $X$ un $G$-conjunto, $x\in X$. El estabilizador de $x$ es
$$\begin{array}{r}{G}_x=\{g\in G|g\cdot x=x\}.\end{array}$$

Es decir, la colección de todos los elementos de $G$ que dejan fijo a $x$.

Ejemplos de acción fiel y estabilizador

Ejemplo 1. Sea $G$ un grupo, $X=G$ y $g\cdot x=gx$ para todo $g,x\in G.$

Si $g\in G$ es tal que $g\cdot x=x$ para toda $x\in X$, entonces $gx=x$ para toda $x\in X$, en particular $g=ge=e.$

Así $g=e$ y la acción es fiel.

Dado $x\in X$,
$$\begin{array}{r}{G}_x=\{g\in G|g\cdot x=x\}=\{g\in X|gx=x\}.\end{array}$$

Pero si $gx=x$,por cancelación $g=e$. Así $G_x=\{e\}$ para toda $x\in X,$ de modo que los estabilizadores son triviales.

Ejemplo 2. Sean $G$ grupo, $H$ subgrupo de $G$, $X=\{xH|x\in G\}$ con $g\cdot (xH)=gxH$ para toda $g,x\in G.$

Si $g\in G$ es tal que $g\cdot (xH)=xH$ para toda $x\in G$, entonces
$$\begin{array}{rlr}gxH& =xH& \mathrm{\forall }x\in G\\ \Rightarrow x^{-1}gx& \in H& \mathrm{\forall }x\in G\\ \Rightarrow g& \in xH{x}^{-1}& \mathrm{\forall }x\in G.\end{array}$$

Si $H⊴G$ esto se cumple para toda $g\in H$. Por lo tanto la acción no necesariamente es fiel.

Ahora, dada una clase lateral $xH\in X$.
$$\begin{array}{rl}{G}_{xH}& =\{g\in G|g\cdot (xH)=xH\}\\ & =\{g\in G|gxH=xH\}\\ & =\{g\in G|x^{-1}gx\in H\}\\ & =\{g\in G|g\in xH{x}^{-1}\}\\ & =xH{x}^{-1}.\end{array}$$

Así $G_{xH}=xH{x}^{-1}$ para toda $x\in G.$

Ejemplo 3. Sean $G=D_{2(n)}$ el grupo diédrico, $X=\{1,2,\cdots ,n\}$ los distintos vértices del polígono regular de $n$ lados.

Dados $g\in G,i\in X$ definimos $g\cdot i=g(i)$.

Si $g\in G$ es tal que $g\cdot i=i$ para toda $i\in X$, entonces $g(i)=i$ para toda $i\in X$. Así, $g$ sería una transformación lineal en el plano, que fija a los vértices $1$ y $2,$ los cuales forman una base del plano. Por lo tanto $g=\text{id}$ y la acción es fiel.

Dado $i\in X$,
$$\begin{array}{rl}{G}_i& =\{g\in G|g\cdot i=i\}\\ & =\{g\in G|g(i)=i\}\\ & =\{\text{id},r_i\}\end{array}$$
con $r_i$ la reflexión con respecto a la recta que pasa por $(0,0)$ y $i.$

Por último, veremos una observación.

Observación. Sea $G$ un grupo, $X$ un $G$-conjunto, $x\in X$. $G_x$ es un subgrupo de $G$.

Demostración.
Sean $G$ grupo, $X$ un $G$-conjunto, $x\in X.$

El neutro de $G$ siempre está en el estabilizador porque:
$$\begin{array}{r}e\cdot x=x\mathrm{\forall }x\in X,\end{array}$$

entonces $e\in G_x.$

Si $a,b\in G_x$, entonces $(ab)\cdot x=a\cdot (b\cdot x)=a\cdot x=x=x$. Así, $ab\in G_x$. Es decir, el estabilizador es cerrado bajo producto.

Finalmente si $a\in G_x$, $a\cdot x=x$, entonces $a^{-1}\cdot x=a^{-1}\cdot (a\cdot x)=(a^{-1}a)\cdot x=e\cdot x=x$, así $a^{-1}\in G_x$.

Por lo tanto $G_x\le G$.

$\mathrm{<img\; draggable="false"\; role="img"\; class="emoji"\; alt="◼"\; src="https://s.w.org/images/core/emoji/14.0.0/svg/25fc.svg">}$

Tarea moral

1. En cada uno de los incisos del ejercicio 1 de la entrada de acciones, en donde haya una acción, describe cómo son las órbitas y determina si se trata de una acción transitiva.
2. Considera el conjunto $X=\{1,2,3,4,5,6,7,8\}$ y el grupo $G=⟨a⟩$ con $a\in S_8$. Define $a^i\cdot j=a^i(j)$ para cada $a^i\in G$ y cada $j\in X$.
   • Verifica que es una acción de $G$ en $X$.
   • Si $a=(24178)$ describe las órbitas y determina si se trata de una acción transitiva.
   • Si $a=(6158)(34)$ describe órbitas y determina si se trata de una acción transitiva.
3. Sea $G$ un grupo y $X$ un $G$-conjunto. Si la acción de transitiva prueba o da un contraejemplo para las siguientes afirmaciones:
   • $\mathcal{O}(x)=X$ para todo $x\in X$.
   • Para cada $x,y\in X$ existe $g\in G$ tal que $g\cdot x=y$.
4. Considera el grupo diédrico $D_{2(n)}$ actuando sobre sí mismo con conjugación.
   • Determina si la acción es fiel.
   • Encuentra el estabilizador de $a$, con $a$ la rotación de ${\displaystyle \frac{2\pi }{n}}$, y el de $b$ con $b$ la reflexión con respecto al eje $x$.
5. Sea $G$ un grupo y $X$ un $G$-conjunto.
   • Determina si el hecho de que exista $x\in G$ tal que $G_x=\{e\}$ implica que la acción es fiel.
   • Determina si el hecho de que la acción sea fiel implica que exista $x\in G$ tal que $G_x=\{e\}$.

Más adelante…

Continuaremos estudiando las propiedades de las órbitas, en particular, el orden de las órbitas, ¿cómo se relaciona éste con el orden del grupo $G$? Daremos respuesta a ello en la siguiente entrada.

Entradas relacionadas

• Ir a Álgebra Moderna I.
• Entrada anterior del curso: Acciones.
• Siguiente entrada del curso: Tamaño de una órbita y de un estabilizador.
• Resto de cursos: Cursos.