(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)

Introducción

Dado un conjunto podemos considerar colecciones formadas por algunos de sus elementos. Estudiaremos estas colecciones que como veremos son también conjuntos y por ende objetos de estudio de la teoría de conjuntos. En esta nota estudiaremos el concepto de subconjunto y a partir de ello estableceremos cuándo dos conjuntos se considerarán iguales. Se desarrollarán pruebas matemáticas intentando explicar a detalle cómo se realizan. Es conveniente que prestes mucha atención a estas demostraciones ya que a lo largo de tus estudios requerirás realizar y entender muchas pruebas y éstas son una parte esencial en las matemáticas.

Definición.

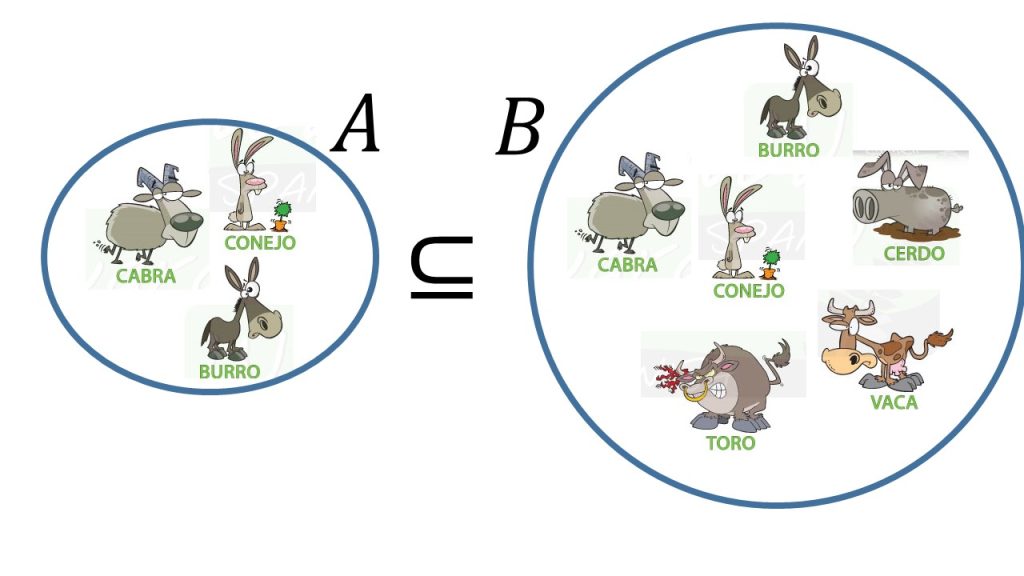
Dados $A$,$B$ conjuntos, decimos que $A$ es un subconjunto de $B$ si todo elemento de $A$ es un elemento de $B$, es decir si para toda $z$, $z\in A$ implica que $z\in B$.

En este caso decimos que $A$ está contenido en $B$ o que $B$ contiene al conjunto $A$.

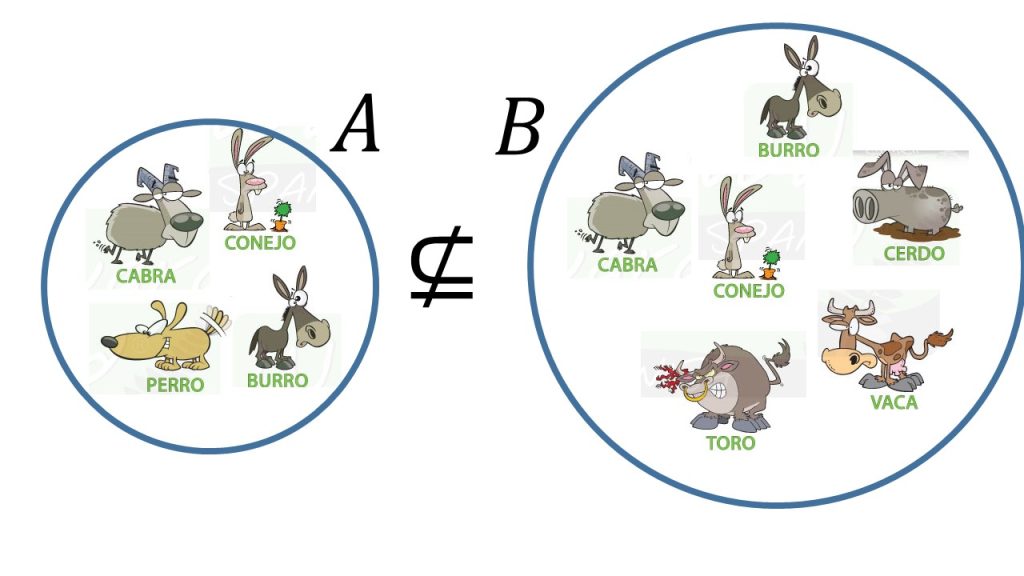
Nota que $A$ no está contenido en $B$, si existe al menos un $z$, tal que $z\in A$, pero $z\notin B$.

Notación:

Se escribe: $A\subseteq B$ si $A$ está contenido en $B$.

Se escribe: $A\nsubseteq B$ si $A$ no está contenido en $B$.

Si $A$ está contenido en $B$, pero $B$ no está contenido en $A$, decimos que la contención es propia o que $A$ es un subconjunto propio de $B$ y se denota por $A\subsetneq B$ (en este caso si $z\in A$, entonces $z\in B$, pero existe al menos un $z\in B$ tal que $z\notin A$).

Como se mencionó en la nota previa, los números naturales serán conjuntos y resultarán ser distintos como conjuntos cuando sean distintos como números, ver la sección 5.1, página 207, del libro de Avella y Campero que se menciona en la bibliografía de este curso. Para el siguiente ejemplo consideraremos, como usualmente lo hacemos, que los números $1,2,3$ y $4$ son distintos entre sí.

Ejemplo 1

$\set{1,2,3}\subseteq \set{1,2,3}$ ya que los elementos de $\set{1,2,3}$ son $1,2$ y $3$ y cada uno de ellos es un elemento de $\set{1,2,3}$.

$\set{1,2,3}\subseteq \set{1,2,3,4}$ ya que los elementos de $\set{1,2,3}$ son $1,2$ y $3$ y cada uno de ellos es un elemento de $\set{1,2,3,4}$.

$\set{1,2,3, 4}\nsubseteq \set{1,2,3}$ ya que $4\in \set{1,2,3, 4}$ pero $4\notin \set{1,2,3}$ pues $4$ es distinto de $1,2$ y $3$.

$\set{1,2,3}\subsetneq \set{1,2,3,4}$ ya que $\set{1,2,3}\subseteq \set{1,2,3,4}$ pero $\set{1,2,3, 4}\nsubseteq \set{1,2,3}$.

Así, es correcto decir que $\set{1,2,3}$ es un subconjunto de $\set{1,2,3,4}$, pero también que $\set{1,2,3}$ es un subconjunto propio de $\set{1,2,3,4}$, simplemente en el segundo enunciado estamos siendo un poco más precisos.

Proposición

Sean $A$, $B$, $C$ conjuntos.

1. $A\subseteq A$, es decir, cada conjunto se contiene a sí mismo.
2. Si $A\subseteq B$ y $B\subseteq C$, se tiene que $A\subseteq C$. Este hecho se conoce como la propiedad transitiva de la contención de conjuntos.
3. $\emptyset\subseteq A$, es decir, el conjunto vacío es subconjunto de cualquier conjunto.
   

Fíjate muy bien cómo se hace una prueba. Vamos a partir de una afirmación que consideraremos válida, a la que llamaremos hipótesis, y probaremos su consecuencia mediante razonamientos lógicos usando las definiciones o resultados previos.

Demostración de 1
En este primer caso:
La hipótesis es que $A$ es un conjunto cualquiera.
la consecuencia o lo que queremos demostrar es que $A\subseteq A$.
Demostración:
Como queremos probar que un conjunto es subconjunto de otro, entonces tenemos que verificar que la definición de subconjunto se satisface, recuerda que

$A\subseteq B$ si y sólo si para toda $z$, $z\in A$ implica que $z\in B$,

pero en nuestro caso $B=A$. Así, sea $z\in A$, entonces tenemos que $z\in A$. Por lo tanto tenemos que $A\subseteq A$.

$\square$

Demostración de 2

La hipótesis ahora es que $A,B$ y $C$ son conjuntos, con $A\subseteq B$ y $B\subseteq C$
y lo que se tiene que demostrar es que $A\subseteq C$
Demostración:
Dado que queremos probar que $A\subseteq C$, debemos ver que cualquier elemento en $A$ es también un elemento de $C$. Así, consideremos $z\in A$ y verifiquemos que $z\in C$. Como $A\subseteq B$ y $z\in A$, entonces por la definición de subconjunto $z\in B$, y como $B\subseteq C$, nuevamente por la definición de subconjunto $z\in C$. Con ello hemos verificado que para toda $z$, $z\in A$ implica $z\in C$ lo cual es la definición de que $A\subseteq C$, que es exactamente lo que queríamos demostrar.

$\square$

Demostración de 3

De nuevo la hipótesis es que $A$ es un conjunto cualquiera.
lo que queremos demostrar es que el conjunto vacío es un subconjunto de $A$, i.e. $\emptyset\subseteq A$.
Demostración:
Esta prueba la haremos por un método llamado contradicción, el cual consiste en negar la conclusión a la que queremos llegar, manteniendo las mismas hipótesis, y llegar a una contradicción de los teoremas o axiomas de la teoría que se está construyendo.
Primero neguemos la conclusión:

Existe algún conjunto $A$, tal que $\emptyset\nsubseteq A$.

Después se procede a encontrar la contradicción:

Si esto sucediera, es decir si $\emptyset\nsubseteq A$, entonces existiría al menos un elemento en el conjunto $\emptyset$, que no sería elemento del conjunto $A$, pero eso es dar por hecho que el conjunto $\emptyset$ tiene elementos lo cual está en contradicción con el axioma de conjunto vacío visto en la nota anterior.

La contradicción viene de suponer que existe algún conjunto $A$, tal que $\emptyset\nsubseteq A$, por lo tanto no puede existir dicho subconjunto probando así que $\emptyset\subseteq A$ para todo conjunto $A$.

$\square$

Ahora procederemos a dar dos axiomas más, el primero establece cuándo dos conjuntos serán considerados iguales.

Axioma de extensionalidad

Dos conjuntos son iguales cuando tienen exactamente los mismos elementos. Es decir, si $A$ y $B$ son conjuntos:

• $A=B$ significa que $A\subseteq B$ y $B\subseteq A$.
• $A\neq B$ significa que $A\nsubseteq B$ o $B\nsubseteq A$.

Ejemplos

2. Veamos que $\emptyset\neq \{\emptyset\}$.

Notemos que $\emptyset\subseteq \{\emptyset\}$ (ya que por la proposición anterior $\emptyset\subseteq A$ para todo conjunto $A$). Por otro lado recordemos que el conjunto vacío no tiene elementos, así que $A\notin \emptyset$ para todo conjunto $A$, en particular $\emptyset\notin \emptyset$. Tenemos entonces que $\{\emptyset\}\nsubseteq \emptyset$ ya que el único elemento de $\{\emptyset\}$, que es $\emptyset$, no es un elemento del conjunto $\emptyset$.

Así, $\emptyset\subseteq \{\emptyset\}$ pero $\{\emptyset\}\nsubseteq \emptyset$, por lo tanto $\emptyset\neq \{\emptyset\}$. (Intuitivamente podemos imaginar a los conjuntos como cajas y de esa forma $\emptyset$ sería una caja vacía, mientras que $ \{\emptyset\}$ sería una caja que tiene dentro una caja vacía, por lo que tiene sentido considerarlos distintos, ya que la primera caja no tiene nada, mientras que la segunda sí, tiene dentro una caja vacía).

3. Veamos que que $\{\emptyset\}\neq\{\{\emptyset\}\}$.

$\{\emptyset\}\nsubseteq\{\{\emptyset\}\}$ ya que el único elemento de $\{\emptyset\}$, el conjunto $\emptyset$, no es un elemento de $\{\{\emptyset\}\}$, pues el único elemento de $\{\{\emptyset\}\}$ es $\{\emptyset\}$ y como se vio en el ejemplo previo $\emptyset\neq \{\emptyset\}$.

Así, podemos concluir que $\{\emptyset\}\neq\{\{\emptyset\}\}$.

4. Consideremos el conjunto $C$ cuyos elementos son el conjunto vacío, $\emptyset$ y el unitario del vacío, $\{\emptyset\}$, es decir $C=\{\emptyset,\{\emptyset\}\}$. Observamos que:

$\emptyset\in \{\emptyset,\{\emptyset\}\}$ y $\{\emptyset\}\in \{\emptyset,\{\emptyset\}\}$ ya que por construcción $\emptyset$ y $\{\emptyset\}$ son los elementos de $C$.

$\emptyset\subseteq \{\emptyset,\{\emptyset\}\}$ ya que por la proposición previa $\emptyset\subseteq A$ para todo conjunto $A$, en particular $\emptyset\subseteq C$.

$\{\emptyset\}\subseteq \{\emptyset,\{\emptyset\}\}$ ya que el único elemento de $\{\emptyset\}$, que es $\emptyset$, es también un elemento de $\{\emptyset,\{\emptyset\}\}$.

$\{\emptyset,\{\emptyset\}\}\nsubseteq \{\emptyset\}$ ya que existe un elemento en $\{\emptyset,\{\emptyset\}\}$, el elemento $\{\emptyset\}$, que no es un elemento de $\{\emptyset\}$ (ya que el único elemento en $\{\emptyset\}$ es $\emptyset$ y por el ejemplo anterior $\{\emptyset\}\neq \emptyset$).

$\{\{\emptyset\}\}\subseteq \{\emptyset,\{\emptyset\}\}$ ya que el único elemento de $\{\{\emptyset\}\}$, que es $\{\emptyset\}$, es también un elemento de $\{\emptyset,\{\emptyset\}\}$.

Notemos que $\{\{\emptyset\}\}\neq\emptyset$ ya que el único elemento de $\{\{\emptyset\}\}$, que es $\{\emptyset\}$, no es un elemento de $\emptyset$ pues el conjunto vacío no tiene elementos. Por otro lado sabemos por el ejemplo 3 que $\{\{\emptyset\}\}\neq\{\emptyset\}$. Así,

$\{\{\emptyset\}\}\notin \{\emptyset,\{\emptyset\}\}$.

En este último ejemplo notamos que$\{\{\emptyset\}\}\subseteq \{\emptyset,\{\emptyset\}\}$ pero $\{\{\emptyset\}\}\notin \{\emptyset,\{\emptyset\}\}$, haciéndonos ver que las relaciones de pertenencia y de contención no son iguales por lo que debemos ser muy cuidadosos al usar una u otra.

El siguiente nos permite elegir elementos de un conjunto dado que tienen cierta característica en común para formar nuevos conjuntos.

Axioma de separación o de comprensión

Dado $A$ un conjunto y $P$ una propiedad, $\set{\,x\in A\mid\,x\,cumple\,P\,}$ es un conjunto.

Notemos que a diferencia de la colección considerada en la paradoja de Russell dada en la nota anterior, en este caso se considera, no a cualquier objeto con la propiedad $P$, sino a los objetos de algún conjunto que cumplen con la propiedad $P$, es decir partimos de un conjunto y tomamos ahí algunos de sus elementos.

Tarea Moral

1. Considera los conjuntos $B=\{x\in\mathbb{N}\,|\,x \text{ es un número primo}\}$, $C=\{x\in\mathbb{N}\,|\,x \text{ es un número primo y } x>2\}$ y $D=\{x\in\mathbb{N}\,|x\, \text{ es un número impar}\}$.

Determina si las siguientes afirmaciones son verdaderas o falsas:

$i)\,\, B \subseteq D$	$iv)\,\, C \subsetneq B$.
$i)\,\, B \subsetneq D$	$v) \,\, C \subseteq D$.
$iii)\,\, C \subseteq B$.	$vi) \,\, C \subsetneq D$.

2. Considera el conjunto $E=\{\emptyset,\{\{\emptyset\}\}\}$, determina si los siguientes objetos son elementos o subconjuntos de $E$:

$i)\,\, \emptyset\in E$.	$vii)\,\, \{\{\emptyset\}\}\subseteq E$.
$ii)\,\, \emptyset\subseteq E$.	$vii)\,\, \{\{\{\emptyset\}\}\}\in E$.
$iii)\,\, \{\emptyset\}\in E$.	$viii)\,\, \{\{\{\emptyset\}\}\}\subseteq E$.
$iv)\,\, \{\emptyset\}\subseteq E$.	$ix)\,\, \{\{\{\{\emptyset\}\}\}\}\in E$.
$v)\,\, \{\{\emptyset\}\}\in E$.	$x)\,\, \{\{\{\{\emptyset\}\}\}\}\subseteq E$.

3. Intenta hacer las pruebas de las proposiciones tú solo.

Más adelante

En la siguiente nota hablaremos del complemento de un conjunto y deduciremos propiedades básicas pero muy importantes asociadas a este concepto.

Entradas Relacionadas

Página principal del curso.

Nota anterior del curso. Nota 1 Noción de conjunto.

Nota siguiente del curso: Nota 3 El complemento de un conjunto.

Nota. Las imágenes mostradas para ilustrar los conjuntos no fueron de diseño propio, y se da las gracias a: https://www.spanish.cl/ por sus divertidos dibujos. Se deja el link de donde se obtuvieron: https://www.spanish.cl/vocabulario/animales-de-la-granja.htm.