$\textcolor{Red}{\textbf{Aproximación de Taylor para funciones $f:\mathbb{R}^{3}\rightarrow\mathbb{R}$}}$

El caso de la aproximación con $n=2$ nos queda
$$f(x,y)=f(x_{0},y_{0})+\textcolor{Blue}{\frac{1}{1!}\left(\frac{\partial f}{\partial x}(x_{0},y_{0})\cdot (x-x_{0})+\frac{\partial f}{\partial y}(x_{0},y_{0})\cdot (y-y_{0})\right)}+$$

$$\textcolor{Red}{\frac{1}{2!}\left(\frac{\partial^{2} f}{\partial x^{2}}(x_{0},y_{0})(x-x_{0})^{2}+2\frac{\partial^{2} f}{\partial x\partial y}(x_{0},y_{0})(x-x_{0})(y-y_{0})+\frac{\partial^{2} f}{\partial y^{2}}(x_{0},y_{0})(y-y_{0})^{2}\right)}+R_{2}$$
Donde la expresión azul se puede escribir

$$\textcolor{Blue}{\frac{1}{1!}\left(\frac{\partial f}{\partial x}(x_{0},y_{0})\cdot (x-x_{0})+\frac{\partial f}{\partial y}(x_{0},y_{0})\cdot (y-y_{0})\right)=\nabla f(x_{0},y_{0},z_{0})\cdot (h_{1},h_{2},h_{3})}$$
y la expresión en rojo

$$\textcolor{Red}{\frac{1}{2!}\left(\frac{\partial^{2}f}{\partial
x^{2}}{p}(x-x{0})^{2}+2\frac{\partial^{2}f}{\partial y \partial
x}{p}(x-x{0})(y-y_{0})+\frac{\partial^{2}f}{\partial
y^{2}}{p}(y-y{0})^{2}\right)}$$ Define una forma cuadratica que
podemos escribir

$$\textcolor{Red}{\frac{1}{2!}(x-x_{0}\quad y-y_{0})\left(\begin{array}{cc}
\frac{\partial^{2}f}{\partial x^{2}}&\frac{\partial^{2}f}{\partial y \partial x}\\
\frac{\partial^{2}f}{\partial x \partial y }&\frac{\partial^{2}f}{\partial y^{2}} \end{array}\right)\left(\begin{array}{c}
x-x_{0} \\y-y_{0} \end{array}\right)}$$

Por lo que el desarrollo de Taylor se puede escribir
$$f(x,y)=f(x_{0},y_{0})+\nabla f(x_{0},y_{0},z_{0})\cdot (h_{1},h_{2},h_{3})+\frac{1}{2!}(x-x_{0}\quad y-y_{0})\left(\begin{array}{cc}
\frac{\partial^{2}f}{\partial x^{2}}&\frac{\partial^{2}f}{\partial y \partial x} \\
\frac{\partial^{2}f}{\partial x \partial y }&\frac{\partial^{2}f}{\partial y^{2}} \end{array}\right)\left(\begin{array}{c}
x-x_{0} \\y-y_{0} \end{array}\right)$$

A la matriz

$$\left(\begin{array}{cc}
\frac{\partial^{2}f}{\partial x^{2}}&\frac{\partial^{2}f}{\partial y \partial x} \\
\frac{\partial^{2}f}{\partial x \partial y }&\frac{\partial^{2}f}{\partial y^{2}} \end{array}\right)$$

se le conoce como matriz Hessiana y se denota $H(x_{0},y_{0})$ por lo que el desarrollo de Taylor se puede escribir
$$f(x,y)=f(x_{0},y_{0})+\nabla f(x_{0},y_{0},z_{0})\cdot (h_{1},h_{2},h_{3})+\frac{1}{2!}(x-x_{0}\quad y-y_{0})(H(x_{0},y_{0}))\left(\begin{array}{c}
x-x_{0} \\y-y_{0} \end{array}\right)$$

$\textcolor{Red}{\textbf{Aproximación de Taylor para funciones $f:\mathbb{R}^{3}\rightarrow\mathbb{R}$}}$

Sea $f:A\subset\mathbb{R}^{3}\rightarrow\mathbb{R}$ y sea $F(t)=f(x_{0}+h_{1}t,y_{0}+h_{2}t,z_{0}+h_{3}t)$ con $t\in[0,1]$, de esta manera f recorre el segmento de $[x_{0},y_{0},z_{0}]$ a $[x_{0}+h_{1}t,y_{0}+h_{2}t,z_{0}+h_{3}t]$. Se tiene entonces que usando la regla de la cadena

$$F'(t)=\frac{\partial f}{\partial x}(x_{0}+h_{1}t,y_{0}+h_{2}t,z_{0}+h_{3}t)\cdot \frac{d(x_{0}+h_{1}t)}{dt}+\frac{\partial f}{\partial y}(x_{0}+h_{1}t,y_{0}+h_{2}t,z_{0}+h_{3}t)\cdot \frac{d(y_{0}+h_{2}t)}{dt}+$$

$$\frac{\partial f}{\partial z}(x_{0}+h_{1}t,y_{0}+h_{2}t,z_{0}+h_{3}t)\cdot \frac{d(z_{0}+h_{3}t)}{dt}=$$

$$\frac{\partial f}{\partial x}(x_{0}+h_{1}t,y_{0}+h_{2}t,z_{0}+h_{3})\cdot h_{1}+\frac{\partial f}{\partial y}(x_{0}+h_{1}t,y_{0}+h_{2}t,z_{0}+h_{3})\cdot h_{2}+\frac{\partial f}{\partial z}(x_{0}+h_{1}t,y_{0}+h_{2}t,z_{0}+h_{3})\cdot h_{3}$$

Vamos ahora a calcular $F^{´´}(t)$

$$F^{´´}(t)=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}h_{1}+ \frac{\partial f}{\partial y}h_{2}+\frac{\partial f}{\partial z}h_{3}\right)h_{1}+\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}h_{1}+ \frac{\partial f}{\partial y}h_{2}+\frac{\partial f}{\partial z}h_{3}\right)h_{2}+\frac{\partial}{\partial z}\left(\frac{\partial f}{\partial x}h_{1}+ \frac{\partial f}{\partial y}h_{2}+\frac{\partial f}{\partial z}h_{3}\right)h_{3}=$$

$$\frac{\partial^{2}f}{\partial x^{2}}h_{1}^{2}+2\frac{\partial^{2}f}{\partial x\partial y}h_{1}h_{2}+\frac{\partial^{2}f}{\partial y^{2}}h_{2}^{2}+2\frac{\partial^{2}f}{\partial x\partial z}h_{3}h_{1}+2\frac{\partial^{2}f}{\partial y\partial z}h_{3}h_{2}+\frac{\partial^{2}f}{\partial z^{2}}h_{3}^{2}$$
Ahora bien si se aplica la fórmula de Taylor con la forma del residuo de Lagrange a la función $$F(t)=f(x_{0}+h_{1}t,y_{0}+h_{2}t)$$ y ponemos $t=0$, y $n=2$ se tiene

$$F(t)=F(0)+\frac{1}{1!}F'(0)t+\frac{1}{2!}F^{´´}(0)t^{2}+R_{2}$$

ahora bien con $t=1$, $x=x_{0}+h_{1}$, $y=y_{0}+h_{2}$, $z=z_{0}+h_{3}$

$$f(x,y)=f(x_{0},y_{0})+\textcolor{Blue}{\left(\frac{\partial f}{\partial
x}\right){p}(x-x_{0})+\left(\frac{\partial f}{\partial
y}\right){p}(y-y_{0})+\left(\frac{\partial f}{\partial
z}\right){p}(z-z_{0})}+$$

$$\textcolor{Red}{\frac{1}{2!}\left(\frac{\partial^{2}f}{\partial
x^{2}}{p}(x-x_{0})^{2}+2\frac{\partial^{2}f}{\partial x \partial
y}{p}(x-x_{0})(y-y_{0})+\frac{\partial^{2}f}{\partial
y^{2}}{p}(y-y_{0})^{2}+2\frac{\partial^{2}f}{\partial
x\partial z}{p}(z-z_{0})(x-x_{0})+2\frac{\partial^{2}f}{\partial
y\partial z}{p}(z-z_{0})(y-y_{0})\right)}$$

$$\textcolor{Red}{+\frac{\partial^{2}f}{\partial
z^{2}}{p}(z-z_{0})}+R_{2}$$
Donde la expresión en azul se puede escribir

$$\textcolor{Blue}{\left(\frac{\partial f}{\partial
x}\right){p}(x-x_{0})+\left(\frac{\partial f}{\partial
y}\right){p}(y-y_{0})+\left(\frac{\partial f}{\partial
z}\right){p}(z-z_{0})=\nabla f(x_{0},y_{0},z_{0})\cdot (h_{1},h_{2},h_{3})}$$

y la expresión en rojo
$$\textcolor{Red}{\frac{1}{2!}\left(\frac{\partial^{2}f}{\partial x^{2}}h_{1}^{2}+2\frac{\partial^{2}f}{\partial x\partial y}h_{1}h_{2}+\frac{\partial^{2}f}{\partial y^{2}}h_{2}^{2}+2\frac{\partial^{2}f}{\partial x\partial z}h_{3}h_{1}+2\frac{\partial^{2}f}{\partial y\partial z}h_{3}h_{2}+\frac{\partial^{2}f}{\partial z^{2}}h_{3}^{2}\right)}$$

se puede ver como producto de matrices

$$\frac{1}{2!}(h_{1}~h_{2}~h_{3})\left(\begin{matrix}\frac{\partial^{2}f}{\partial
x^{2}}&\frac{\partial^{2}f}{\partial y \partial x}&\frac{\partial^{2}f}{\partial z \partial x}\\ \frac{\partial^{2}f}{\partial x \partial y}&\frac{\partial^{2}f}{\partial
y^{2}}&\frac{\partial^{2}f}{\partial z \partial y}\\ \frac{\partial^{2}f}{\partial
x \partial z}&\frac{\partial^{2}f}{\partial y \partial z}&\frac{\partial^{2}f}{\partial
z^{2}}\end{matrix}\right)_{p}\left(\begin{matrix}h{1}\\h_{2}\\h_{3}\end{matrix}\right)$$

La matriz
$$\left(\begin{matrix}\frac{\partial^{2}f}{\partial
x^{2}}&\frac{\partial^{2}f}{\partial
y\partial x}&\frac{\partial^{2}f}{\partial
z\partial x}\\\frac{\partial^{2}f}{\partial
x \partial y}&\frac{\partial^{2}f}{\partial
y^{2}}&\frac{\partial^{2}f}{\partial
z \partial y}\\\frac{\partial^{2}f}{\partial
x \partial z}&\frac{\partial^{2}f}{\partial
y \partial z}&\frac{\partial^{2}f}{\partial
z^{2}}\end{matrix}\right)$$
se le conoce como matriz Hessiana y se le denota $H(x_{0},y_{0},z_{0})$, por lo que la aproximación de Taylor se puede escribir

$$f(x,y)=f(x_{0},y_{0})+\nabla f(x_{0},y_{0},z_{0})\cdot (h_{1},h_{2},h_{3})+\frac{1}{2!}(h_{1}~h_{2}~h_{3})H(x_{0},y_{0},z_{0})\left(\begin{matrix}h_{1}\\h_{2}\\h_{3}\end{matrix}\right)$$

$\textbf{Ejemplo}$ Considere la función $f(x,y)=e^{2x+3y}$
$f[(0,0)+(x,y)]=f(0,0) +\nabla f(0,0)\cdot(x,y)+\frac{1}{2}[xy]H(0,0)\left[\begin{array}{c} x\\y\end{array}\right]+r_2(x,y)$

donde $\displaystyle\lim _{(x,y)\rightarrow(0,0)} \displaystyle\frac{r(x,y)}{x^2+y^2}=0$

$\nabla f=\left(\displaystyle\frac{\partial f}{\partial x}, \displaystyle\frac{\partial f}{\partial y}\right)=(2e^{2x+3y},3e^{2x+3y})~~~~ \therefore \nabla f(0,0)=(2,3)$

$$
H(x,y)=\left[\begin{array}{cc}
\displaystyle\frac{\partial ^2f}{\partial x^2} & \displaystyle\frac{\partial ^2f}{\partial y\partial x}\\
\displaystyle\frac{\partial ^2f}{\partial x\partial y} & \displaystyle\frac{\partial ^2f}{\partial y^2}\end{array}\right]=
\left[\begin{array}{cc}
4e^{2x+3} & 6e^{2x+3y}\\
6e^{2x+3y} & 9e^{2x+3y}\end{array}\right] ~~~~ \therefore H(0,0)= \left(\begin{array}{cc} 4&6\\6&9\end{array}\right)
$$

Así

Así $f(x,y)=f(0,0)+(2,3)\cdot (x,y) +\frac{1}{2}[xy]\left(\begin{array}{cc} 4&6\\6&9 \end{array}\right)\left[\begin{array}{c} x\\y\end{array}\right]+r(x,y)$
$\therefore e^{2x+3y}=1+2x+3y+2x^2+6xy\frac{9}{2}y^2+r(x,y)$

$\textcolor{Red}{\textbf{Extremos Locales}}$

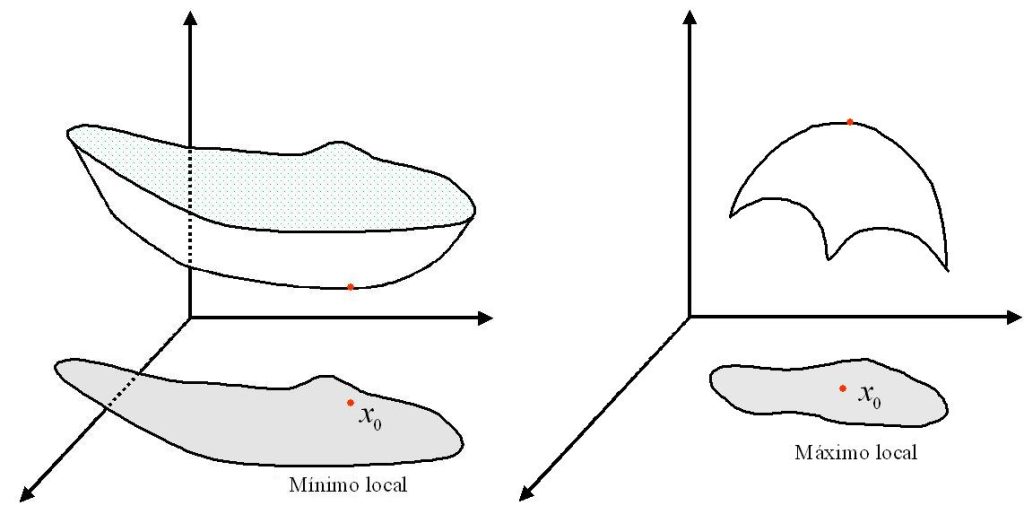
Entre las caracteristicas geometricas básicas de la gráficas de una función estan sus puntos extremos, en los cuales la función alcanza sus valores mayor y menor.

$\textbf{Definición 1.}$ Si $f:u\subset \mathbb{R}^n \rightarrow
\mathbb{R}$ es una función escalar, dado un punto $x_0 \in u$
se llama mínimo local de $f$ si existe una vecindad $v$ de $x_0$ tal que $\forall x \in v$ ,$f(x)>f(x_0)$. De manera analoga, $x_0 \in u$ es un máximo local si existe una vecindad $v$ de $x_0$ tal que $f(x)<f(x_0)$, $\forall \quad x \in v$. El punto $x_0 \in u$ es un extremo local o relativo, si es un mínimo local o máximo
local.

En la expresión del desarrollo de Taylor
$$f(x,y)=f(x_{0},y_{0})+\nabla f(x_{0},y_{0},z_{0})\cdot (h_{1},h_{2},h_{3})+\frac{1}{2!}(x-x_{0}\quad y-y_{0})(H(x_{0},y_{0}))\left(\begin{array}{c}
x-x_{0} \\y-y_{0} \end{array}\right)$$
Si consideramos los valores para los cuales

$$\nabla f(x_{0},y_{0},z_{0})=(0,0,0)$$
es decir los puntos críticos del gradiente entonces nuestra aproximación de Taylor nos queda

$$f(x,y)=f(x_{0},y_{0})+\frac{1}{2!}(x-x_{0}\quad y-y_{0})(H(x_{0},y_{0}))\left(\begin{array}{c}
x-x_{0} \\y-y_{0} \end{array}\right)$$
que se puede escribir
$$f(x,y)-f(x_{0},y_{0})=\frac{1}{2!}(x-x_{0}\quad y-y_{0})(H(x_{0},y_{0}))\left(\begin{array}{c}
x-x_{0} \\y-y_{0} \end{array}\right)$$

por lo que el signo del lado izquierdo $f(x,y)-f(x_{0},y_{0})$ dependerá del signo de la expresión
$$\frac{1}{2!}(x-x_{0}\quad y-y_{0})(H(x_{0},y_{0}))\left(\begin{array}{c}
x-x_{0} \\y-y_{0} \end{array}\right)$$

es decir dependerá del signo de la forma
$$\frac{1}{2!}(h_{1}~h_{2})\left(\begin{matrix}\frac{\partial^{2}f}{\partial
x^{2}}&\frac{\partial^{2}f}{\partial
y\partial x}\\\frac{\partial^{2}f}{\partial
x\partial y}&\frac{\partial^{2}f}{\partial
y^{2}}\end{matrix}\right)_{p}\left(\begin{matrix}h{1}\\h_{2}\\h_{3}\end{matrix}\right)$$

$\textbf{Teorema 1.}$ Sea $B=\left[\begin{array}{cc}
a & b \\
b & c \\
\end{array}
\right]$ y $H(h)=\frac{1}{2}[h_1,h_2]\left[
\begin{array}{cc}
a & b \\
b & c \\
\end{array}
\right]\left(
\begin{array}{c}
h_1 \\
h_2
\end{array}
\right)$ entonces $H(h)$ es definida positiva si y solo si $a>0$ y $ac-b^2>0$

$\small{Demostración.}$ Tenemos $$H(h)=\frac{1}{2}[h_1,h_2]\left[
\begin{array}{cc}
a h_1& bh_2 \\
b h_1& ch_2 \
\end{array}
\right]=\frac{1}{2}(ah_1^2+2bh_1h_2+ch_1^2)$$
si completamos el cuadrado
$$H(h)=\frac{1}{2}a\left(h_1+\frac{b}{a}h_2\right)^2+\frac{1}{2}\left(c-\frac{b^2}{a}\right)h_2^2$$
supongamos que $h$ es definida positiva. Haciendo
$h_2=0$ vemos que $a>0$. Haciendo $h_1=-\frac{b}{a}h_2$ $c-\frac{b^2}{a}>0$ ó $ac-b^2>0$. De manera analoga $H(h)$ es definida negativa si y solo si $a<0$ y $ac-b^2>0$. $\square$

Criterio del máximo y del mínimo para funciones de dos variables Sea $f(x,y)$ de clase
$C^3$ en un conjunto abierto $u$ de $\mathbb{R}^2$. Un punto $x_0,y_0$ es un mínimo local (Estricto) de $f$ si se cumple las siguientes tres condiciones:

$I)$ $\frac{\partial f}{\partial x}(x_0,y_0)=\frac{\partial f}{\partial y}(x_0,y_0)$
$II)$$\frac{\partial^2 f}{\partial x^2}(x_0,y_0)> 0$
$III)$ $\left(\frac{\partial^2 f}{\partial x^2}\right)\left(\frac{\partial^2 f}{\partial y^2}\right)-\left(\frac{\partial^2 f}{\partial x \partial y}\right)^2> 0$ en $(x_0,y_0)$ (Discriminante). Si en II) tenemos $<0$ en lugar de $>0$ sin cambiar III)
hay un máximo local.

Introducción

Este apartado considera algunos casos reales en los que podemos aplicar los conocimientos adquiridos a lo largo de éstas notas. Son ejemplos que nos permiten conocer que tipo de inversiones nos convienen más, como lo es cuando queremos invertir en CETES, ante dicha situación podemos usar el conocimiento adquirido para determinar, el valor de uno de sus títulos, y poner en práctica de forma real, para conocer mejor cual es el manejo real de algunas una de las formulas, evidenciando la forma en la que se pueden utilizar de forma aplicada en alguna situación real.

Aplicación en CETES

Como se estuvo exponiendo a lo largo del desarrollo de éstas notas, las matemáticas financieras son una poderosa herramienta, que nos sirve para determinar el valor del dinero a través del tiempo. Para realizar dicho análisis, vimos una cierta cantidad de conceptos que nos permitieron comprender mejor cómo funciona el mundo de las finanzas, aspectos que la afectan como lo es la inflación, partiendo desde el ejemplo más simple de interés compuesto, hasta llegar al punto de elaborar tablas de amortización, calculo de valor de bonos, temas en los que se combinaban una enorme cantidad de conceptos para su construcción.

En este apartado, lo que se va a realizar es, mostrar algunos ejemplos con aplicaciones reales, de los conceptos que en éstas notas se estuvieron abordando, para que se pueda tener una mejor comprensión de la importancia del uso de las matemáticas financieras, en el mundo real.

Un ejemplo práctico del uso de las matemáticas financieras, en un caso real es el siguiente:

El precio de un CETE se puede calcular, conociendo su tasa de rendimiento, o su tasa de descuento, y se obtiene utilizando la siguiente ecuación*:

$$P=\frac{VN}{\left(1+\frac{i*t}{360}\right)}$$

donde:

P = Valor del CETE (redondeado a 7 decimales)

VN = Valor Nominal del título en pesos

i = Tasa de rendimiento

t = tiempo o plazo en días del CETE

Si $d$ es la tasa de descuento de un CETE se tiene que:

$$d=\frac{i}{\left(1+\frac{i*t}{360}\right)}$$

despejando $i$,

$$i=\frac{d}{\left(1-\frac{d*t}{360}\right)}$$

Al sustituir éste resultado en la primer ecuación se obtiene el precio de un CETE a partir de su tasa de descuento:

$$P=VN*\left(1-\frac{d*t}{360}\right)$$

Por lo que se tiene que el precio de un CETE está compuesto por el valor presente de su valor nominal.

Ejercicios resueltos

Ejercicio. El 31 de agosto del año 2000, un inversionista compra CETES con las siguientes características:

• Valor nominal: \$10 pesos
• Fecha de colocación: 31 de agosto del año 2020
• Fecha de vencimiento: 28 de septiembre del año 2020
• Días por vencer del título: 28 días

Suponiendo que está sujeto a una tasa de rendimiento anual del 15%, obtener el valor del CETE.

Ejercicio. Supongamos ahora, el siguiente caso: un inversionista compra CETES con las siguientes características:

• Valor nominal: \$10 pesos
• Fecha de colocación: 24 de Marzo de 2023
• Fecha de vencimiento: 23 de junio de 2023
• Duración del título: 91 días
• Tasa de rendimiento: 4.39%

*Información obtenida de https://www.banxico.org.mx/mercados/d/%7B0DE0044F-662D-09D2-C8B3-4F1A8E43655F%7D.pdf

**información obtenida de: https://www.banxico.org.mx/elib/mercado-valores-gub-en/OEBPS/Rsc/anexo0201.pdf

• Ir a Matemáticas Financieras
• Entrada anterior
• Entrada siguiente

$\textcolor{Red}{\textbf{Diferencial de orden n}}$

$$d^{n}f=\frac{\partial^{n} f}{\partial x^{n}}dx^{n}+\left(\begin{matrix}n\\1\end{matrix}\right)\frac{\partial^{n-1} f}{\partial x^{n-1}\partial y}dx^{n-1}dy+\left(\begin{matrix}n\\2\end{matrix}\right)\frac{\partial^{n-2} f}{\partial x^{n-2}\partial y^{2}}dx^{n-2}dy^{2}+\cdots+$$ $$\left(\begin{matrix}n\\k\end{matrix}\right)\frac{\partial^{n-k} f}{\partial x^{n-k}\partial y^{k}}dx^{n-k}dy^{k}+\cdots+\frac{\partial^{n}f}{\partial y^{n}}dy^{n}$$
que se puede escribir
$$d^{n}f=\sum_{j=0}^{n}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n}f}{\partial x^{n-j}\partial y^{j}}dx^{n-j}dy^{j}$$

$\textbf{Ejercicio}$ Probar usando inducción
$$d^{n}f=\sum_{j=0}^{n}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n}f}{\partial x^{n-j}\partial y^{j}}dx^{n-j}dy^{j}$$

$\small{Solución.}$ Para n=1 se tiene
$$df=\frac{\partial f}{\partial x}dx+\frac{\partial f}{\partial y}dy$$
Suponemos valido para n

$$d^{n}f=\sum_{j=0}^{n}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n}f}{\partial x^{n-j}\partial y^{j}}dx^{n-j}dy^{j}$$
Por demostrar que es valida para n+1
$$d^{n+1}f=d(d^{n}f)=\frac{\partial}{\partial x}\left(\sum_{j=0}^{n}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n}f}{\partial x^{n-j}\partial y^{j}}dx^{n-j}dy^{j}\right)dx+\frac{\partial}{\partial y}\left(\sum_{j=0}^{n}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n}f}{\partial x^{n-j}\partial y^{j}}dx^{n-j}dy^{j}\right)dy=$$

$$\sum_{j=0}^{n}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n+1}f}{\partial x^{n+1-j}\partial y^{j}}dx^{n+1-j}dy^{j}+\sum_{j=0}^{n}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n+1}f}{\partial x^{n-j}\partial y^{j+1}}dx^{n-j}dy^{j+1}=$$
$$\sum_{j=0}^{n}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n+1}f}{\partial x^{n+1-j}\partial y^{j}}dx^{n+1-j}dy^{j}+\sum_{j=1}^{n+1}\left(\begin{matrix}n\\j-1\end{matrix}\right)\frac{\partial^{n+1}f}{\partial x^{n+1-j}\partial y^{j}}dx^{n+1-j}dy^{j}=$$

$$\frac{\partial^{n+1}f}{\partial x^{n+1}}dx^{n+1}+\sum_{j=1}^{n}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n+1}f}{\partial x^{n+1-j}\partial y^{j}}dx^{n+1-j}dy^{j}+\sum_{j=1}^{n}\left(\begin{matrix}n\\j-1\end{matrix}\right)\frac{\partial^{n+1}f}{\partial x^{n+1-j}\partial y^{j}}dx^{n+1-j}dy^{j}+\frac{\partial^{n+1}f}{\partial y^{n+1}}dy^{n+1}=$$

$$\frac{\partial^{n+1}f}{\partial x^{n+1}}dx^{n+1}+\sum_{j=1}^{n}\left(\left(\begin{matrix}n\\j\end{matrix}\right)+\left(\begin{matrix}n\\j-1\end{matrix}\right)\right)\frac{\partial^{n+1}f}{\partial x^{n+1-j}\partial y^{j}}dx^{n+1-j}dy^{j}+\frac{\partial^{n+1}f}{\partial y^{n+1}}dy^{n+1}=$$

$$\frac{\partial^{n+1}f}{\partial x^{n+1}}dx^{n+1}+\sum_{j=1}^{n}\left(\begin{matrix}n+1\\j\end{matrix}\right)\frac{\partial^{n+1}f}{\partial x^{n+1-j}\partial y^{j}}dx^{n+1-j}dy^{j}+\frac{\partial^{n+1}f}{\partial y^{n+1}}dy^{n+1}=\sum_{j=0}^{n+1}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n}f}{\partial x^{n-j}\partial y^{j}}dx^{n-j}dy^{j}$$

La última fórmula puede expresarse simbólicamente por la ecuación
$$d^{n}f=\left(\frac{\partial}{\partial x}dx+\frac{\partial}{\partial y}dy\right)^{n}f$$

donde primero debe desarrollarse le expresión de la derecha formalmente por medio del teorema del binomio y, a continuación deben sustituirse los términos
$$\frac{\partial^{n}f}{\partial x^{n}}dx^{n},\frac{\partial^{n}f}{\partial x^{n-1}\partial y}dx^{n-1}dy,\cdots,\frac{\partial^{n}f}{\partial y^{n}}dy^{n}$$
por los términos
$$\left(\frac{\partial}{\partial x}dx\right)^{n}f,\left(\frac{\partial}{\partial x}dx\right)^{n-1}\left(\frac{\partial}{\partial y}dy\right)f,\cdots,\left(\frac{\partial}{\partial y}dy\right)^{n}f$$

$\textcolor{Red}{\textbf{Teorema de Taylor para funciones $f:A\subset\mathbb{R}^{2}\rightarrow\mathbb{R}$}}$

Recordando el $\textcolor{Red}{\text{Teorema de Taylor para funciones $f:\mathbb{R}\rightarrow\mathbb{R}$}}$

$\textbf{Teorema.-}$ Si $f(x)$ tiene n-ésima derivada continua en una vecindad de $x_{0}$, entonces en esa vecindad
$$f(x)=f(x_{0})+\frac{1}{1!}f'(x_{0})(x-x_{0})+\frac{1}{2!}f»(x_{0})(x-x_{0})^{2}+\frac{1}{3!}f»'(x_{0})(x-x_{0})^{3}+…+\frac{1}{n!}f^{n}(x_{0})(x-x_{0})^{n}+R_{n}$$
donde
$$R_{n}=\frac{f^{n+1}(\epsilon)}{(n+1)!}(x-x_{0})^{n+1},~donde~\epsilon\in(x_{0},x)$$

Sea $f:A\subset\mathbb{R}^{2}\rightarrow\mathbb{R}$ y sea $F(t)=f(x_{0}+h_{1}t,y_{0}+h_{2}t)$ con $t\in[0,1]$, de esta manera f recorre el segmento de $[x_{0},y_{0}]$ a $[x_{0}+h_{1}t,y_{0}+h_{2}t]$. Se tiene entonces que usando la regla de la cadena
$$F'(t)=\frac{\partial f}{\partial x}(x_{0}+h_{1}t,y_{0}+h_{2}t)\cdot \frac{d(x_{0}+h_{1}t)}{dt}+\frac{\partial f}{\partial y}(x_{0}+h_{1}t,y_{0}+h_{2}t)\cdot \frac{d(y_{0}+h_{2}t)}{dt}=$$

$$\frac{\partial f}{\partial x}(x_{0}+h_{1}t,y_{0}+h_{2}t)\cdot h_{1}+\frac{\partial f}{\partial y}(x_{0}+h_{1}t,y_{0}+h_{2}t)\cdot h_{2}$$
Vamos ahora a calcular $F^{´´}(t)$

$$F^{´´} ( t )=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}h_{1}+ \frac{\partial f}{\partial y}h_{2}\right)h_{1}+\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}h_{1}+ \frac{\partial f}{\partial y}h_{2}\right)h_{2}=$$
$$\frac{\partial^{2} f}{\partial x^{2}}h_{1}^{2}+2\frac{\partial^{2} f}{\partial x\partial y}h_{1}h_{2}+\frac{\partial^{2} f}{\partial y^{2}}h_{2}^{2}$$

simbólicamente se puede escribir
$$F^{»}(t)=\left(\frac{\partial }{\partial x}\cdot h_{1}+\frac{\partial }{\partial y}\cdot h_{2}\right)^{2}f$$
y en general

$$F^{n}(t)=\frac{\partial^{n} f}{\partial x^{n}}h_{1}^{n}+\left(\begin{matrix}n\\1\end{matrix}\right)\frac{\partial^{n-1} f}{\partial x^{n-1}\partial y}h_{1}^{n-1}h_{2}+\left(\begin{matrix}n\\2\end{matrix}\right)\frac{\partial^{n-2} f}{\partial x^{n-2}\partial y^{2}}h_{1}^{n-2}h_{2}^{2}+\cdots+\left(\begin{matrix}n\\k\end{matrix}\right)\frac{\partial^{n-k} f}{\partial x^{n-k}\partial y^{k}}h_{1}^{n-k}h_{2}^{k}+\cdots+\frac{\partial^{n}f}{\partial y^{n}}h_{2}^{n}$$

que simbólicamente se puede escribir
$$F^{n}=\sum_{j=0}^{n}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n}f}{\partial x^{n-j}\partial y^{j}}h_{1}^{n-j}h_{2}^{j}=\left(\frac{\partial }{\partial x}\cdot h_{1}+\frac{\partial }{\partial y}\cdot h_{2}\right)^{n}f$$

Ahora bien si se aplica la fórmula de Taylor con la forma del residuo de Lagrange a la función $$F(t)=f(x_{0}+h_{1}t,y_{0}+h_{2}t)$$ y ponemos $t=0$, se tiene
$$F(t)=F(0)+\frac{1}{1!}F'(0)t+\frac{1}{2!}F^{»}(0)t^{2}+\frac{1}{3!}F»'(0)t^{3}+…++\frac{1}{n!}F^{^{n}}(0)t^{n}+R_{n}$$
ahora bien con $t=1$
$$f(x_{0}+h_{1},y_{0}+h_{2})=f(x_{0},y_{0})+\frac{1}{1!}\left(\frac{\partial f}{\partial x}(x_{0},y_{0})\cdot h_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})\cdot h_{2}\right)+\frac{1}{2!}\left(\frac{\partial^{2} f}{\partial x^{2}}(x_{0},y_{0})h_{1}^{2}+2\frac{\partial^{2} f}{\partial x\partial y}(x_{0},y_{0})h_{1}h_{2}+\frac{\partial^{2} f}{\partial y^{2}}(x_{0},y_{0})h_{2}^{2}\right)$$
$$+\cdots+\frac{1}{n!}\left(\sum_{j=0}^{n+1}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n}f}{\partial x^{n-j}\partial y^{j}}(x_{0},y_{0})h_{1}^{n-j}h_{2}^{j}\right)$$

$x=x_{0}+h_{1}$, $y_{0}+h_{2}=y$ por lo que $h_{1}=x-x_{0}$ y $h_{2}=y-y_{0}$ entonces

$$f(x,y)=f(x_{0},y_{0})+\frac{1}{1!}\left(\frac{\partial f}{\partial x}(x_{0},y_{0})\cdot (x-x_{0})+\frac{\partial f}{\partial y}(x_{0},y_{0})\cdot (y-y_{0})\right)+$$

$$\frac{1}{2!}\left(\frac{\partial^{2} f}{\partial x^{2}}(x_{0},y_{0})(x-x_{0})^{2}+2\frac{\partial^{2} f}{\partial x\partial y}(x_{0},y_{0})(x-x_{0})(y-y_{0})+\frac{\partial^{2} f}{\partial y^{2}}(x_{0},y_{0})(y-y_{0})^{2}\right)+$$

$$\cdots+\frac{1}{n!}\left(\sum_{j=0}^{n+1}\left(\begin{matrix}n\\j\end{matrix}\right)\frac{\partial^{n}f}{\partial x^{n-j}\partial y^{j}}(x_{0},y_{0})(x-x_{0})^{n-j}(y-y_{0})^{j}\right)+R_{n}$$

donde
$$R_{n}=\frac{1}{n+1!}\left((x-x_{0})^{n+1}\frac{\partial^{n+1}f}{\partial x^{n+1}}(\xi,\eta)+\cdots+(y-y_{0})^{n+1}\frac{\partial^{n+1}f}{\partial y^{n+1}}(\xi,\eta)\right)$$ donde $\xi\in(x_{0},x_{0}+h_{1})$ y $\eta\in(y_{0},y_{0}+h_{2})$\En general el residuo $R_{n}$ se anula en un orden mayor que el término $d^{n}f$

$\textbf{Ejemplo}$ Desarrollar la fórmula de Taylor en $(x_{0},y_{0})=(0,0)$ con $n=3$ para la función $$f(x,y)=e^{y}\cos x$$

$\small{Solución.}$

En este caso tenemos que
$$f(0,0)=e^{0}\cos(0)=1$$
Para la diferencial de orden 1
$$\frac{\partial f}{\partial x}(0,0)~\Rightarrow~\frac{\partial (e^{y}\cos(x))}{\partial x}(0,0)~\Rightarrow~-e^{y} sen\left( x\right) \big{|}{(0,0)}=0$$ $$\frac{\partial f}{\partial y}(0,0)~\Rightarrow~\frac{\partial (e^{y} \cos x)}{\partial y}(0,0)~\Rightarrow~-e^{y}\cos(x)\big{|}{(0,0)}=1$$
por lo tanto
$$\frac{1}{1!}\left(\frac{\partial f}{\partial x}(x_{0},y_{0})\cdot (x-x_{0})+\frac{\partial f}{\partial y}(x_{0},y_{0})\cdot (y-y_{0})\right)=\frac{1}{1!}\left((0)(x)+(1)(y)\right)=y$$
Para la diferencial de orden 2
$$\frac{\partial^{2} f}{\partial x^{2}}(x_{0},y_{0})~\Rightarrow~\frac{\partial^{2} (e^{y}\ cos x)}{\partial x^{2}}(0,0)~\Rightarrow~-e^{y} \cos~x\big{|}{(0,0)}=-1$$ $$\frac{\partial^{2} f}{\partial y^{2}}(x{0},y_{0})~\Rightarrow~\frac{\partial^{2} (e^{y} \cos x)}{\partial y^{2}}(0,0)~\Rightarrow~e^{y} \cos~x\big{|}{(0,0)}=1$$ $$\frac{\partial^{2} f}{\partial x~\partial y}(x{0},y_{0})~\Rightarrow~\frac{\partial^{2} (e^{y}\cos x)}{\partial x~\partial y}(0,0)~\Rightarrow~-e^{y} sen~x~ \big{|}{(0,0)}=0$$ Por lo tanto $$\frac{1}{2!}\left(\frac{\partial^{2} f}{\partial x^{2}}(x{0},y_{0})h_{1}^{2}+2\frac{\partial^{2} f}{\partial x\partial y}(x_{0},y_{0})h_{1}h_{2}+\frac{\partial^{2} f}{\partial y^{2}}(x_{0},y_{0})h_{2}^{2}\right)=\frac{1}{2!}((-1)x^{2}+2(0)xy+(1)y^{2})$$
Para la diferencial de orden 3

$$\frac{\partial^{3} f}{\partial x^{3}}(x_{0},y_{0})~\Rightarrow~e^{y} sen~x\big{|}_{(0,0)}=0$$

$$\frac{\partial^{3} f}{\partial y^{3}}(x_{0},y_{0})~\Rightarrow~\frac{\partial^{2} (e^{y}\cos x)}{\partial y^{3}}(0,0)~\Rightarrow~e^{y}\cos~x\big{|}_{(0,0)}=1$$

$$\frac{\partial^{3} f}{\partial x^{2}~\partial y}(x_{0},y_{0})~\Rightarrow~\frac{\partial^{2} (e^{y}\cos x)}{\partial x^{2}~\partial y}(0,0)~\Rightarrow~-e^{y}\cos~x\big{|}_{(0,0)}=-1$$

$$\frac{\partial^{3} f}{\partial y^{3}}(x_{0},y_{0})~\Rightarrow~\frac{\partial^{2} (e^{y}\cos x)}{\partial y^{3}}(0,0)~\Rightarrow~e^{y}\cos~x\big{|}_{(0,0)}=1$$

$$\frac{\partial^{3} f}{\partial x~\partial y^{2}}(x_{0},y_{0})~\Rightarrow~\frac{\partial^{2} (e^{y}\cos x)}{\partial x~\partial y^{2}}(0,0)~\Rightarrow~-e^{y} sen~x\big{|}_{(0,0)}=0$$

Por lo tanto
$$\frac{1}{3!}\left(\frac{\partial^{3} f}{\partial x^{3}}h_{1}^{3}+3\frac{\partial^{3} f}{\partial x^{2}\partial y}h_{}1^{2}h_{2}+3\frac{\partial^{3} f}{\partial x\partial y^{2}}h_{1}h_{2}^{2}+\frac{\partial^{3} f}{\partial y^{3}}h_{}2^{3}\right)=$$

$$\frac{1}{3!}\left((0)(x^{3})+3(-1)x^{2}y+3(0)xy^{2}+(1)y^{3}\right)$$
Finalmente para el residuo se tiene

$$\frac{\partial^{4} f}{\partial x^{4}}(x_{0},y_{0})~\Rightarrow~\frac{\partial^{4} (e^{y}\cos(x))}{\partial y^{3}}(0,0)~\Rightarrow~e^{y}\cos~x\big{|}_{(\xi,\eta)}=e^{\eta}\cos~\xi$$

$$\frac{\partial^{4} f}{\partial x^{2}\partial y^{2}}(x_{0},y_{0})~\Rightarrow~\frac{\partial^{4} (e^{y}\cos x)}{\partial x^{2}\partial y^{2}}(0,0)~\Rightarrow~-e^{y}\cos~x\big{|}_{(\xi,\eta)}=-e^{\eta}\cos~\xi$$

$$\frac{\partial^{4} f}{\partial x\partial y^{3}}(x_{0},y_{0})~\Rightarrow~\frac{\partial^{4} (e^{y}\cos x)}{\partial x\partial y^{3}}(0,0)~\Rightarrow~-e^{y} sen~x\big{|}_{(\xi,\eta)}=-e^{\eta} sen~\xi$$

$$\frac{\partial^{4} f}{\partial y^{4}}(x_{0},y_{0})~\Rightarrow~\frac{\partial^{4} (e^{y}\cos x)}{\partial y^{4}}(0,0)~\Rightarrow~e^{y}\cos~x\big{|}_{(\xi,\eta)}=e^{\eta}\cos~\xi$$

$$R_{3}=\frac{1}{4!}\left(\frac{\partial^{4} f}{\partial x^{4}}h_{1}^{4}+4\frac{\partial^{4} f}{\partial x^{3}\partial y}h_{1}^{3}h_{2}+6\frac{\partial^{4} f}{\partial x^{2}\partial y^{2}}h_{1}^{2}h_{2}^{2}+4\frac{\partial^{4} f}{\partial x\partial y^{3}}h_{1}h_{2}^{3}+\frac{\partial^{4} f}{\partial h_{2}^{4}}dy^{4}\right)$$

$$=\frac{1}{4!}\left(x^{4}e^{\eta}\cos~\xi+4x^{3}ye^{\eta} sen~xi-6x^{2}y^{2}e^{\eta}\cos~\xi-4xy^{3}e^{\eta} sen~\xi+y^{4}e^{\eta}\cos~\xi\right)$$

Por lo que nuestro desarrollo de Taylor nos queda
$$e^{y}\cos~x=1+y+\frac{1}{2}(x^{2}-y^{2})+\frac{1}{6}(x^{3}-3xy^{2})+R_{3}$$
donde
$$R_{3}=\frac{1}{4!}\left(x^{4}e^{\eta}\cos~\xi+4x^{3}ye^{\eta} sen~xi-6x^{2}y^{2}e^{\eta}\cos~\xi-4xy^{3}e^{\eta} sen~\xi+y^{4}e^{\eta}\cos~\xi\right)$$
$\textbf{Ejercicio}$ Use la fórmula de Taylor en
$$f(x,y)=\cos~(x+y)$$
en el punto $(x_{0},y_{0})=(0,0)$ con $n=2$ para comprobar que
$$\lim_{(x,y)\rightarrow(0,0)}\frac{1-\cos~(x+y)}{(x^{2}+y^{2})^{2}}=\frac{1}{2}$$

En este caso para
$$f(x,y)=\cos(x+y)$$
se tiene
$$f(0,0)=\cos(0+0)=1$$
Para la diferencial de orden 1
$$\frac{\partial f}{\partial x}(0,0)~\Rightarrow~\frac{\partial (\cos x+y)}{\partial x}(0,0)~\Rightarrow~- sen(x+y)\big{|}{(0,0)}=0$$ $$\frac{\partial f}{\partial y}(0,0)~\Rightarrow~\frac{\partial (\cos x+y)}{\partial y}(0,0)~\Rightarrow~- sen(x+y)\big{|}{(0,0)}=0$$
por lo tanto

$$\frac{1}{1!}\left(\frac{\partial f}{\partial x}(x_{0},y_{0})\cdot (x-x_{0})+\frac{\partial f}{\partial y}(x_{0},y_{0})\cdot (y-y_{0})\right)=\frac{1}{1!}\left((0)(x)+(0)(y)\right)=0$$

Para la diferencial de orden 2
$$\frac{\partial^{2} f}{\partial x^{2}}(x_{0},y_{0})~\Rightarrow~\frac{\partial^{2} (\cos x+y)}{\partial x^{2}}(0,0)~\Rightarrow~-\cos~x+y\big{|}{(0,0)}=-1$$ $$\frac{\partial^{2} f}{\partial y^{2}}(x{0},y_{0})~\Rightarrow~\frac{\partial^{2} (\cos x+y)}{\partial y^{2}}(0,0)~\Rightarrow~-\cos~x+y\big{|}{(0,0)}=-1$$ $$\frac{\partial^{2} f}{\partial x~\partial y}(x{0},y_{0})~\Rightarrow~\frac{\partial^{2} (\cos x+y)}{\partial x~\partial y}(0,0)~\Rightarrow~-\cos~x+y\big{|}_{(0,0)}=-1$$
Por lo tanto

$$\frac{1}{2!}\left(\frac{\partial^{2} f}{\partial x^{2}}(x_{0},y_{0})h_{1}^{2}+2\frac{\partial^{2} f}{\partial x\partial y}(x_{0},y_{0})h_{1}h_{2}+\frac{\partial^{2} f}{\partial y^{2}}(x_{0},y_{0})h_{2}^{2}\right)=\frac{1}{2!}((-1)x^{2}-2xy+(-1)y^{2})$$
Por lo que nuestro desarrollo de Taylor nos queda
$$\cos(x+y)=1-\frac{x^{2}}{2}-xy-\frac{y^{2}}{2}$$
De manera que

$$\lim_{(x,y)\rightarrow(0,0)}\frac{1-\cos~(x+y)}{(x^{2}+y^{2})^{2}}=\lim_{(x,y)\rightarrow(0,0)}\frac{1-(1-\frac{x^{2}}{2}-xy-\frac{y^{2}}{2})}{(x^{2}+y^{2})^{2}}$$
$$=\lim_{(x,y)\rightarrow(0,0)}\frac{1}{2}\frac{(x^{2}+y^{2})^{2}}{(x^{2}+y^{2})^{2}}=\frac{1}{2}$$

$\textcolor{Red}{\textbf{Derivadas Parciales de Orden Superior}}$

Si $f$ es una función de doas variables $x,y$ $\Rightarrow$ $\displaystyle\frac{\partial f}{\partial x}, \displaystyle\frac{\partial f}{\partial y}$ son funciones de las mismas variables, cuando derivamos $\displaystyle\frac{\partial f}{\partial x}$ y $ \displaystyle\frac{\partial f}{\partial y}$ obtenemos las derivadas parciales de segundo orden, las derivadas de $\displaystyle\frac{\partial f}{\partial x}$ están definidas por:

$$\displaystyle\frac{\partial^{2}f}{\partial x^{2}}(x,y)=\displaystyle\lim_{h\to 0}{\displaystyle\frac{\displaystyle\frac{\partial f}{\partial x}(x+h,y)-\displaystyle\frac{\partial f}{\partial x}(x,y)}{h}}$$

$$\displaystyle\frac{\partial^{2}f}{\partial y \partial x}(x,y)=\displaystyle\lim_{k\to 0}{\displaystyle\frac{\displaystyle\frac{\partial f}{\partial x}(x,y+k)-\displaystyle\frac{\partial f}{\partial x}(x,y)}{k}}$$

Si $f$ es una función de dos variables entonces hay cuatro derivadas parciales de segundo orden.

Consideremos las diferentes notaciones para las derivadas parciales:

$$f_{1,1}=\displaystyle\frac{\partial^{2}f}{\partial x^{2}}=f_{xx}$$

$$f_{1,2}=\displaystyle\frac{\partial^{2}f}{\partial y \partial x}=\frac{\partial}{\partial y}\bigg(\frac{\partial f}{\partial x}\bigg)=f_{xy}$$

$$f_{2,1}=\displaystyle\frac{\partial^{2}f}{\partial x \partial y}=\frac{\partial}{\partial x}\bigg(\frac{\partial f}{\partial y}\bigg)=f_{yx}$$

$$f_{2,2}=\displaystyle\frac{\partial^{2}f}{\partial y^{2}}=\frac{\partial}{\partial y}\bigg(\frac{\partial f}{\partial y}\bigg)=f_{yy}$$

$\textbf{Ejemplo.}$ $z=x^{3}+3x^{2}y-2x^{2}y^{2}-y^{4}+3xy$ hallar $\displaystyle\frac{\partial z}{\partial x}, \displaystyle\frac{\partial z}{\partial y},\displaystyle\frac{\partial^{2} z}{\partial x^{2}},\displaystyle\frac{\partial^{2}z}{\partial x \partial y},\displaystyle\frac{\partial^{2}z}{\partial y \partial x},\displaystyle\frac{\partial^{2} z}{\partial y^{2}}$

$$\displaystyle\frac{\partial z}{\partial x}=3x^{2}+6xy-4xy^{2}+3y$$

$$\displaystyle\frac{\partial z}{\partial y}=3x^{2}-4x^{2}y-4y^{3}+3x$$

$$\displaystyle\frac{\partial^{2} z}{\partial x^{2}}=6x+6y-4y^{2}$$

$$\displaystyle\frac{\partial^{2} z}{\partial y^{2}}=-4x^{2}-12y^{2}$$

$$\displaystyle\frac{\partial^{2}z}{\partial y \partial x}=6x-8xy+3$$

$$\displaystyle\frac{\partial^{2}z}{\partial x \partial y}=6x-8xy+3$$

$\textbf{Teorema 1.}$ $\textcolor{Red}{\textbf{Teorema de schwarz}}$

Sea $f:A\subset \mathbb{R}^{2}\rightarrow\mathbb{R}$ una función definida en el abierto A de $\mathbb{R}^{2}$. Si las derivadas parciales

$$\frac{\partial^{2} f}{\partial y\partial x}~y~\frac{\partial^{2} f}{\partial x\partial y}$$

existen y son continuas en $A$, entonces

$$\frac{\partial^{2} f}{\partial y\partial x}=\frac{\partial^{2} f}{\partial x\partial y}$$

$\small{Demostración.}$ Sea

$\displaystyle{M=f(x+h_{1},y+h_{2})-f(x+h_{1},y)-f(x,y+h_{2})+f(x,y)}$ y definimos $$\varphi(x)=f(x,y+h_{2})-f(x,y)$$de manera que
$$\varphi(x+h_{1})-\varphi(x)=f(x+h_{1},y+h_{2})-f(x+h_{1},y)-(f(x,y+h_{2})-f(x,y))=M$$

Aplicando el TVM a $\varphi$ en el intervalo $[x,x+h_{1}]$ se tiene que existe $\theta~\in~(x,x+h_{1})$ tal que

$$\varphi(x+h_{1})-\varphi(x)=\varphi'(\theta)h_{1}$$

por otro lado
$$\varphi'(x)=\frac{\partial f}{\partial x}(x,y+h_{2})-\frac{\partial f}{\partial x}(x,y)$$
por lo tanto
$$\varphi'(\theta)=\frac{\partial f}{\partial x}(\theta,y+h_{2})-\frac{\partial f}{\partial x}(\theta,y)$$
tenemos entonces que

$$M=\varphi(x+h_{1})-\varphi(x)=\varphi'(\theta)h_{1}=\left(\frac{\partial f}{\partial x}(\theta,y+h_{2})-\frac{\partial f}{\partial x}(\theta,y)\right)h_{1}$$
Consideremos ahora $\displaystyle{\psi(y)=\frac{\partial f}{\partial x}(x,y)}$. Aplicando el TVM a $\psi$ en el intervalo $[y,y+h_{2}]$ se tiene que existe $\eta~\in~(y,y+h_{2})$ tal que
$$\psi(y+h_{2})-\psi(y)=\psi'(\eta)h_{2}$$
por otro lado

$$\psi'(y)=\frac{\partial }{\partial y}\left(\frac{\partial f}{\partial x}\right)(x,y)=\frac{\partial^{2}f}{\partial y\partial x}(x,y)$$
por lo tanto
$$\psi'(\eta)=\frac{\partial^{2}f}{\partial y\partial x}(x,\eta)$$
de esta manera

$$\psi(y+h_{2})-\psi(y)=\psi'(\eta)h_{2}=\left(\frac{\partial^{2}f}{\partial y\partial x}(x,\eta)\right)h_{2}$$
y si $\theta\in (x,x+h_{1})$ tenemos entonces que

$$\frac{\partial f}{\partial x}(\theta,y+h_{2})-\frac{\partial f}{\partial x}(\theta,y)=\left(\frac{\partial^{2}f}{\partial y\partial x}(\theta,\eta)\right)h_{2}$$
en consecuencia
$$M=\left(\frac{\partial f}{\partial x}(\theta,y+h_{2})-\frac{\partial f}{\partial x}(\theta,y)\right)h_{1}=\left(\frac{\partial^{2}f}{\partial y\partial x}(\theta,\eta)\right)h_{2}h_{1}$$

Consideremos ahora $$\overline{\varphi}(y)=f(x+h_{1},y)-f(x,y)$$de manera que
$$\overline{\varphi}(y+h_{2})-\overline{\varphi}(y)=f(x+h_{1},y+h_{2})-f(x+h_{1},y)-(f(x,y+h_{2})-f(x,y))=M$$

Aplicando el TVM a $\overline{\varphi}$ en el intervalo $[y,y+h_{2}]$ se tiene que existe $\overline{\eta}~\in~(y,y+h_{2})$ tal que
$$\overline{\varphi}(y+h_{2})-\overline{\varphi}(y)=\overline{\varphi}'(\overline{\eta})h_{2}$$
por otro lado
$$\overline{\varphi}'(y)=\frac{\partial f}{\partial y}(x+h_{1},y)-\frac{\partial f}{\partial y}(x,y)$$
por lo tanto

$$\overline{\varphi}'(\overline{\eta})=\frac{\partial f}{\partial y}(x+h_{1},\overline{\eta})-\frac{\partial f}{\partial y}(x,\overline{\eta})$$
tenemos entonces que
$$M=\overline{\varphi}(y+h_{2})-\overline{\varphi}(y)=\overline{\varphi}'(\overline{\eta})h_{2}=\left(\frac{\partial f}{\partial y}(x+h_{1},\overline{\eta})-\frac{\partial f}{\partial y}(x,\overline{\eta})\right)h_{2}$$

Consideremos ahora $\displaystyle{\overline{\psi}(x)=\frac{\partial f}{\partial y}(x,y)}$. Aplicando el TVM a $\psi$ en el intervalo $[x,x+h_{1}]$ se tiene que existe $\overline{\theta}~\in~(x,x+h_{1})$ tal que
$$\overline{\psi}(x+h_{1})-\overline{\psi}(x)=\overline{\psi}'(\overline{\theta})h_{1}$$
por otro lado

$$\overline{\psi}'(x)=\frac{\partial }{\partial x}\left(\frac{\partial f}{\partial y}\right)(x,y)=\frac{\partial^{2}f}{\partial x\partial y}(x,y)$$
por lo tanto
$$\overline{\psi}'(\overline{\theta})=\frac{\partial^{2}f}{\partial y\partial x}(\overline{\theta},y)$$
de esta manera

$$\overline{\psi}(x+h_{1})-\overline{\psi}(x)=\overline{\psi}'(\overline{\theta})h_{1}=\left(\frac{\partial^{2}f}{\partial x\partial y}(\overline{\theta},y)\right)h_{1}$$
es decir
$$\frac{\partial f}{\partial y}(x+h_{1},y)-\frac{\partial f}{\partial y}(x,y)=\left(\frac{\partial^{2}f}{\partial x\partial y}(\overline{\theta},y)\right)h_{1}$$
y si $\overline{\eta}\in (y,y+h_{2})$ tenemos entonces que
$$\frac{\partial f}{\partial y}(x+h_{1},\overline{\eta})-\frac{\partial f}{\partial y}(x,\overline{\eta})=\left(\frac{\partial^{2}f}{\partial x\partial y}(\overline{\theta},\overline{\eta})\right)h_{1}$$
en consecuencia

$$M=\left(\frac{\partial f}{\partial y}(x+h_{1},\overline{\eta})-\frac{\partial f}{\partial y}(x,\overline{\eta})\right)h_{1}h_{2}=\left(\frac{\partial^{2}f}{\partial x\partial y}(\overline{\theta},\overline{\eta})\right)h_{2}h_{1}$$
igualando ambas expresiones de M se tiene
$$\left(\frac{\partial^{2}f}{\partial y\partial x}(\theta,\eta)\right)h_{2}h_{1}=\left(\frac{\partial^{2}f}{\partial x\partial y}(\overline{\theta},\overline{\eta})\right)h_{2}h_{1}$$
donde
$$\left(\frac{\partial^{2}f}{\partial y\partial x}(\theta,\eta)\right)=\left(\frac{\partial^{2}f}{\partial x\partial y}(\overline{\theta},\overline{\eta})\right)$$
Tomando limite cuando $h_{1},h_{2}\rightarrow 0$ y usando la continuidad asumida de las parciales mixtas se tiene que $\theta,\overline{\theta}\rightarrow x$ y $\eta,\overline{\eta}\rightarrow y$ se concluye
$$\frac{\partial^{2}f}{\partial y\partial x}(x,y)=\frac{\partial^{2}f}{\partial x\partial y}(x,y)$$ $\square$

$\textbf{Ejemplo}$

Sea $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=x^{3}+3x^{2}y-2x^{2}y^{2}-y^{4}+3xy$\
En este caso
$$\frac{\partial f}{\partial x}=3x^{2}+6xy-4xy^{2}+3y$$
$$\frac{\partial f}{\partial y}=3x^{2}-4x^{2}y-4y^{3}+3x$$
$$\frac{\partial^{2} f}{\partial x^{2}}=6x+6y-4y^{2}$$
$$\frac{\partial^{2} f}{\partial y^{2}}=-4x^{2}-12y^{2}$$
$$\frac{\partial^{2} f}{\partial x\partial y}=6x-8xy+3$$
$$\frac{\partial^{2} f}{\partial y\partial x}=6x-8xy+3$$
$\textbf{Ejemplo.}$ Dada la función

tenemos que para $(x,y)\neq (0,0)$
$$\frac{\partial f}{\partial x}=y\frac{x^{4}+4x^{2}y^{2}-y^{4}}{(x^{2}+y^{2})^{2}}$$
$$\frac{\partial f}{\partial y}=x\frac{x^{4}-4x^{2}y^{2}-y^{4}}{(x^{2}+y^{2})^{2}}$$
para el primer caso hacemos $x=0$ y tenemos
$$\frac{\partial f}{\partial x}=y\frac{x^{4}+4x^{2}y^{2}-y^{4}}{(x^{2}+y^{2})^{2}}\underbrace{=}{x=0}-y$$ para el segundo caso hacemos $y=0$ y tenemos $$\frac{\partial f}{\partial y}=x\frac{x^{4}-4x^{2}y^{2}-y^{4}}{(x^{2}+y^{2})^{2}}\underbrace{=}{y=0}1$$
Calculamos ahora
$$\frac{\partial^{2} f}{\partial y\partial x}=\frac{\partial^{2} (-y)}{\partial y\partial x}=-1$$
$$\frac{\partial^{2} f}{\partial x\partial y}=\frac{\partial^{2} (1)}{\partial x\partial y}=1$$
por lo tanto
$$\frac{\partial^{2} f}{\partial y\partial x}=-1\neq 1=\frac{\partial^{2} f}{\partial x\partial y}$$
En este caso las parciales segundas no son contiuas en $(0,0)$

$\textbf{Teorema.}$ $\textcolor{Red}{\textbf{Caso General}}$

Sea $f:A\subset\mathbb{R}^{n}\rightarrow\mathbb{R}$ definida en el abierto A de $\mathbb{R}^{n}$ tal que
$$\frac{\partial^{2} f}{\partial x_{i}\partial x_{j}}$$ sean continuas en A, entonces
$$\frac{\partial^{2} f}{\partial x_{i}\partial x_{j}}=\frac{\partial^{2} f}{\partial x_{j}\partial x_{i}}$$

$\textcolor{Red}{\textbf{Caso particular de la regla de la cadena}}$

Supongamos que $C:\mathbb{R}\rightarrow\mathbb{R}^{3}$ es una trayectoria diferenciable y $f:\mathbb{R}^{3}\rightarrow\mathbb{R}$.

Sea $h(t)$=$f(x(t), y(t), z(t))$ donde $c(t)$=$(x(t),y(t), z(t))$.
Entonces

$$\displaystyle\frac{\partial{h}}{\partial{t}} = \displaystyle\frac{\partial{f}}{\partial{x}}\cdot \frac{\partial{x}}{\partial{t}}+\frac{\partial{f}}{\partial{y}}\cdot
\frac{\partial{y}}{\partial{t}}+\frac{\partial{f}}{\partial{z}}\cdot
\frac{\partial{z}}{\partial{t}}$$

Esto es:
$\displaystyle\frac{\partial{h}}{\partial{t}}$=$\nabla{f(c(t))}\cdot
{c'(t)}$, ~donde $c'(t)$=$((x'(t), y'(t), z'(t))$

$\small{Dem.}$ Por definición
$\displaystyle\frac{\partial{h}}{\partial{t}}(t_{0})$=$\displaystyle\lim_{t\rightarrow0}\displaystyle\frac{h(t)-h(t_{0})}{t-t_{0}}$
Sumando y restando tenemos que

$\displaystyle\frac{h(t)-h(t_{0})}{t-t_{0}}$=$\displaystyle\frac{f(c(t))-f(c(t_{0}))}{t-t_{0}}$=$\displaystyle\frac{f(x(t), y(t), z(t)) – f(x(t_{0}), y(t_{0}), z(t_{0}))}{t-t_{0}}$=

=$\frac{f(x(t), y(t), z(t))~-~f(x(t_{0}), y(t),
z(t))~+~f(x(t_{0}), y(t), z(t))~-~f(x(t_{0}), y(t_{0}),
z(t))~+~f(x(t_{0}), y(t_{0}), z(t))~-~f(x(t_{0}), y(t_{0}),
z(t_{0}))}{t-t_{0}}$…$\ast$

Aplicando el Teorema del valor medio $\textbf{(T.V.M.)}$

$f(~x(t),~y(t),~z(t))-f(~x(t_{0}),~y(t),~z(t))=\displaystyle\frac{\partial{f}}{\partial{x}}(~c,~y(t),~z(t))~(x(t)-x(t_{0}))$

$f(~x(t_{0}),~y(t),~z(t))-f(~x(t_{0}),~y(t_{0}),~z(t))=\displaystyle\frac{\partial{f}}{\partial{y}}~(x(t),~ d, ~z(t))~(y(t)-y(t_{0}))$

$f(~x(t_{0}),~y(t_{0}),~z(t))-f(~x(t_{0}),~y(t_{0}),~z(t_{0}))=\displaystyle\frac{\partial{f}}{\partial{z}}(~x(t),~y(t),~e)~(z(t)-z(t_{0}))$

$\therefore$$\ast$=$\displaystyle\frac{\partial{f}}{\partial{x}}(~c,~y(t),~z(t))~\displaystyle\frac{x(t)-x(t_{0})}{t-t_{0}}+\displaystyle\frac{\partial{f}}{\partial{y}}~(~x(t),~d,~z(t))~\displaystyle\frac{y(t)-y(t_{0})}{t-t_{0}}$+

$+\displaystyle\frac{\partial{f}}{\partial{z}}~(~x(t),~y(t),~e))~\displaystyle\frac{z(t)-z(t_{0})}{t-t_{0}}$

Tomando $\displaystyle\lim_{t\rightarrow{t_{0}}}$ y por la continuidad de las parciales

$\displaystyle\frac{\partial{h}}{\partial{t}}$=$\displaystyle\frac{\partial{f}}{\partial{x}}~\frac{\partial{x}}{\partial{t}}+ \displaystyle\frac{\partial{f}}{\partial{y}}~\frac{\partial{y}}{\partial{t}}+\displaystyle\frac{\partial{f}}{\partial{z}}~\frac{\partial{z}}{\partial{t}}$

$\textcolor{Red}{\textbf{Ejemplos: Caso particular de la regla de la cadena}}$

$\textbf{Ejemplo.}$ Verificar la regla de la cadena para $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=x^{2}+3y^{2}$ y $c:\mathbb{R}\rightarrow\mathbb{R}^{2}$ dada por $c(t)=(e^{t},\cos(t))$

$\small{Solución.}$En este caso $\displaystyle{h(t)=f\circ c(t)~\Rightarrow~h'(t)=\frac{\partial h}{\partial t}}$ y aplicando la regla de la cadena se tiene
$$\frac{\partial f}{\partial x}(c(t))\cdot \frac{d x(t)}{dt}=\frac{\partial (x^{2}+3y^{2})}{\partial x}\left|{(e^{t},\cos(t))}\right.\cdot\frac{d (e^{t})}{dt}=2x\left|{(e^{t},\cos(t))}\cdot e^{t}\right.=2e^{t}\cdot e^{t}=2e^{2t}$$

$$\frac{\partial f}{\partial y}(c(t))\cdot \frac{d y(t)}{dt}=\frac{\partial (x^{2}+3y^{2})}{\partial y}\left|{(e^{t},\cos(t))}\right.\cdot\frac{d (\cos(t))}{dt}=6y\left|{(e^{t},\cos(t))}\cdot (-sen(t))\right.=6 cos(t) \cdot (- sen(t))$$
por lo tanto
$$h'(t)=2e^{2t}-6\cos(t)\cdot (sen(t))$$

$\textbf{Ejemplo.}$ Verificar la regla de la cadena para $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=xy$ y $c:\mathbb{R}\rightarrow\mathbb{R}^{2}$ dada por $c(t)=(e^{t},\cos(t))$

$\small{Solución.}$

En este caso $\displaystyle{h(t)=f\circ c(t)~\Rightarrow~h'(t)=\frac{\partial h}{\partial t}}$ y aplicando la regla de la cadena se tiene
$$\frac{\partial f}{\partial x}(c(t))\cdot \frac{d x(t)}{dt}=\frac{\partial (xy)}{\partial x}\left|{(e^{t},\cos(t))}\right.\cdot\frac{d (e^{t})}{dt}=y\left|{(e^{t},\cos(t))}\cdot e^{t}\right.=\cos(t)\cdot e^{t}$$

$$\frac{\partial f}{\partial y}(c(t))\cdot \frac{d y(t)}{dt}=\frac{\partial (xy)}{\partial y}\left|{(e^{t},\cos(t))}\right.\cdot\frac{d (cos(t))}{dt}=x\left|{(e^{t},cos(t))}\cdot (-sen(t))\right.=e^{t}\cdot (-sen(t))$$

por lo tanto
$$h'(t)=\cos(t)e^{t}-e^{t}\cdot sen(t)$$

$\textbf{Ejemplo.}$ Verificar la regla de la cadena para $f:\mathbb{R}^{2}\rightarrow\mathbb{R}$ dada por $f(x,y)=e^{xy}$ y $c:\mathbb{R}\rightarrow\mathbb{R}^{2}$ dada por $c(t)=(3t^{2},t^{3})$

$\small{Solución}$ En este caso $\displaystyle{h(t)=f\circ c(t)~\Rightarrow~h'(t)=\frac{\partial h}{\partial t}}$ y aplicando la regla de la cadena se tiene

$$\frac{\partial f}{\partial x}(c(t))\cdot \frac{d x(t)}{dt}=\frac{\partial (e^{xy})}{\partial x}\left|{(3t^{2},t^{3})}\right.\cdot\frac{d (3t^{2})}{dt}=ye^{xy}\left|{(3t^{2},t^{3})}\cdot 6t\right.=t^{3}e^{3t^{5}}6t=6t^{4}e^{3t^{5}}$$

$$\frac{\partial f}{\partial x}(c(t))\cdot \frac{d x(t)}{dt}=\frac{\partial (e^{xy})}{\partial y}\left|{(3t^{2},t^{3})}\right.\cdot\frac{d (t^{3})}{dt}=xe^{xy}\left|{(3t^{2},t^{3})}\cdot 3t^{2}\right.=3t^{2}e^{3t^{5}}3t^{2}=9t^{4}e^{3t^{5}}$$
por lo tanto
$$h'(t)=6t^{4}e^{3t^{5}}+9t^{4}e^{3t^{5}}=15t^{4}e^{3t^{5}}$$

$\textbf{Teorema 1.}$

El gradiente es normal a las superficies de nivel. Sea $f:\mathbb{R}^{3}\rightarrow\mathbb{R}$ una aplicación $C^{1}$ y sea
$(x_{0},y_{0},z_{0})$ un punto sobre la superficie de nivel $S$ definida por $f(x,y,z)$=$k$, $k$=$cte$. Entonces $\nabla{f}(x_{0},~y_{0},~z_{0})$ es normal a la superficie de nivel en el siguiente sentido: si $v$ es el vector tangente en $t$=$t_{0}$ de
una trayectoria $c(t)$ con $c(t_{0})$=$(x_{0},~y_{0},~z_{0})$ Entonces $\nabla{f}\cdot {v}$=$0$

que se puede escribir como
$$\left(\frac{\partial f}{\partial x}(x(t),y(t)z(t)),\frac{\partial f}{\partial y}(x(t),y(t)z(t)),\frac{\partial f}{\partial z}(x(t),y(t)z(t))\right)\cdot\left(\frac{dx}{dt},\frac{dy}{dt},\frac{dz}{dt}\right)=0$$
en $t=t_{0}$
$$\nabla f(x(0),y(0),z(0))\cdot c'(t_{0})=0$$

$\textcolor{Red}{\textbf{Plano Tangente}}$

Sea $f:A\subset\mathbb{R}^{3}\rightarrow\mathbb{R}$ una función diferenciable definida en A, y sea
$$S={(x,y,z)\in\mathbb{R}^{3}~|~f(x,y,z)=c}$$

una superficie de nivel de f y $\hat{x}{0}=(x{0},y_{0},z_{0})$ un punto de ella. Considere además, una curva
$$\alpha(t)=(x(t),y(t),z(t))$$
y una curva
$$\beta(t)=(x_{1}(t),y_{1}(t),z_{1}(t))$$

que pasen por $\hat{x}{0}$ con $t\in[a,b]$ en ambos casos y tanto $\alpha$ como $\beta$ diferenciables, se tiene entonces $$(f\circ\alpha)'(t)=f'(\alpha(t))\alpha'(t)=\nabla f(\alpha(t))\cdot \alpha'(t)=0$$ $$(f\circ\beta)'(t)=f'(\beta(t))\beta'(t)=\nabla f(\beta(t))\cdot \beta'(t)=0$$ pues el gradiente $\nabla f(\hat{x}{0})$ en ambos casos es ortogonal tanto al vector $\alpha'(t_{0})$ como al vector $\beta'(t_{0})$ en el punto $\hat{x_{0}}=\alpha(t_{0})=\beta(t_{0})$

Si $\nabla f(\hat{x}{0})\neq 0$, entonces las tangentes a las curvas $\alpha, \beta$ sobre S que pasan por $\hat{x}{0}$

están contenidas en un mismo plano; por lo que el plano tangente a
$$S=\left\{(x,y,z)\in\mathbb{R}^{3}~|~f(x,y,z)=c \right\}$$ se define

$\textbf{Definición}$ El plano tangente a S en $\hat{x}{0}$ se define $$P={\hat{x}~|~\nabla f(\hat{x}{0})\cdot (\hat{x}-\hat{x}_{0})=0}$$

$\textbf{Ejemplo.}$ Hallar el plano tangente a la superficie
$$S=\left\{(x,y,z)\in\mathbb{R}^{3}~|~\frac{x^{2}}{4}-\frac{y^{2}}{9}+z^{2}=1 \right\}$$
en el punto $(2,3,1)$

$\small{Solución.}$

En este caso el gradiente es
$$\nabla f(x,y,z)=\left(\frac{x}{2},-\frac{2}{9}y,2z\right)$$
en el punto $(2,3,1)$ es
$$\nabla f(2,3,1)=\left(1,-\frac{2}{3},2\right)$$
Por tanto la ecuación del plano tangente es
$$\left(1,-\frac{2}{3},2\right)\cdot (x-1,y-3,z-1)=0$$
es decir
$$3x-2y+6z-6=0$$