Introducción

calcular la longitud de arco de una curva no solo nos permite medir “cuánto mide” la trayectoria, sino que también nos introduce de manera natural en la idea de cómo cambia la curva punto a punto. Es precisamente en este contexto donde surgen de manera natural los vectores tangente, normal y binormal.

Plano Tangente

Sea $f:[a,b]\rightarrow\mathbb{R}^{n}$ una curva tal que el vector derivada $f'(t)\neq 0$ para todo $t\in[a,b]$, es tangente a f y apunta en la dirección que el parámetro t crece.
Definición. Dada una curva $f:[a,b]\rightarrow\mathbb{R}^{n}$, el vector unitario tangente $T$ es otra función vectorial asociada a la curva, y está definida por:
\[
T(t)=\frac{f^{\prime}(t)}{\|f^{\prime}(t)\|}\ \ \ \ \text{si}\ \ \ \|f^{\prime}(t)\| \neq 0.
\]
Si en la definición anterior, la curva está parametrizada por longitud de arco, considerando que $\|\overline{f}'(s)\|=1$, se tiene que
$$T(s)=\overline{f}'(s)$$

Propiedades del Vector Tangente

(a) En este caso se tiene que
\[
\|T(t)\|= \left\| \frac{f^{\prime}(t)}{\|f^{\prime}(t)\|} \right\|=
\frac{1}{\|f^{\prime}(t)\|} \|f^{\prime}(t)\|=1
\]
por lo tanto $T$ es de magnitud constante.
(b) Tenemos que
\begin{align*} \|T(t)\|=1&\Rightarrow \|T(t)\|^2=1\\&\Rightarrow \frac{d}{dt}\left(\|T(t)\|^2\right)=0\\&\Rightarrow \frac{d}{dt}\left(T(t)\cdot T(t)\right)=0\\&\Rightarrow T'(t)\cdot T(t)+T(t)\cdot T'(t)=0\\&\Rightarrow 2T(t)\cdot T'(t)=0\\&\rightarrow T(t)\cdot T'(t)=0\end{align*}
Esto es $T(t)$ y $T'(t)$ son ortogonales. Este resultado nos permite definir un vector unitario ortogonal a $T(t)$ y que tiene la misma dirección que $T'(t)$.

Vector Normal Principal

Definición. Si $\|T^{\prime}(t)\|\neq 0$ el vector unitario que tiene la misma dirección que $T^{\prime}$ se llama Normal Principal a la curva y se designa por $N(t)$. Asi pues $N(t)$ es una nueva función vectorial asociada a la curva y esta dada por la ecuación:
\[
N(t)=\frac{T^{\prime}(t)}{\|T^{\prime}(t)\|},\ \ \ \ \text{si} \ \ \|T^{\prime}(t)\| \neq 0
\]
Notese que
$$\|N(t)\|=\left\|\frac{T^{\prime}(t)}{\|T^{\prime}(t)\|}\right\|=1$$
Si en la definición anterior, la curva está parametrizada por
longitud de arco, considerando que $T(s)=\overline{f}'(s)$ , se tiene
$$N(s)=\frac{\overline{f}^{\prime\prime}(s)}{|\overline{f}^{\prime\prime}(s)|}=\frac{T'(s)}{\|T'(s)\|}$$

Vector Binormal

Un tercer vector definido mediante
$$B(t)=T(t)\times N(t)$$
recibe el nombre de Vector binormal.
Notese que $$\|B(t)\|=\|T(t)\times
N(t)\|=\|T(t)\|\|N(t)\|\sin\left(\frac{\pi}{2}\right)=1$$
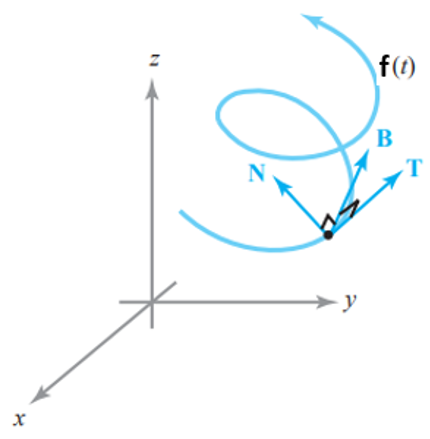
En el punto correspondiente a $f(t)$ en la curva, los vectores $T(t)$, $N(t)$ y $B(t)$ conforman un trío de vectores unitarios y mutuamente ortogonales. Estos dan lugar a un sistema de coordenadas llamado sistema de referencia TNB o sistema de referencia de Frenet-Serret de la curva C.
Los vectores $T(t)$, $N(t)$ y $B(t)$ juegan en el punto de la curva correspondiente a $f(t)$ un papel similar al que juega la tríada i, j y k en el origen del espacio tridimensional. Esta última tríada permace fija, en cambio los vectores $T(t)$, $N(t)$ y $B(t)$ conforman una tríada movil que se mueve a lo largo de la curva.

Ejemplo. Dada la curva $r(t)=\cos t \hat{i}+\sin t \hat{j} + t\hat{k}$ cuya parametrización por longitud de arco es
\[
\bar{r}(s)=\left(\cos\left(\frac{s}{\sqrt{2}}\right),\sin\left(\frac{s}{\sqrt{2}}\right),\frac{s}{\sqrt{2}}\right)
\]
Hallar los vectores Tangente, Normal y Binormal en un punto $r(s)$.
Solución.

Vector Tangente
\[
T(s)=\frac{f^{\prime}(s)}{\|f^{\prime}(s)\|}=
\left(
-\frac{1}{\sqrt{2}} \sin\left(\frac{s}{\sqrt{2}}\right),
\frac{1}{\sqrt{2}}\cos \left(\frac{s}{\sqrt{2}}\right),
\frac{1}{\sqrt{2}}
\right)
\]
Vector Normal
\[
N(s)=\frac{T^{\prime}(s)}{\|T^{\prime}(s)\|}=
\left(
-\frac{1}{\sqrt{2}}\cos\left(\frac{s}{\sqrt{2}}\right)\left(\frac{1}{\sqrt{2}}\right),
-\frac{1}{\sqrt{2}}\left(\frac{1}{\sqrt{2}}\right)\sin\left(\frac{s}{\sqrt{2}}\right),0
\right)
\]
Vector Binormal
\[
B(s)=T(s)\times N(s)=\left|
\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
\frac{-1}{\sqrt{2}}\sin\left(\frac{s}{\sqrt{2}}\right) & \frac{1}{\sqrt{2}}\cos\left(\frac{s}{\sqrt{2}}\right) & \frac{1}{\sqrt{2}}\\
-\cos\left(\frac{s}{\sqrt{2}}\right) & -\sin\left(\frac{s}{\sqrt{2}}\right) & 0\\
\end{array}
\right|=
\left(
\frac{1}{\sqrt{2}}\sin\left(\frac{s}{\sqrt{2}}\right),
\frac{-1}{\sqrt{2}}\cos\left(\frac{s}{\sqrt{2}}\right),
\frac{1}{\sqrt{2}}
\right).~~ \blacksquare
\]

Plano Osculador

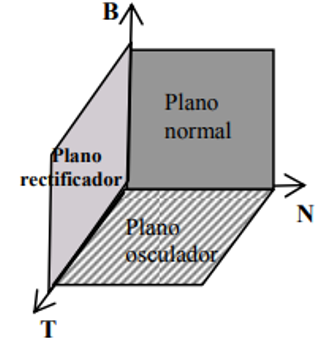
Sea $f:[a,b]\rightarrow\mathbb{R}^{3}$ una curva con triada móvil $T(t)$, $N(t)$ y $B(t)$. Sea $P=(x_{0},y_{0},z_{0})$ un punto de la curva f tal que $f(t_{0})=(x_{0},y_{0},z_{0})$. Se llama Plano Osculador de f en el punto P, al plano que pasa por P y es paralelo a los vectores $T(t_{0})$ y $N(t_{0})$. Este plano tiene por ecuación
$$\boxed{B(t_{0})\cdot [(x,y,z)-(x_{0},y_{0},z_{0})]=0}$$ El plano osculador es el plano que mejor se adapta a la curva en cada uno de sus puntos. Si la curva es plana, el plano osculador coincide con el plano de la curva.
Ejemplo. Consideremos la curva $f:\mathbb{R}\rightarrow\mathbb{R}^3$ dado por:
\[ f(s)=\left(
\cos\left(\frac{s}{\sqrt{2}}\right),
\sin\left(\frac{s}{\sqrt{2}}\right),
\frac{s}{\sqrt{2}}
\right)
\]
el cual es dos veces diferenciable parametrizado por longitud de arco y que describe una hélice circular en $\mathbb{R}^3$. Obtenga la ecuación del plano osculador en el punto $f(\sqrt{2}\pi)=(-1,0,\pi)$.
Solución.
Tenemos que:
\[ T(s)=\frac{f^{\prime}(s)}{\|f^{\prime}(s)\|}= \left( -\frac{1}{\sqrt{2}} \sin\left(\frac{s}{\sqrt{2}}\right), \frac{1}{\sqrt{2}}\cos \left(\frac{s}{\sqrt{2}}\right), \frac{1}{\sqrt{2}} \right) \]
y $T(\sqrt{2}\pi)=\left(0,-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}\right)$, por otro lado:
\begin{align*}N(s)&=\frac{T^{\prime}(s)}{\|T^{\prime}(s)\|}\\&=\left(
-\frac{1}{\sqrt{2}}\cos\left(\frac{s}{\sqrt{2}}\right)\left(\frac{1}{\sqrt{2}}\right),
-\frac{1}{\sqrt{2}}\left(\frac{1}{\sqrt{2}}\right)\sin\left(\frac{s}{\sqrt{2}}\right),0
\right)\\&=\left(
-\left(\frac{1}{2}\right)\cos\left(\frac{s}{\sqrt{2}},\right),-\left(\frac{1}{2}\right)\sin\left(\frac{s}{\sqrt{2}}\right),0
\right)\end{align*}
y $N(\sqrt{2}\pi)=(1,0,0)$.
Por lo que
\[ T(\sqrt{2}\pi)\times N(\sqrt{2}\ \pi) =\left| \begin{array}{ccc} \hat{i} & \hat{j} & \hat{k} \\ \frac{-1}{\sqrt{2}}\sin\left(\frac{s}{\sqrt{2}}\right) & \frac{1}{\sqrt{2}}\cos\left(\frac{s}{\sqrt{2}}\right) & \frac{1}{\sqrt{2}}\\-\left(\frac{1}{2}\right)\cos\left(\frac{s}{\sqrt{2}}\right) & -\left(\frac{1}{2}\right)\sin\left(\frac{s}{\sqrt{2}}\right) & 0\\ \end{array}\right|= \left(\frac{1}{2\sqrt{2}}\sin\left(\frac{s}{\sqrt{2}}\right),\frac{-1}{2\sqrt{2}}\cos\left(\frac{s}{\sqrt{2}}\right),\frac{1}{2\sqrt{2}} \right) \]
al evaluar en $\sqrt{2}\ \pi$ nos queda $\displaystyle{\left(0,\frac{1}{2\sqrt{2}},\frac{1}{2\sqrt{2}}\right)}$. Por lo tanto la ecuación del plano osculador en $P=(-1,0,\pi)$ es: \[ (x+1,y,z-\pi)\cdot\left(0,\frac{1}{2\sqrt{2}},\frac{1}{2\sqrt{2}}\right)=0 \] \[ \Rightarrow \frac{1}{2\sqrt{2}} (y) +\frac{1}{2\sqrt{2}} (z-\pi)=0 \] \[ \Rightarrow y+z=\pi.~~ \blacksquare \]

Plano Normal

Se llama Plano Normal de f en el punto P, al plano que pasa por P y es paralelo a los vectores $N(t_{0})$ y $B(t_{0})$. Este plano tiene por ecuación
$$\boxed{T(t_{0})\cdot [(x,y,z)-(x_{0},y_{0},z_{0})]=0}$$
Ejemplo. Consideremos la curva $f:\mathbb{R}\rightarrow
\mathbb{R}^3$ dado por:
\[ f(t)=\left( 2\cos\left(t\right), 2\sin\left(t\right), t \right) \] el cual es dos veces diferenciable y que describe una hélice circular en $\mathbb{R}^3$. Obtenga la ecuación del plano normal en el punto $f\left(\frac{\pi}{2}\right)=\left(0,2,\frac{\pi}{2}\right)$.
Solución. Tenemos que:
\[ T(t)=\frac{1}{\sqrt{5}}\left(-2\sin(t),2\cos(t),1\right) \] y $\displaystyle{T\left(\frac{\pi}{2}\right)=\frac{1}{\sqrt{5}}\left(-2,0,1\right)}$. Por lo tanto la ecuación del plano normal es: \[ \frac{1}{\sqrt{5}}(-2,0,1)\cdot\left[(x,y,z)-\left(0,2,\frac{\pi}{2}\right)\right]=0 \] \[ \Rightarrow 4x-2z+\pi=0.~~\blacksquare \]

Plano Rectificador

Se llama Plano rectificador de f en el punto P, al plano que pasa por P y es paralelo a los vectores $T(t_{0})$ y $B(t_{0})$. Este plano tiene por ecuación
$$\boxed{N(t_{0})\cdot [(x,y,z)-(x_{0},y_{0},z_{0})]=0}$$
Ejemplo. Consideremos la curva $f:\mathbb{R}\rightarrow \mathbb{R}^3$ dada por:
\[ f(t)=\left( 2\cos\left(t\right), 2\sin\left(t\right), t \right) \] la cual es dos veces diferenciable y que describe una hélice circular en $\mathbb{R}^3$. Obtenga la ecuación del plano rectificador en el punto $\displaystyle{f\left(\frac{\pi}{2}\right)=\left(0,2,\frac{\pi}{2}\right)}$.
Solución. Tenemos que: \[ N(t)=\left(-\cos(t),-\sin(t),0\right) \] y $\displaystyle{N\left(\frac{\pi}{2}\right)=\left(0,-1,0\right)}$. Por lo tanto la ecuación del plano rectificador es: \[ (0,-1,0)\cdot\left[(x,y,z)-\left(0,2,\frac{\pi}{2}\right)\right]=0 \] \[ \Rightarrow y-2=0.~~\blacksquare \]

Mas adelante

En la siguiente entrada veremos como a partir de vectores caracterizados en esta entrada podemos definir y calcular la curvatura y radio de curvatura de una curva o plano.

Tarea Moral

1.- Determina $T$ y $N$ para cada una de las siguientes curvas:

La parábola $x=pt^2$ , $y=2pt$.

La elipse $f(\theta)=(acos\theta, b sen\theta)$, $\theta \in [0,2\pi]$; $a,b>0$

2.- Si una curva está descrita por $f(t)= (t,t^2,t^3)$, determína $T(t)$, $N(t)$, $B(t)$ y el plano osculador cuando $t=0$ y $t=1$

3.- Si $C$ es una curva en $R^3$ descrita por $f$ demuestra que

$B=\dfrac{f’ \times f^{‘ ‘}}{|f’ \times f^{‘ ‘} |}$, $N=B \times T= \dfrac{(f’ \times f^{‘ ‘})\times f’}{| (f’ \times f^{‘ ‘} \times f’)|}$

4.- Demuestra que si una curva $C$ se encuentra en el plano $P$ en $R^3$ entonces el plano osculador en cualquier punto de $C$ es $P$.

5.- Determina $T,N$ y $B$ y el plano osculador en $f(0)$ para las curvas en seguida descritas.

a) $f(t)= (t cost, t sent, t)$

b) $f(t)= (t-sent, 1-cost, t)$

Enlaces

El siguiente interactivo contiene un visualizador de las funciones vectoriales parábola y circunferencia con su vector tangente. Si tienes experiencia con el código puedes implementar cualquier otra función de tu elección.

https://colab.research.google.com/drive/1LIc0KHRJnTz9e-CLPEb9d4KZyr2Vdytq?usp=sharing