Introducción

En el año de 1685 el matemático británico John Wallis planteó en su libro «De algebra tractatus» la primera idea sobre la existencia de una correspondencia entre los puntos del plano y los números complejos, aunque ésta no tuvo gran influencia entre sus contemporáneos pues era un tanto confusa. Es hasta el año de 1798 cuando el topógrafo noruego Caspar Wessel da una propuesta seria, en su libro «On the Analytical Representation of Direction«, de una primera representación de los números complejos a través de puntos en un plano. Aunque el trabajo de Wessel permaneció oculto hasta su traducción al francés en 1897, la idea de Wessel era tratar a los números complejos como segmentos de líneas dirigidos, por lo que introduce un eje imaginario, perpendicular al eje de los números reales, asigna la letra griega $\varepsilon$ para denotar a la unidad imaginaria $\sqrt{-1}$ e identifica entonces a los números complejos como puntos en el plano, es decir intuitivamente los tratan como vectores en 2 dimensiones, por lo que las operaciones con las que los trata coinciden con las operaciones de vectores usuales, obteniendo así una primera representación geométrica de estos números.

Otra interpretación geométrica de los números complejos fue dada por el contador suizo Jean Robert Argand, quien en su libro «Essai sur une manière de représenter les quantités imaginaires dans les constructions géometriques«, interpreta a $\sqrt{-1}$ como una rotación de un ángulo recto en el plano. Su justificación se basaba en el hecho de que $\sqrt{-1} \sqrt{-1} = -1$, es decir dos rotaciones de un ángulo recto son equivalentes a una rotación de dos ángulos rectos. El trabajo de Argand es quizás de los más trascendentes pues la forma en que representa a los números en el plano, denominado como el plano de Argand, es básicamente la que usamos hoy en día.

Para 1749, Leonhard Euler redacta en su escrito «De la controverse entre Mrs. Leibnitz et Bernoulli sur les logarithmes des nombres négatifs et imaginaires«, que para localizar un número imaginario $x$ en el plano solo basta con tomar un arco $g$ de la circunferencia de radio $r$ y determinar su seno y coseno, entonces dicho número está determinado por:

\begin{equation*}
x = r \left(\text{cos}(g) + \sqrt{-1} \, \text{sen}(g)\right).
\end{equation*}

Es gracias al trabajo de Carl Friedrich Gauss que se logra por fin unificar todas estas ideas y poder dar sin duda una relación de los números complejos y el plano complejo. Alrededor del año de 1796, Gauss estaba de acuerdo con la asociación de los números complejos con puntos en el plano, tanto que para el año de 1799 hizo uso de esa idea en su trabajo para probar el Teorema Fundamental del Álgebra. En 1811 Gauss redactó en uno de sus escritos con Bessel que «tal como uno puede pensar en todo el dominio de las magnitudes reales representado como una línea recta, así también el dominio completo de todas las magnitudes, tanto números reales como números imaginarios, puede ser visualizado como un plano infinito, en el cual el punto definido por la ordenada $a$ y la abscisa $b$, igualmente representa a la magnitud $a+ib$».

Es hasta 1835 que el matemático británico William Rowan Hamilton en su trabajo «Theory of Conjugate Functions, or Algebra Couples, with a Preliminary and Elementary Essay on Algebra as the Science of Pure Time«, da la primera definición de un número complejo como un par ordenado de números reales, tal y como la conocemos hoy en día.

Si deseas conocer más acerca de la historia de los números complejos puedes consultar los libros An Introduction to Complex Analysis de Agarwal, Ravi P., y Numbers de Ebbinghaus, H.D.

• https://www.springer.com/gp/book/9780387974972.
• https://www.springer.com/gp/book/9781461401940.

Interpretación geométrica de los números complejos.

Hasta ahora tenemos construido ya el campo de los números complejos, el cual lo definimos como el conjunto:
\begin{equation*}
\mathbb{C} = \{ z = (a,b) \, \, | \, \, a, b \in \mathbb{R}, \, i=(0,1)\}.
\end{equation*}

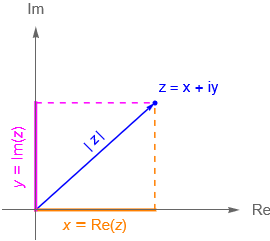
Esta definición de número complejo como un par ordenado es la representación geométrica de un número complejo con la que trabajaremos. Es decir, a cada número complejo de la forma $z=a+ib$, donde $a,b \in \mathbb{R}$, le corresponde el punto $(a, b) = \left(\text{Re}(z), \, \text{Im}(z)\right)$ en el plano cartesiano, de ahora en adelante llamado el plano complejo o el plano de Argand.

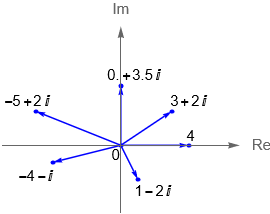
De acuerdo con esta idea, los números reales $a$ son asociados en el plano complejo con puntos en el eje $x$, llamado propiamente como el eje real, mientras que los números complejos puros, es decir de la forma $ib$, corresponden a puntos en el eje $y$ el cual se denomina como el eje imaginario, figura 1.

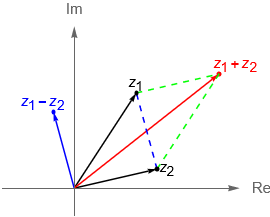
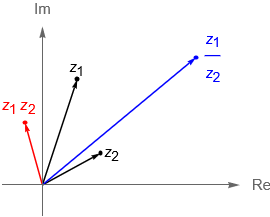
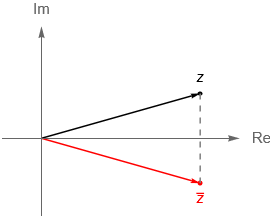
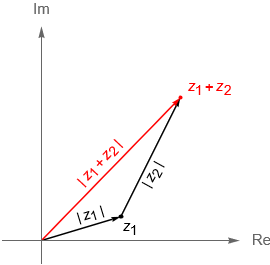
Las operaciones definidas en la entrada previa cobran entonces un sentido geométrico. Mientras que la suma de dos números complejos coincide con la suma vectorial en $\mathbb{R}^2$, figura 2(a), el producto de dos números complejos corresponde a una rotación, seguida de una homotecia en $\mathbb{R}^2$, figura 2(b). Por otra parte, tenemos que el conjugado de un número complejo $z$ resulta ser la reflexión de dicho número a través del eje real, figura 3.

De acuerdo con la figura 4, notemos que la parte real, Re$(z)$, de un número complejo $z$, es la proyección de $z$ sobre el eje real, mientras que su parte imaginaria, Im$(z)$, es la proyección de $z$ sobre el eje imaginario.

Observación 3.1.
Considerando la definición del módulo de un número complejo es fácil verificar que:
\begin{equation*}
\text{máx}\left\{|\,\operatorname{Re}(z)\,|, |\,\operatorname{Im}(z)\,|\right\} \leq |\,z\,| \leq |\,\operatorname{Re}(z)\,| + |\,\operatorname{Im}(z)\,|.
\end{equation*}

Observación 3.2
A diferencia de $\mathbb{R}$, en $\mathbb{C}$ no es posible introducir una propiedad de ser positivo que sea compatible con las operaciones de suma y producto definidas en $\mathbb{C}$, lo cual nos imposibilita el ordenar a los números complejos bajo la relación “$>0$”. Para probar esto, basta ver que dicha propiedad no es compatible con las operaciones de campo, es decir notemos que no se cumplen las siguientes propiedades de manera simultánea:

1. Para todo $z \in \mathbb{C}$, se cumple una y solo una de las siguientes tres condiciones: $z>0$, $z=0$ ó $-z>0$.
2. Si $z>0$ y $w>0$, entonces $z+w>0$ y $zw>0$.

Sin perder generalidad, notemos que si suponemos que $z \neq 0$, entonces se cumple que $z^2>0$. De manera particular tenemos que $1^2>0$, $i^2>0$, por lo que $1^2 + i^2 >0$, pero $1^2 + i^2 = 1 + (-1) = 0$, es decir que $0>0$, lo cual claramente es una contradicción a la antisimetría, por lo que, bajo esta relación de orden, $\mathbb{C}$ no puede ser ordenado.

La observación 3.2 nos deja ver que dados $z_1, z_2 \in \mathbb{C}$ la desigualdad $z_1 < z_2$ no tiene sentido desde que no podemos decir que alguno es mayor que cero. Sin embargo mediante el módulo de un número complejo sí es posible pensar en la desigualdad $| \, z_1 \, | < | \, z_2 \,|$, que de acuerdo con la definición 3.1 nos diría que el punto $z_1$ está más cerca del origen que el punto $z_2$.

Ejemplo 3.1.
Sean $z_1 = -4 + 2i$, $z_2 = 3 – i$ y $z_3 = -4$ entonces:

Como $|\,z_1\,|>|\,z_2\,|$, entonces $z_1$ está más lejos del origen que $z_2$.

Por otra parte, tenemos que $|\,z_3\,|$ simplemente nos determina el valor absoluto del número real $z_3$.

Observación 3.3.
De acuerdo con las observaciones 2.3 y 2.4 sabemos que para $z = a+ib \in \mathbb{C}$ se cumple que $z\overline{z} = a^2 + b^2$, por lo que:
\begin{equation*}
| \, z \, |^2 = z \overline{z}.
\end{equation*}

Si consideramos que $z \neq 0$, tenemos que:
\begin{equation*}
\frac{z \overline{z}}{| \, z \, |^2} = z \, \frac{\overline{z}}{| \, z \, |^2} = 1.
\end{equation*}

Lo anterior nos dice que para $z \neq 0$, podemos calcular el inverso multiplicativo de $z$ como:
\begin{equation*}
z^{-1} = \frac{1}{z} = \frac{\overline{z}}{| \, z \, |^2}.
\end{equation*}
Geométricamente esto nos dice que el inverso de un número complejo $z\neq0$ estará en la dirección de su conjugado $\overline{z}$, pero su módulo estará determinado por el inverso del módulo de $z$, lo cual cobrará mayor sentido en la entrada 6.

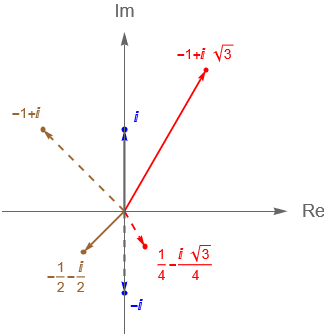
Ejemplo 3.2.
Consideremos los siguientes números complejos:

Entonces:

Proposición 3.1.
Sean $z, w \in \mathbb{C}$, entonces se satisfacen las siguientes igualdades:

1. $|\, z + w \, |^2 = |\, z \, |^2 + 2 \, \text{Re}(z \overline{w}) + |\, w \, |^2$.
2. Ley de cosenos.
   \begin{equation*}
   |\, z – w \, |^2 = |\, z \, |^2 – 2 \, \text{Re}(z \overline{w}) + |\, w \, |^2.
   \end{equation*}
3. Identidad del paralelogramo.
   \begin{equation*}
   |\, z + w \, |^2 + |\, z – w \, |^2 = 2 \left(|\, z \, |^2 + |\, w \, |^2\right).
   \end{equation*}
4. $| \, z w \,| = |\,z\,| \, |\,w\,|$.
5. $\text{Re}(z \pm w) = \text{Re}(z) \pm \text{Re}(w)$ y $\text{Im}(z \pm w) = \text{Im}(z) \pm \text{Im}(w)$.
6. Para $\alpha \in \mathbb{R}$, $\alpha\,\text{Re}(z) = \text{Re}(\alpha z)$ y $\alpha\,\text{Im}(z) = \text{Im}(\alpha z)$.
7. Si $w \neq 0$, entonces $\left| \dfrac{z}{w} \right| = \dfrac{|\,z\,|}{|\,w|\,}$.
8. $|\, z \,| = |\, \overline{z} \,|$.

Demostración. Dadas las hipótesis y considerando las observaciones 2.3 y 2.4, tenemos que:

1. 
   \begin{align*}
   |\, z + w \, |^2 & = \left( z + w \right)\overline{\left( z + w \right)}\\
   & = \left( z + w \right) \left( \overline{z} + \overline{w} \right)\\
   & = z \overline{z} + z \overline{w} + \overline{z}w + w \overline{w}\\
   & = |\, z \, |^2 + z \overline{w} + \overline{z \overline{w}} + |\, w \, |^2\\
   & = |\, z \, |^2 + 2 \, \text{Re}(z \overline{w}) + |\, w \, |^2.
   \end{align*}
2. Se deja como ejercicio al lector.
3. Considerando 1 y 2 tenemos que:
   \begin{align*}
   |\, z + w \, |^2 + |\, z – w \, |^2 & = \left(|\, z \, |^2 + 2\,\text{Re}(z \overline{w}) + |\, w \, |^2\right) + \left(|\, z \, |^2 – 2 \, \text{Re}(z \overline{w}) + |\, w \, |^2\right)\\
   & = 2 \, |\, z \, |^2 + 2 \, |\, w \, |^2\\
   & = 2 \left(|\, z \, |^2 + |\, w \, |^2\right)
   \end{align*}
4. Sabemos que para todo $z\in\mathbb{C}$ se tiene que $|\,z\,|\geq0$, por lo que:
   \begin{equation*}
   |\,zw\,|^2 = \left(zw\right)\left(\overline{zw}\right) = \left(z \overline{z} \right)\left(w \overline{w}\right) = |\,z\,|^2 |\,w\,|^2.
   \end{equation*}

Entonces $|\,zw\,| = |\,z\,|\, |\,w\,|$.

5. Se deja como ejercicio al lector.
6. Se deja como ejercicio al lector.
7. Supongamos que $w\neq0$, entonces $|\,w\,|>0$, por lo que considerando el punto 4 tenemos que:
   \begin{equation*}
   |\, z \,| = \left|\,\frac{z}{w}\, w\,\right| = \left|\,\frac{z}{w}\,\right|\,|\, w\,|, \quad \Longrightarrow \quad \frac{|\,z\,|}{|\,w\,|} = \left|\,\frac{z}{w}\,\right|.
   \end{equation*}
8. Se deja como ejercicio al lector.

$\blacksquare$

Observación 3.4.
Las propiedades 4, 5 y 6 de esta proposición se pueden generalizar por medio de inducción matemática, es decir para $z_1, z_2, \ldots, z_n \in\mathbb{C}$, con $n\geq2$, se cumple que:

\begin{equation*}
|\,z_1 z_2 \cdots z_n\,| = |\,z_1\,| \, |\,z_2\,| \cdots |\,z_n\,|.
\end{equation*}

\begin{equation*}
\operatorname{Re}(z_1 + z_2 + \cdots + z_n) =\operatorname{Re}(z_1) + \operatorname{Re}(z_2) + \cdots + \text{Re}(z_n).
\end{equation*}

\begin{equation*}
\operatorname{Im}(z_1 + z_2 + \cdots + z_n) = \operatorname{Im}(z_1) + \operatorname{Im}(z_2) + \cdots + \operatorname{Im}(z_n).
\end{equation*}

Es importante notar que al igual que el valor absoluto satisface la desigualdad del triángulo en $\mathbb{R}$, el módulo en $\mathbb{C}$ también la cumple.

Proposición 3.2. (Desigualdad del triángulo.)
Para todo $z_1,z_2\in\mathbb{C}$ se cumple que:

\begin{equation*}
|\,z_1 + z_2\,| \leq |\,z_1\,| + |\,z_2\,|
\end{equation*}

Demostración. De acuerdo con la observación 3.1 tenemos que para todo $z \in \mathbb{C}$ se cumple:
\begin{equation*}
\operatorname{Re}(z) \leq \left|\,\operatorname{Re}(z)\,\right| \leq \left|\,z\,\right|. \tag{3.1}
\end{equation*}

Considerando la proposición 3.1, incisos 4 y 6, tenemos que:
\begin{equation*}
|\, z_1 \,| \, |\, z_2 \,| = |\, z_1 \,| \, |\, \overline{z_2} \,| = |\, z_1 \overline{z_2}\,|.
\end{equation*}

Entonces, por (3.1) se sigue que:
\begin{equation*}
\operatorname{Re}(z_1\overline{z_2}) \leq |\, z_1 \overline{z_2}\,|.
\end{equation*}

Por otra parte, por la proposición 3.1 inciso 1, se tiene que:
\begin{align*}
|\, z_1 + z_2 \, |^2 & = |\, z_1 \, |^2 + 2 \, \operatorname{Re}(z_1 \overline{z_2}) + |\, z_2 \, |^2 \\
& \leq |\, z_1 \, |^2 + 2 \, |\, z_1 \overline{z_2}\,| + |\, z_2 \, |^2\\
& = |\, z_1 \, |^2 + 2\,|\, z_1 \,| \, |\,\overline{z_2}\,| + |\, z_2 \, |^2\\
& = |\, z_1 \, |^2 + 2\,|\, z_1 \,| \, |\,z_2\,| + |\, z_2 \, |^2\\
& = \left( | \, z_1 \, | + | \, z_2 \, | \right)^2.
\end{align*}

Como $| \, z \,| \geq 0 $ para todo $z \in \mathbb{C}$, entonces tomando raíz cuadrada en la desigualdad se sigue que:
\begin{equation*}
| \, z_1 + z_2 \, | \leq | \, z_1 \, | + | \, z_2 \,|.
\end{equation*}

$\blacksquare$

De manera geométrica podemos comprobar que se satisface la desigualdad del triángulo:

Observación 3.5.
Consideremos la proposición 3.2, tenemos que:
\begin{equation*}
\operatorname{Re} \left(z_1\,\overline{z_2}\right) = |\,z_1\,\overline{z_2}\,| \quad \Longleftrightarrow \quad z_1\,\overline{z_2} \in \mathbb{R} \,\, \text{y} \, \, z_1\,\overline{z_2}\geq 0.
\end{equation*}

La cual es una condición necesaria y suficiente para que se cumpla la igualdad en la desigualdad del triángulo. (¿Por qué?)

Notemos que si $z_2 \neq 0$, entonces $z_1\,\overline{z_2} = \dfrac{z_1 |z_2|^2}{z_2}$, por lo que (¿Por qué?):
\begin{equation*}
z_1\,\overline{z_2} \in \mathbb{R} \,\, \text{y} \, \, z_1\,\overline{z_2}\geq0 \quad \Longleftrightarrow \quad \frac{z_1}{z_2}\geq0.
\end{equation*}

Entonces:
\begin{align*}
|\, z_1 + z_2 \,| &= \left|\,\left(\frac{z_1}{z_2} + 1 \right)z_2\,\right|\\
&= \left|\,\frac{z_1}{z_2} + 1 \,\right|\,|\,z_2\,|\\
&= \left(\frac{|\,z_1\,|}{|\,z_2\,|} + 1 \right) |\,z_2\,|\\
&=|\,z_1\,| + |\,z_2\,|.
\end{align*}

Una consecuencia de la desigualdad del triángulo es:

Proposición 3.3.
Para todo $z_1, z_2 \in \mathbb{C}$ se cumple que:
\begin{equation*}
\left| \, | \, z_1 \, | – | \, z_2 \,| \, \right| \leq | \, z_1 \pm z_2 \, |.
\end{equation*}

Demostración.
Se deja como ejercicio al lector.

$\blacksquare$

Ejemplo 3.3.
Sea $z$ un número complejo tal que $|\, z \,| = 1$, entonces:
\begin{equation*}
1 = |\, – 1 \,| = |\, 1 – 2 \,| = |\, |\,z\,| – 2 \,| \leq |\, z – 2\,|.
\end{equation*}

\begin{equation*}
|\, z – 2\,| \leq |\,z\,| + 2 = 1 + 2 = 3.
\end{equation*}

Observación 3.6.
La desigualdad del triángulo se puede generalizar mediante inducción matemática para un número finito de términos, es decir:
\begin{equation*}
|\, z_1 + z_2 + \cdots + z_n\,| \leq |\,z_1\,| + |\,z_2\,| + \cdots + |\,z_n\,|, \quad \forall n \geq 2.
\end{equation*}

o simplemente:
\begin{equation*}
\left|\, \sum_{i=1}^n z_i \,\right| \leq \sum_{i=1}^n |\,z_i\,|, \quad \forall n \geq 2.
\end{equation*}

Otro resultado importante es la siguiente desigualdad:

Proposición 3.4. (Desigualdad de Cauchy – Schwarz para números complejos.)
Si $z_1, \ldots, z_n$ y $w_1, \ldots, w_n$ son números complejos, entonces:
\begin{equation*}
\left|\, \sum_{i=1}^n z_i w_i \,\right|^2 \leq \sum_{i=1}^n \left|\,z_i\,\right|^2 \sum_{i=1}^n \left|\,w_i\,\right|^2, \quad \forall n \geq 2.
\end{equation*}

Demostración. Dadas las hipótesis, tenemos sin pérdida de generalidad que:
\begin{equation*}
\sum_{i=1}^n \left|\,w_i\,\right|^2 = 0 \quad \Longleftrightarrow \quad \left|\,w_i\,\right|^2 = 0, \quad \forall i \in {1, \ldots, n} \quad \Longleftrightarrow \quad w_i = 0, \quad \forall i \in {1, \ldots, n}.
\end{equation*}

Por lo que en caso de que $w_i = 0, \, \forall i \in {1, \ldots, n}$, es claro que se cumple la igualdad. Entonces, sin pérdida de generalidad supongamos que $\sum_{i=1}^n \left|\,w_i\,\right|^2 \neq 0$.

Notemos que para cualquier $\lambda \in \mathbb{C}$ se cumple que:
\begin{equation*}
0 \leq \sum_{i=1}^n \left|\,z_i – \lambda \overline{w_i}\,\right|^2.
\end{equation*}
De acuerdo con la proposición 3.1 tenemos que:
\begin{align*}
\sum_{i=1}^n \left|\,z_i – \lambda \overline{w_i}\,\right|^2 & = \sum_{i=1}^n \left( \left|\,z_i\,\right|^2 + \left|\,w_i\,\right|^2 – 2 \, \text{Re}\left(z_i \overline{\lambda \overline{w_i}}\right) \right)\\
& = \sum_{i=1}^n \left|\,z_i\,\right|^2 + \left|\,\lambda\,\right|^2\sum_{i=1}^n \left|\,w_i\,\right|^2 – 2 \, \sum_{i=1}^n \text{Re}\left(z_i \overline{\lambda} w_i\right)\\
& = \sum_{i=1}^n \left|\,z_i\,\right|^2 + \left|\,\lambda\,\right|^2\sum_{i=1}^n \left|\,w_i\,\right|^2 – 2\,\text{Re}\left( \overline{\lambda} \sum_{i=1}^n z_i w_i\right). \tag{3.2}
\end{align*}

Por otra parte, dado que $\lambda$ es arbitrario y $\sum_{i=1}^n \left|\,w_i\,\right|^2 \neq 0$, entonces podemos tomarlo de la forma:
\begin{equation*}
\lambda = \frac{\sum_{i=1}^n z_i w_i}{\sum_{i=1}^n \left|\, w_i\,\right|^2} \quad \Longrightarrow \quad \overline{\lambda} = \frac{\overline{\sum_{i=1}^n z_i w_i}}{\sum_{i=1}^n \left|\, w_i\,\right|^2}.
\end{equation*}

Notemos que:
\begin{align*}
\overline{\lambda}\sum_{i=1}^n z_i w_i & = \left( \frac{\overline{\sum_{i=1}^n z_i w_i}}{\sum_{i=1}^n \left|\, w_i\,\right|^2} \right) \left( \sum_{i=1}^n z_i w_i \right)\\
& = \frac{\left|\sum_{i=1}^n z_i w_i\right|^2}{\sum_{i=1}^n \left|\, w_i\,\right|^2} \in \mathbb{R},
\end{align*}

por lo que:
\begin{align*}
– 2\,\text{Re}\left( \overline{\lambda} \cdot \sum_{i=1}^n z_i w_i\right) & = – 2\,\text{Re}\left( \frac{\left|\sum_{i=1}^n z_i w_i\right|^2}{\sum_{i=1}^n \left|\, w_i\,\right|^2}\right)\\
& = – 2 \, \frac{\left|\sum_{i=1}^n z_i w_i\right|^2}{\sum_{i=1}^n \left|\, w_i\,\right|^2}.
\end{align*}

Sustituyendo en (3.2) tenemos que:
\begin{align*}
0 & \leq \sum_{i=1}^n \left|\,z_i\,\right|^2 + \left|\,\frac{\sum_{i=1}^n z_i w_i}{\sum_{i=1}^n \left|\, w_i\,\right|^2} \,\right|^2\sum_{i=1}^n \left|\,w_i\,\right|^2 – 2\,\text{Re}\left( \overline{\lambda} \sum_{i=1}^n z_i w_i\right)\\
& = \sum_{i=1}^n \left|\,z_i\,\right|^2 + \frac{\left|\,\sum_{i=1}^n z_i w_i\,\right|^2}{\sum_{i=1}^n \left|\, w_i\,\right|^2} – 2\,\frac{\left|\,\sum_{i=1}^n z_i w_i\,\right|^2}{\sum_{i=1}^n \left|\, w_i\,\right|^2}.
\end{align*}

Por lo tanto:
\begin{equation*} \frac{\left|\,\sum_{i=1}^n z_i w_i\,\right|^2}{\sum_{i=1}^n \left|\, w_i\,\right|^2} \leq \sum_{i=1}^n \left|\,z_i\,\right|^2 \quad \Longrightarrow \quad \left|\,\sum_{i=1}^n z_i w_i\,\right|^2 \leq \sum_{i=1}^n \left|\,z_i\,\right|^2 \sum_{i=1}^n \left|\, w_i\,\right|^2.
\end{equation*}

$\blacksquare$

Esta desigualdad será de mucha utilidad en la última unidad como criterio para probar la convergencia de algunas series.

Observación 3.7.
La definición de producto interior en un espacio vectorial tiene cierta sutileza cuando se trata de un espacio vectorial complejo, ya que en dado caso es posible hablar de un producto interior hermitiano, es decir la propiedad de simetría que conocemos queda sujeta a la operación de la conjugación compleja, por lo que en algunos textos es común establecer la desigualdad de Cauchy-Schwarz como:
\begin{equation*}
\left|\, \sum_{i=1}^n z_i \overline{w_i} \,\right|^2 \leq \sum_{i=1}^n \left|\,z_i\,\right|^2 \sum_{i=1}^n \left|\,w_i\,\right|^2, \quad \forall n \geq 2, \end{equation*}

ya que $\sum_{i=1}^n z_i \overline{w_i}$ define justamente un producto interior en $\mathbb{C}^n$.

De acuerdo con lo anterior, se puede plantear la siguiente proposición, cuya demostración se obtuvo del libro Principios de Análisis Matemático de Walter Rudin.

Proposición 3.4.1. (Desigualdad de C-S.)
Si $z_1,\ldots,z_n, w_1, \ldots, w_n\in\mathbb{C}$, entonces:
\begin{equation*}
\left|\, \sum_{i=1}^n z_i \overline{w_i} \,\right|^2 \leq \sum_{i=1}^n \left|\,z_i\,\right|^2 \sum_{i=1}^n \left|\,w_i\,\right|^2, \quad \forall n \geq 2. \end{equation*}

Demostración. Dadas las hipótesis, sean $A = \sum_{i=1}^n \left|\,z_i\,\right|^2$, $B = \sum_{i=1}^n \left|\,w_i\,\right|^2$ y $C = \sum_{i=1}^n z_i \overline{w_i}$, entonces:
\begin{align*}
\sum_{i=1}^n |\,Bz_i – Cw_i\,|^2 & = B^2 A – 2\,\text{Re}(B\overline{C}C) + |\,C\,|^2B\\
& = B\left(AB – |C|^2\right)\geq 0.
\end{align*}

Entonces de $|\,C\,|^2 \leq AB$ se sigue el resultado.

$\blacksquare$

Tarea moral

1. Verifica las desigualdades de la observación 3.1.
2. Realiza las demostraciones faltantes en la proposición 3.1.
3. Considera la observación 3.5. Justifica porqué la primera condición es necesaria y suficiente para que se cumpla la igualdad en la proposición 3.2. Explica porqué son equivalentes las últimas dos condiciones.
4. Escribe la demostración de la proposición 3.3 de manera detallada.
5. Realiza por inducción la prueba de la observación 3.6. ¿Qué condición es necesaria y suficiente para que se de la igualdad?
6. Considera la proposición 3.5, ¿es posible probar la desigualdad de Cauchy-Schawrz por inducción?
7. Justifica y desarrolla los pasos de la demostración de la desigualdad de Cauchy-Schwarz dada en la proposición 3.4.1. Argumenta de manera detallada porqué se cumple el resultado.
8. Sean $z_1,z_2,z_3\in\mathbb{C}$. Prueba la siguiente igualdad:
   \begin{equation*}
   (z_1 – z_2)(1+z_3\overline{z_3}) = (z_1 – z_3)(1+z_2\overline{z_3}) + (z_3 – z_2)(1+z_1\overline{z_3}).
   \end{equation*}
9. Sean $z,w\in\mathbb{C}$ y sea $n\in\mathbb{N}$. Prueba el siguiente resultado:
   \begin{equation*}
   (n+zw)(n+\overline{zw}) \leq \left(n+|\,z\,|^2\right) \left(n+|\,w\,|^2\right). \end{equation*}

Más adelante…

Hasta ahora hemos realizado una interpretación geométrica de los números complejos mediante una correspondencia con los puntos del plano, ahora llamado el plano complejo. Analizamos las operaciones aritméticas de estos números y notamos cómo la suma y resta de números complejos se comportan como la suma y resta vectorial en $\mathbb{R}^2$ respectivamente, mientras que notamos que la multiplicación y división de números complejos se comportan como una rotación compuesta con una homotecia en $\mathbb{R}^2$ y la conjugación compleja se comporta como una reflexión del número complejo sobre el eje real. Observamos que la parte real y la parte imaginaria de un número complejo son las proyecciones de dicho número sobre los ejes real e imaginario respectivamente.

De manera geométrica interpretamos el concepto del módulo de un número complejo como la distancia que hay entre un número $z\in\mathbb{C}$ y el cero. Además probamos algunas propiedades del módulo que nos permitieron caracterizar y entender mejor a los números complejos. Por ejemplo, notamos que en el caso en que un número complejo es un número real entonces el módulo de $\mathbb{C}$ es simplemente el valor absoluto de $\mathbb{R}$ y que a diferencia de $\mathbb{R}$, en $\mathbb{C}$ no es posible establecer un orden que sea compatible con las operaciones de campo definidas en la entrada anterior.

En la siguiente entrada continuaremos analizando al campo $\mathbb{C}$ desde una perspectiva geométrica. Consideraremos el concepto del módulo y sus propiedades para dar una nueva interpretación de un número complejo mediante el uso de coordenadas polares, misma que nos permitirá dar solución a ecuaciones de la forma $w^n = z$, con $w,z\in\mathbb{C}$, $z\neq 0$ y $n\in\mathbb{Z}$.

Entradas relacionadas

• Ir a Variable Compleja I.
• Entrada anterior del curso: El campo de los números complejos.
• Siguiente entrada del curso: Forma Polar. Potencias en $\mathbb{C}$.