$\mathit{\text{MATERIAL EN REVISIÓN}}$

Introducción

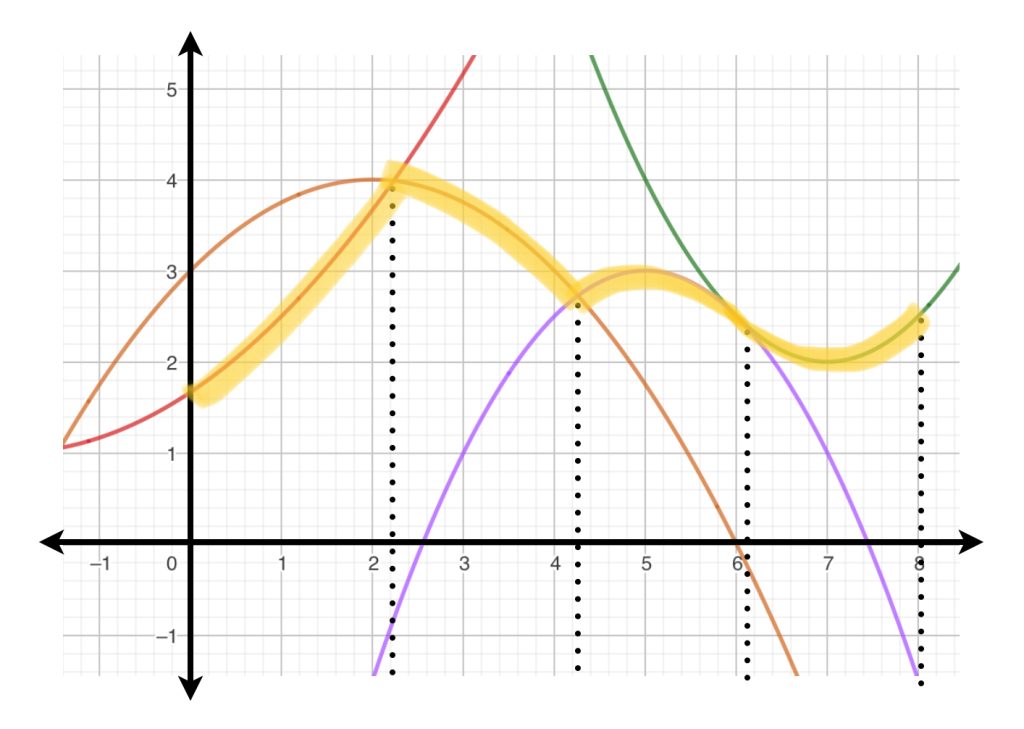
En las entradas anteriores vimos que es posible aproximarnos a una función continua a través de polinomios (link Bernstein) y también que es posible generalizar el concepto en funciones continuas con dominio en un espacio compacto (link Stone-Weierstrass). No queremos pasar a otra sección sin hacer notar que, para el caso de las funciones continuas en un intervalo cerrado, también es posible encontrar una aproximación a través de una función cuadrática por pedazos.

Definición. Función cuadrática por pedazos. Sea $[a,b]\subset \mathbb{R},$ decimos que $f:[a,b]\to \mathbb{R}$ es una función cuadrática por pedazos en $[a,b]$ si existen intervalos $[x_0=a,x_1],[x_1,x_2],\dots ,[x_n-1,x_n=b]$ donde $x_{i-1}<x_i,i=1,\dots ,n$ tal que la función $f$ restringida en cada intervalo $[x_{i-1},x_i]$ es una función cuadrática.

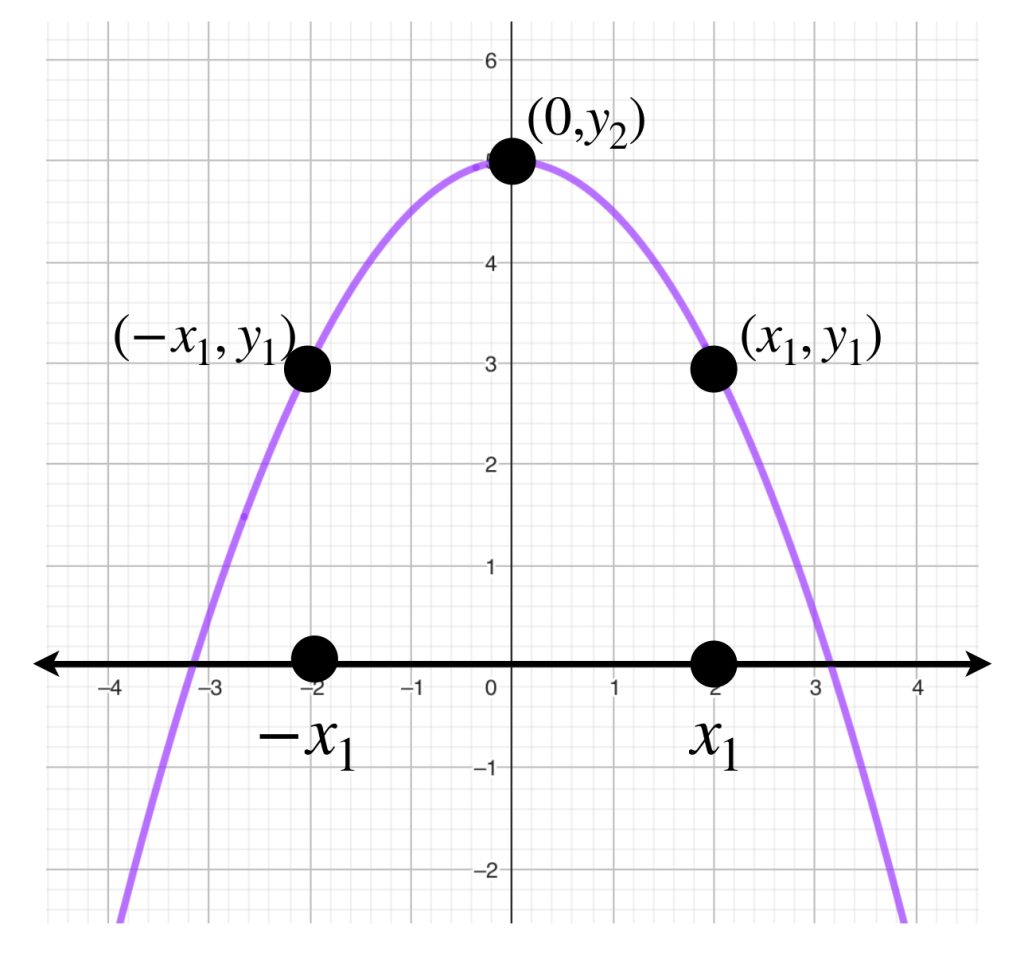
Antes de dar paso a la proposición recordemos que si tenemos tres puntos $P_1(-x_1,y_1),P_2(0,y_2),P_3(x_1,y_1)$ con $x_1,y_1,y_2\in \mathbb{R}$ como muestra la imagen, entonces la parábola que pasa por ellos tiene a $P_2$ como vértice de la parábola y por tanto también como máximo o mínimo.

Dicha parábola está dada por la función $P(x)=\left({\displaystyle \frac{y_1–y_2}{x_1^2}}\right)x^2+y_2.$

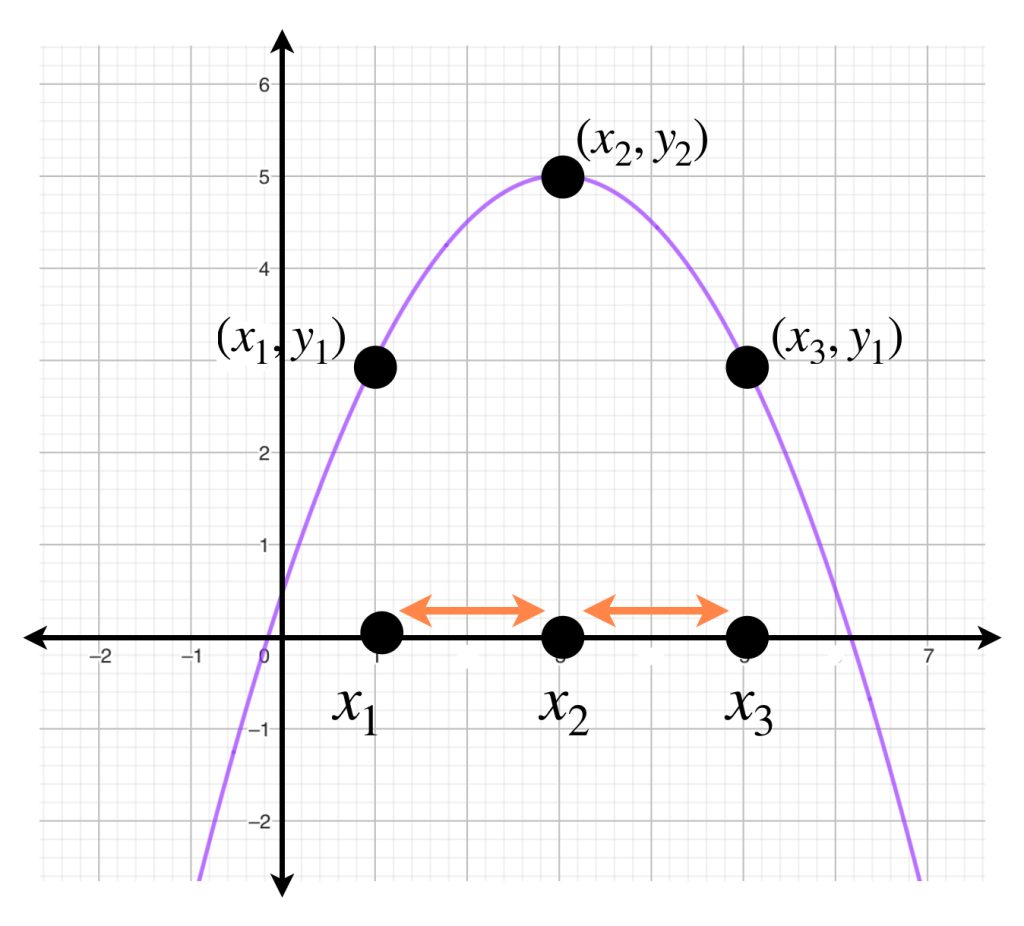
Una traslación nos muestra que esta propiedad se cumple para cualesquiera tres puntos del plano cuando uno de ellos tiene la primera coordenada en el punto medio de las primeras coordenadas de los otros dos.

Esta construcción la usaremos más adelante. Ahora sí, demos paso a la aproximación deseada.

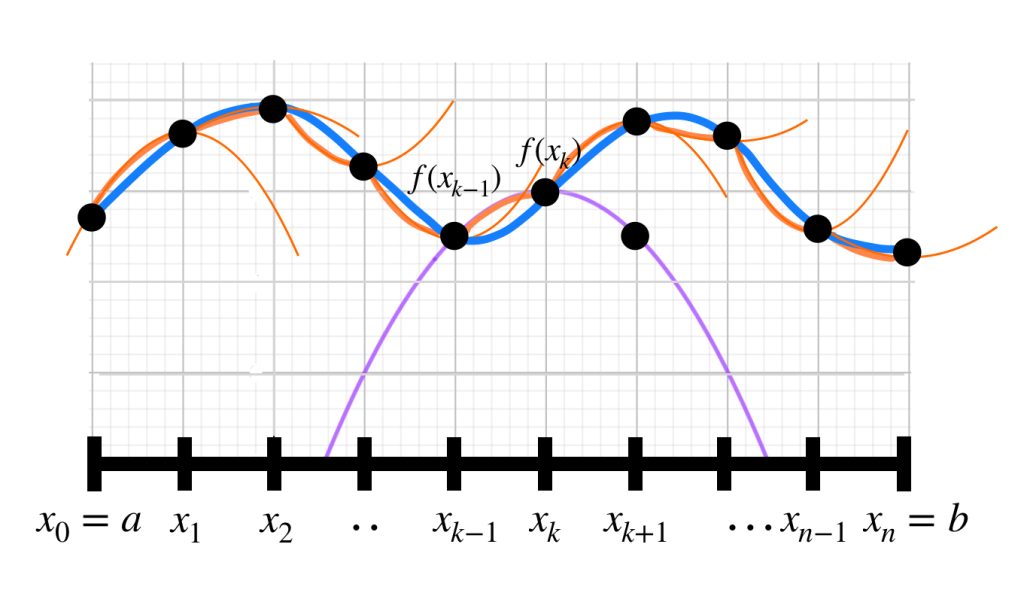
Proposición: Sea $A$ el conjunto de las funciones cuadráticas por pedazos en el intervalo $[a,b]\subset \mathbb{R},$ entonces $A$ es denso en ${\mathcal{C}}^0([a,b],\mathbb{R}\mathbb{)}$ (el conjunto de las funciones continuas en $[a,b]$).

Demostración:
Sea $f\in {\mathcal{C}}^0([a,b],\mathbb{R}\mathbb{)}$ y $\epsilon >0.$ Para probar que $A$ es denso en ${\mathcal{C}}^0([a,b],\mathbb{R}\mathbb{)},$ buscamos $g\in A$ tal que
$$d_{\mathrm{\infty }}(f,g)<\epsilon .$$

Como $f$ es continua en $[a,b]$ entonces también es uniformemente continua, por lo tanto existe $\delta >0$ tal que para cada $x,y\in [a,b],$ si $|x-y|<\delta$ entonces
$$\begin{array}{}\text{(1)}& |f(x)–f(y)|<{\displaystyle \frac{\epsilon }{2}}.\end{array}$$

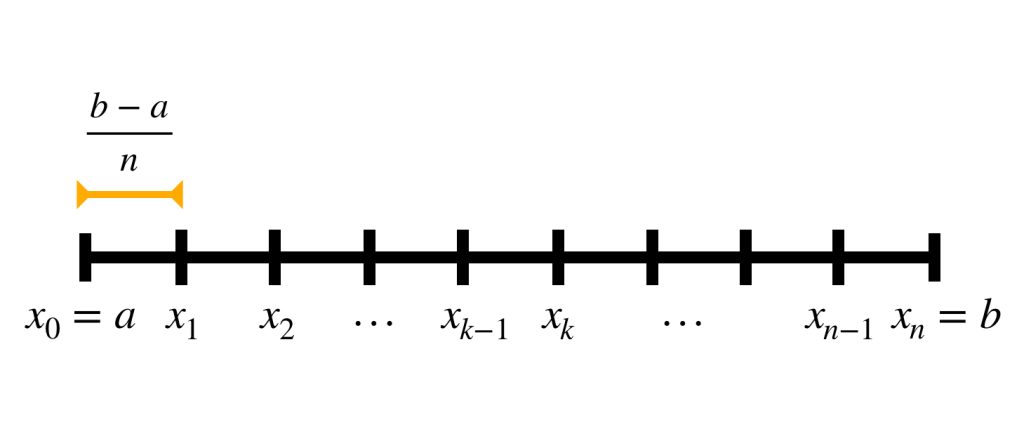
Sea $n\in \mathbb{N}$ tal que ${\displaystyle \frac{b-a}{n}}<\delta$

Definimos $n$ intervalos de longitud ${\displaystyle \frac{b-a}{n}}$ en $[a,b]$ como sigue:

$[a,a+{\displaystyle \frac{b-a}{n}}],[a+{\displaystyle \frac{b-a}{n}},a+2{\displaystyle \frac{b-a}{n}}],\dots ,[a+(n-1){\displaystyle \frac{b-a}{n}},a+n{\displaystyle \frac{b-a}{n}}=b]$

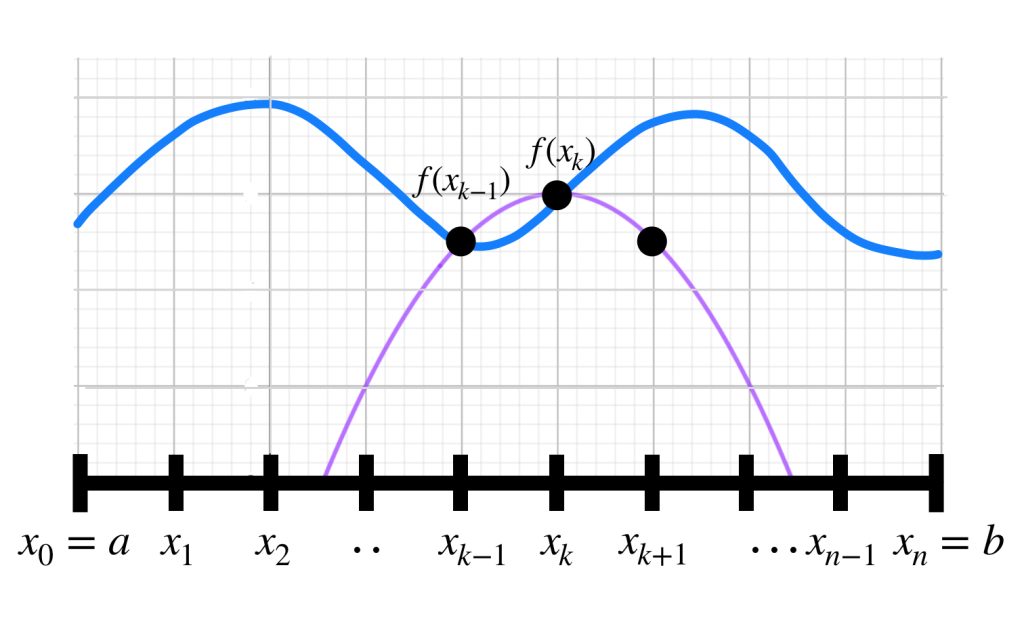
Si $x_k=a+k{\displaystyle \frac{b-a}{n}},$ $k=0,\dots ,n,$ para cada intervalo $[x_{k-1},x_k]$ con $k=1,\dots ,n$ identifica la parábola que pasa por el punto $(x_{k-1},f(x_{k-1})),$ el punto $(x_k,f(x_k))$ (motivados por la función $f$) y el punto $(x_k+\frac{b-a}{n},f(x_{k-1}))$ (simplemente reflejando al punto $(x_{k-1},f(x_{k-1})$ en la recta $x=x_k$ ).

Arriba describimos que existe una parábola $g_k$ que pasa por esos tres puntos y que hace que el punto $(x_k,f(x_k))$ sea vértice y así es también máximo o mínimo de la parábola. Consideremos únicamente la restricción de $g_k$ en el intervalo $[x_{k-1},x_k]$ y una concatenación de estas para definir una función $g,$ es decir

$$g(x):=\sum _{k=1}^n{1}_{[x_{k-1},x_k]}{g}_k(x)$$

donde $1_{[x_{k-1},x_k]}$ es la función característica en el intervalo $[x_{k-1},x_k]$.

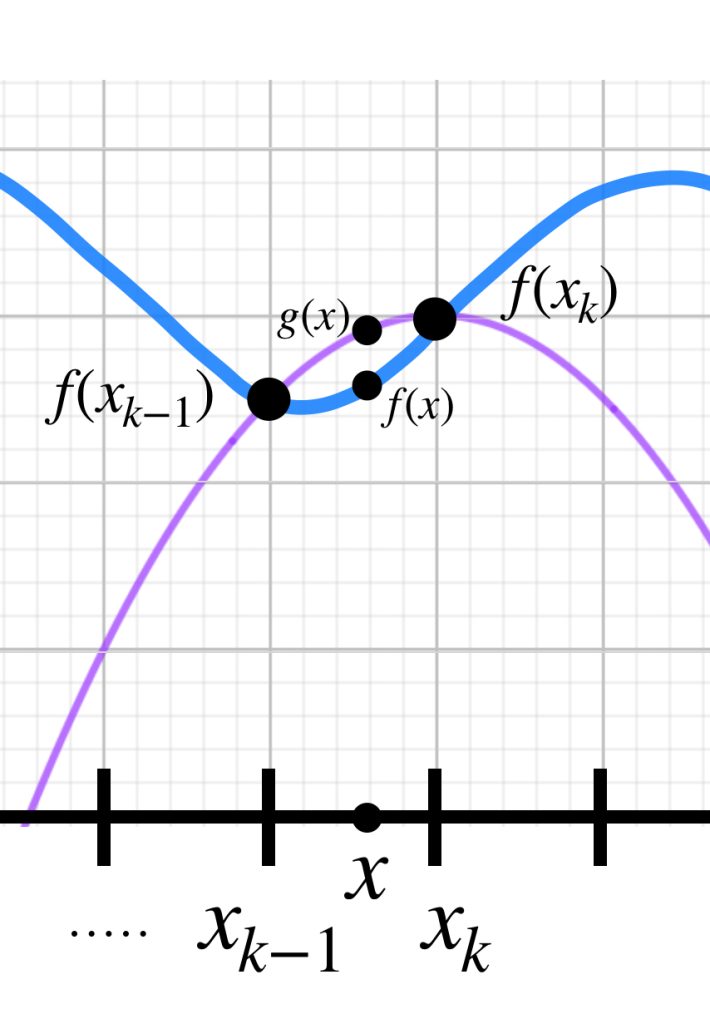
Ahora probemos que la distancia de $f$ a $g$ es menor que $\epsilon .$ Sea $x\in [a,b],$ entonces $x\in [x_{k-1},x_k]$ para algún $k\in \{1,\dots ,n\}.$

Por (1) sabemos que
$$|x–x_k|<\delta \Rightarrow |f(x)–f(x_k)|<\frac{\epsilon }{2}$$

Por otro lado, como $g$ es creciente cuando $f(x_k)$ es máximo (o decreciente si es mínimo), entonces se cumple

$$\begin{array}{rlrl}& & f(x_{k-1})=g(x_{k-1})\le & g(x)\le g(x_k)=f(x_k)\\ & \text{o bien }& f(x_k)=g(x_k)\le & g(x)\le g(x_{k-1})=f(x_{k-1}),\end{array}$$

En cualquier caso $|f(x_k)–g(x)|<\frac{\epsilon }{2}$

Por lo tanto

$$|f(x)–g(x)|\le |f(x)–f(x_k)|+|f(x_k)–g(x)|<\frac{\epsilon }{2}+\frac{\epsilon }{2}=\epsilon$$

probando así que

$$d_{\mathrm{\infty }}(f,g)<\epsilon .$$

Más adelante…

Comenzaremos con la última sección del blog correspondiente a Análisis Matemático I. A través de definiciones y proposiciones llegaremos al concepto de la integral de Riemann-Stieltjes. Esta noción generaliza a la integral de Riemann, que suele verse en los cursos de Cálculo, pero que también es un caso particular de la integral de Lebesgue, la que se verá en el curso de Análisis Matemático II.

Tarea moral

1. Sea $[a,b]\in \mathbb{R}$ y sea $A$ el conjunto de funciones lineales por pedazos en $[a,b].$ Muestra que $A$ es denso en ${\mathcal{C}}^0([a,b],\mathbb{R}).$

Enlaces

• Análisis Matemático.
• Enlace a entrada anterior.
• Enlace a entrada siguiente.