Introducción
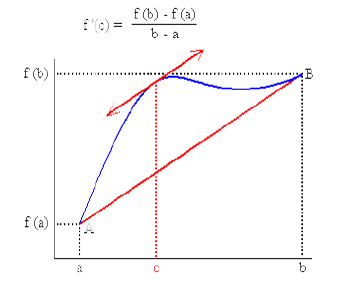
El Teorema del valor medio es un resultado fundamental del cálculo diferencial. En cálculo de una variable nos dice que en algún punto del intervalo, la pendiente de la tangente a la curva (es, decir la derivada) es igual a la pendiente de la recta secante que une los puntos extremos $(a,f(a))$ y $(b,f(b))$. En esta sección estudiaremos para el caso en más dimensiones.
Recordemos el teorema del valor medio para funciones de $\mathbb{R}\rightarrow \mathbb{R}$
Suponga que $f:[a,b]\rightarrow\mathbb{R}$ es derivable en $(a,b)$ y continua en $[a,b]$ entonces existe $c\in(a,b)$ tal que
$$f'(c)=\frac{f(b)-f(a)}{b-a}$$
En esta sección se presenta el caso en la versión para funciones de $\mathbb{R}^{n}$ en $\mathbb{R}$. De esta manera el caso general se ve de la siguiente manera:
Teorema. Sea $f:A\subset\mathbb{R}^{n} \rightarrow \mathbb{R}$
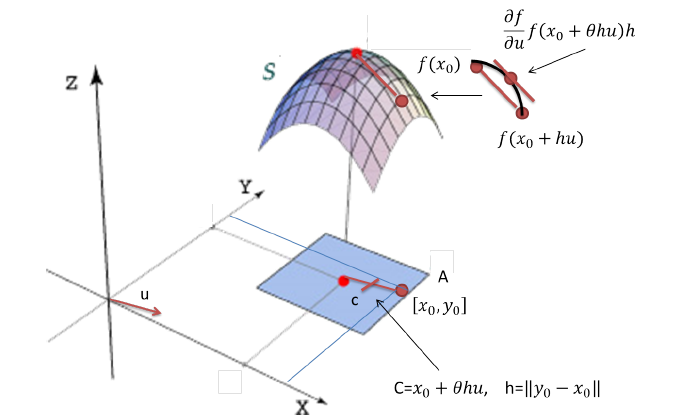
una función definida en el conjunto abierto $A$ de $\mathbb{R}^{n}$. Si $x_{0},y_{0} \in A$ se pide que el conjunto $A$ sea tal que $[x_0,y_0]=\left\{x_{0}+t(y_{0}-x_{0})~|~t\in[0,1]\right\}\subset A$. Sea $u$ un vector unitario en la dirección del vector $y_{0}-x_{0}$. Si la función $f$ es continua en los puntos del segmento $[x_0,y_0]$ y
tiene derivadas direccionales en la dirección del vector $u$ en los puntos del segmento $(x_0,y_0)$, entonces existe $\theta$ , $0<\theta<1$ tal que $f(x_0+hu)-f(x_0)=\displaystyle\frac{\partial f}{\partial u}(x_0+\theta
hu)h$ donde $h=|y_0-x_0|$.
Una consecuencia del teorema anterior es el teorema
Teorema. Sea $f:A\subset\mathbb{R}^{n} \rightarrow \mathbb{R}$
una función definida en el conjunto abierto $A$ de $\mathbb{R}^{n}$. Si las derivadas parciales $\displaystyle{\frac{\partial f}{\partial x_{i}}~~\forall i=1,..,n}$ son continuas en $x_{0}\in A$ entonces f es diferenciable en $x_{0}\in A$
Vamos a dar una idea de la demostración para el caso n=2
Teorema del Valor Medio para Funciones de $\mathbb{R}^{2}\rightarrow \mathbb{R}$
Teorema. Sea $f:A\subset\mathbb{R}^{2} \rightarrow \mathbb{R}$ una función definida en el conjunto abierto $A$ de $\mathbb{R}^{2}$. Si $x_{0},y_{0} \in A$ se pide que el conjunto $A$ sea tal que $[x_0,y_0]=\left\{x_{0}+t(y_{0}-x_{0})~|~t\in[0,1]\right\}\subset A$. Sea $u$ un vector unitario en la dirección del vector $y_{0}-x_{0}$. Si la función
$f$ es continua en los puntos del segmento $[x_0,y_0]$ y tiene derivadas direccionales en la dirección del vector $u$ en los puntos del segmento $(x_0,y_0)$, entonces existe
$\theta$ \, $0<\theta<1$ tal que $f(x_0+hu)-f(x_0)=\displaystyle\frac{\partial f}{\partial u}(x_0+\theta hu)h$ donde $h=|y_0-x_0|$.
Demostración. Considere la función $\phi:[0,h]\rightarrow
\mathbb{R}$ dada por $\phi(t)=f(x_0+tu)$ ciertamente
la función $\phi$ es continua en $[0,h]$ pues $f$ lo es en $[x_0,y_0]$. Ademas
[\begin{array}{ll}
\phi'(t) & =\displaystyle\lim_{h \rightarrow 0}
\frac{\phi(t+h)-\phi(t)}{h} \\
\, & = \displaystyle\lim_{h \rightarrow 0}
\frac{f(x_0+(t+h)u)-f(x_0+tu)}{h} \\
\, & = \displaystyle\lim_{h \rightarrow 0}
\frac{f(x_0+tu+hu)-f(x_0+tu)}{h} \\
\, & = \displaystyle\frac{\partial f}{\partial
u}(x_0+tu)
\end{array}]
de modo que para $t \in (0,h)$, $\phi'(t)$ existe y es la derivada direccional de $f$ en $x_0+tu \in (x_0,y_0)$ en la dirección del vector $u$. Aplicando entonces el teorema del valor medio a la función $\phi$, concluimos que existe un múmero $\theta \in (0,1)$ que da $\phi(h)-\phi(0)=\phi'(\theta h)h$\ es decir de modo que $$f(x_0+hu)-f(x_0)=\frac{\partial f}{\partial u}(x_0+\theta hu)h$$
Ahora para la verisón del teorema 3
Teorema 5. Sea $f:A\subset\mathbb{R}^{2} \rightarrow \mathbb{R}$
una función definida en el conjunto abierto $A$ de $\mathbb{R}^{n}$. Si las derivadas parciales $\displaystyle{\frac{\partial f}{\partial x},~~\frac{\partial f}{\partial y}}$ son continuas en $(x_{0},y_{0})\in A$ entonces f es diferenciable en $(x_{0},y_{0}\in A$
Demostración. Vamos a probar que $$f((x_{0},y_{0})+(h_{1},h_{2}))=f(x_{0},y_{0})+\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}+r(h_{1},h_{2})$$donde $$\lim_{(h_{1},h_{2})\rightarrow(0,0)}\frac{r(h_{1},h_{2})}{|(h_{1},h_{2})|}=0$$
para ello tenemos que
$$r(h_{1},h_{2})=f((x_{0},y_{0})+(h_{1},h_{2}))-f(x_{0},y_{0})-\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}-\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}$$
sumando un cero adecuado
$$r(h_{1},h_{2})=f((x_{0},y_{0})+(h_{1},h_{2}))-\textcolor{Red}{f(x_{0},y_{0}+h_{2})}+\textcolor{Red}{f(x_{0},y_{0}+h_{2})}-f(x_{0},y_{0})-\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}-\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}$$
trabajaremos
$$f((x_{0},y_{0})+(h_{1},h_{2}))-\textcolor{Red}{f(x_{0},y_{0}+h_{2})}$$Considerando la función $\varphi(x)=f(x,y_{0}+h_{2})$ por lo tanto tenemos que $$\varphi'(x)=\lim_{h_{1}\rightarrow0}\frac{\varphi(x+h_{1})-\varphi(x)}{h_{1}}=\lim_{h_{1}\rightarrow0}\frac{f(x+h_{1},y_{0}+h_{2})-f(x,y_{0}+h_{2})}{h_{1}}$$
este limite existe y nos dice que $\varphi$ es es continua en este caso en el intervalo $[x_{0},x_{0}+h_{1}]$. Por lo tanto aplicando el TVM en dicho intervalo se obtiene
$$\varphi(x_{0}+h_{1})-\varphi(x_{0})=\varphi'(x_{0}+\theta_{1} h_{1})h_{1}~p.a.~\theta_{1}\in(0,1)$$
es decir
$$f((x_{0}+h_{1},y_{0}+h_{2})-\textcolor{Red}{f(x_{0},y_{0}+h_{2})}=\frac{\partial f}{\partial x}(x_{0}+\theta_{1} h_{1},y_{0}+h_{2})h_{1}$$
Analogamente
$$\textcolor{Red}{f(x_{0},y_{0}+h_{2})}-f(x_{0},y_{0})$$Considerando la función $\varphi(y)=f(x_{0},y)$ por lo tanto tenemos que $$\varphi'(y)=\lim_{h_{2}\rightarrow0}\frac{\varphi(x_{0},y_{0}+h_{2})-\varphi(y_{0}+h_{2})}{h_{2}}=\lim_{h_{2}\rightarrow0}\frac{f(x_{0},y_{0}+h_{2})-f(y_{0}+h_{2})}{h_{2}}$$
este limite existe y nos dice que $\varphi$ es es continua en este caso en el intervalo $[y_{0},y_{0}+h_{2}]$. Por lo tanto aplicando el TVM en dicho intervalo se obtiene
$$\varphi(y_{0}+h_{2})-\varphi(y_{0})=\varphi'(y_{0}+\theta_{2} h_{2})h_{2}~p.a.~\theta_{2}\in(0,1)$$
es decir
$$f((x_{0},y_{0}+h_{2})-\textcolor{Red}{f(x_{0},y_{0})}=\frac{\partial f}{\partial y}(x_{0},y_{0}+\theta_{2}h_{2})h_{2}$$
Sustituimos en
$$r(h_{1},h_{2})=f((x_{0},y_{0})+(h_{1},h_{2}))-\textcolor{Red}{f(x_{0},y_{0}+h_{2})}+\textcolor{Red}{f(x_{0},y_{0}+h_{2})}-f(x_{0},y_{0})-\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}-\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}$$y obtenemos
$$r(h_{1},h_{2})=\frac{\partial f}{\partial x}(x_{0}+\theta_{1} h_{1},y_{0}+h_{2})h_{1}-\frac{\partial f}{\partial x}(x_{0},y_{0})h_{1}+\frac{\partial f}{\partial y}(x_{0},y_{0}+\theta_{2}h_{2})h_{2}-\frac{\partial f}{\partial y}(x_{0},y_{0})h_{2}$$
es decir
$$r(h_{1},h_{2})=\left(\frac{\partial f}{\partial x}(x_{0}+\theta_{1} h_{1},y_{0}+h_{2})-\frac{\partial f}{\partial x}(x_{0},y_{0})\right)h_{1}+\left(\frac{\partial f}{\partial y}(x_{0},y_{0}+\theta_{2}h_{2})-\frac{\partial f}{\partial y}(x_{0},y_{0})\right)h_{2}$$
por lo tanto
$$\frac{r(h_{1},h_{2})}{|(h_{1},h_{2})|}=\left(\frac{\partial f}{\partial x}(x_{0}+\theta_{1} h_{1},y_{0}+h_{2})-\frac{\partial f}{\partial x}(x_{0},y_{0})\right)\frac{h_{1}}{|(h_{1},h_{2})|}+\left(\frac{\partial f}{\partial y}(x_{0},y_{0}+\theta_{2}h_{2})-\frac{\partial f}{\partial y}(x_{0},y_{0})\right)\frac{h_{2}}{|(h_{1},h_{2})|}$$
ahora bien si $\displaystyle{|(h_{1},h_{2})|\rightarrow(0,0)}$ se tiene
$$\left(\frac{\partial f}{\partial x}(x_{0}+\theta_{1} h_{1},y_{0}+h_{2})-\frac{\partial f}{\partial x}(x_{0},y_{0})\right)\rightarrow0$$
y
$$\frac{h_{1}}{|(h_{1},h_{2})|}<1$$
Analogamente
$$\left(\frac{\partial f}{\partial y}(x_{0},y_{0}+\theta_{2}h_{2})-\frac{\partial f}{\partial y}(x_{0},y_{0})\right)\rightarrow0$$
y
$$\frac{h_{2}}{|(h_{1},h_{2})|}<1$$
en consecuencia
$$\lim_{(h_{1},h_{2})\rightarrow(0,0)}\frac{r(h_{1},h_{2})}{|(h_{1},h_{2})|}=0$$por lo tanto f es diferenciable en $(x_{0},y_{0})$
Más adelante
Estudiremos la definición del vector gradiente, el cual, contiene las derivadas parciales de una función real y veremos su importancia en relación a una dirección (vector) dado para analizar el crecimiento de una función.
Tarea Moral
Mostrar que la siguiente función es diferenciable en cada punto de su dominio.
1.- $f(x,y)= \displaystyle{\dfrac{2xy}{(x^2+y^2)^2}}$
2.-$f(x,y)=\dfrac{x}{y}+\dfrac{y}{x}$
3.-$f(r,\theta)=\dfrac{1}{2}rsen2\theta$, $r>0$
4.-$f(x,y)=\dfrac{xy}{\sqrt{x^2+y^2}}$
5.-$f(x,y)=\dfrac{x^2y}{x^4+y^2}$