Introducción

En la entrada anterior trabajamos con la ecuación diferencial ${\displaystyle \frac{dy(x)}{dx}}=y(x)$ con condición inicial $y(0)=1.$ Al identificar propiedades enunciadas en el teorema de punto fijo de Banach encontramos su solución. En esta ocasión repetiremos el proceso para demostrar que la solución a una ecuación diferencial general existe y es única.

Primeramente, veamos un concepto.

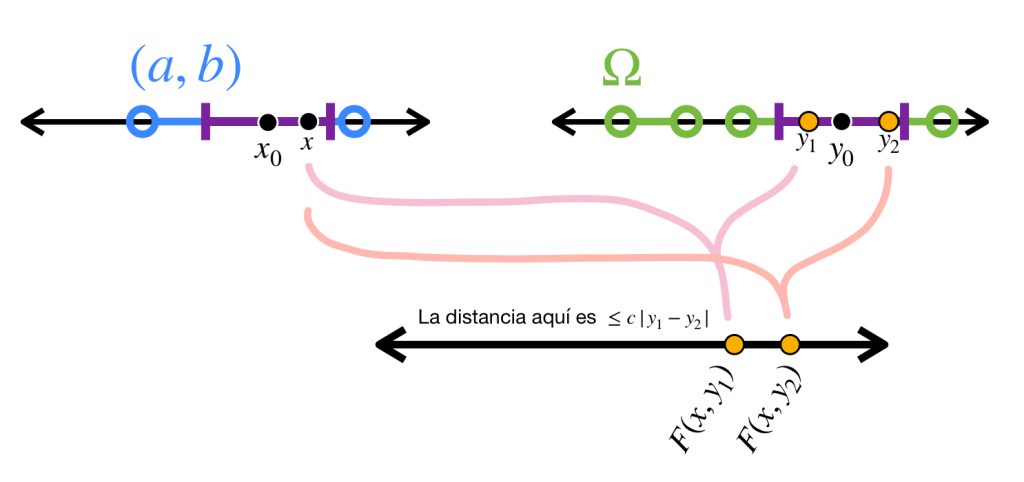
Definición. Función localmente Lipschitz continua en la segunda variable. Sea $(a,b)\subset \mathbb{R}$ y sea $\mathrm{\Omega }\subset \mathbb{R}$ tal que $\mathrm{\Omega }$ es abierto. Si $F:(a,b)\times \mathrm{\Omega }\to \mathbb{R}$ es una función que satisface que para cada $x_0\in (a,b)$ y $y_0\in \mathrm{\Omega }$ existen ${\delta }_0>0$ y $c>0$ tales que $[x_0–{\delta }_0,x_0+{\delta }_0]\subset (a,b),[y_0–{\delta }_0,y_0+{\delta }_0]\subset \mathrm{\Omega }$ y además que si $x\in [x_0–{\delta }_0,x_0+{\delta }_0]$ y si $y_1,y_2\in [y_0–{\delta }_0,y_0+{\delta }_0]$ entonces
$$|F(x,y_1)-F(x,y_2)|\le c|y_1-y_2|$$
diremos que $F$ es localmente Lipschitz continua en la segunda variable.

Solución a la ecuación diferencial ${\displaystyle \frac{dy(x)}{dx}}=F(x,y(x))$

Sea ${\displaystyle \frac{dy(x)}{dx}}=F(x,y(x))$ una ecuación diferencial con condición inicial $y(x_0)=y_0$ donde:

1. $F$ es una función localmente Lipschitz continua en la segunda variable.
2. $y$ es una función, al menos derivable, de variable $x$ que manda valores reales en valores reales.
3. $x_0$ es un punto donde la $y$ buscada toma valor $y_0.$

Plan para resolverla con el teorema de punto fijo de Banach: Propondremos un espacio métrico completo $(X,d)$ de funciones entre las cuales deberá estar la $y$ buscada y una contracción $\varphi :X\to X$ cuyo punto fijo sea la solución de la ecuación diferencial.

Sean ${\delta }_0>0$ y $c>0$ para $F$ localmente Lipschitz continua como en la definición. Se dejará como ejercicio al lector probar que $F$ restringida en $[x_0–{\delta }_0,x_0+{\delta }_0]\times [y_0–{\delta }_0,y_0+{\delta }_0]$ es continua. Como este conjunto es compacto, se sigue que $F$ está acotada en este conjunto. Por lo tanto existe $M>0$ tal que para toda $(x,y)\in [x_0–{\delta }_0,x_0+{\delta }_0]\times [y_0–{\delta }_0,y_0+{\delta }_0]$ se cumple
$$|f(x,y)|\le M.$$

Sea $\delta$ tal que $0<\delta <min\{\frac{1}{c},\frac{{\delta }_0}{M}\}$

Considera $X:=\{f\in {\mathcal{C}}^0([x_0–\delta ,x_0+\delta ],\mathbb{R}):d_{\mathrm{\infty }}(f,y_0)\le \delta M\}$
donde $y_0$ representa, en este caso, a la función constante que arroja el valor $y_0.$ Nota que $X$ es un espacio cerrado en el espacio métrico ${\mathcal{C}}^0([x_0–\delta ,x_0+\delta ],\mathbb{R})$ que recordemos, tiene la propiedad de ser completo. Por lo visto en la última proposición de la entrada Espacios métricos completos concluimos que $X$ también es completo.

Propongamos la contracción $\varphi$ deseada

Si $f\in X$ satisface la ecuación diferencial entonces para todo $x\in [x_0–\delta ,x_0+\delta ]$ se sigue:

$$\begin{array}{rlrl}& & {\displaystyle \frac{df(x)}{dx}}& =F(x,f(x))\\ & \Rightarrow & {\int }_{x_0}^x{\displaystyle \frac{df(t)}{dt}}dt& ={\int }_{x_0}^{x}F(t,f(t))dt\\ & \Rightarrow & f(x)–f(x_0)& ={\int }_{x_0}^{x}F(t,f(t))dt\\ & \Rightarrow & f(x)& =f(x_0)+{\int }_{x_0}^{x}F(t,f(t))dt\\ & \Rightarrow & f(x)& =y_0+{\int }_{x_0}^{x}F(t,f(t))dt\end{array}$$

Como buscamos que esta solución sea punto fijo de una contracción $\varphi$ en $X$ entonces $\varphi (f(x))=f(x).$ La última igualdad nos lleva a proponer:

$$\varphi (f(x)):=y_0+{\int }_{x_0}^{x}F(t,f(t))dt$$

Nota que $\varphi (f(x))$ pertenece a ${\mathcal{C}}^0([x_0–\delta ,x_0+\delta ],\mathbb{R}).$ Probaremos que también pertenece a $X.$ Si $x\in [x_0–\delta ,x_0+\delta ],$ tenemos dos casos:

De ambos casos podemos concluir que $d_{\mathrm{\infty }}(f,y_0)\le \delta M,$ por lo tanto $\varphi (f)\in X.$

$\varphi$ es contracción en $X$

Sean $f,g\in X.$ Considera $I=[x_0–\delta ,x_0+\delta ]$ entonces si $x\in I,$ tenemos dos casos.

Si $x<x_0.$

$$\begin{array}{rl}|\varphi (f(x))-\varphi (g(x))|& =|y_0+{\int }_{x_0}^{x}F(t,f(t))dt-(y_0+{\int }_{x_0}^{x}F(t,g(t))dt)|\\ & =|{\int }_{x_0}^{x}F(t,f(t))dt-F(t,g(t))dt|\\ & =|-{\int }_x^{x_0}F(t,f(t))dt-F(t,g(t))dt|\\ & =|{\int }_x^{x_0}F(t,f(t))dt-F(t,g(t))dt|\\ & \le {\int }_x^{x_0}|F(t,f(t))dt-F(t,g(t))|dt\\ & \le {\int }_x^{x_0}c|f(t)-g(t)|dt\\ & \le (x_0-x)c{d}_{\mathrm{\infty }}(f,g)\\ & \le (\delta c)d_{\mathrm{\infty }}(f,g)\end{array}$$

Por lo tanto, la distancia entre $\varphi (f)$ y $\varphi (g)$ se puede estimar como

$$\begin{array}{rl}{d}_{\mathrm{\infty }}(\varphi (f(x)),\varphi (g(x)))& =\underset{x\in I}{Sup}\{|\varphi (f(x))-\varphi (g(x))|\}\\ & \le \underset{x\in I}{Sup}\{\delta c{d}_{\mathrm{\infty }}(f,g)\}\\ & =(\delta c)d_{\mathrm{\infty }}(f,g)\end{array}$$

Sea $\alpha :=\delta c$ entonces $\alpha <1,$ por lo tanto $\varphi$ es contracción en $X.$

Lo que hemos visto en esta entrada demuestra el siguiente:

Teorema. Picard-Lindelöf. Sea $F:(a,b)\times \mathrm{\Omega }\to \mathbb{R}$ una función continua y localmente Lipschitz continua en la segunda variable. Entonces, dados $x_0\in (a,b)$ y $y_0\in \mathrm{\Omega }$ existe $\delta >0$ tal que la ecuación diferencial
$${\displaystyle \frac{dy(x)}{dx}}=F(x,y(x)),y(x_0)=y_0$$
tiene una única solución en el intervalo $[x_0–\delta ,x_0+\delta ].$

Generalización en ${\mathbb{R}}^n$

Si $\mathrm{\Omega }\subset {\mathbb{R}}^n$ y $F$ tiene su contradominio en ${\mathbb{R}}^n$ entonces la definición y el teorema quedan como sigue:

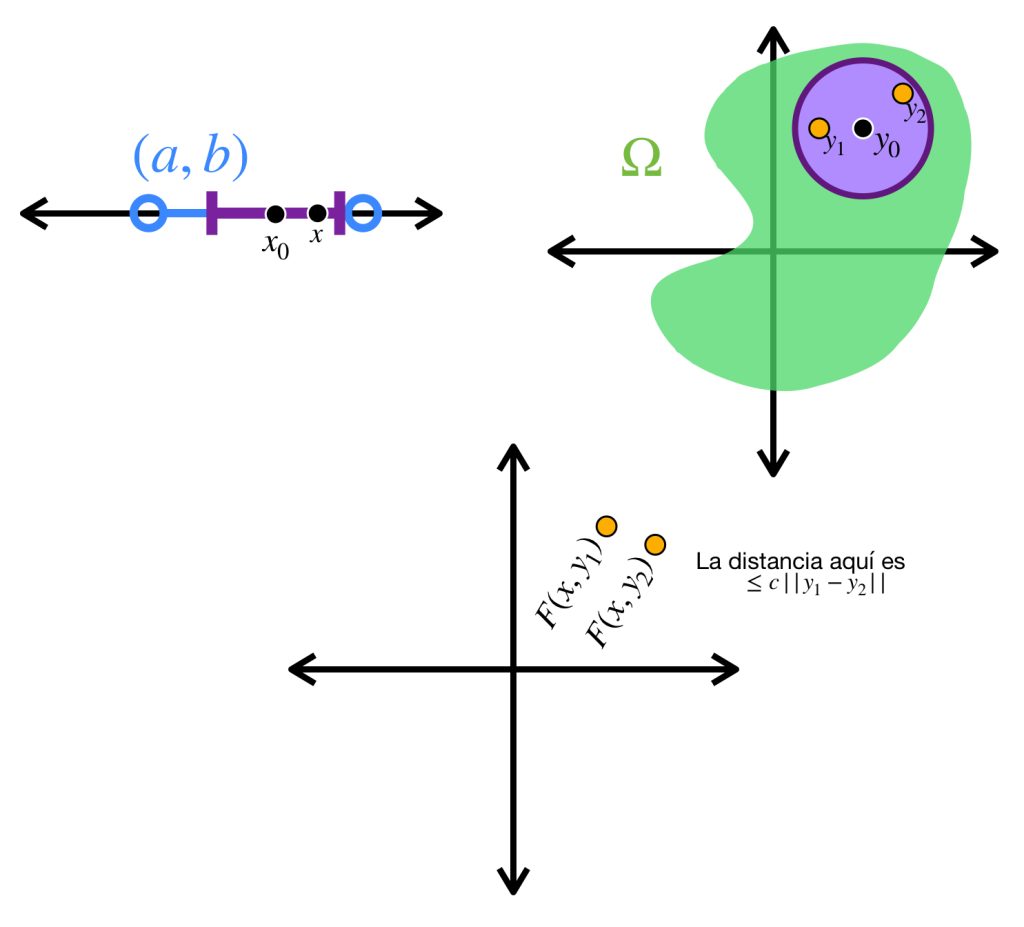
Definición. Función localmente Lipschitz continua en la segunda variable. Sea $(a,b)\subset \mathbb{R}$ y sea $\mathrm{\Omega }\subset {\mathbb{R}}^n$ tal que $\mathrm{\Omega }$ es abierto. Si $F:(a,b)\times \mathrm{\Omega }\to {\mathbb{R}}^n$ es una función que satisface que para cada $x_0\in (a,b)$ y $y_0\in \mathrm{\Omega }$ existen ${\delta }_0>0$ y $c>0$ tales que $[x_0–{\delta }_0,x_0+{\delta }_0]\subset (a,b),\bar{B}(y_0,{\delta }_0)\subset \mathrm{\Omega }$ y además que si $|x-x_0|\le {\delta }_0$ y si $y_1,y_2\in \bar{B}(y_0,{\delta }_0)$ entonces
$$\Vert F(x,y_1)-F(x,y_2)\Vert \le c\Vert y_1-y_2\Vert$$
diremos que $F$ es localmente Lipschitz continua en la segunda variable.

Teorema. Picard-Lindelöf. Sea $F:(a,b)\times \mathrm{\Omega }\to {\mathbb{R}}^n$ una función continua y localmente Lipschitz continua en la segunda variable. Entonces, dados $x_0\in (a,b)$ y $y_0\in \mathrm{\Omega }$ existe $\delta >0$ tal que la ecuación diferencial
$${\displaystyle \frac{dy(x)}{dx}}=F(x,y(x)),y(x_0)=y_0$$
tiene una única solución en el intervalo $[x_0–\delta ,x_0+\delta ].$

En este caso el espacio completo donde podemos encontrar la solución es

$$X:=\{f\in {\mathcal{C}}^0([x_0–\delta ,x_0+\delta ],{\mathbb{R}}^n):{\Vert f–y_0\Vert }_{\mathrm{\infty }}\le \delta M\}$$

Donde $\delta$ y $M$ se definen de forma análoga a la demostración anterior.

Más adelante

Pasaremos a la siguiente sección de esta asignatura con temas de compacidad. Aunque ya se han usado algunos resultados para el caso del espacio métrico euclidiano, mostraremos cómo el concepto puede generalizarse en otros espacios a partir de la topología que la métrica induce en ellos.

Tarea moral

1. Sean ${\delta }_0>0$ y $c>0$ para $F$ localmente Lipschitz continua como en la definición. Prueba que $F$ restringida en $[x_0–{\delta }_0,x_0+{\delta }_0]\times [y_0–{\delta }_0,y_0+{\delta }_0]$ es continua.
2. Sea $F:\mathbb{R}\times \mathbb{R}\to \mathbb{R}$ tal que $F(x,y)=3y^{2/3}.$
   a) Prueba que $F$ no es localmente Lipschitz continua en la segunda variable.
   b) Prueba que para cualesquiera $\alpha <0<\beta ,$ la función
   $$f_{\alpha ,\beta }(x)=\{\begin{array}{ll}(x–\alpha {)}^3& \text{si x }\le \alpha ,\\ 0& \text{si }\alpha \le x\le \beta ,\\ (x–\beta {)}^3& \text{si }x\ge \beta .\end{array}$$
   Es diferenciable en $\mathbb{R}$ y es solución de
   $${\displaystyle \frac{dy(x)}{dx}}=3y^{2/3},y(0)=0.$$
   Así, si $F$ no es localmente Lipschitz continua en la segunda variable la ecuación puede tener una infinidad de soluciones.
3. Sea $F:\mathbb{R}\times \mathbb{R}\to \mathbb{R}$ tal que $F(x,y)=-y^2.$
   a) Prueba que $F$ es localmente Lipschitz continua en la segunda variable.
   b) Para $\alpha \ne 0$ considera la ecuación
   $${\displaystyle \frac{dy(x)}{dx}}=-y^2,y(0)=–\frac{1}{\alpha }.$$
   Prueba que $f(x)={\displaystyle \frac{1}{x–\alpha }}$ es su solución en algún intervalo que contiene a $0$.
   c) ¿Cuál es el intervalo máximo para el que esta ecuación tiene solución?

Enlaces

• Análisis Matemático.
• Enlace a entrada anterior.
• Enlace a entrada siguiente.