Archivo de la etiqueta: trayectorias periódicas

Ecuaciones Diferenciales I: Teorema de Poincaré – Bendixson en el plano

Por Omar González Franco

4 respuestas

Una de las cosas más impresionantes sobre las matemáticas es que la gente que
la practica no están normalmente interesadas en su aplicación, porque
las matemáticas en si mismas son una forma de hermoso arte.
– Danica McKellar

Introducción

¡Hemos llegado a la última entrada del curso!

Concluiremos esta unidad con la introducción a un importante teorema de la teoría cualitativa de las ecuaciones diferenciales. El teorema de Poincaré – Bendixson.

La demostración a este teorema suele ser compleja y requiere de definiciones y resultados previos, algunos de ellos sobre topología elemental. En este curso sólo enunciaremos este teorema en una versión simplificada de manera que podamos aplicarlo a los sistemas no lineales de dos ecuaciones diferénciales, por esta razón es que este teorema también se conoce como teorema de Poincaré – Bendixson en el plano.

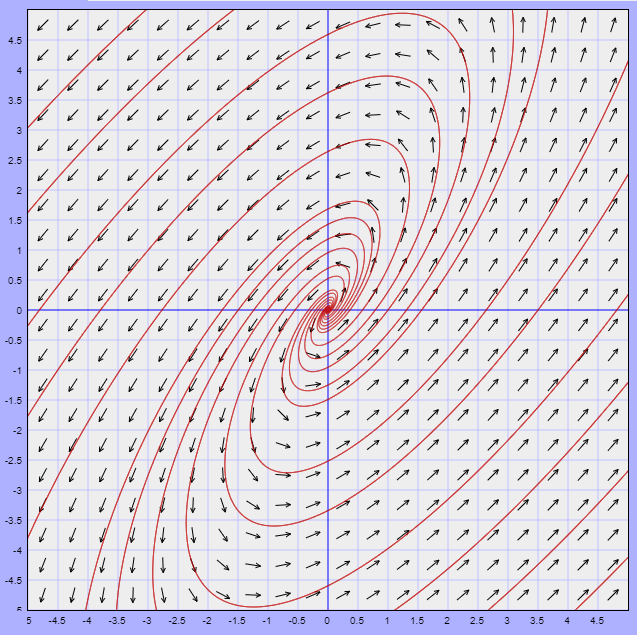
En la entrada sobre linearización visualizamos el plano fase del sistema

\begin{align*}
x^{\prime} &= y \\
y^{\prime} &= -x + \mu(1 -x^{2})y \label{1} \tag{1}
\end{align*}

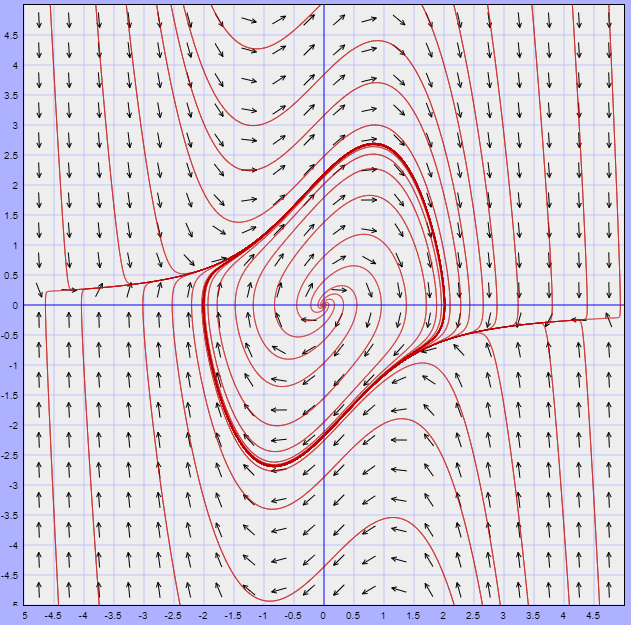
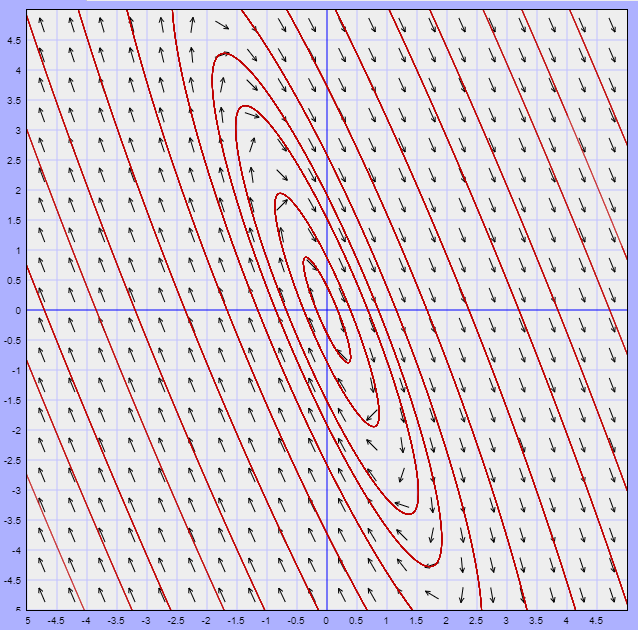
Para el caso en el que $\mu = 1$. Dicho plano fase fue el siguiente.

Plano fase del sistema.

El sistema (\ref{1}) en realidad se deduce de la ecuación diferencial de segundo orden

$$\dfrac{d^{2}y}{dt^2} + \mu(y^{2} -1) \dfrac{dy}{dt}+ y = 0 \label{2} \tag{2}$$

la cual lleva por nombre ecuación de Van der Pol y representa el movimiento de un oscilador con amortiguamiento no lineal.

Lo que podemos observar del plano fase es que existe una trayectoria límite (resaltada en rojo) que de alguna manera divide al plano fase en secciones. Si nos concentramos en la trayectoria periódica formada, entonces podemos hablar de la zona interior y la zona exterior a dicha trayectoria y lo que observamos es que por fuera de ella todas las trayectorias tienden a la trayectoria periódica, mientras que dentro de ella todas se alejan del origen para aproximarse, de igual manera, a la trayectoria límite.

Esto es lo que se conoce como un ciclo límite y lo presentan algunos sistemas no lineales. El teorema de Poincaré – Bendixson nos dará las condiciones necesarias para asegurar que un sistema no lineal presenta ciclos límites.

Antes de continuar haremos un breve paréntesis para recordar un par de resultados importantes de las coordenadas polares que nos servirán para hacer más sencillos los cálculos de los ejemplos que realicemos más adelante.

Coordenadas polares

Las coordenadas cartesianas se relacionan con las polares a través de las siguientes relaciones.

\begin{align*}
x &= r \cos(\theta) \\
y &= r \sin(\theta) \label{3} \tag{3}
\end{align*}

Es claro que

\begin{align*}
r^{2} &= x^{2} + y^{2} \\
\theta &= \arctan \left( \dfrac{y}{x} \right) \label{4} \tag{4}
\end{align*}

Derivemos explícitamente cada una de estas ecuaciones. Por un lado, derivando la ecuación de $r$, se tiene

$$2r \dfrac{dr}{dt} = 2x \dfrac{dx}{dt} + 2y \dfrac{dy}{dt}$$

o bien,

$$r \dfrac{dr}{dt} = x \dfrac{dx}{dt} + y \dfrac{dy}{dt}$$

Utilizando la notación prima, el primer resultado que nos interesa es el siguiente.

$$r r^{\prime} = x x^{\prime} + y y^{\prime} \label{5} \tag{5}$$

Por otro lado, para la ecuación de $\theta$ se tiene

$$\dfrac{d \theta}{dt} = \dfrac{1}{1 + \left( \dfrac{y^{2}}{x^{2}} \right)} \left( \dfrac{x \dfrac{dy}{dt} -y \dfrac{dx}{dt}}{x^{2}} \right) = \dfrac{x \dfrac{dy}{dt} -y \dfrac{dx}{dt}}{x^{2} + y^{2}}$$

Nuevamente usando la notación prima, el segundo resultado que nos interesa es el siguiente.

$$r^{2} \theta^{\prime} = x x^{\prime} -y y^{\prime} \label{6} \tag{6}$$

Las ecuaciones (\ref{5}) y (\ref{6}) nos serán de utilidad a continuación.

Un ciclo límite

Antes de revisar algunos conceptos y de presentar el teorema de Poincaré – Bendixson, consideremos el siguiente sistema no lineal.

\begin{align*}
x^{\prime} &= -y + x(1 -x^{2} -y^{2}) \\
y^{\prime} &= x + y(1 -x^{2} -y^{2}) \label{7} \tag{7}
\end{align*}

Es sencillo hacer notar que el único punto de equilibrio del sistema es el origen $Y_{0} = (0, 0)$.

Utilizando las relaciones (\ref{5}) y (\ref{6}) podemos transformar el sistema en coordenadas polares. Comencemos por obtener la ecuación diferencial para $r$, para ello sustituyamos $x^{\prime}$ y $y^{\prime}$ del sistema (\ref{7}) en la ecuación (\ref{5}).

$$rr^{\prime} = x [-y + x(1 -x^{2} -y^{2})] + y[x + y(1 -x^{2} -y^{2})]$$

Desarrollando, obtenemos

$$r r^{\prime} = r^{2}(1 -r^{2}) \label{8} \tag{8}$$

Para el caso de $\theta$ sustituimos (\ref{7}) en (\ref{6}).

$$r^{2} \theta^{\prime} = x[-y + x(1 -x^{2} -y^{2})] -y[x + y(1 -x^{2} -y^{2})]$$

Desarrollando, obtenemos

$$r^{2} \theta^{\prime} = r^{2} \label{9} \tag{9}$$

Por lo tanto, el sistema no lineal (\ref{7}) en coordenadas polares es el siguiente.

\begin{align*}
r^{\prime} &= r(1 -r^{2}) \\
\theta^{\prime} &= 1 \label{10} \tag{10}
\end{align*}

Este sistema esta desacoplado, de manera que podemos resolver cada ecuación por separado para obtener las funciones $r(t)$ y $\theta(t)$ explícitamente.

Comencemos con la ecuación de $r^{\prime}$. Dicha ecuación es separable.

\begin{align*}
\dfrac{dr}{dt} &= r(1 -r^{2}) \\
dr &= r(1 -r^{2}) dt \\
\int{\dfrac{dr}{r(1 -r^{2})}} &= \int{dt} \\
\end{align*}

Por un lado, tomando fracciones parciales, se tiene

\begin{align*}
\int{\dfrac{dr}{r(1 -r^{2})}} &= \int{ \left( \dfrac{1}{r} -\dfrac{1}{2(r + 1)} -\dfrac{1}{2(r -1)} \right) dr} \\
&= \int{\dfrac{dr}{r}} -\int{\dfrac{dr}{2(r + 1)}} -\int{\dfrac{dr}{2(r -1)}} \\
&= \ln|r|-\dfrac{1}{2} \ln|r + 1| -\dfrac{1}{2} \ln|r -1| + c_{1}\\
\end{align*}

y por otro lado,

$$\int{dt} = t + c_{2}$$

De ambos resultados se tiene que

$$\ln|r|-\dfrac{1}{2} \ln|r + 1| -\dfrac{1}{2} \ln|r -1| = t + c_{3}$$

Multipliquemos ambos lados de la igualdad por $-2$.

$$-2 \ln|r| + \ln|r + 1| + \ln|r -1| = -2t -2c_{3}$$

Ahora tomemos exponencial en ambos lados,

\begin{align*}
r^{-2}(r + 1)(r -1) &= e^{-2t -2c_{3}} \\
1 -r^{-2} &= e^{-2t} e^{-2c_{3}} \\
r^{-2} &= 1 -ce^{-2t}
\end{align*}

Por lo tanto,

$$r^{2} = \dfrac{1}{1 + ce^{-2t}} \label{11} \tag{11}$$

Como $r \geq 0$, entonces

$$r(t) = \dfrac{1}{\sqrt{1+ ce^{ -2t}}} \label{12} \tag{12}$$

Para el caso de la ecuación de $\theta^{\prime}$ es inmediato que

$$\theta(t) = t + t_{0} \label{13} \tag{13}$$

Por lo tanto, la solución general de (\ref{10}) es

\begin{align*}
r(t) &= \dfrac{1}{\sqrt{1+ ce^{ -2t}}} \\
\theta(t) &= t + t_{0} \label{14} \tag{14}
\end{align*}

De manera que la correspondiente solución del sistema no lineal (\ref{7}) es

\begin{align*}
x(t) &= \dfrac{\cos (t + t_{0})}{\sqrt{1 + ce^{ -2t}}} \\
y(t) &= \dfrac{\sin (t + t_{0})}{\sqrt{1+ ce^{ -2t}}} \label{15} \tag{15}
\end{align*}

Analizando el resultado (\ref{14}) se tienen 3 casos:

Si $c = 0$ se obtiene la solución

\begin{align*}
r(t) &= 1 \\
\theta(t) &= t + t_{0} \label{16} \tag{16}
\end{align*}

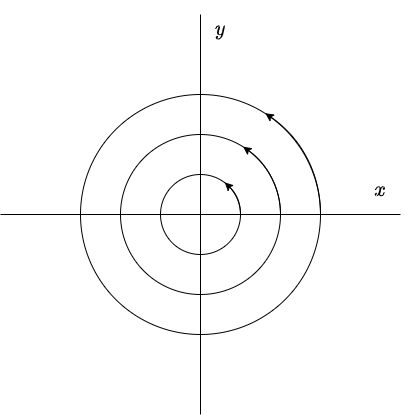
Que no es más que la circunferencia de radio $1$, $(x^{2} + y^{2} = 1)$ en sentido anti-horario.

Si $c < 0$ es claro que $r > 1$, $\theta = t + t_{0}$ y además,

$$ \lim_{t \to -\infty} \dfrac{1}{\sqrt{1+ ce^{ -2t}}} = \infty \hspace{1cm} y \hspace{1cm} \lim_{t \to \infty} \dfrac{1}{\sqrt{1+ ce^{ -2t}}} = 1 \label{17} \tag{17}$$

Finalmente, si $c > 0$ se observa que $r < 1$, $\theta = t + t_{0}$ y además,

$$\lim_{t \to -\infty} \dfrac{1}{\sqrt{1+ ce^{ -2t}}} = 0 \hspace{1cm} y \hspace{1cm} \lim_{t \to \infty} \dfrac{1}{\sqrt{1+ ce^{ -2t}}} = 1 \label{18} \tag{18}$$

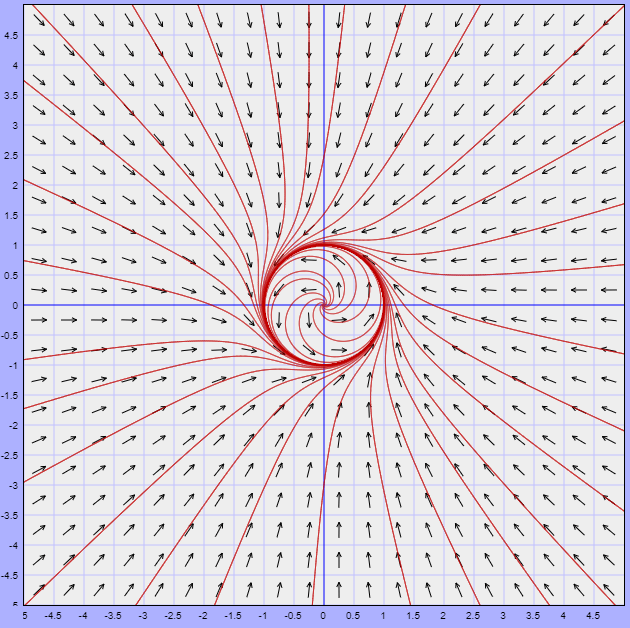
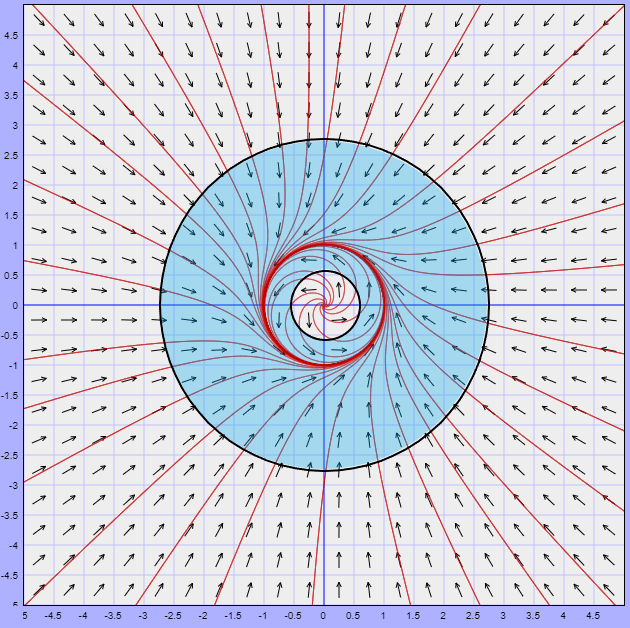
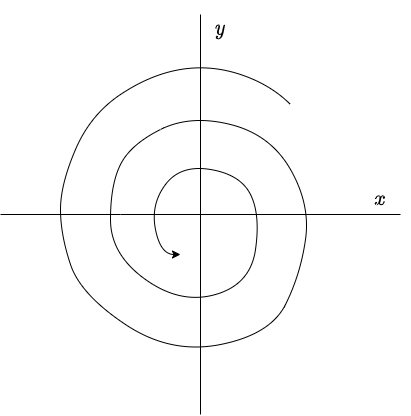
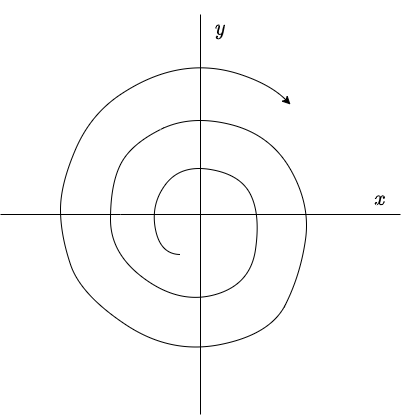
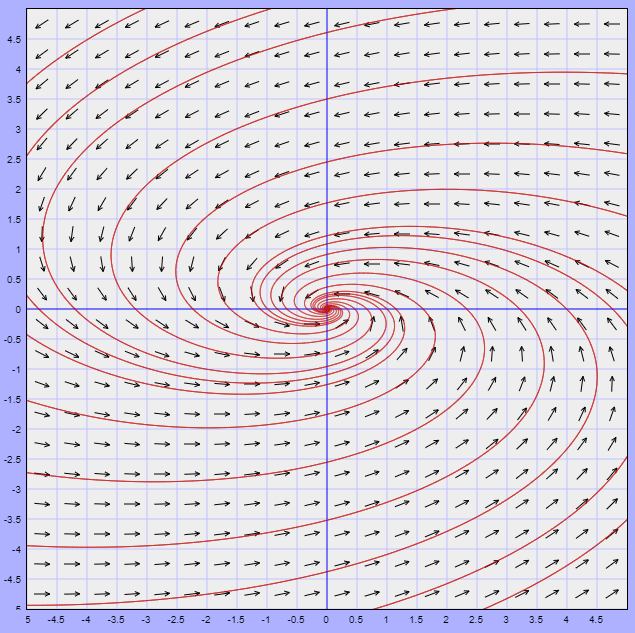
Lo que obtenemos es una curva cerrada o ciclo límite correspondiente a una trayectoria periódica para $r = 1$ y todas las demás trayectorias se acercan en espiral desde el exterior y el interior cuando $t \rightarrow \infty$, tal como se muestra en la siguiente figura.

Plano fase del sistema.

Nota: Este plano fase está definido con las trayectorias dadas por (\ref{15}), es decir, corresponde al plano $XY$.

Lo que hemos hecho es probar que el sistema no lineal (\ref{7}) tiene una trayectoria periódica, pero lo hemos hecho resolviendo el sistema explícitamente. Sin embargo, no siempre será sencillo resolver las ecuaciones involucradas, desearíamos de alguna manera saber si un sistema no lineal tiene o no trayectorias periódicas, pero sin conocer las soluciones explícitas. ¡Esto es posible con ayuda del teorema de Poincaré – Bendixson!.

Teorema de Poincaré – Bendixson en el plano.

Consideremos un sistema no lineal

\begin{align*}
x^{\prime} &= F_{1}(x, y) \\
y^{\prime} &= F_{2}(x, y) \label{19} \tag{19}
\end{align*}

La definición formal de ciclo límite es la siguiente.

En el ejemplo visto es claro que se trata de un ciclo límite estable.

En este caso, para que sean claras las siguientes definiciones, detonaremos a una solución del sistema (\ref{19}) como $Y(t; x, y)$ indicando que tanto $x$ como $y$ dependen de la variable $t$.

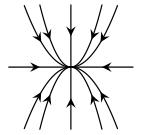
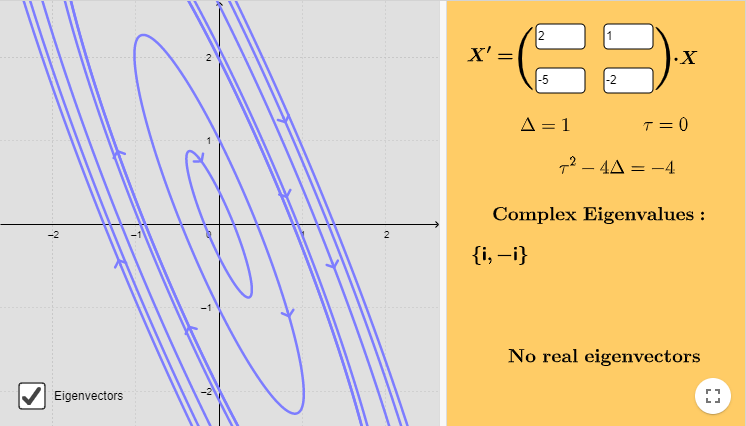
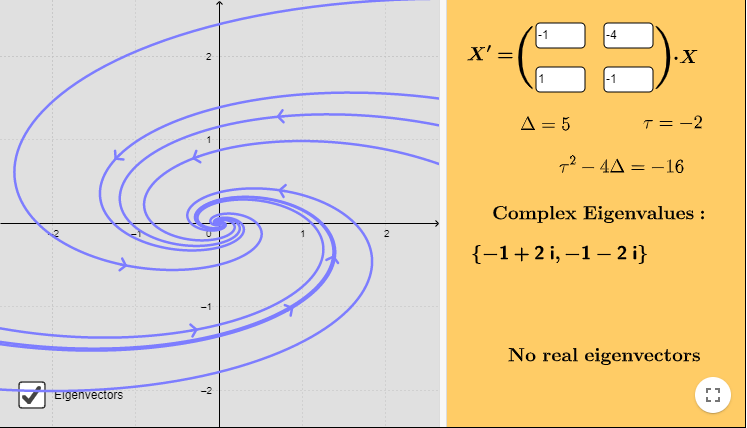
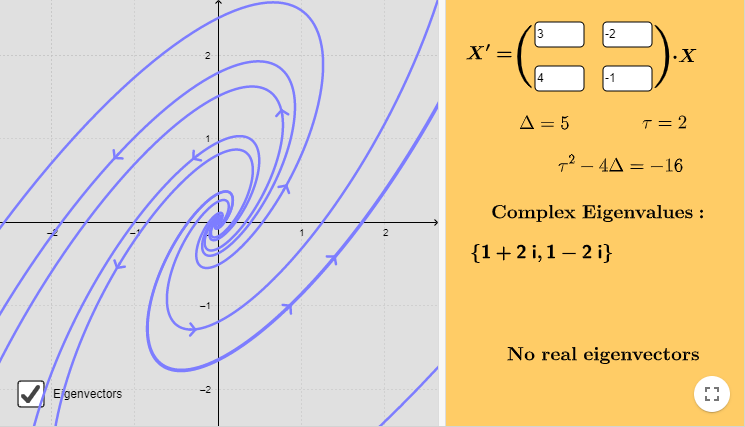
Ejemplo: Un sistema lineal cuyo punto de equilibrio es nodo atractor

Nodo atractor

tiene como punto $\omega -$límite al punto $Y_{0} = (0, 0)$, ya que cualquier trayectoria $Y(t_{n}; x, y)$ tiende a dicho punto para $t_{n} \rightarrow \infty$. Mas aún, el conjunto $\omega -$límite es $\omega(Y) = \{ (0, 0) \}$.

$\square$

Los conjuntos $\alpha -$límite y $\omega -$límite se pueden describir como el lugar geométrico donde nace y muere la trayectoria de la solución de un sistema dinámico dado.

En el primer ejemplo visto anteriormente obtuvimos una trayectoria periódica definida por la circunferencia $x^{2} + y^{2} = 1$, o bien $r = 1$. De acuerdo al plano fase, dicha circunferencia es un conjunto $\omega -$límite tanto para las trayectorias $Y(t; x, y)$ fuera de la circunferencia unitaria $(r > 0)$ como para las trayectorias $Y(t; x, y)$, dentro de la circunferencia unitaria $(r < 1)$.

Observando nuevamente el plano fase del sistema del ejemplo desarrollado, es posible encontrar un región por fuera de la circunferencia unitaria en la que las trayectorias se comiencen a trazar a partir de $t = 0$. Lo mismo se puede hacer en una región dentro de la circunferencia unitaria, de manera que dicha circunferencia quede completamente contenida en la unión de ambas regiones. Esto lo sabemos de los resultados (\ref{17}) y (\ref{18}).

Conjunto positivamente invariante.

Dicha unión de conjuntos corresponde al conjunto $U \subset \mathbb{R}^{2}$, en este caso, positivamente invariante ya que para todo punto $(x, y) \in U$ las trayectorias $Y(t; x, y) \in U$ para todo $t \geq 0$.

Ahora conocemos los conceptos básicos que nos permitirán comprender el teorema de Poincaré – Bendixson. Cabe mencionar que existen varias formas de enunciar este teorema dependiendo incluso de la profundidad teórica que se este tratando, sin embargo el resultado siempre será el mismo. Lo que haremos en este curso será enunciar el teorema de Poincaré-Bendixson de una forma un poco intuitiva, posteriormente lo enunciaremos nuevamente de forma formal y como corolarios de este teorema enunciaremos dos resultados importantes que incluso se pueden encontrar como enunciados del mismo teorema de Poincaré – Bendixson.

Comenzamos por enunciar el teorema de Poincaré – Bendixson de forma intuitiva.

Si recurrimos una vez más a nuestro ejemplo, podemos tomar la curva $\varphi_{1}$ como la frontera exterior del conjunto $U$, mientras que la curva $\varphi_{2}$ como la frontera interior del mismo conjunto.

Curvas que definen al conjunto positivamente invariante.

Lo que observamos es que el campo vectorial sobre los puntos de la curva $\varphi_{1}$ está dirigido hacia el interior de dicha curva, mientras que el campo vectorial sobre los puntos de la curva $\varphi_{2}$ está dirigido hacia el exterior. Es decir, en ambos casos el campo vectorial incide a la región positivamente invariante $U$ y sabemos que efectivamente hay una un ciclo límite comprendido entre ambas trayectorias.

Enunciemos ahora el teorema de Poincaré – Bendixson de manera más formal.

En esta entrada no demostraremos el teorema de Poincaré – Bendixson, sin embargo, en la sección de videos se ha hecho un enorme esfuerzo por desarrollar con detalle la teoría previa para su demostración, así como la demostración del teorema. Se recomienda visitar la entrada.

Antes de realizar algunos ejemplos enunciemos dos resultados importantes que se deducen del teorema de Poincaré – Bendixson.

Concluiremos esta entrada realizando algunos ejemplos en los que apliquemos el teorema de Poincaré – Bendixson, así como ambos corolarios para determinar que los sistemas no lineales estudiados presentan soluciones periódicas.

Ejemplo: Demostrar que el siguiente sistema no lineal tiene una trayectoria periódica.

\begin{align*}
x^{\prime} &= x -y -\left( x^{2} + \dfrac{3}{2}y^{2} \right)x \\
y^{\prime} &= x + y -\left( x^{2} + \dfrac{1}{2}y^{2} \right)y
\end{align*}

Solución: Por su puesto que intentar resolver el sistema para conocer explícitamente a la trayectoria periódica puede ser muy complicado, incluso si conociéramos métodos de resolución. Para poder aplicar el teorema de Poincaré – Bendixson lo que haremos será encontrar una región $U \subset \mathbb{R}^{2}$ que sea positivamente (o negativamente) invariante y que no contenga puntos de equilibrio del sistema.

Como ejercicio moral muestra que el único punto de equilibrio del sistema es el origen $Y_{0} = (0, 0)$. Esto nos indica que la región $U$ no debe contener al origen.

Nuevamente usemos coordenadas polares con la intención de hallar el intervalo en el que $r$ puede estar comprendido y cuyos valores extremos definan la región $U$ que buscamos.

Sustituyamos $x^{\prime}$ y $y^{\prime}$ del sistema no lineal en la ecuación (\ref{5}).

\begin{align*}
r r^{\prime} &= x \left[ x -y -\left( x^{2} + \dfrac{3}{2}y^{2} \right) x \right] + y \left[ x + y -\left( x^{2} + \dfrac{1}{2}y^{2} \right) y \right] \\
&= x^{2} + y^{2} -x^{4} -\dfrac{1}{2}y^{4} -\dfrac{5}{2}x^{2}y^{2} \\
&= (x^{2} + y^{2}) -(x^{4} +2x^{2}y^{2} + y^{4}) + \dfrac{1}{2}y^{4} -\dfrac{1}{2}x^{2}y^{2} \\
&= r^{2} -r^{4} + \dfrac{1}{2}y^{2}(y^{2} -x^{2})
\end{align*}

En el siguiente procedimiento haremos uso de las identidades trigonométricas

\begin{align*}
\cos(2 \theta) &= \cos^{2}(\theta) -\sin^{2}(\theta) \\
\cos(2 \theta) &= 1 -2\sin^{2}(\theta) \label{22} \tag{22}
\end{align*}

Si usamos las transformaciones (\ref{3}) y las identidades anteriores, tenemos lo siguiente.

\begin{align*}
y^{2}(y^{2} -x^{2}) &= r^{2} \sin^{2}(\theta) [r^{2} \sin^{2}(\theta) -r^{2} \cos^{2}(\theta)] \\
&= -r^{4} \sin^{2}(\theta) [\cos^{2}(\theta) -\sin^{2}(\theta)] \\
&= -r^{4} \sin^{2}(\theta) \cos(2 \theta) \\
&= -r^{4} \left[ \dfrac{1 -\cos(2 \theta)}{2} \right] \cos(2 \theta) \\
&= r^{4} \left[ \dfrac{\cos^{2}(2 \theta) -\cos(2 \theta)}{2} \right]
\end{align*}

Sustituyamos este resultado en nuestro desarrollo de $rr^{\prime}$.

$$rr^{\prime} = r^{2} -r^{4} + \dfrac{1}{2} r^{4} \left[ \dfrac{\cos^{2}(2 \theta) -\cos(2 \theta)}{2} \right]$$

De donde

$$r^{\prime} = r -r^{3} \left( 1+ \dfrac{\cos(2 \theta)}{4} -\dfrac{\cos^{2}(2 \theta)}{4} \right)$$

Para encontrar la región $U$ que contenga a la trayectoria periódica se debe hacer $r^{\prime} = 0$, debido a que tal región debe ser tangente a la trayectoria periódica en algún punto en el cual $r^{\prime} = 0$, entonces

$$r^{\prime} = r -r^{3} \left( 1+ \dfrac{\cos(2 \theta)}{4} -\dfrac{\cos^{2}(2 \theta)}{4} \right) = 0$$

Factorizando convenientemente se tiene,

$$\cos(2 \theta) -\cos^{2}(2 \theta) = 4 \left( \dfrac{1}{r^{2}} -1 \right)$$

Se puede hacer uso de un graficador para mostrar que

$$-2 \leq \cos(2 \theta) -\cos^{2}(2 \theta) < \dfrac{1}{4} \label{23} \tag{23}$$

Entonces se cumple la siguiente desigualdad

$$-2 \leq 4 \left ( \dfrac{1}{r^{2}} -1 \right ) < \dfrac{1}{4}$$

Desarrollando se tiene lo siguiente.

$$-\dfrac{1}{2} \leq \dfrac{1}{r^{2}} -1 < \dfrac{1}{16}$$

$$\dfrac{1}{2} \leq \dfrac{1}{r^{2}} < \dfrac{17}{16}$$

$$\dfrac{16}{17} \leq r^{2} < 2$$

Finalmente, el radio $r > 0$ tiene como desigualdades a

$$\dfrac{4}{\sqrt{17}} \leq r < \sqrt{2}$$

Observemos que si $r = \dfrac{4}{\sqrt{17}}$, entonces $r^{\prime} > 0$. En este caso, cualquier trayectoria por un punto en el conjunto

$$(x_{0}, y_{0}) \in \left\{ (x, y) \in \mathbb{R}^{2} : x^{2} + y^{2} < \left( \dfrac{4}{\sqrt{17}} \right)^{2} \right\}$$

sale del disco abierto

$$x^{2} + y^{2} < \left ( \dfrac{4}{\sqrt{17}} \right )^{2}$$

Por otro lado, si $r = \sqrt{2}$, entonces $r^{\prime} < 0$. En este caso, cualquier trayectoria por el punto

$$(x_{0}, y_{0}) \in \left\{ (x, y) \in \mathbb{R}^{2} : x^{2} + y^{2} > \sqrt{2} \right\}$$

entra al disco cerrado

$$x^{2} + y^{2} \leq \sqrt{2}$$

Por lo tanto, el conjunto

$$U = \left\{ (x, y) \in \mathbb{R}^{2} : \left( \dfrac{4}{\sqrt{17}} \right)^{2} \leq x^{2} + y^{2} \leq (\sqrt{2})^{2} \right\}$$

es un conjunto positivamente invariante. Esto quiere decir que para cualquier punto que se tome en el conjunto $U$, la trayectoria por este punto permanecerá en tal conjunto.

Como el punto de equilibrio $(0, 0)$ no pertenece a $U$, entonces por el teorema de Poincaré – Bendixson se concluye que existe una trayectoria periódica contenida en $U$.

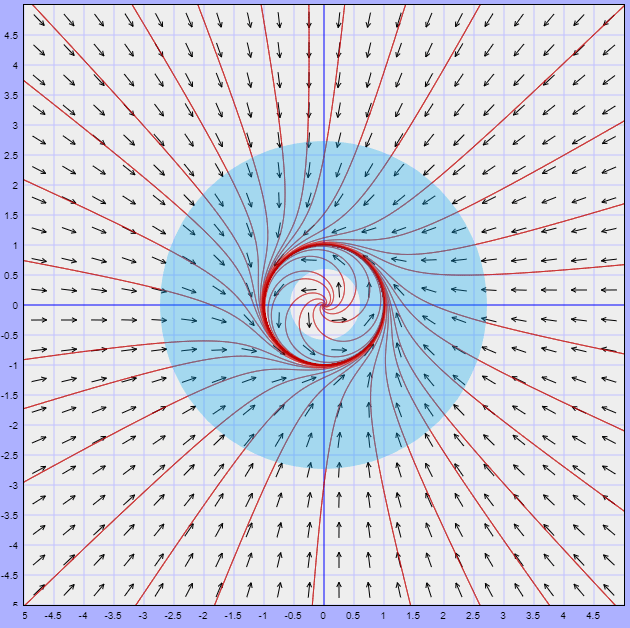
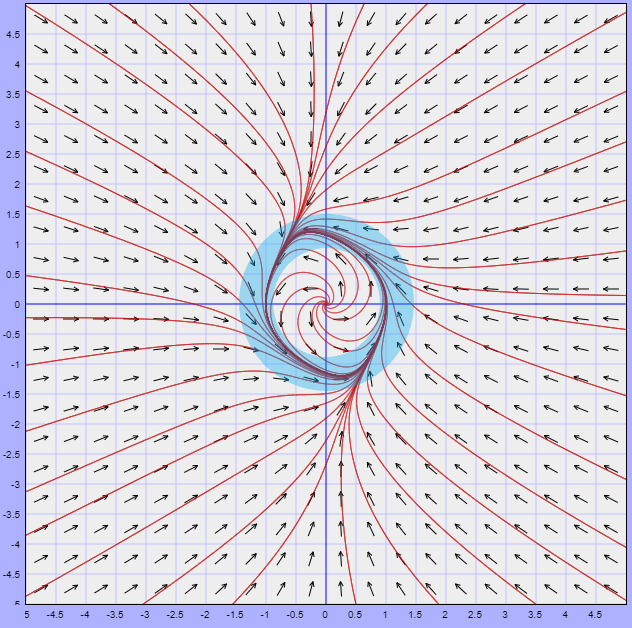
El plano fase del sistema no lineal, indicando la región $U$, se muestra a continuación.

Plano fase del sistema indicando la región positivamente invariante.

En la figura observamos que efectivamente la región $U$ contiene un conjunto límite correspondiente a una trayectoria periódica del sistema no lineal.

$\square$

Realicemos un ejemplo más.

Ejemplo: Mostrar que el siguiente sistema no lineal tiene por lo menos una trayectoria periódica.

\begin{align*}
x^{\prime} &= y \\
y^{\prime} &= -x + y(1 -x^{2} -2y^{2})
\end{align*}

Solución: El punto $Y_{0} = (0, 0)$ es el único punto de equilibrio del sistema. Debemos construir una región $U$ en la cual se pueda aplicar el Teorema de Poincaré – Bendixson.

Apliquemos la ecuación (\ref{5}).

\begin{align*}
rr^{\prime} &= x x^{\prime} + y y^{\prime} \\
&= x[y] + y[-x + y(1 -x^{2} -2y^{2})] \\
&= xy -xy + y^{2} -x^{2}y^{2} -2y^{4} \\
&= y^{2}(1 -x^{2} -2y^{2}) \\
&= r^{2} \sin^{2}(\theta) [1 -r^{2} \cos^{2}(\theta) -2r^{2} \sin^{2}(\theta)]
\end{align*}

De donde,

$$r^{\prime} = r \sin^{2}(\theta) [1 -r^{2} \cos^{2}(\theta) -2r^{2} \sin^{2}(\theta)]$$

Hacemos $r^{\prime} = 0$.

$$r \sin^{2}(\theta) [1 -r^{2} \cos^{2}(\theta) -2r^{2} \sin^{2}(\theta)] = 0$$

Como queremos hallar el intervalo que comprende a $r$ nos quedamos con la ecuación

$$1 -r^{2} \cos^{2}(\theta) -2r^{2} \sin^{2}(\theta) = 0$$

Desarrollando, se tiene

\begin{align*}
1 &= r^{2} \cos^{2}(\theta) + 2r^{2} \sin^{2}(\theta) \\
&= r^{2} [1 -\sin^{2}(\theta) + 2\sin^{2}(\theta) ]\\
&= r^{2} [1 + \sin^{2}(\theta)]
\end{align*}

De donde,

$$r^{2} = \dfrac{1}{1 + \sin^{2}(\theta)}$$

Sabemos que

$$0 \leq \sin^{2}(\theta) \leq 1$$

Entonces,

$$1 \leq 1 + \sin^{2}(\theta) \leq 2$$

$$\dfrac{1}{2} \leq \dfrac{1}{1 + \sin^{2}(\theta)} \leq 1$$

es decir,

$$\dfrac{1}{2} \leq r^{2} \leq 1$$

O bien,

$$\dfrac{1}{2} \leq x^{2} + y^{2} \leq 1$$

Esta desigualdad nos define la región $U$. Notemos que $r^{\prime} > 0$ para $x^{2} + y^{2} < \dfrac{1}{2}$. En este caso, cualquier trayectoria por el punto

$$(x_{0}, y_{0}) \in \left\{ (x, y) \in \mathbb{R}^{2} : x^{2} + y^{2} < \dfrac{1}{2} \right\}$$

sale del disco abierto

$$x^{2} + y^{2} < \dfrac{1}{2}$$

Por otro lado, $r^{\prime} \leq 0$ para $x^{2} + y^{2} > 1$. En este caso cualquier trayectoria por el punto

$$(x_{0}, y_{0}) \in \left\{ (x, y) \in \mathbb{R}^{2} : x^{2} + y^{2} > 1 \right\}$$

entra al disco cerrado

$$x^{2} + y^{2} \leq 1$$

Por lo tanto, el conjunto

$$U = \left\{ (x, y) \in \mathbb{R}^{2} : \dfrac{1}{2}< x^{2} + y^{2} < 1 \right\}$$

es positivamente invariante. Es decir, para cualquier punto que se tome en el conjunto $U$, la trayectoria por dicho punto permanecerá allí para $t \geq 0$. Como el origen no esta contenido en la región $U$, entonces es posible aplicar el Teorema de Poincaré – Bendixson mostrando así que existe al menos una órbita periódica en dicha región.

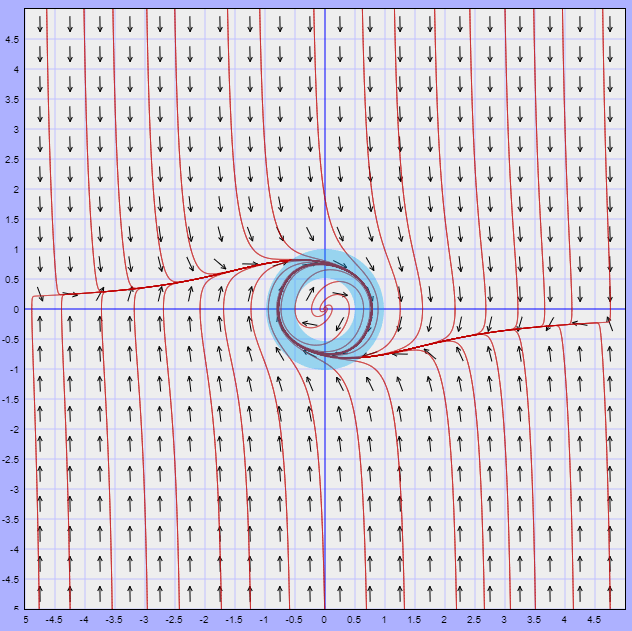
El plano fase del sistema, indicando la región $U$, es el siguiente.

Plano fase del sistema indicando la región positivamente invariante.

Efectivamente existe una trayectoria periódica contenida en la región $U$.

$\square$

Concluyamos con un último ejemplo.

Ejemplo: Mostrar que el siguiente sistema no lineal tiene por lo menos una trayectoria periódica.

\begin{align*}
x^{\prime} &= -y + x(r^{4} -3r^{2} + 1) \\
y^{\prime} &= x + y(r^{4} -3r^{2} + 1)
\end{align*}

con $r^{2} = x^{2} + y^{2}$.

Solución: El único punto de equilibrio del sistema es el origen $Y_{0} = (0, 0)$. Determinemos la región $U$ en la que podamos aplicar el teorema de Poincaré – Bendixson.

Sustituyamos las ecuaciones $x^{\prime}$ y $y^{\prime}$ del sistema en la ecuación (\ref{5}).

\begin{align*}
rr^{\prime} &= xx^{\prime} + yy^{\prime} \\
&= x[-y + x(r^{4} -3r^{2} + 1)] + y[ x + y(r^{4} -3r^{2} + 1)] \\
&= -xy + x^{2}(r^{4} -3r^{2} + 1) + xy + y^{2}(r^{4} -3r^{2} + 1) \\
&= (x^{2} + y^{2}) (r^{4} -3r^{2} + 1) \\
&= r^{2}(r^{4} -3r^{2} + 1)
\end{align*}

De donde,

$$r^{\prime} = r(r^{4} -3r^{2} + 1)$$

Si hacemos $r^{\prime} = 0$, obtenemos la ecuación de interés.

$$r^{4} -3r^{2} + 1 = 0$$

Hacemos $s = r^{2}$, de manera que la ecuación anterior se pueda escribir como

$$s^{2} -3s + 1 = 0$$

Las raíces de esta ecuación son

$$s_{1} = r^{2}_{1} = \dfrac{3 + \sqrt{5}}{2} \hspace{1cm} y \hspace{1cm} s_{2} = r^{2}_{2} = \dfrac{3 -\sqrt{5}}{2}$$

Si $r^{2} = \dfrac{3 + \sqrt{5}}{2}$ se verifica que $r^{\prime} > 0$ de forma que cualquier trayectoria por el punto

$$(x_{0}, y_{0}) \in \left \{ (x, y) \in \mathbb{R}^{2} : x^{2} + y^{2} < \dfrac{3 + \sqrt{5}}{2} \right \}$$

sale del disco cerrado

$$x^{2} + y^{2} \leq \dfrac{3 + \sqrt{5}}{2}$$

Si $r^{2} = \dfrac{3 -\sqrt{5}}{2}$ se verifica nuevamente que $r^{\prime} > 0$ de forma que cualquier trayectoria por el punto

$$(x_{0}, y_{0}) \in \left \{ (x, y) \in \mathbb{R}^{2} : x^{2} + y^{2} < \dfrac{3 -\sqrt{5}}{2} \right \}$$

sale del disco abierto

$$x^{2} + y^{2} < \dfrac{3 -\sqrt{5}}{2}$$

De ambos resultados notamos que el conjunto

$$U = \left \{ (x, y) \in \mathbb{R}^{2} : \dfrac{3 -\sqrt{5}}{2} \leq x^{2} + y^{2} \leq \dfrac{3 + \sqrt{5}}{2} \right \}$$

no es un conjunto ni positivamente ni negativamente invariante, pues en ambos casos las trayectorias salen de ambos discos.

Si tomamos $r = 1$ observamos que $r^{\prime} < 0$, es decir las trayectorias por un punto

$$(x_{0}, y_{0}) \in \left \{ (x, y) \in \mathbb{R}^{2} : x^{2} + y^{2} > 1 \right \}$$

entran al disco cerrado

$$x^{2} + y^{2} \leq 1$$

Este importante resultado nos indica que la región $U$ se puede dividir en dos regiones en las que una de ellas será positivamente invariante y la otra negativamente invariante, dichas regiones son.

$$U_{1} = \left \{ (x, y) \in \mathbb{R}^{2} : \dfrac{3 -\sqrt{5}}{2} \leq x^{2} + y^{2} \leq 1 \right \}$$

$$U_{2} = \left \{ (x, y) \in \mathbb{R}^{2} : 1 < x^{2} + y^{2} \leq \dfrac{3 + \sqrt{5}}{2} \right \}$$

Es claro que $U_{1}$ es un conjunto negativamente invariante y $U_{2}$ un conjunto positivamente invariante.

Como ninguna de ambas regiones contiene al punto de equilibrio, entonces podemos aplicar el teorema de Poincaré – Bendixson sobre cada una de las regiones deduciendo que en cada una de ellas existe una trayectoria periódica que corresponden a soluciones periódicas del sistema no lineal.

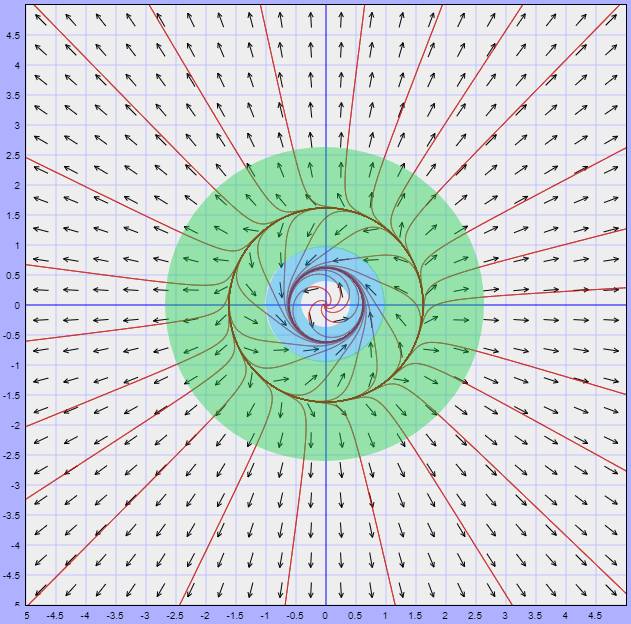
El plano fase del sistema, indicando ambas regiones, es el siguiente.

Plano fase del sistema indicando ambas regiones invariantes.

En este ejemplo mostramos que el sistema no lineal tiene dos trayectorias periódicas como solución.

$\square$

Felicidades, ¡Hemos concluido el curso!

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

  1. Mostrar que los siguientes sistemas no lineales tienen por lo menos un trayectoria periódica. Verifica tu resultado visualizando el plano fase del sistema.
  • $x^{\prime} = -y -\dfrac{x(x^{2} + y^{2} -2)}{\sqrt{x^{2} + y^{2}}}$
    $y^{\prime} = x -\dfrac{y(x^{2} + y^{2} -2)}{\sqrt{x^{2} + y^{2}}}$
  • $x^{\prime} = y + x(x^{2} + y^{2} -1)(x^{2} + y^{2} -2)$
    $y^{\prime} = -x + y(x^{2} + y^{2} -1)(x^{2} + y^{2} -2)$
  • $x^{\prime} = xy + x \cos (x^{2} + y^{2})$
    $y^{\prime} = -x^{2} + y \cos (x^{2} + y^{2})$

Más adelante…

Hemos concluido con el curso de Ecuaciones Diferenciales I.

Esperamos que este curso haya sido de tu agrado, lo hayas disfrutado y hayas aprendido mucho.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»

Ecuaciones Diferenciales I: Teoría cualitativa de los sistemas lineales homogéneos – Valores propios complejos

Por Omar González Franco

Deja un comentario

Las matemáticas es una ciencia que dibuja conclusiones necesarias.
– Benjamin Peirce

Introducción

En la entrada anterior estudiamos los sistemas lineales en los que los valores propios de la matriz $\mathbf{A}$ eran reales y distintos, en esta entrada estudiaremos sistemas lineales en los que los valores propios son complejos.

Antes de comenzar con el desarrollo cualitativo es conveniente recordar algunos resultados importantes de estos sistemas.

Sistemas lineales con valores propios complejos

El sistema que estamos analizando es

\begin{align*}
x^{\prime} &= ax + by \\
y^{\prime} &= cx + dy \label{1} \tag{1}
\end{align*}

Definimos,

$$\mathbf{Y}^{\prime} = \begin{pmatrix}
x^{\prime} \\ y^{\prime}
\end{pmatrix}, \hspace{1cm} \mathbf{Y} = \begin{pmatrix}
x \\ y
\end{pmatrix} \hspace{1cm} y \hspace{1cm} \mathbf{A} = \begin{pmatrix}
a & b \\ c & d
\end{pmatrix}$$

De manera que el sistema (\ref{1}) se pueda escribir como

$$\mathbf{Y}^{\prime} = \mathbf{AY} \label{2} \tag{2}$$

Sea

$$\lambda = \alpha + i \beta \label{3} \tag{3}$$

un valor propio de la matriz $\mathbf{A}$, con $\alpha$ y $\beta$ reales. Y sea

$$\mathbf{K} = \mathbf{U} + i \mathbf{V} \label{4} \tag{4}$$

un vector propio de $\mathbf{A}$ asociado a $\lambda$. Entonces la solución del sistema (\ref{1}) se puede escribir como

$$\mathbf{Y}(t) = (\mathbf{U} + i \mathbf{V}) e^{(\alpha + i \beta)t} \label{5} \tag{5}$$

En la unidad anterior vimos que si definimos los vectores

$$\mathbf{W}_{1} = Re \{ \mathbf{Y} \} \hspace{1cm} y \hspace{1cm} \mathbf{W}_{2} = Im \{ \mathbf{Y} \}$$

donde $\mathbf{W}_{1}$ y $\mathbf{W}_{2}$ están dados como

$$\mathbf{W}_{1}(t) = e^{\alpha t} [\mathbf{U} \cos(\beta t) -\mathbf{V} \sin(\beta t)] \label{6} \tag{6}$$

y

$$\mathbf{W}_{2}(t) = e^{\alpha t} [\mathbf{U} \sin(\beta t) + \mathbf{V} \cos(\beta t)] \label{7} \tag{7}$$

entonces la solución general real del sistema (\ref{1}) es

$$\mathbf{Y}(t) = c_{1} \mathbf{W}_{1}(t) + c_{2} \mathbf{W}_{2}(t) \label{8} \tag{8}$$

Por lo tanto, las soluciones linealmente independientes son

$$\mathbf{Y}_{1}(t) = c_{1} e^{\alpha t} \left[ \mathbf{U} \cos(\beta t) -\mathbf{V} \sin(\beta t) \right] \label{9} \tag{9}$$

y

$$\mathbf{Y}_{2}(t) = c_{2} e^{\alpha t} \left[ \mathbf{U} \sin(\beta t) + \mathbf{V} \cos(\beta t) \right] \label{10} \tag{10}$$

La expresión $k_{1} \cos(\beta t) + k_{2} \sin(\beta t)$, donde $k_{1}$ y $k_{2}$ son constantes, se puede expresar en la forma $R \cos(\beta t -\delta)$ para una elección adecuada de constantes $R$ y $\delta$. De tarea moral demuestra que la solución (\ref{8}) se puede expresar de la siguiente forma.

$$\mathbf{Y}(t) = e^{\alpha t} \begin{pmatrix}
R_{1} \cos(\beta t -\delta_{1}) \\ R_{2} \cos(\beta t -\delta_{2})
\end{pmatrix} \label{11} \tag{11}$$

para alguna elección de constantes $R_{1} \geq 0$, $R_{2} \geq 0$, $\delta_{1}$ y $\delta_{2}$.

Con esto en mente pasemos a estudiar cada caso en el que los valores propios son complejos.

Valores propios complejos con parte real nula

Caso 1: $\lambda_{1} = \alpha + i \beta$ y $\lambda_{2} = \alpha -i \beta$, con $\alpha = 0$.

En este caso se dice que los valores propios son imaginarios puros ya que no tienen parte real. De la solución (\ref{11}) vemos que si $\alpha = 0$, entonces la expresión se reduce a

$$\mathbf{Y}(t) = \begin{pmatrix}
R_{1} \cos(\beta t -\delta_{1}) \\ R_{2} \cos(\beta t -\delta_{2})
\end{pmatrix} \label{12} \tag{12}$$

Las soluciones $x(t)$ y $y(t)$ son

$$x(t) = R_{1} \cos(\beta t -\delta_{1}) \hspace{1cm} y \hspace{1cm} y(t) = R_{2} \cos(\beta t -\delta_{2}) \label{13} \tag{13}$$

Estas funciones son periódicas en el tiempo, con periodo $2 \pi / \beta$. Como $|\cos(\beta t -\delta_{1})| \leq 1$ y $|\cos(\beta t -\delta_{2})| \leq 1$, entonces la función $x(t)$ varia entre $-R_{1}$ y $+R_{1}$, mientras que $y(t)$ varia entre $-R_{2}$ y $+R_{2}$. Por tanto, la trayectoria de cualquier solución $\mathbf{Y}(t)$ de (\ref{1}) es una curva cerrada que rodea al origen $x = y = 0$, es por ello que se dice que el punto de equilibrio $Y_{0} = (0, 0)$ es un centro y es estable.

A continuación se muestra el plano fase.

Plano fase con parte real nula.

La dirección de las trayectorias se determina a partir del sistema (\ref{1}). Buscamos el signo de $y^{\prime}$ cuando $y = 0$. Si $y^{\prime}$ es mayor que cero para $y = 0$ y $x > 0$, entonces todas las trayectorias se mueven en sentido contrario a las manecillas del reloj. Si $y^{\prime}$ es menor que cero para $y = 0$ y $x > 0$, entonces todas las trayectorias se mueven en el sentido de las manecillas del reloj.

Ahora estudiemos los casos en los que los valores propios tienen parte real no nula.

Valores propios complejos con parte real negativa

Caso 2: $\lambda_{1} = \alpha + i \beta$ y $\lambda_{2} = \alpha -i \beta$, con $\alpha < 0$.

En este caso las soluciones son

$$\mathbf{Y}(t) = e^{\alpha t} \begin{pmatrix}
R_{1} \cos(\beta t -\delta_{1}) \\ R_{2} \cos(\beta t -\delta_{2})
\end{pmatrix}$$

o bien,

$$x(t) = e^{\alpha t} R_{1} \cos(\beta t -\delta_{1}) \hspace{1cm} y \hspace{1cm} y(t) = e^{\alpha t} R_{2} \cos(\beta t -\delta_{2}) \label{14} \tag{14}$$

Si $t = 0$, se obtiene que

$$\mathbf{Y}(0) = \begin{pmatrix}
R_{1} \cos(-\delta_{1}) \\ R_{2} \cos(-\delta_{2})
\end{pmatrix} \label{15} \tag{15}$$

Sabemos que el periodo es $2 \pi / \beta$, notemos que si $t = 2 \pi / \beta$, entonces

$$\mathbf{Y}(2 \pi / \beta) = e^{2 \pi \alpha / \beta} \begin{pmatrix}
R_{1} \cos(2 \pi -\delta_{1}) \\ R_{2} \cos(2 \pi -\delta_{2})
\end{pmatrix} = e^{2 \pi \alpha / \beta} \begin{pmatrix}
R_{1} \cos(-\delta_{1}) \\ R_{2} \cos(-\delta_{2})
\end{pmatrix}$$

esto es,

$$\mathbf{Y}(2 \pi / \beta) = e^{2 \pi \alpha / \beta } \mathbf{Y}(0) \label{16} \tag{16}$$

Como

$$\mathbf{Y}(2 \pi / \beta) < \mathbf{Y}(0)$$

es decir,

$$x(2 \pi / \beta) < x(0) \hspace{1cm} y \hspace{1cm} y( 2 \pi / \beta) < y(0)$$

entonces $\mathbf{Y}(2 \pi / \beta)$ está más cerca del origen que $\mathbf{Y}(0)$. Esto significa que, para $\alpha < 0$, el efecto del factor $e^{\alpha t}$ sobre la solución (\ref{11}) es el de cambiar las curvas cerradas del caso anterior en espirales que se aproximan hacia el origen.

El plano fase se muestra a continuación.

Plano fase con parte real negativa.

De forma similar al caso anterior, la dirección de las trayectorias se determina a partir del sistema (\ref{1}). En este caso se dice que el punto de equilibrio $Y_{0} = (0, 0)$ de (\ref{1}) es un foco estable, o también se conoce como espiral atractor. La estabilidad de este punto de equilibrio es asintóticamente estable.

Para concluir veamos que ocurre si $\alpha$ es positiva.

Valores propios complejos con parte real positiva

Caso 3: $\lambda_{1} = \alpha + i \beta$ y $\lambda_{2} = \alpha -i \beta$, con $\alpha > 0$.

En este caso nuevamente las soluciones son

$$\mathbf{Y}(t) = e^{\alpha t} \begin{pmatrix}
R_{1} \cos(\beta t -\delta_{1}) \\ R_{2} \cos(\beta t -\delta_{2})
\end{pmatrix}$$

o bien,

$$x(t) = e^{\alpha t} R_{1} \cos(\beta t -\delta_{1}) \hspace{1cm} y \hspace{1cm} y(t) = e^{\alpha t} R_{2} \cos(\beta t -\delta_{2})$$

Sin embargo, debido a que $\alpha > 0$, se puede probar que

$$\mathbf{Y}(2 \pi / \beta) > \mathbf{Y}(0)$$

es decir,

$$x(2 \pi / \beta) > x(0) \hspace{1cm} y \hspace{1cm} y( 2 \pi / \beta) > y(0)$$

lo que significa que ahora $\mathbf{Y}(0)$ está más cerca del origen que $\mathbf{Y}(2 \pi / \beta)$.

Por lo tanto, en este caso todas las soluciones de (\ref{1}) describen espirales que se alejan del origen conforme $t \rightarrow \infty$, y se dice que el punto de equilibrio $Y_{0} = (0, 0)$ de (\ref{1}) es un foco inestable o espiral repulsor. Es claro que el punto de equilibrio es inestable.

El plano fase se muestra a continuación.

Plano fase con parte real positiva.

Hemos revisado los casos posibles. Para concluir con la entrada realicemos un ejemplo por cada caso.

Caso 1: $\lambda_{1} = \alpha + i \beta$ y $\lambda_{2} = \alpha -i \beta$, con $\alpha = 0$.

Ejemplo: Resolver el siguiente sistema lineal y hacer un análisis cualitativo de las soluciones.

$$\mathbf{Y}^{\prime} = \begin{pmatrix}
2 & 1 \\ -5 & -2
\end{pmatrix} \mathbf{Y}$$

Solución: Determinemos los valores propios.

$$\begin{vmatrix}
2 -\lambda & 1 \\ -5 & -2 -\lambda
\end{vmatrix} = (2 -\lambda)(-2 -\lambda) + 5 = \lambda^{2} + 1 = 0$$

Las raíces son $\lambda_{1} = i$ y $\lambda_{2} = -i$, notamos que $\alpha = 0$ y $\beta = 1$, determinemos los vectores propios resolviendo la ecuación

$$(\mathbf{A} -i \mathbf{I}) \mathbf{K} = \mathbf{0}$$

o bien,

$$\begin{pmatrix}
2 -i & 1 \\ -5 & -2-i
\end{pmatrix} \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} = \begin{pmatrix}
0 \\ 0
\end{pmatrix}$$

Las ecuaciones que se obtienen son

\begin{align*}
(2 -i)k_{1} + k_{2} &= 0 \\
-5k_{1} -(2 + i)k_{2} &= 0
\end{align*}

Vemos que

$$k_{1} = -\left( \dfrac{2 + i}{5} \right)k_{2}$$

Sea $k_{2} = -5$, tal que $k_{1} = 2 + i$, así el primer vector propio es

$$\mathbf{K}_{1} = \begin{pmatrix}
2 + i \\ -5
\end{pmatrix} = \begin{pmatrix}
2 \\ -5
\end{pmatrix} + i \begin{pmatrix}
1 \\ 0
\end{pmatrix}$$

Sabemos que $\mathbf{K}_{2} = \bar{\mathbf{K}}_{1}$, entonces el segundo vector propio asociado al valor propio $\lambda_{2} = -i$ es

$$\mathbf{K}_{2} = \begin{pmatrix}
2 -i \\ -5
\end{pmatrix} = \begin{pmatrix}
2 \\ -5
\end{pmatrix} -i \begin{pmatrix}
1 \\ 0
\end{pmatrix}$$

La primera solución linealmente independiente es

$$\mathbf{Y}_{1}(t) = e^{it} \begin{pmatrix}
2 + i \\ -5
\end{pmatrix}$$

Notemos lo siguiente.

\begin{align*}
e^{it} \begin{pmatrix}
2 + i \\ -5
\end{pmatrix} &= \left[ \cos(t) + i \sin(t) \right] \left[ \begin{pmatrix}
2 \\ -5
\end{pmatrix} + i \begin{pmatrix}
1 \\ 0
\end{pmatrix} \right] \\
&= \cos(t) \begin{pmatrix}
2 \\ -5
\end{pmatrix} -\sin(t) \begin{pmatrix}
1 \\ 0
\end{pmatrix} + i \cos(t) \begin{pmatrix}
1 \\ 0
\end{pmatrix} + i \sin(t) \begin{pmatrix}
2 \\ -5
\end{pmatrix}
\end{align*}

De donde definimos

$$\mathbf{W}_{1} = \cos(t) \begin{pmatrix}
2 \\ -5
\end{pmatrix} -\sin(t) \begin{pmatrix}
1 \\ 0
\end{pmatrix}$$

y

$$\mathbf{W}_{2} = \sin(t) \begin{pmatrix}
2 \\ -5
\end{pmatrix} + \cos(t) \begin{pmatrix}
1 \\ 0
\end{pmatrix}$$

Por lo tanto, la solución general real es

$$\mathbf{Y}(t) = c_{1} \left[ \cos(t) \begin{pmatrix}
2 \\ -5
\end{pmatrix} -\sin(t) \begin{pmatrix}
1 \\ 0
\end{pmatrix} \right] + c_{2} \left[ \sin(t) \begin{pmatrix}
2 \\ -5
\end{pmatrix} + \cos(t) \begin{pmatrix}
1 \\ 0
\end{pmatrix} \right]$$

En términos de las funciones $x(t)$ y $y(t)$ se tienen las soluciones

\begin{align*}
x(t) &= [2c_{1} + c_{2}] \cos(t) + [-c_{1} + 2c_{2}] \sin(t) \\
y(t) &= -5c_{1} \cos(t) -5c_{2} \sin(t)
\end{align*}

Las soluciones son de la forma

\begin{align*}
x(t) &= k_{1} \cos(t) + k_{2} \sin(t) \\
y(t) &= k_{3} \cos(t) + k_{4} \sin(t)
\end{align*}

También es posible determinar las constantes $R_{1}$, $R_{2}$, $\delta_{1}$ y $\delta_{2}$ en términos de las constantes $c_{1}$ y $c_{2}$, tal que la solución se pueda escribir como

\begin{align*}
x(t) &= R_{1} \cos(t -\delta_{1})\\
y(t) &= R_{2} \cos(t -\delta_{2})
\end{align*}

En este caso como $\beta = 1$, entonces el periodo es $T = 2\pi$. La función paramétrica que define las trayectorias está dada por

$$f(t) = (k_{1} \cos(t) + k_{2} \sin(t), k_{3} \cos(t) + k_{4} \sin(t))$$

Es claro que las trayectorias son curvas cerradas con periodo $2 \pi$.

Para determinar la dirección de las trayectorias consideremos la ecuación $y^{\prime}$ del sistema, dicha ecuación es

$$y^{\prime} = -5x -2y$$

Si $y = 0$ se tiene la ecuación $y^{\prime} = -5x$, vemos que si $x > 0$, entonces $y^{\prime} < 0$, por lo tanto las trayectorias se mueven en el sentido de las manecillas del reloj.

El plano fase indicando algunas trayectorias se muestra a continuación.

Plano fase del sistema.

El campo vectorial está definido por la función

$$F(x, y) = (2x + y, -5x -2y)$$

A continuación se muestra dicho campo vectorial y algunas trayectorias.

Trayectorias y campo vectorial.

Efectivamente, el punto de equilibrio $Y_{0} = (0, 0)$ es un centro.

$\square$

Veamos como se pierde esta regularidad si $\alpha \neq 0$.

Caso 2: $\lambda_{1} = \alpha + i \beta$ y $\lambda_{2} = \alpha -i \beta$, con $\alpha < 0$.

Ejemplo: Resolver el siguiente sistema lineal y hacer un análisis cualitativo de las soluciones.

$$\mathbf{Y}^{\prime} = \begin{pmatrix}
-1 & -4 \\ 1 & -1
\end{pmatrix} \mathbf{Y}$$

Solución: Determinemos los valores propios.

$$\begin{vmatrix}
-1 -\lambda & -4 \\ 1 & -1 -\lambda
\end{vmatrix} = (-1 -\lambda)^{2} + 4 = \lambda^{2} + 2 \lambda + 5 = 0$$

Las raíces son $\lambda_{1} = -1 + 2i$ y $\lambda_{2} = -1 -2i$ (con $\alpha = -1$ y $\beta = 2$). Resolvamos la siguiente ecuación para obtener los vectores propios.

$$(\mathbf{A} -( -1 + 2i) \mathbf{I}) \mathbf{K} = \mathbf{0}$$

o bien,

$$\begin{pmatrix}
-2i & -4 \\ 1 & -2i
\end{pmatrix} \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} = \begin{pmatrix}
0 \\ 0
\end{pmatrix}$$

Se obtiene que $k_{1} = 2ik_{2}$. Sea $k_{2} = 1$, entonces $k_{1} = 2i$, así el primer vector propios es

$$\mathbf{K}_{1} = \begin{pmatrix}
2i \\ 1
\end{pmatrix} = \begin{pmatrix}
0 \\ 1
\end{pmatrix} + i \begin{pmatrix}
2 \\ 0
\end{pmatrix} $$

Considerando que $\mathbf{K}_{2} = \bar{\mathbf{K}}_{1}$ , entonces el segundo vector propio, asociado a $\lambda_{2} = -1 -2i$ es

$$\mathbf{K}_{2} = \begin{pmatrix}
-2i \\ 1
\end{pmatrix} = \begin{pmatrix}
0 \\ 1
\end{pmatrix} -i \begin{pmatrix}
2 \\ 0
\end{pmatrix}$$

Sabemos que la primer solución es

$$\mathbf{Y}_{1}(t) = e^{(-1 + 2i)t} \begin{pmatrix}
2i \\ 1
\end{pmatrix}$$

Notemos lo siguiente.

\begin{align*}
e^{(-1 + 2i)t} \begin{pmatrix}
2i \\ 1
\end{pmatrix} &= e^{-t} [\cos(2t) + i \sin(2t)] \left[ \begin{pmatrix}
0 \\ 1
\end{pmatrix} + i \begin{pmatrix}
2 \\ 0
\end{pmatrix} \right] \\
&= e^{-t} \left[ \cos(2t) \begin{pmatrix}
0 \\ 1
\end{pmatrix} -\sin(2t) \begin{pmatrix}
2 \\ 0
\end{pmatrix} + i \cos (2t) \begin{pmatrix}
2 \\ 0 \end{pmatrix} + i \sin(2t) \begin{pmatrix}
0 \\ 1 \end{pmatrix} \right]
\end{align*}

De donde definimos

$$\mathbf{W}_{1}(t) = e^{-t} \left[ \cos(2t) \begin{pmatrix}
0 \\ 1
\end{pmatrix} -\sin (t) \begin{pmatrix}
2 \\ 0
\end{pmatrix} \right]$$

y

$$\mathbf{W}_{2}(t) = e^{-t} \left[ \cos(t) \begin{pmatrix}
2 \\ 0
\end{pmatrix} + \sin(2t) \begin{pmatrix}
0 \\ 1
\end{pmatrix} \right]$$

Por lo tanto, la solución general real es

$$\mathbf{Y}(t) = c_{1} e^{-t} \left[ \cos(2t) \begin{pmatrix}
0 \\ 1
\end{pmatrix} -\sin (t) \begin{pmatrix}
2 \\ 0
\end{pmatrix} \right] + c_{2} e^{-t} \left[ \cos(t) \begin{pmatrix}
2 \\ 0
\end{pmatrix} + \sin(2t) \begin{pmatrix}
0 \\ 1
\end{pmatrix} \right]$$

Las funciones $x(t)$ y $y(t)$ son

\begin{align*}
x(t) &= -2c_{1}e^{-t} \sin(2t) + 2c_{2}e^{-t} \cos(2t) \\
y(t) &= c_{1}e^{-t} \cos(2t) + c_{2}e^{-t} \sin(2t)
\end{align*}

Estas funciones también se pueden escribir como

\begin{align*}
x(t) &= e^{-t} R_{1} \cos(2t -\delta_{1}) \\
y(t) &= e^{-t} R_{2} \cos(2t -\delta_{2})
\end{align*}

De tarea moral determina las constantes $R_{1}$, $R_{2}$, $\delta_{1}$ y $\delta_{2}$ en términos de las constantes $c_{1}$ y $c_{2}$.

Podemos notar que las soluciones ya no son trayectorias cerradas debido al término $e^{-t}$. En este caso el periodo es $t = 2 \pi / 2 = \pi$. Notemos que

\begin{align*}
x(0) &= 2c_{2} = R_{1} \cos(-\delta_{1}) \\
y(0) &= c_{1} = R_{2} \cos(-\delta_{2})
\end{align*}

Mientras que

\begin{align*}
x(\pi) &= 2 e^{-\pi} c_{2} = R_{1} e^{-\pi} \cos(-\delta_{1}) \\
y(\pi) &= e^{-\pi} c_{1} = R_{2} e^{-\pi} \cos(-\delta_{2})
\end{align*}

Como $e^{-\pi} < 1$, entonces

$$x(\pi) < x(0) \hspace{1cm} y \hspace{1cm} y(\pi) < y(0)$$

Por lo tanto las trayectorias corresponden a espirales que se aproximan hacia el origen.

La función paramétrica que define las trayectorias es

$$f(t) = (-2c_{1}e^{-t} \sin(2t) + 2c_{2}e^{-t} \cos(2t), c_{1}e^{-t} \cos(2t) + c_{2}e^{-t} \sin(2t))$$

Para determinar la dirección en que giran las trayectorias consideremos la ecuación $y^{\prime}$ del sistema, dicha ecuación es

$$y^{\prime} = x -y$$

Si $y = 0$, entonces $y^{\prime} = x$ y si $x > 0$, entonces $y^{\prime} > 0$, por lo tanto las trayectorias se mueven en el sentido opuesto a las manecillas del reloj.

El plano fase con algunas trayectorias se muestra a continuación.

Plano fase del sistema.

El campo vectorial asociado está definido por la función

$$F(x, y) = (-x -4y, x -y)$$

Dicho campo y algunas trayectorias se muestran en la siguiente figura.

Trayectorias y campo vectorial.

El punto de equilibrio $Y_{0} = (0, 0)$ es un foco estable.

$\square$

Concluyamos con un último ejemplo.

Caso 3: $\lambda_{1} = \alpha + i \beta$ y $\lambda_{2} = \alpha -i \beta$, con $\alpha > 0$.

Ejemplo: Resolver el siguiente sistema lineal y hacer un análisis cualitativo de las soluciones.

$$\mathbf{Y}^{\prime} = \begin{pmatrix}
3 & -2 \\ 4 & -1
\end{pmatrix} \mathbf{Y}$$

Solución: Determinemos los valores propios.

$$\begin{vmatrix}
3 -\lambda & -2 \\ 4 & -1 -\lambda
\end{vmatrix} = (3 -\lambda)(-1 -\lambda) + 8 = \lambda^{2} -2 \lambda + 5 = 0$$

Los valores propios son $\lambda_{1} = 1 + 2i$ y $\lambda_{2} = 1 -2i$ (con $\alpha = 1$ y $\beta = 2$ ). Determinemos los vectores propios con la ecuación

$$(\mathbf{A} -(1 + 2i) \mathbf{I}) \mathbf{K} = \mathbf{0}$$

o bien,

$$\begin{pmatrix}
2 -2i & -2 \\ 4 & -2 -2i
\end{pmatrix} \begin{pmatrix}
k_{1} \\ k_{2}
\end{pmatrix} = \begin{pmatrix}
0 \\ 0
\end{pmatrix}$$

De este sistema se obtiene que

$$k_{1} = \left( \dfrac{1+ i}{2} \right) k_{2}$$

Sea $k_{2} = 1$, entonces $k_{1} = \dfrac{1 + i}{2}$, así el primer vector propio es

$$\mathbf{K}_{1} = \begin{pmatrix}
\dfrac{1 + i}{2} \\ 1
\end{pmatrix} = \begin{pmatrix}
0 \\ 1
\end{pmatrix} + i \begin{pmatrix}
\dfrac{1}{2} \\ 0
\end{pmatrix} $$

y sabemos enseguida que

$$\mathbf{K}_{2} = \begin{pmatrix}
\dfrac{1 -i}{2} \\ 1
\end{pmatrix} = \begin{pmatrix}
0 \\ 1
\end{pmatrix} -i \begin{pmatrix}
\dfrac{1}{2} \\ 0
\end{pmatrix} $$

La primer solución linealmente independiente es

$$Y_{1}(t) = e^{(1 + 2i)t} \begin{pmatrix}
\dfrac{1 + i}{2} \\ 1
\end{pmatrix}$$

Vemos que

\begin{align*}
e^{(1 + 2i)t} \begin{pmatrix}
\dfrac{1 + i}{2} \\ 1
\end{pmatrix} &= e^{t} [\cos(2t) + i \sin(2t)] \left[ \begin{pmatrix}
\dfrac{1}{2} \\ 1
\end{pmatrix} + i \begin{pmatrix}
\dfrac{1}{2} \\ 0
\end{pmatrix} \right] \\
&= e^{t} \left[ \cos(2t) \begin{pmatrix}
\dfrac{1}{2} \\ 1
\end{pmatrix} -\sin(2t) \begin{pmatrix}
\dfrac{1}{2} \\ 0
\end{pmatrix} + i \cos(2t) \begin{pmatrix}
\dfrac{1}{2} \\ 0
\end{pmatrix} + i \sin(2t) \begin{pmatrix}
\dfrac{1}{2} \\ 1
\end{pmatrix} \right]
\end{align*}

de donde,

$$\mathbf{W}_{1}(t) = e^{t} \left[ \cos(2t) \begin{pmatrix}
\dfrac{1}{2} \\ 1
\end{pmatrix} -\sin(2t) \begin{pmatrix}
\dfrac{1}{2} \\ 0
\end{pmatrix} \right]$$

y

$$\mathbf{W}_{2}(t) = e^{t} \left[ \cos(2t) \begin{pmatrix}
\dfrac{1}{2} \\ 0
\end{pmatrix} + \sin(2t) \begin{pmatrix}
\dfrac{1}{2} \\ 1
\end{pmatrix} \right]$$

Por lo tanto, la solución general real del sistema es

$$\mathbf{Y}(t) = c_{1} e^{t} \left[ \cos(2t) \begin{pmatrix}
\dfrac{1}{2} \\ 1
\end{pmatrix} -\sin(2t) \begin{pmatrix}
\dfrac{1}{2} \\ 0
\end{pmatrix} \right] + c_{2} e^{t} \left[ \cos(2t) \begin{pmatrix}
\dfrac{1}{2} \\ 0
\end{pmatrix} + \sin(2t) \begin{pmatrix}
\dfrac{1}{2} \\ 1
\end{pmatrix} \right]$$

Las funciones $x(t)$ y $y(t)$ son

\begin{align*}
x(t) &= e^{t} \left( \dfrac{c_{1} + c_{2}}{2} \right) \cos(2t) + e^{t} \left( \dfrac{c_{2} -c_{1}}{2} \right) \sin(2t) \\
y(t) &= c_{1}e^{t} \cos(2t) + c_{2}e^{t} \sin(2t)
\end{align*}

El periodo de las soluciones es $T = 2 \pi / 2 = \pi$. Muestra, de manera similar a como lo hicimos en el ejemplo anterior, que

$$x(\pi) > x(0) \hspace{1cm} y \hspace{1cm} y(\pi) > y(0)$$

esto debido a que $e^{\pi} > 1$. Por lo tanto, las trayectorias describen espirales que se alejan del origen.

La función paramétrica que define a las trayectorias es

$$f(t) = (k_{1} e^{t} \cos(2t) + k_{2} e^{t} \sin(2t), c_{1}e^{t} \cos(2t) + c_{2}e^{t} \sin(2t) )$$

Con

$$k_{1} = \left( \dfrac{c_{1} + c_{2}}{2} \right) \hspace{1cm} y \hspace{1cm} k_{2} = \left( \dfrac{c_{2} -c_{1}}{2} \right)$$

Para determinar la dirección de las trayectorias consideremos la ecuación

$$y^{\prime} = 4x -y$$

Si $y = 0$ se obtiene que $y^{\prime} = 4x$ y si $x > 0$, entonces $y^{\prime} > 0$, por lo tanto, las trayectorias se mueven en el sentido opuesto a las manecillas del reloj.

El plano fase se muestra a continuación.

Plano fase del sistema.

La función vectorial que define al campo vectorial es

$$F(x, y) = (3x -2y, 4x -y)$$

El campo vectorial y algunas trayectorias se ilustran en la siguiente figura.

Trayectorias y campo vectorial.

El punto de equilibrio $Y_{0} = (0, 0)$ corresponde a un foco inestable.

$\square$

Hemos concluido con esta entrada. Continuemos en la siguiente entrada con el análisis en el caso en el que los valores propios de la matriz $\mathbf{A}$ son iguales.

Tarea moral

Los siguientes ejercicios no forman parte de la evaluación del curso, pero servirán para entender mucho mejor los conceptos vistos en esta entrada, así como temas posteriores.

  1. Resolver los siguientes sistemas lineales y hacer un análisis cualitativo de las soluciones.
  • $\mathbf{Y}^{\prime} = \begin{pmatrix}
    0 & 4 \\ -9 & 0
    \end{pmatrix} \mathbf{Y}$
  • $\mathbf{Y}^{\prime} = \begin{pmatrix}
    6 & -1 \\ 5 & 2
    \end{pmatrix} \mathbf{Y}$
  • $\mathbf{Y}^{\prime} = \begin{pmatrix}
    1 & -1 \\ 5 & -3
    \end{pmatrix} \mathbf{Y}$
  • $\mathbf{Y}^{\prime} = \begin{pmatrix}
    2 & -5 \\ 4 & -2
    \end{pmatrix} \mathbf{Y}$
  • $\mathbf{Y}^{\prime} = \begin{pmatrix}
    4 & 5 \\ -2 & 6
    \end{pmatrix} \mathbf{Y}$
  • $\mathbf{Y}^{\prime} = \begin{pmatrix}
    1 & -8 \\ 1 & -3
    \end{pmatrix} \mathbf{Y}$

Más adelante…

Continuando con nuestro estudio cualitativo de los sistemas lineales homogéneos con dos ecuaciones diferenciales, en la siguiente entrada veremos que ocurre en el plano fase cuando los valores propios de la matriz $\mathbf{A}$ son repetidos.

Entradas relacionadas

Agradecimientos

Trabajo realizado con el apoyo del Programa UNAM-DGAPA-PAPIME PE104522 «Hacia una modalidad a distancia de la Licenciatura en Matemáticas de la FC-UNAM – Etapa 2»