Introducción

Ahora que le hemos dado un orden a los elementos de un conjunto podemos decir más acerca de ellos. En esta sección hablaremos de aquellos elementos con características especiales, según sean éstas los llamaremos mínimos, máximos, minimales o maximales.

Mínimos y máximos

Comenzaremos definiendo a los mínimos y máximos en un conjunto parcialmente ordenado.

Definición: Sea $\leq$ un orden en $A$ y sea $B\subseteq A$. Decimos que $b\in B$ es elemento mínimo de $B$ en el orden $\leq$ si para cualquier $x\in B$, $b\leq x$. Denotamos al mínimo de $B$ como $\min(B)$.

Ejemplo:

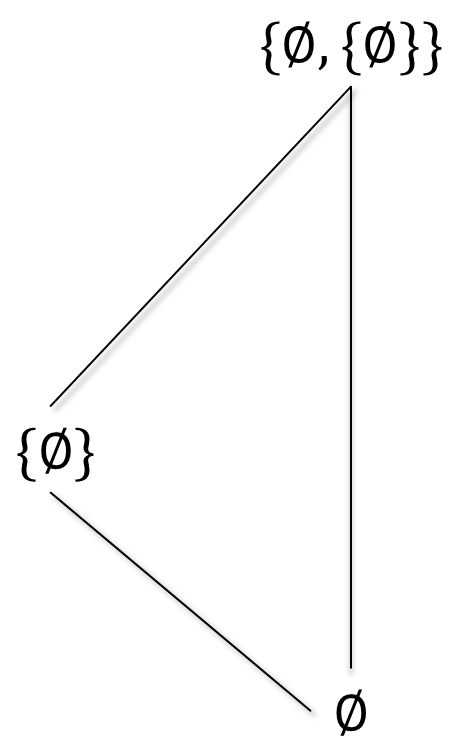
Consideremos $A= \set{\emptyset, \set{\emptyset}, \set{\emptyset, \set{\emptyset}}}$ y sea $\subseteq_A$ relación de orden en $A$. Si consideramos $A\subseteq A$, tenemos que $\emptyset$ es elemento mínimo pues para cada elemento de $A$, se tiene que $\emptyset$ esta por debajo o es igual a ellos. Más explícitamente, $\emptyset\subseteq \emptyset$, $\emptyset\subseteq \set{\emptyset}$ y $\emptyset\subseteq \set{\emptyset, \set{\emptyset}}$, como se muestra en el siguiente diagrama:

4$\square$

Definición: Sea $\leq$ un orden en $A$ y sea $B\subseteq A$. Decimos que $b\in B$ es elemento máximo de $B$ en el orden $\leq$ si para cualquier $x\in B$, $x\leq b$. Denotamos al máximo de $B$ como $\max(B)$.

Ejemplo:

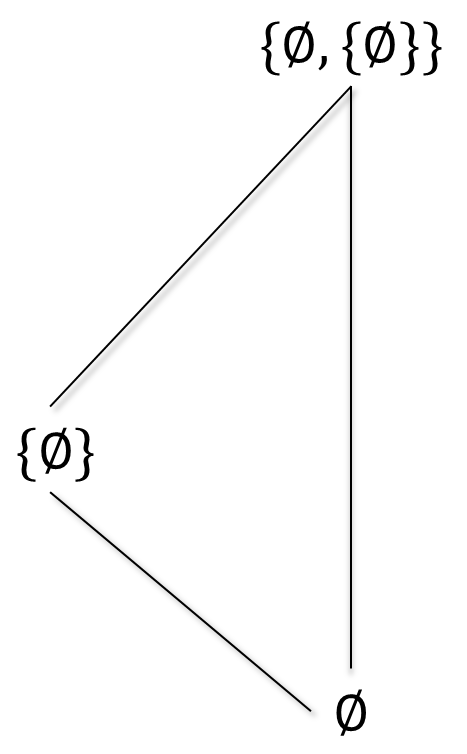
Consideremos $A= \set{\emptyset, \set{\emptyset}, \set{\emptyset, \set{\emptyset}}}$ y sea $\subseteq_A$ relación de orden en $A$. Si consideramos $A\subseteq A$, tenemos que $\set{\emptyset, \set{\emptyset}}$ es elemento máximo pues para cada elemento de $A$, se tiene que $\set{\emptyset, \set{\emptyset}}$ esta por encima o es igual a ellos. Más explícitamente, $\emptyset\leq \set{\emptyset, \set{\emptyset}}$, $\set{\emptyset}\leq \set{\emptyset, \set{\emptyset}}$ y $\set{\emptyset, \set{\emptyset}}\leq \set{\emptyset, \set{\emptyset}}$ como se muestra en el siguiente diagrama:

$\square$

Minimales y maximales

Definición: Sea $\leq$ un orden en $A$ y sea $B\subseteq A$. Decimos que $b\in B$ es elemento minimal de $B$ en el orden $\leq$ si no existe $x\in B$ tal que $x\leq b$ y $x\not=b$.

Ejemplo:

Consideremos $A= \set{\emptyset, \set{\emptyset}, \set{\emptyset, \set{\emptyset}}}$ y sea $\subseteq_A$ relación de orden en $A$. Si consideramos $A\subseteq A$, tenemos que $\emptyset$ es elemento minimal pues no existe $x\in B$ tal que $x\leq \emptyset$ y $x\not=\emptyset$.

$\square$

Definición: Sea $\leq$ un orden en $A$ y sea $B\subseteq A$. Decimos que $b\in B$ es elemento maximal de $B$ en el orden $\leq$ si no existe $x\in B$ tal que $b\leq x$ y $x\not=b$.

Ejemplo:

Consideremos $A=\set{\emptyset, \set{\emptyset}, \set{\emptyset, \set{\emptyset}}}$ y sea $\subseteq_A$ relación de orden en $A$. Si consideramos $A\subseteq A$, tenemos que $\set{\emptyset, \set{\emptyset}}$ es elemento maximal pues no existe $x\in B$ tal que $\set{\emptyset, \set{\emptyset}}\leq x$ y $x\not=\set{\emptyset, \set{\emptyset}}$.

$\square$

Diferencias

Podemos preguntarnos si la definición de minimal es equivalente a la de mínimo o si la de maximal es equivalente a la de máximo. Sin embargo, va a resultar que la definición de minimal y maximal son más débiles que la de mínimo y máximo, respectivamente. Veamos los siguientes ejemplos que muestran como a pesar de existir elementos minimales no existe el mínimo y como a pesar de existir elementos maximales no existe el máximo.

Ejemplo:

Consideremos $(\set{\set{\emptyset}, \set{\set{\emptyset}}, \set{\emptyset, \set{\emptyset}}}, \subseteq)$ un orden parcial. Veamos el siguiente diagrama:

En la imagen anterior podemos notar que $\set{\emptyset}\subseteq \set{\emptyset, \set{\emptyset}}$ y $\set{\set{\emptyset}}\subseteq \set{\emptyset, \set{\emptyset}}$ y que estás son las únicas relaciones posibles por la definición de contención. Luego, $\set{\emptyset}$ y $\set{\set{\emptyset}}$ son minimales pues no existe $x\in \set{\set{\emptyset}, \set{\set{\emptyset}}, \set{\emptyset, \set{\emptyset}}}$ tal que $x\leq \set{\emptyset}$ y $x\not=\set{\emptyset}$ ni $x\leq \set{\set{\emptyset}}$ y $x\not=\set{\set{\emptyset}}$.

Además, $\set{\set{\emptyset}, \set{\set{\emptyset}}, \set{\emptyset, \set{\emptyset}}}$ no tiene elemento mínimo pues de existir $x\in \set{\set{\emptyset}, \set{\set{\emptyset}}, \set{\emptyset, \set{\emptyset}}}$ tal que $x\leq y$ para todo $y\in \set{\set{\emptyset}, \set{\set{\emptyset}}, \set{\emptyset, \set{\emptyset}}}$, en particular, se tendría que $x\leq \set{\emptyset}$. Luego, el único elemento $x$ con esta propiedad en el conjunto $\set{\set{\emptyset},\set{\set{\emptyset}},\set{\emptyset,\set{\emptyset}}}$ es $\set{\emptyset}$ y en consecuencia, $x=\set{\emptyset}$. Por otro lado, por ser $x$ mínimo se tendría que $x\leq\set{\set{\emptyset}}$, y así $\set{\emptyset}\leq\set{\set{\emptyset}}$, es decir, $\set{\emptyset}\subseteq\set{\set{\emptyset}}$, lo cual no es verdad. Por lo tanto, no existe un mínimo en el conjunto $ \set{\set{\emptyset},\set{\set{\emptyset}},\set{\emptyset,\set{\emptyset}}} $.

$\square$

De este ejemplo podemos concluir que aunque un conjunto tenga minimal no necesariamente tendrá mínimo, esto se debe a que en un conjunto puede existir más de un elemento minimal y en cambio, si un conjunto tiene mínimo, entonces éste resulta ser único.

Ejemplo:

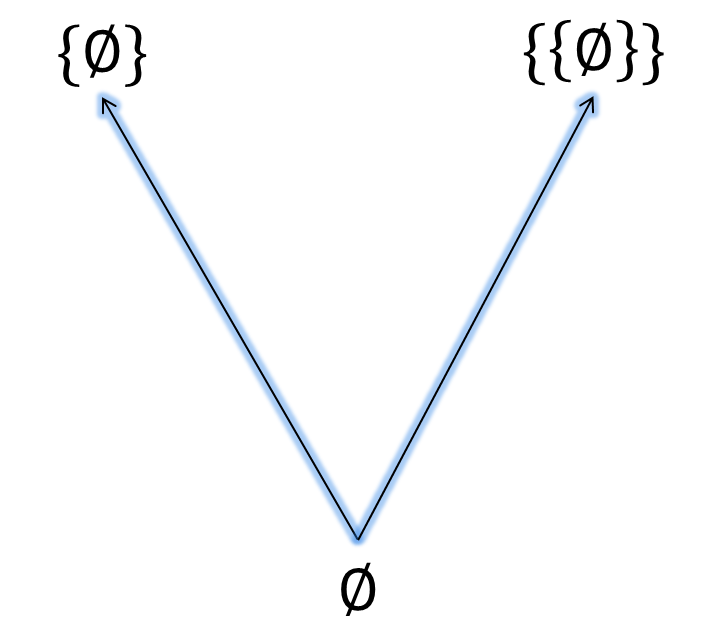
Consideremos $(\set{\emptyset, \set{\emptyset}, \set{\set{\emptyset}}}, \subseteq)$ un orden parcial. Veamos el siguiente diagrama:

En la imagen anterior podemos notar que $\emptyset\subseteq \set{\emptyset}$ y $\emptyset\subseteq \set{\set{\emptyset}}$ y que estás son las únicas relaciones posibles por la definición de contención. Luego, $\set{\emptyset}$ y $\set{\set{\emptyset}}$ son maximales pues no existe $x\in \set{\emptyset, \set{\emptyset}, \set{\set{\emptyset}}}$ tal que $\set{\emptyset}\leq x$ y $x\not=\set{\emptyset}$ y $\set{\set{\emptyset}}\leq x$ y $x\not=\set{\set{\emptyset}}$, respectivamente.

Notemos también que $\set{\emptyset, \set{\emptyset}, \set{\set{\emptyset}}}$ no tiene elemento máximo pues de existir $x\in \set{\emptyset, \set{\emptyset}, \set{\set{\emptyset}}} $ tal que $y\leq x$ para todo $y\in \set{\emptyset, \set{\emptyset}, \set{\set{\emptyset}}}$, se tendría en particular que $\set{\emptyset}\leq x$, de donde se sigue que $x=\set{\emptyset}$, pues este es el único elemento con tal propiedad en el conjunto $\set{\emptyset,\set{\emptyset},\set{\set{\emptyset}}}$. Luego, como $x=\set{\emptyset}$ es máximo se sigue que $\set{\set{\emptyset}}\leq\set{\emptyset}$, es decir, $\set{\set{\emptyset}}\subseteq\set{\emptyset}$, lo cual no es verdad. Por lo tanto, el conjunto $\set{\emptyset,\set{\emptyset},\set{\set{\emptyset}}}$ no tiene elemento máximo.

$\square$

De este ejemplo podemos concluir que aunque un conjunto tenga un elemento maximal no necesariamente tendrá máximo, esto se debe a que puede existir más de un elemento maximal y, si un conjunto tiene máximo, éste resulta ser único.

Definiciones para órdenes parciales estrictos

Definición: Sea $<$ un orden estricto en $A$ y sea $B\subseteq A$. Decimos que $b\in B$ es elemento mínimo de $B$ en el orden $<$ si para cualquier $x\in B\setminus\set{b}$, $b<x$. Denotamos al mínimo de $B$ como $\min(B)$.

Definición: Sea $<$ un orden estricto en $A$ y sea $B\subseteq A$. Decimos que $b\in B$ es elemento máximo de $B$ en el orden $<$ si para cualquier $x\in B\setminus\set{b}$, $x<b$. Denotamos al mínimo de $B$ como $\min(B)$.

Definición: Sea $<$ un orden estricto en $A$ y sea $B\subseteq A$. Decimos que $b\in B$ es elemento minimal de $B$ en el orden $<$ si no existe $x\in B$ tal que $x< b$.

Definición: Sea $<$ un orden en $A$ y sea $B\subseteq A$. Decimos que $b\in B$ es elemento maximal de $B$ en el orden $<$ si no existe $x\in B$ tal que $b< x$.

Tarea moral

La siguiente lista de ejercicios te permitirá reforzar el tema de esta sección:

• Si $(A, \leq)$ es un orden parcial y existe elemento mínimo en $A$, prueba que es único.
• Si $(A, \leq)$ es un orden parcial y existe elemento máximo en $A$, prueba que es único.
• Sea $(A, \leq)$ un orden parcial. Demuestra que si $A$ tiene máximo, entonces tiene maximal.
• Sea $(A, \leq)$ un orden parcial. Demuestra que si $A$ tiene mínimo, entonces tiene minimal.

Más adelante…

En la siguiente sección seguiremos hablando de elementos con características especiales en un conjunto según estén ordenados, esta vez hablaremos acerca de las cotas superiores e inferiores, así como de supremos e ínfimos.

Enlaces

• Entrada relacionada: Relación de pertenencia y relación de contención.
• Entrada anterior: Teoría de los Conjuntos I: Orden total
• Siguiente entrada: Teoría de los Conjuntos I: Cotas inferiores e ínfimos