Introducción
A lo largo de los teoremas vistos en geometría moderna se han demostrado y visto propiedades, pero gracias a la inversión se pueden deducir y demostrar nuevos teoremas de los ya vistos. A esto se le denomina Inversión de un Teorema.
Inversión de un Teorema y circunferencia de antisimilitud
Ejemplo. Dado un teorema referente a las alturas de un triángulo, se puede demostrar usando inversión y referente a circunferencias.
Sean $Z$ y $Z’$ dos circunferencias que se intersecan en $A$ y $O$, de $O$ se tiene los diámetros $OE$ de $Z’$ y $OF$ de $Z$ donde intersecan a $Z$ en $B$ y $Z’$ en $C$; Por lo cual el eje radical $AO$ pasa por el centro de la circunferencia de los puntos $O$, $B$ y $C$ la cual llamaremos $Z’$$’$.
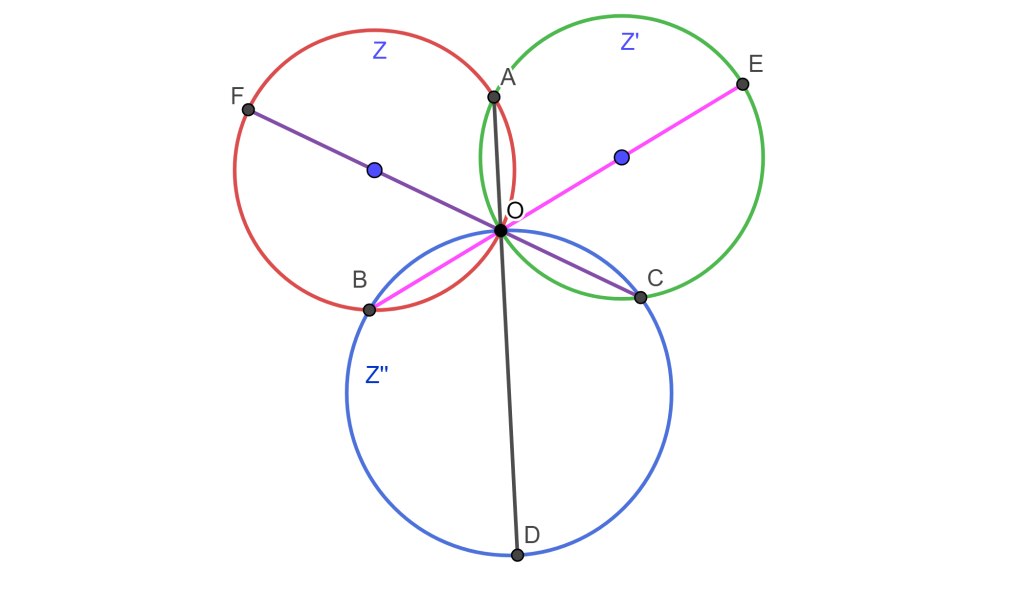
Usando el Teorema. El inverso de una circunferencia que pasa por el centro de inversión es una recta que no pasa por el centro de inversión: Por lo cual, usando $O$ como centro de inversión, se tiene que los inversos de $A$, $B$ y $C$ son $A’$, $B’$ y $C’$ respectivamente.
Las circunferencias $Z$, $Z’$ y $Z’$$’$ se invierten en $A’B’$, $A’C’$ y $B’C’$ correspondientemente. Y las líneas $AO$, $FO$ y $EO$ se invierten en sí mismas por Teorema de inversión de línea que pasa por el centro de inversión. Se tiene la inversión:
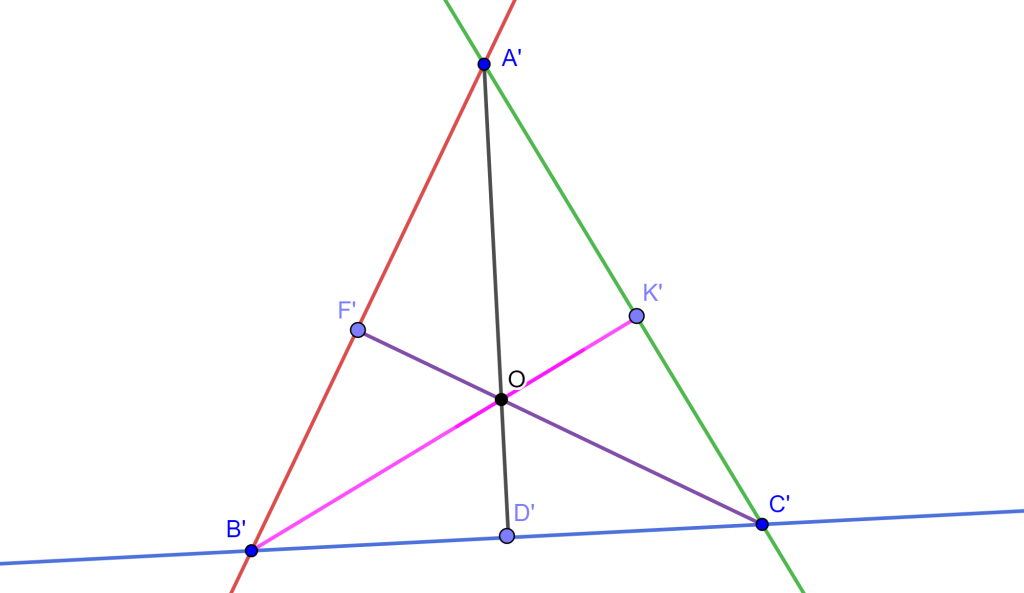
Ahora como un diámetro interseca su circunferencia ortogonalmente, entonces $B’O$ y $C’O$ por la propiedad de conservación de ángulos en la inversión son las alturas del triángulo $A’B’C’$, entonces $A’O \perp B’C’$.
Por lo tanto, $AO \perp $ $Z’$$’$ entonces $AO$ pasa por el centro de $Z’$$’.$
$\triangle$
Circunferencia de Antisimilitud
Definición. La circunferencia de antisimilitud es una circunferencia respecto a la cual dos circunferencias son mutuamente inversas.
Recordemos dos propiedades:
- El centro de inversión de dos circunferencias inversas es el centro de similitud.
- Dado un par de puntos inversos son antihomologos con respecto al centro de similitud.
Teorema. Sean dos circunferencias de las cuales existen tres posibles casos ($O$ y $O’$ centros de similitud).
Caso 1. Si se intersecan, entonces tienen dos circunferencias de antisimilitud tal que sus centros son los centros de similitud de las circunferencias dadas y que pasan por sus puntos de intersección.
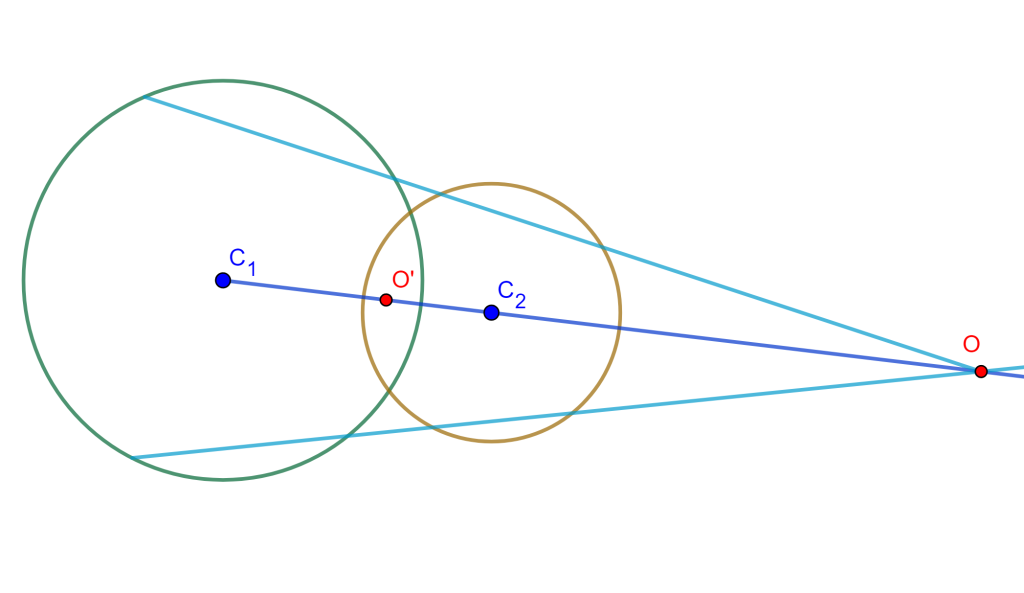
Caso 2. Si no se intersecan (o son tangentes), entonces solo tienen una circunferencia de antisimilitud cuyo centro está en el centro de similitud exterior si las circunferencias son mutuamente excluyentes.
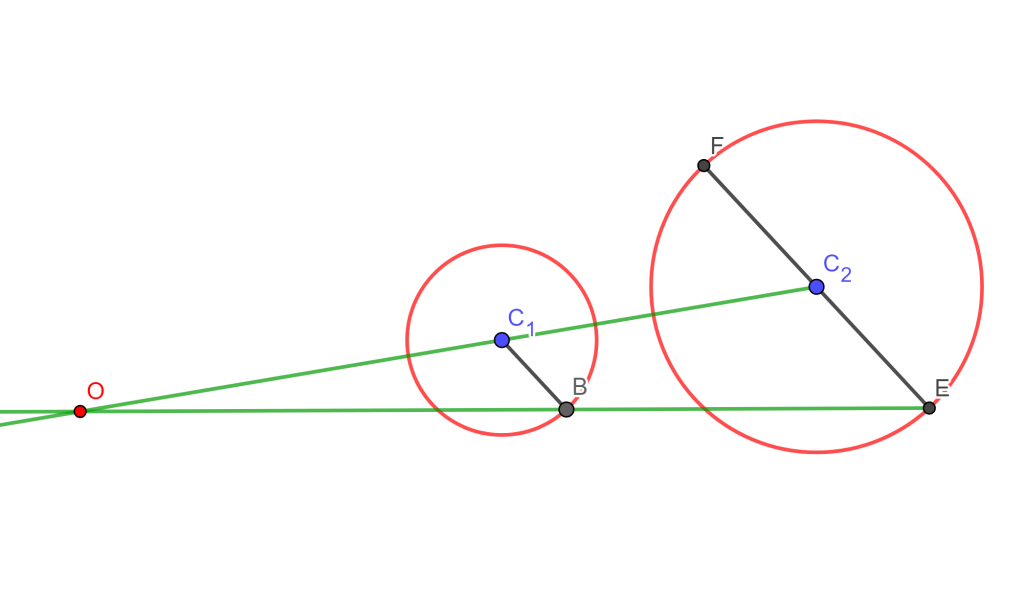
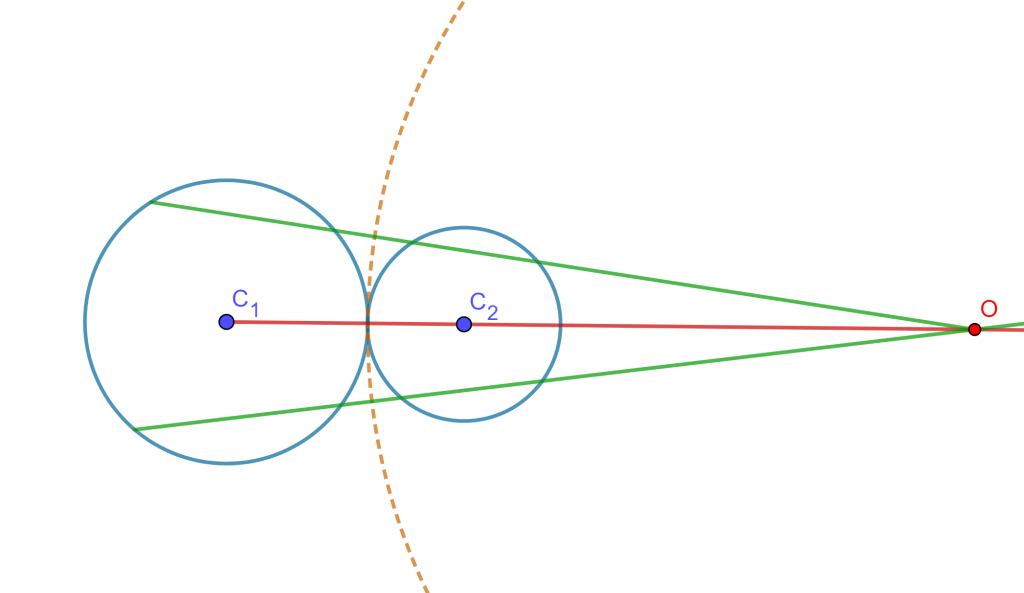
Caso 3. Si no se intersecan, entonces solo tiene una circunferencia de antisimilitud cuyo centro está en el centro de similitud interior si las circunferencias son internas una a la otra.
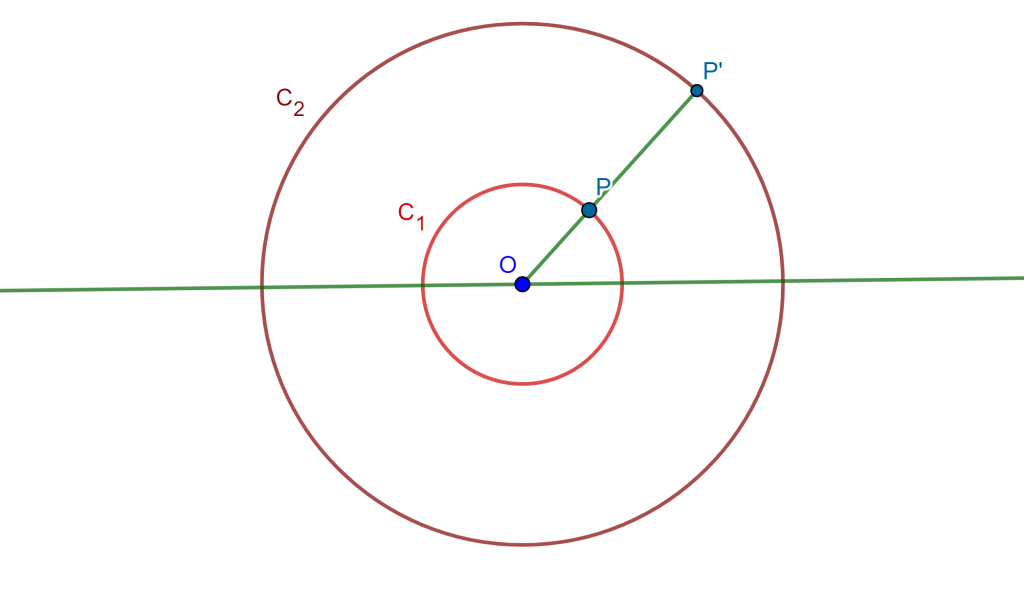
Lema. Una circunferencia $C_1$ y dos puntos inversos respecto a ella los llamaremos $S$ y $S’$ los cuales se invierten en una recta $C’_1$ y en dos puntos simétricos $P$ y $Q$ respecto a $C_1$, cuando el centro de inversión es un punto $A$ en $C_1$.
Teorema. Dos circunferencias que no se intersecan se pueden invertir en dos circunferencias iguales.
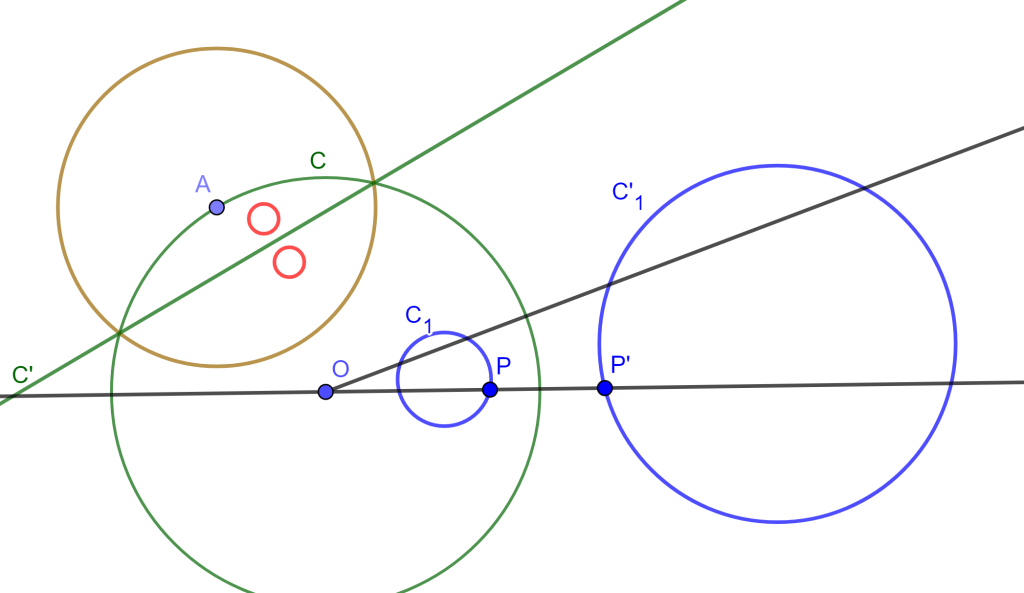
Demostración. Sean $C_1$ y $C’_1$ circunferencias y $C$ la circunferencia de antisimilitud de dichas circunferencias. Sea $A \in C$ y sea $C_2$ con centro $A$.
Las inversas de $C_1$ y $C’_1$ respecto a $C_2$ son dos circunferencias simétricas respecto al inverso de $C$ (Por el Lema anterior).
$\square$
Más adelante…
Es hora de ver algunas construcciones respecto a la inversión.
Entradas relacionadas
- Ir a Geometría Moderna II
- Entrada anterior del curso: Conservación de ángulos y razón cruzada
- Siguiente entrada del curso: Construcciones