Archivo de la etiqueta: ecuaciones de cauchy-riemann

Variable Compleja I: Ecuaciones de Cauchy-Riemann. Condiciones suficientes para la diferenciabilidad compleja.

Por Pedro Rivera Herrera

Deja un comentario

Introducción

En las entradas anteriores hemos definido y trabajado con los conceptos de diferenciabilidad y analicidad de una función compleja, en particular hemos visto que dichos conceptos no son equivalentes, desde que la analicidad de una función compleja en un punto $z_0$ implica la diferenciabilidad de la función en todo un $\varepsilon$-vecindario de $z_0$.

Como hemos visto a lo largo de la unidad 2, toda función compleja está totalmente definida a través de un par de funciones reales de dos variables, a las cuales hemos llamado su parte real e imaginaria. Más aún, hemos caracterizado algunos conceptos matemáticos importantes como el de límite y continuidad a través de dichas funciones, por lo que resulta natural cuestionarnos acerca de si es posible caracterizar la diferenciabilidad de una función compleja mediante estás funciones reales.

La entrada anterior deducimos las ecuaciones de Cauchy-Riemann y vimos que para una función compleja $f(z)=u(x,y) + iv(x,y)$ analítica en un conjunto abierto $U\subset\mathbb{C}$ las funciones $u$ y $v$, correspondientes con su parte real e imaginaria, deben satisfacer dichas ecuaciones. Sin embargo, vimos que dichas ecuaciones son solamente una condición necesaria, pero no suficiente, que las funciones $u$ y $v$ deben satisfacer. En esta entrada veremos que además de las ecuaciones de C-R, es necesario imponer unas condiciones extras sobre las funciones $u$ y $v$ para garantizar que una función compleja es analítica.

Recordemos la definición de diferenciabilidad de una función real de dos variables, vista en nuestros cursos de Cálculo.

Definición 18.1. (Diferenciabilidad de funciones reales de dos variables.)
Sea $U\subset\mathbb{R}^2$ un conjunto abierto. Una función real de dos variables $u:U \to \mathbb{R}$, es diferenciable en $(x_0,y_0) \in U$ si existen $A,B\in\mathbb{R}$ constantes tales que: \begin{equation*} \lim_{(x,y) \to (x_0, y_0)} \frac{u(x,y) – u(x_0, y_0) – A(x-x_0) – B(y-y_0)}{\sqrt{(x-x_0)^2 + (y-y_0)^2}} = 0, \end{equation*} en tal caso $A = \dfrac{\partial u}{\partial x}(x_0, y_0)$ y $B = \dfrac{\partial u}{\partial y}(x_0, y_0)$.

Observación 18.1.
De acuerdo con la definición 18.1, tenemos que una función real de dos variables $u$, definida sobre un abierto $U\subset \mathbb{R}^2$, es diferenciable en $(x_0,y_0)\in U$ si puede escribirse de la forma: \begin{equation*} u(x,y) = u(x_0,y_0) + A(x-x_0) + B(y-y_0) + \varepsilon(x,y)\sqrt{(x-x_0)^2 + (y-y_0)^2}, \end{equation*} donde $A = \dfrac{\partial u}{\partial x}(x_0, y_0)$ y $B = \dfrac{\partial u}{\partial y}(x_0, y_0)$ son constantes reales y $\lim\limits_{(x,y) \to (x_0,y_0)}\varepsilon(x,y) = 0$.

Consideremos el siguiente resultado.

Proposición 18.1.
Sean $U\subset\mathbb{C}$ un conjunto abierto y $f:U\to\mathbb{C}$ una función. Entonces, $f$ es analítica en $z_0\in U$ si y solo si $f$ se puede escribir de la forma: \begin{equation*} f(z) = f(z_0) + c(z-z_0) + \varepsilon(z)(z-z_0), \tag{18.2} \end{equation*} donde $c\in\mathbb{C}$ es una constante, $\varepsilon: U \to \mathbb{C}$ es continua en $z_0$ y $\lim\limits_{z \to z_0} \varepsilon(z) = 0$. En tal caso se tiene que $f'(z_0) = c$.

Demostración. Dadas las hipótesis, tenemos lo siguiente.

$\Rightarrow)$
Supongamos que $f'(z_0)$ existe, entonces definimos la función: \begin{equation*} \varepsilon(z)= \left\{ \begin{array}{lcc} \dfrac{f(z)- f(z_0)}{z – z_0} – f'(z_0) & \text{si} & z\neq z_0, \\ 0 & \text{si} & z = z_0. \end{array} \right. \end{equation*} Es claro que dicha función satisface que $\lim_{z \to z_0} \varepsilon(z) = 0$ y además es una función continua en $z_0$.

$(\Leftarrow$
Supongamos que $f(z)$ se puede escribir como (18.2) con $c\in\mathbb{C}$ constante, entonces para $z\neq z_0$, tenemos que: \begin{equation*} \frac{f(z) – f(z_0)}{z – z_0} = c + \varepsilon(z), \end{equation*} por lo que, tomando límites en la igualdad anterior: \begin{equation*} \lim_{z\to z_0} \frac{f(z) – f(z_0)}{z – z_0} = \lim_{z\to z_0} \left(c + \varepsilon(z)\right) = c, \end{equation*} de donde $f'(z_0) = c$.

$\blacksquare$

La proposición anterior establece que la diferenciabilidad de una función compleja $f(z)$ en $z_0$ es equivalente a que dicha función se puede aproximar en $z_0$ por la función lineal $f(z_0) + c(z-z_0)$, con $c\in\mathbb{C}$ constante, en el sentido que cuando $z$ está cerca de $z_0$ la diferencia entre $f(z)$ y $f(z_0) + c(z-z_0)$ es pequeña comparada con $|\,z-z_0\,|$.

Procedemos ahora a responder nuestra pregunta sobre cuáles son las condiciones suficientes que se deben imponer sobre las funciones $u$ y $v$, correspondientes con la parte real e imaginaria de una función compleja, además de las ecuaciones de C-R, para garantizar la analicidad de una función compleja.

Teorema 18.1.
Una función compleja $f(z) = u(x,y) + iv(x,y)$ es analítica en un conjunto abierto $U\subset\mathbb{C}$ si las cuatro derivadas parciales $u_x, v_x, u_y$ y $v_y$ existen y son continuas en todo punto de $U$ (es decir $u$ y $v$ son funciones de clase $C^1$) y satisfacen las ecuaciones de C-R en todo punto de $U$. En tal caso, para todo $z_0=x_0+iy_0\in U$ se tiene que: \begin{equation*} f'(z_0) = \frac{\partial u}{\partial x}(x_0,y_0) + i \frac{\partial v}{\partial x}(x_0,y_0) = \frac{\partial v}{\partial y}(x_0,y_0) – i \frac{\partial u}{\partial y}(x_0,y_0). \tag{18.3} \end{equation*}

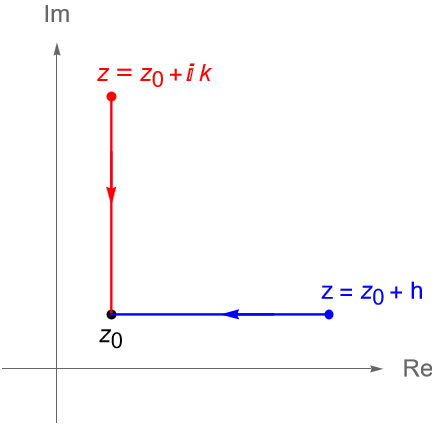
Demostración. Dadas las hipótesis, tomemos a $z_0 = x_0 + iy_0 \in U$ fijo, entonces existe $r>0$ tal que $B(z_0, r) \subset U$. Sea $z \in B(z_0, r)$ y supongamos que $z \neq z_0$, entonces tenemos que el segmento de recta que une a $z_0$ con $z$, es decir $[z_0, z]$, está totalmente contenido en $B(z_0, r)$ (¿por qué?). Sin perdida de generalidad supongamos que $x>x_0$ y $y>y_0$ (los casos restantes son completamente análogos), figura 74, por lo que: \begin{equation*} u(x,y) – u(x_0, y_0) = u(x,y) – u(x_0, y) + u(x_0, y) – u(x_0, y_0). \end{equation*}

Figura 74: Segmento de recta $[z_0, z]$ contenido en el disco abierto con centro en $z_0$ y radio $r>0$. Caso $x>x_0$ y $y>y_0$.

Definimos $h = x – x_0 > 0$ y $k = y – y_0 > 0$. Sean $g_1 : [0,h] \to \mathbb{R}$ y $g_2 : [0,k] \to \mathbb{R}$ dadas por: \begin{equation*} g_1(t) = u(x_0 + t,y) \quad \text{y} \quad g_2(t) = u(x_0,y_0 + t). \end{equation*}

Tenemos que: \begin{align*} g_1′(t) & = \lim_{h\to 0} \frac{g_1(t+h)-g_1(t)}{h}\\ & = \lim_{h\to 0} \frac{u(x_0 + t + h,y)-u(x_0 + t,y)}{h}\\ & = \frac{\partial u}{\partial x}(x_0 + t,y), \end{align*} \begin{align*} g_2′(t) & = \lim_{k\to 0} \frac{g_2(t+k)-g_2(t)}{k}\\ & = \lim_{k\to 0} \frac{u(x_0,y_0 + t + k)-u(x_0,y_0 + t)}{k}\\ & = \frac{\partial u}{\partial y}(x_0,y_0+t). \end{align*}

Como $u_x$ y $u_y$ existen en $U$, entonces para $y$ fijo tenemos que $g_1$ es una función diferenciable en $[0,h]$ y para $x_0$ fijo tenemos que $g_2$ también es una función diferenciable en $[0,k]$, por lo que $g_1$ y $g_2$ son funciones continuas en $[0,h]$ y $[0,k]$ respectivamente.

Por el teorema del valor medio para funciones reales, tenemos que existen $c_1\in(0,h)$ y $c_2\in(0,k)$ tales que: \begin{align*} g_1(h) – g_1(0) = g_1′(c_1) (h – 0),\\ g_2(h) – g_2(0) = g_2′(c_2) (k – 0), \end{align*} o equivalentemente que existen $\alpha_1, \beta_1 \in (0,1)$, tales que: \begin{align*} g_1(h) – g_1(0) = h \, g_1′(h\alpha_1),\\ g_2(h) – g_2(0) = k \, g_2′(k\beta_1), \end{align*} es decir: \begin{align*} u(x, y) – u(x_0, y) & = u(x_0 + h, y_0 + k) – u(x_0, y_0 + k)\\ & = h \, u_x(x_0 +\alpha_1 h, y_0 + k), \end{align*} \begin{align*} u(x_0, y) – u(x_0, y_0) & = u(x_0, y_0 + k) – u(x_0, y_0)\\ & = k \, u_y(x_0, y_0 + \beta_1 k). \end{align*} Por lo que: \begin{equation*} u(x,y) – u(x_0, y_0) = h \, u_x(x_0 +\alpha_1 h, y_0 + k) + k \, u_y(x_0, y_0 + \beta_1 k). \end{equation*}

De manera análoga concluimos que existen $\alpha_2, \beta_2 \in (0,1)$ tales que: \begin{align*} v(x_0 + h, y_0 + k) – v(x_0, y_0 + k) = h \, v_x(x_0 +\alpha_2 h, y_0 + k),\\ v(x_0, y_0 + k) – v(x_0, y_0) = k \, v_y(x_0, y_0 + \beta_2 k), \end{align*} donde $h = x – x_0 > 0$ y $k = y – y_0 > 0$.

Por lo que: \begin{equation*} v(x,y) – v(x_0, y_0) = h \, v_x(x_0 +\alpha_2 h, y_0 + k) + k \, v_y(x_0, y_0 + \beta_2 k). \end{equation*} Entonces, para $z\neq z_0$ tenemos que: \begin{align*} \frac{f(z) – f(z_0)}{z-z_0} & = \frac{u(x,y) + iv(x,y) – \left[ u(x_0,y_0) + iv(x_0,y_0)\right]}{(x – x_0) + i (y-y_0)}\\ & = \frac{u(x,y) – u(x_0,y_0)}{h + i k} + i \left[ \frac{v(x,y) – v(x_0,y_0)}{h + i k}\right]\\ & = \frac{h \, u_x(x_0 +\alpha_1 h, y_0 + k) + k \, u_y(x_0, y_0 + \beta_1 k)}{h + i k}\\ & \quad + i \left[ \frac{h \, v_x(x_0 +\alpha_2 h, y_0 + k) + k \, v_y(x_0, y_0 + \beta_2 k)}{h + i k}\right]\\ & = \frac{h}{h+ik}\left[u_x(x_0 +\alpha_1 h, y_0 + k) + i v_x(x_0 +\alpha_2 h, y_0 + k)\right]\\ & \quad + \frac{k}{h+ik} \left[u_y(x_0, y_0 + \beta_1 k) + i v_y(x_0, y_0 + \beta_2 k)\right], \end{align*} donde $h = x – x_0 > 0$, $k = y – y_0 > 0$ y $\alpha_i, \beta_i \in (0,1)$ para $i=1,2$. Además la igualdad anterior se cumple aún si $x = x_0$ o $y = y_0$.

Dado que $u_x, u_y, v_x$ y $v_y$ son continuas en $U$, entonces tenemos que: \begin{align*} \lim_{(h,k) \to (0,0)} u_x(x_0 +\alpha_1 h, y_0 + k) = u_x(x_0, y_0),\\ \lim_{(h,k) \to (0,0)} v_x(x_0 +\alpha_2 h, y_0 + k) = v_x(x_0, y_0),\\ \lim_{(h,k) \to (0,0)} u_y(x_0, y_0 + \beta_1 k) = u_y(x_0, y_0),\\ \lim_{(h,k) \to (0,0)} v_y(x_0, y_0 + \beta_2 k) = v_y(x_0, y_0). \end{align*} Por lo que: \begin{align*} \frac{f(z) – f(z_0)}{z-z_0} & = \frac{h}{h+ik}\left[u_x(x_0, y_0) + i v_x(x_0, y_0) + \varepsilon_1 \right]\\ & \quad + \frac{k}{h+ik} \left[u_y(x_0, y_0) + i v_y(x_0, y_0) + \varepsilon_2 \right], \end{align*} donde $\varepsilon_1, \varepsilon_2 \to 0$ si $(h,k) \to (0,0)$ o equivalentemente si $z \to z_0$.

Como se cumplen las ecuaciones de C-R, tenemos que: \begin{align*} u_x(x_0, y_0) = A = v_y(x_0, y_0),\\ u_y(x_0, y_0) = B = – v_x(x_0, y_0), \end{align*} para algunos $A$ y $B$ números reales.

Entonces: \begin{align*} \frac{f(z) – f(z_0)}{z-z_0} & = \frac{h}{h+ik}\left(A – i B\right) + \frac{k}{h+ik} \left(B + i A\right) + \frac{h \varepsilon_1 + k \varepsilon_2}{h+ik}\\ & = \frac{A\left(h + i k\right)}{h+ik} -i \frac{B\left(h + ik\right)}{h+ik} + \frac{h \varepsilon_1 + k \varepsilon_2}{h+ik}\\ & = A -iB + \frac{h \varepsilon_1 + k \varepsilon_2}{h+ik}\\ & = u_x(x_0, y_0) +iv_x(x_0,y_0) + \frac{h \varepsilon_1 + k \varepsilon_2}{h+ik}, \end{align*} donde $\varepsilon_1, \varepsilon_2 \to 0$ si $z \to z_0$.

Dado que para todo $z\in\mathbb{C}$ se cumple que $|\,\operatorname{Re}(z)\,| \leq |\,z\,|$ e $|\,\operatorname{Im}(z)\,| \leq |\,z\,|$, entonces: \begin{align*} 0<|\,h\,| \leq |\,h+ik\,| \quad \Longrightarrow \frac{|\,h\,|}{|\,h+ik\,|} \leq 1,\\ 0<|\,k\,| \leq |\,h+ik\,| \quad \Longrightarrow \frac{|\,k\,|}{|\,h+ik\,|} \leq 1. \end{align*} Por lo que: \begin{align*} \left| \, \frac{h \varepsilon_1 + k \varepsilon_2}{h+ik} \, \right| & \leq \left|\, \frac{h \varepsilon_1}{h+ik} \,\right| + \left|\, \frac{k \varepsilon_2}{h+ik} \,\right|\\ & = \frac{\left|\, h \,\right|}{\left|\, h+ik\,\right|} \left|\,\varepsilon_1 \,\right| + \frac{\left|\, k \,\right|}{\left|\,h+ik\,\right|} \left|\,\varepsilon_2 \,\right|\\ & \leq \left|\,\varepsilon_1 \,\right| + \left|\,\varepsilon_2 \,\right|, \end{align*} tomando límites en la desigualdad anterior concluimos que: \begin{equation*} \lim_{(h,k) \to (0,0)} \frac{h \varepsilon_1 + k \varepsilon_2}{h+ik} = \lim_{z \to z_0} \frac{(x-x_0) \varepsilon_1 + (y-y_0) \varepsilon_2}{(x-x_0)+i(y-y_0)} = 0. \end{equation*} Por tanto, tenemos que: \begin{align*} \lim_{z \to z_0} \frac{f(z) – f(z_0)}{z-z_0} & =\lim_{z \to z_0} \left( u_x(x_0, y_0) +iv_x(x_0,y_0) + \frac{(x-x_0) \varepsilon_1 + (y-y_0) \varepsilon_2}{(x-x_0)+i(y-y_0)} \right)\\ & =\lim_{z \to z_0} u_x(x_0, y_0) + \lim_{z \to z_0} iv_x(x_0,y_0) + \lim_{z \to z_0} \frac{(x-x_0) \varepsilon_1 + (y-y_0) \varepsilon_2}{(x-x_0)+i(y-y_0)}\\ & = u_x(x_0, y_0) +iv_x(x_0,y_0). \end{align*}

Entonces $f$ es analítica en $z_0 =x_0+iy_0 \in U$ y su derivada está dada por (18.3).

Dado que $z_0 = x_0 + iy_0\in U$ era arbitrario, entonces el resultado se cumple para todo punto en $U$.

$\blacksquare$

El resultado anterior es un primer recíproco parcial del teorema 17.1 de la entrada anterior, en el cual vimos que las ecuaciones de C-R son solo una condición necesaria, pero no suficiente, para la analicidad de una función compleja.

Observación 18.2.
Es importante recordar que los conceptos de diferenciabilidad y analicidad de una función no son intercambiables, por lo que puede suceder que una función sea diferenciable en un punto, pero no analítica en dicho punto. Considerando el resultado anterior podemos determinar a través de las ecuaciones de C-R dónde una función sí puede ser al menos diferenciable.

Ejemplo 18.1.
Sea $z=x+iy \in \mathbb{C}$. Consideremos a la función $f(z)=x^2+y^2+2ixy$. Veamos que $f$ no es analítica en ningún punto, pero es diferenciable en todo el eje real. Más aún, veamos que en dicho conjunto de puntos se tiene que $f'(z) = 2x$.

Solución. Considerando a la función $f$ tenemos que: \begin{equation*} u(x,y) = x^2 + y^2 \quad \quad \text{y} \quad \quad v(x,y) = 2xy. \end{equation*} Claramente ambas funciones están definidas sobre todo $\mathbb{C}$, por lo que $f$ está definida en $\mathbb{C}$.

Tenemos que: \begin{align*} \frac{\partial u}{\partial x} = 2x, \quad \frac{\partial u}{\partial y} = 2y,\\ \frac{\partial v}{\partial x} = 2y, \quad \frac{\partial v}{\partial y} = 2x. \end{align*} Es claro que las derivadas parciales existen y son continuas para todo $z = x+iy \in \mathbb{C}$.

Notemos que $u_x = v_y$, pero $u_y \neq -v_x$. Sin embargo: \begin{align*} \frac{\partial u}{\partial y} = – \frac{\partial v}{\partial x} \quad & \Longleftrightarrow \quad y = 0\\ & \Longleftrightarrow \quad z = \operatorname{Re}(z) = x. \end{align*}

Por lo que, por el teorema 18.1, concluimos que $f$ únicamente es diferenciable para todo $z$ en el eje real y su derivada en dicho conjunto de puntos es: \begin{equation*} f'(z) = f'(x) = \frac{\partial u}{\partial x}(x,0) + i \frac{\partial v}{\partial x}(x,0) = 2x. \end{equation*}

Dado que para todo $z_0=x_0+i0$ en el eje real y para todo $\delta>0$, existe $z_\delta=x_0 + i\frac{\delta}{2} \in B(z_0, \delta)$ un punto en donde $f$ no es diferenciable, entonces no existe un disco abierto alrededor de $z_0$ en el cual $f$ sea diferenciable y por tanto no es analítica en ningún punto sobre el eje real y en general en ningún punto en $\mathbb{C}$.

Ejemplo 18.2.
Sea $f:\mathbb{C} \to \mathbb{C}$ dada por $f(z)=x^2 – y^3 + i(x-y)$. Mostremos que $f$ no es analítica en $\mathbb{C}$ y determinemos el conjunto de puntos donde es diferenciable y hallemos su derivada en dicho conjunto.

Solución. De acuerdo con la definición de $f$ tenemos que: \begin{equation*} u(x,y) = x^2 – y^3 \quad \quad \text{y} \quad \quad v(x,y) = x-y. \end{equation*}

Tanto $u$ como $v$ son funciones reales diferenciables en todo punto en $\mathbb{R}^2$ y: \begin{align*} \frac{\partial u}{\partial x} = 2x, \quad \frac{\partial u}{\partial y} = -3y^2,\\ \frac{\partial v}{\partial x} = 1, \quad \frac{\partial v}{\partial y} = -1, \end{align*} las cuales existen y son continuas para todo punto en $\mathbb{R}^2$.

Es claro que $u_x \neq v_y$ y $u_y \neq -v_x$. Procedemos a determinar en qué puntos de $\mathbb{C}$ se satisfacen las igualdades: \begin{align*} \frac{\partial u}{\partial x} = \frac{\partial v}{\partial y} \quad & \Longleftrightarrow \quad 2x = -1\\ & \Longleftrightarrow \quad x = -\frac{1}{2}. \end{align*} \begin{align*} \frac{\partial u}{\partial y} = – \frac{\partial v}{\partial x} \quad & \Longleftrightarrow \quad -3y^2 = -1\\ & \Longleftrightarrow \quad y = \pm \frac{1}{\sqrt{3}}. \end{align*}

Sea $S = \left\{-\frac{1}{2}+i\frac{\sqrt{3}}{3}, -\frac{1}{2}-i\frac{\sqrt{3}}{3} \right\}$.

Entonces, por el teorema 18.1, concluimos que $f$ únicamente es diferenciable para $z_0 \in S$ y su derivada en dicho conjunto de puntos es: \begin{align*} f’\left(z_0\right) & = \frac{\partial u}{\partial x}\left(-\frac{1}{2},\pm \frac{\sqrt{3}}{3}\right) + i \frac{\partial v}{\partial x}\left(-\frac{1}{2},\pm \frac{\sqrt{3}}{3}\right)\\ & = -1 + i. \end{align*}

Notemos que para todo $z_0\in S$ y para todo $\delta>0$, existe $z_\delta=z_0 + \frac{\delta}{2} \in B(z_0, \delta)$ un punto en donde $f$ no es diferenciable, entonces no existe un disco abierto alrededor de $z_0$ en el cual $f$ sea diferenciable y por tanto no es analítica en ningún punto en $S$ y en general en ningún punto en $\mathbb{C}$.

Definición 18.2. (Dominio de analicidad.)
Un conjunto $U \subset \mathbb{C}$ es llamado un dominio de analicidad de una función compleja $f$ si $U$ es el mayor conjunto abierto en el cual $f$ es analítica.

Ejemplo 18.3
Para las funciones $f(z) = 1/z$ y $g(z) = \overline{z}$ tenemos que sus dominios de analicidad son los conjuntos $U = \mathbb{C} \setminus \{0\}$ y $G = \emptyset$ respectivamente.

Considerando la proposición 18.1 y la observación 18.1, planteamos el siguiente resultado en el cual establecemos cuales son las condiciones necesarias y suficientes que deben satisfacer las funciones reales $u$ y $v$, correspondientes con la parte real e imaginaria de una función compleja, para garantizar la analicidad de dicha función en un conjunto abierto $U\subset\mathbb{C}$.

Teorema 18.2.
Una función compleja $f(z) = u(x,y) + iv(x,y)$ es una función analítica en un conjunto abierto $U\subset\mathbb{C}$ si y solo si las funciones reales de dos variables $u$ y $v$ son diferenciables en $U$ y satisfacen las ecuaciones de C-R en todo punto de $U$. En tal caso, para todo $z_0=x_0+iy_0\in U$ se tiene que: \begin{equation*} f'(z_0) = \frac{\partial u}{\partial x}(x_0,y_0) + i \frac{\partial v}{\partial x}(x_0,y_0) = \frac{\partial v}{\partial y}(x_0,y_0) – i \frac{\partial u}{\partial y}(x_0,y_0). \tag{18.3.} \end{equation*}

Demostración. Sea $f(z) = u(x,y) + iv(x,y)$ una función compleja definida sobre un conjunto abierto $U\subset \mathbb{C}$ y sea $z = x+iy\in U$.

$\Rightarrow)$
Supongamos que $f$ es analítica en $U$ y sea $z_0 = x_0 +i y_0 \in U$ fijo. De acuerdo con la proposición 18.1, como la función $f$ es analítica en $z_0 \in U$, entonces puede escribirse como en (18.2), es decir de la forma: \begin{equation*} f(z) – f(z_0) = c(z-z_0) + \varepsilon(z)(z-z_0), \end{equation*} donde $c = f'(z_0) \in \mathbb{C}$ es constante y $\lim\limits_{z \to z_0} \varepsilon(z) = 0$.

Sea $c = f'(z_0) = A+iB\in\mathbb{C}$ para algunos $A$ y $B$ números reales. Entonces podemos reescribir esta última igualdad como: \begin{equation*} u(x,y) + iv(x,y) – \left[u(x_0,y_0) + iv(x_0,y_0)\right] = (A+iB)\left[(x-x_0) + i(y-y_0)\right] + \varepsilon(x+iy) \left[ (x-x_0) + i(y-y_0)\right]. \end{equation*} Separando en la parte real e imaginaria de la igualdad anterior obtenemos: \begin{align*} u(x,y) – u(x_0,y_0) = A(x-x_0) – B(y-y_0) + \operatorname{Re}\left( \varepsilon(x+iy) \left[ (x-x_0) + i(y-y_0)\right] \right),\\ v(x,y) – v(x_0,y_0) = B(x-x_0) + A(y-y_0) + \operatorname{Im}\left( \varepsilon(x+iy) \left[ (x-x_0) + i(y-y_0)\right] \right). \end{align*} Tenemos que: \begin{align*} \operatorname{Re}\left( \varepsilon(x+iy) \left[ (x-x_0) + i(y-y_0)\right] \right) & = \bigg(\operatorname{Re}\bigg[ \varepsilon(x+iy) \left[ (x-x_0) + i(y-y_0)\right] \bigg]\bigg) \frac{\sqrt{(x-x_0)^2 + (y-y_0)^2}}{\sqrt{(x-x_0)^2 + (y-y_0)^2}}\\ & = \bigg(\operatorname{Re}\bigg[\frac{\varepsilon(x+iy) \left[ (x-x_0) + i(y-y_0)\right]}{\sqrt{(x-x_0)^2 + (y-y_0)^2}} \bigg]\bigg) \sqrt{(x-x_0)^2 + (y-y_0)^2}\\ & =:\varepsilon_1(x,y) \sqrt{(x-x_0)^2 + (y-y_0)^2}, \end{align*} y de manera análoga obtenemos que: \begin{equation*} \operatorname{Im}\left( \varepsilon(x+iy) \left[ (x-x_0) + i(y-y_0)\right] \right) =: \varepsilon_2(x,y) \sqrt{(x-x_0)^2 + (y-y_0)^2}. \end{equation*} Por tanto: \begin{align*} u(x,y) – u(x_0,y_0) = A(x-x_0) – B(y-y_0) + \varepsilon_1(x,y) \sqrt{(x-x_0)^2 + (y-y_0)^2},\\ v(x,y) – v(x_0,y_0) = B(x-x_0) + A(y-y_0) + \varepsilon_2(x,y) \sqrt{(x-x_0)^2 + (y-y_0)^2}. \tag{18.4} \end{align*} Notemos que: \begin{equation*} |\, \varepsilon_1(x,y)\,| \leq |\, \varepsilon(z)\,| \quad \text{y} \quad |\, \varepsilon_2(x,y)\,| \leq |\, \varepsilon(z)\,|. \end{equation*} Dado que $\lim\limits_{z \to z_0} \varepsilon(z) = 0$, entonces tomando límites en estas dos desigualdades concluimos que: \begin{equation*} \lim_{(x,y) \to (x_0,y_0)} \varepsilon_1(x,y) = 0 \quad \text{y} \lim_{(x,y) \to (x_0,y_0)} \varepsilon_2(x,y) = 0. \tag{18.5} \end{equation*} Por lo tanto, considerando (18.4) y (18.5), se sigue de la observación 18.1 que $u$ y $v$ son funciones diferenciables en $(x_0,y_0)\in U$ y se cumple que: \begin{align*} \frac{\partial u}{ \partial x}(x_0,y_0) = A =\frac{\partial v}{ \partial y}(x_0,y_0),\\ \frac{\partial v}{ \partial x}(x_0,y_0) = B = -\frac{\partial u}{ \partial y}(x_0,y_0), \end{align*} es decir que se satisfacen las ecuaciones de C-R en $z_0 = x_0 + iy_0 \in U$. Dado que dicho punto era arbitrario entonces el resultado es válido para todo punto en $U$.

$(\Leftarrow$
Supongamos ahora que las funciones reales de dos variables $u$ y $v$ son diferenciables en un punto $(x_0, y_0) \in U$ y satisfacen las ecuaciones de C-R en dicho punto, entonces: \begin{align*} \frac{\partial u}{ \partial x}(x_0,y_0) = A =\frac{\partial v}{ \partial y}(x_0,y_0),\\ \frac{\partial v}{ \partial x}(x_0,y_0) = B = -\frac{\partial u}{ \partial y}(x_0,y_0) \end{align*} para algunos $A$ y $B$ números reales.

Por la observación 18.1 y considerando las igualdades anteriores tenemos que $u$ y $v$ se pueden escribir de la forma: \begin{align*} u(x,y) – u(x_0,y_0) = A(x-x_0) – B(y-y_0) + \varepsilon_1(x,y) \sqrt{(x-x_0)^2 + (y-y_0)^2},\\ v(x,y) – v(x_0,y_0) = B(x-x_0) + A(y-y_0) + \varepsilon_2(x,y) \sqrt{(x-x_0)^2 + (y-y_0)^2}, \end{align*} donde $\varepsilon_1(x,y) \to 0$ y $\varepsilon_2(x,y) \to 0$ si $(x,y) \to (x_0,y_0)$.

Considerando a la función $f(z) = u(x,y) + iv(x,y)$, tenemos que: \begin{align*} f(z) – f(z_0) & = u(x,y) + iv(x,y) – \left[u(x_0,y_0) + iv(x_0,y_0)\right]\\ & = u(x,y) – u(x_0,y_0) + i\left[ v(x,y) – v(x_0,y_0)\right]\\ & = A(x-x_0) – B(y-y_0) + \varepsilon_1(x,y) \sqrt{(x-x_0)^2 + (y-y_0)^2}\\ & \quad \quad + i \left[ B(x-x_0) + A(y-y_0) + \varepsilon_2(x,y) \sqrt{(x-x_0)^2 + (y-y_0)^2}\right]\\ & = (A+iB)\left[(x-x_0)+i(y-y_0)\right] + \sqrt{(x-x_0)^2 + (y-y_0)^2} \left[ \varepsilon_1(x,y) + i\varepsilon_2(x,y) \right]. \end{align*} Tomando: \begin{equation*} \varepsilon(x+iy) : = \frac{\sqrt{(x-x_0)^2 + (y-y_0)^2}}{(x-x_0) +i (y-y_0)}\left[ \varepsilon_1(x,y) + i\varepsilon_2(x,y) \right], \end{equation*} entonces: \begin{align*} f(z) – f(z_0) & = (A+iB)\left[(x-x_0)+i(y-y_0)\right] + \varepsilon(x+iy) \left[(x-x_0) +i (y-y_0)\right]\\ & = (A+iB)\left(z – z_0\right) + \varepsilon(z) \left( z- z_0\right). \tag{18.6} \end{align*} Claramente: \begin{equation*} |\, \varepsilon(z)\,| \leq |\, \varepsilon_1(x,y)\,| + |\, \varepsilon_2(x,y)\,|. \end{equation*} Como $\varepsilon_1(x,y) \to 0$ y $\varepsilon_2(x,y) \to 0$ si $(x,y) \to (x_0,y_0)$, entonces tomando límites en esta última desigualdad concluimos que: \begin{equation*} \lim\limits_{z \to z_0} \varepsilon(z) = 0. \tag{18.7} \end{equation*} Por lo tanto, considerando (18.6) y (18.7), se sigue de la proposición 18.1 que $f$ es analítica en $z_0 \in U$.

Más aún, tenemos que: \begin{equation*} f'(z_0) = A+iB = \frac{\partial u}{ \partial x}(x_0,y_0) + i \frac{\partial v}{ \partial x}(x_0,y_0) = \frac{\partial v}{ \partial y}(x_0,y_0) – i \frac{\partial u}{ \partial y}(x_0,y_0), \end{equation*} por lo que se cumple (18.3).

Dado que $z_0 = x_0 + iy_0\in U$ era arbitrario, entonces el resultado se cumple para todo punto en $U$.

$\blacksquare$

Observación 18.3.
Recordemos que hemos construido a $\mathbb{C}$ a través de $\mathbb{R}^2$, por lo que si pensamos a una función compleja $f$ como una función de $\mathbb{R}^2$ a $\mathbb{R}^2$ podemos preguntarnos acerca de la relación entre la diferenciabilidad compleja y la diferenciabilidad real de $f$.

Definición 18.3. (Diferenciabilidad de una función vectorial de dos variables.)
Sean $U\subset\mathbb{R}^2$ un conjunto abierto, $z_0 =(x_0,y_0) \in U$ y $f: U\to\mathbb{R}^2$ una función. Decimos que $f$ es diferenciable en $z_0$ (en el sentido real) si y solo si existe una transformación lineal $D_{f(z_0)} : \mathbb{R}^2 \to \mathbb{R}^2$ tal que: \begin{equation*}\lim_{z \to z_0}\frac{\|f(z)-f(z_0)-D_{f(z_0)}\left(z-z_0\right)\|}{\left\| z-z_0 \right\|} = 0, \tag{18.8} \end{equation*} donde $\|\cdot\|$ denota la norma usual en $\mathbb{R}^2$.

Por nuestros cursos de Cálculo sabemos que si una función vectorial de dos variables $f:U\to\mathbb{R}^2$, dada por $f(x,y) = (f_1(x,y),f_2(x,y))$, es diferenciable en un punto $z_0\in U\subset\mathbb{R}^2$, es decir existe el límite (18.8), entonces existen todas las derivadas parciales (de primer orden) en el punto $z_0$, de las funciones componentes de $f$ y al considerar la base canónica de $\mathbb{R}^2$, la matriz de $2\times2$ que representa a la transformación lineal $D_{f(z_0)}$ está formada por dichas derivadas parciales y recibe el nombre de la matriz Jacobiana, es decir: \begin{equation*} J_{f}(z_0) = \left(\begin{matrix} \frac{\partial f_1}{\partial x}(z_0) & \frac{\partial f_1}{\partial y}(z_0)\\ \\ \frac{\partial f_2}{\partial x}(z_0) & \frac{\partial f_2}{\partial y}(z_0) \end{matrix} \right). \tag{18.9} \end{equation*} Más aún, se prueba que $f$ es diferenciable en $U$ si y solo si $f_i: U \to \mathbb{R}$, con $i=1,2$, son funciones diferenciables en $U$.

De acuerdo con lo anterior podemos hacer algunas observaciones importantes. Notemos que la norma usal en $\mathbb{R}^2$ coincide con el módulo complejo en $\mathbb{C}$. Además, para una función compleja $f(z) = u(x,y) + iv(x,y)$, al considerarla como una función de $\mathbb{R}^2$ a $\mathbb{R}^2$, se tiene que las funciones componentes de $f$ son: \begin{equation*} f_1(x,y) = u(x,y), \quad f_2(x,y) = v(x,y). \tag{18.10} \end{equation*}

Considerando a un número complejo $\lambda = a+ib$ fijo y $z=x+iy\in\mathbb{C}$, tenemos que su producto es: \begin{equation*} \lambda z = (a+ib)(x+iy) = (ax -by) + i(ay + bx). \end{equation*}

Por lo que, a través del producto de dos números complejos es posible definir una trasnformación lineal de $\mathbb{R}^2$ a $\mathbb{R}^2$, como sigue. Sean $\lambda=(a,b)\in\mathbb{R}^2$ constante y $z=(x,y)\in\mathbb{R}^2$, entonces: \begin{equation*} M_{\lambda} : \mathbb{R}^2 \to \mathbb{R}^2, \quad M_{\lambda}(z) = \begin{pmatrix} ax-by\\ ay+bx \end{pmatrix} = \begin{pmatrix} a & -b\\ b & a \end{pmatrix} \begin{pmatrix} x\\ y \end{pmatrix}, \tag{18.11} \end{equation*} de donde es claro que la matriz $A = \begin{pmatrix} a & -b\\ b & a \end{pmatrix}$ representa, en la base canónica de $\mathbb{R}^2$, a la transformación $M_\lambda$ correspondiente con la multiplicación de dos números complejos.

Procedamos ahora a analizar la definición de diferenciabilidad compleja dada en la entrada 16. De acuerdo con la definición 16.1, sabemos que para $U\subset\mathbb{C}$ un conjunto abierto y $f:U \to \mathbb{C}$ una función, decimos que $f$ es diferenciable en $z_0\in U$ si existe el límite: \begin{equation*} \lim_{z\to z_0} \frac{f(z) – f(z_0)}{z-z_0}, \end{equation*} lo cual es equivalente a que exista un número complejo $\lambda = a+ib\in\mathbb{C}$ tal que: \begin{align*} \lim_{z\to z_0} \frac{f(z) – f(z_0)}{z-z_0} = \lambda \quad & \Longleftrightarrow \quad \lim_{z\to z_0} \frac{f(z) – f(z_0) – \lambda(z-z_0)}{z-z_0} = 0\\ & \Longleftrightarrow \quad \lim_{z\to z_0} \frac{| \, f(z) – f(z_0) – \lambda(z-z_0)\,|}{|\,z-z_0\,|} = 0, \tag{18.12} \end{align*} en cuyo caso $\lambda = f'(z_0)$.

De acuerdo con todo lo anterior, tenemos que la existencia de los límites dados en (18.8) y (18.12), así como el cumplimiento de las ecuaciones de C-R, nos deja ver que hay una estrecha relación entre las definiciones de diferenciabilidad real, para una función vectorial de dos variables, y de diferenciabilidad compleja.

Sean $U\subset\mathbb{C}$ un conjunto abierto y $f(z)=u(x,y)+iv(x,y)$ una función definida en $U$ y consideremos que $z=x+iy=(x,y)\in U$.

Si $f$ es una función analítica en $z_0\in U$, entonces existe $\lambda=a+ib\in\mathbb{C}$ tal que se cumple (18.12). Notemos que: \begin{align*} \lambda(z-z_0) &= (a+ib)\left[(x-x_0)+i(y-y_0)\right]\\ & = \left[a(x-x_0) – b(y-y_0)\right] + i \left[b(x-x_0) + a(y-y_0)\right], \end{align*} por lo que, considerando la transformación lineal dada por (18.11), tenemos que: \begin{equation*} M_\lambda(z-z_0) = \left(a(x-x_0) – b(y-y_0), b(x-x_0) + a(y-y_0)\right), \end{equation*} entonces: \begin{align*} 0 & = \lim_{z\to z_0} \frac{| \, f(z) – f(z_0) – \lambda(z-z_0)\,|}{|\,z-z_0\,|}\\ & = \lim_{z \to z_0} \frac{\left\| f(z) – f(z_0) – M_\lambda(z-z_0) \right\|}{\left\| z-z_0 \right\|}, \end{align*} por lo que $f$ es diferenciable, en el sentido real como función de $\mathbb{R}^2$ a $\mathbb{R}^2$. Más aún, la matriz $A$ que representa a la transformación lineal $M_\lambda$, en la base canónica de $\mathbb{R}^2$, debe ser igual a la matriz Jacobiana de $f$ en $z_0$, entonces considerando (18.10) tenemos que: \begin{equation*} \begin{pmatrix} a & -b\\ b & a \end{pmatrix} = \left(\begin{matrix} u_x(z_0) & u_y(z_0)\\ \\ v_x(z_0) & v_y(z_0) \end{matrix} \right), \end{equation*} de donde se siguen las ecuaciones de C-R y se cumple que $\lambda = f'(z_0) = u_x(z_0) + iv_x(z_0) = v_y(z_0) – i u_x(z_0)$.

Si suponemos ahora que $f$, como función de $\mathbb{R}^2$ a $\mathbb{R}^2$, es diferenciable en el sentido real y que se satisfacen las ecuaciones de C-R, entonces tenemos que se cumple (18.8).

Considerando a la matriz Jacobiana que representa a la transformación lineal $D_{f(z_0)}$, dada en (18.8), como se cumplen las ecuaciones de C-R, tenemos que dicha matriz es de la forma: \begin{equation*} \left(\begin{matrix} u_x(z_0) & -u_y(z_0)\\ \\ u_y(z_0) & u_x(z_0) \end{matrix} \right) = \begin{pmatrix} a & -b\\ b & a \end{pmatrix}, \end{equation*} para algunos $a,b\in\mathbb{R}$.

Dado que la transformación lineal $D_{f(z_0)}$ es única y la matriz que la representa es igual a la de la transformación dada en (18.11), entonces debe suceder que $D_{f(z_0)} = M_\lambda$, para $\lambda = a+ib\in\mathbb{C}$, es decir que se trata de la multiplicación por el número complejo $\lambda$, entonces: \begin{align*} 0 & = \lim_{z \to z_0} \frac{\| f(z) – f(z_0) – D_{f(z_0)}(z-z_0)\|}{\left\| z-z_0 \right\|}\\ & = \lim_{z\to z_0} \frac{| \, f(z) – f(z_0) – \lambda(z-z_0)\,|}{|\,z-z_0\,|}\ \end{align*}

Con lo anterior hemos probado el siguiente resultado.

Teorema 18.3.
Sean $U\subset\mathbb{C}$ un conjunto abierto y $f(z) = u(x,y) + iv(x,y)$ una función compleja definida en $U$. Las siguientes condiciones son equivalentes:

  1. $f$ es diferenciable en $z_0\in U$, en el sentido complejo.
  2. $f$ es diferenciable en $z_0=(x_0,y_0) \in U$, en el sentido real, pensada como una función de $\mathbb{R}^2$ a $\mathbb{R}^2$, y se satisfacen las ecuaciones de C-R en $z_0$.

$\blacksquare$

Ejemplo 18.4.
Sea $z=x+iy\in\mathbb{C}$ y sea $f:\mathbb{C} \to \mathbb{C}$ una función compleja dada por $f(z)=x^2-y^2+i2xy$. Veamos que $f$ es analítica en $\mathbb{C}$.

Solución. Si consideramos a $f$ como una función de $\mathbb{R}^2$ a $\mathbb{R}^2$ tenemos que $f(x,y) = (x^2 – y^2, 2xy)$, de donde se sigue que sus funciones componentes son: \begin{equation*} f_1(x,y)=u(x,y) = x^2-y^2, \quad f_2(x,y)=v(x,y) = 2xy. \end{equation*}

Dado que: \begin{align*} \frac{\partial u}{\partial x} = 2x, \quad \frac{\partial u}{\partial y} = -2y,\\ \frac{\partial v}{\partial x} = 2y, \quad \frac{\partial v}{\partial y} = 2x, \end{align*} existen y son continuas para todo $z=(x,y)\in\mathbb{R}^2$, entonces $f$ es una función diferenciable, en el sentido real, en $\mathbb{R}^2$.

Es claro que $u_x = v_y$ y $u_y = – v_x$ para todo $z=(x,y)\in\mathbb{R}^2$, por lo que de acuerdo con el teorema 18.3, concluimos que $f$ es diferenciable en todo $\mathbb{C}$ y por tanto analítica en todo punto.

Por último, tenemos que la matriz Jacobiana de dicha función compleja es: \begin{equation*} J_f = \begin{pmatrix} u_x & u_y\\ v_x & v_y \end{pmatrix} = \begin{pmatrix} u_x & -v_x\\ v_x & u_x \end{pmatrix} = \begin{pmatrix} 2x & -2y\\ 2y & 2x \end{pmatrix}, \end{equation*} para todo $z=x+iy\in\mathbb{C}$.

Entonces, para $z_0=x_0+iy_0\in\mathbb{C}$ se tiene que: \begin{equation*} f'(z_0) = u_x(x_0,y_0) + i v_x(x_0,y_0) = 2x_0 + i2y_0 = 2z_0, \end{equation*} lo cual era de esperarse ya que $f(z) = z^2 = x^2 – y^2 + i2xy$.

Observación 18.4.
Es importante notar que el resultado anterior es solo una reformulación del teorema 18.3, desde que la diferenciabilidad, en el sentido real, de una función $f:U\subset\mathbb{R}^2 \to \mathbb{R}^2$ es equivalente a la diferenciabilidad de sus funciones componentes. Sin embargo, la importancia de este resultado radica en que ahora que conocemos la matriz Jacobiana de una función analítica, pensada como una función de $\mathbb{R}^2$ a $\mathbb{R}^2$, es claro, por el ejercicio 3 de la entrada 12, que dicha matriz corresponde con la derivada compleja de una función analítica en cualquier punto. Además veremos que a través de esta representación matricial de la derivada es posible establecer algunos resultados de las funciones analíticas que veremos en la siguiente entrada.

Por otra parte, estos últimos resultados nos dejan ver que la diferenciabilidad compleja es más fuerte que la diferenciabilidad real, lo cual resulta sorprendente, pues a diferencia de algunos conceptos como el límite y la continuidad para los cuales vimos que podemos caracterizarlos a través de dos funciones reales, correspondientes con la parte real e imaginaria de la función, en el caso de la diferenciabilidad es claro que no bastará la diferenciabilidad en el sentido real de dichas funciones o de la diferenciabilidad en el sentido real de la función vectorial conformada por dichas funciones reales. Esto resulta de suma importancia pues nos permite diferenciar a las funciones complejas de las funciones vectoriales de dos variables, desde que la diferenciabilidad de las primeras implica la diferenciabilidad de las segundas, pero el recíproco no es cierto ya que se deben cumplir también las ecuaciones de C-R, que como probamos antes resultan ser una condición necesaria para la diferenciabilidad compleja y por ende para la analicidad de una función compleja.

Para convencernos de esto último, basta con considerar a la función $f(z)=\overline{z} = x-iy$. Es claro que está función no es diferenciable en el sentido complejo desde que las ecuaciones de C-R no se satisfacen en ningún punto en $\mathbb{C}$ y por tanto tampoco es analítica. Sin embargo, si la consideramos como una función de $\mathbb{R}^2$ a $\mathbb{R}^2$ es claro que dicha función sí es diferenciable en el sentido real.

Tanto el teorema 18.1 como el teorema 18.2 nos dejan ver que además de las ecuaciones de C-R, es necesario imponer una serie de hipótesis extras sobre las funciones reales $u$ y $v$, que caracterizan a una función compleja $f(z)=u(x,y)+iv(x,y)$, para garantizar la analicidad de dicha función. Cerraremos esta entrada con un notable resultado que nos muestra que la condición de continuidad de las derivadas parciales en el teorema 18.1 resulta superfluo. No daremos una prueba de este, pero puede consultarse en algún texto como Complex Analysis in One Variable de Raghavan Narasimhan e Yves Nievergelt.

Teorema 18.4. (Teorema de Looman-Menchoff.)
Sean $U\subset$ un conjunto abierto y $f(z)=u(x,y) = iv(x,y)$ una función definida en $U$. Si las funciones reales $u$ y $v$ son continuas en $U$ (es decir que $f$ es continua en $U$), las cuatro derivadas parciales $u_x$, $u_y$, $v_x$ y $v_y$ existen en $U$ y se satisfacen las ecuaciones de C-R en $U$, entonces $f$ es analítica en $U$.

Tarea moral

  1. Muestra que las siguientes funciones son diferenciables solo en los conjuntos dados y determina su derivada.
    a) $f(z) = x – iy^2$ en $S=\{z\in\mathbb{C} : \operatorname{Im}(z) = -1/2\}$.
    b) $f(z) = x^2 + iy^2$ en $S=\{z\in\mathbb{C} : \operatorname{Re}(z) = \operatorname{Im}(z)\}$.
    c) $f(z) = yx + iy^2$ en $S=\{z\in\mathbb{C} : \operatorname{Re}(z) = \operatorname{Im}(z) = 0 \}$.
    d) $f(z) = x^3+i(1-y)^3$ en $S=\{z\in\mathbb{C} : \operatorname{Re}(z) = 0 \,\, \text{y} \,\, \operatorname{Im}(z) = 1\}$.
  2. Para cada una de las siguientes funciones complejas determina el conjunto donde $f$ es diferenciable y el dominio de analicidad de $f$. Donde exista, determina su derivada.
    a) $f(z) = (x^3 + 3xy^2 – 3x) + i(y^3 + 3x^2y – 3y)$.
    b) $f(z) = 6\overline{z}^2 – 2\overline{z} – 4i|\,z\,|^2$.
    c) $f(z) = (3x^2 + 2x – 3y^2 -1) + i(6xy + 2y)$.
    d) $f(z) = \dfrac{2z^2 + 6}{z(z^2 + 4)}$.
  3. Determina el dominio de analicidad de las siguientes funciones.
    a) $f(z) = 4x^2+5x-4y^2+9+i(8xy+5y-1)$.
    b) $f(z) = 5r\operatorname{cos}(\theta) + r^4\operatorname{cos}(4 \theta) + i(5r\operatorname{sen}(\theta) + r^4 \operatorname{sen}(4 \theta))$.
    c) $f(z) = \dfrac{x^3+xy^2+x}{x^2+y^2} + i \dfrac{y^3+x^2y-y}{x^2+y^2}$.
    d) $f(z) = \dfrac{\operatorname{cos}(\theta)}{r} – i \dfrac{\operatorname{sen}(\theta)}{r}$.
    e) $f(z) = \dfrac{x-1}{(x-1)^2+y^2} – i \dfrac{y}{(x-1)^2+y^2}$.
  4. ¿Cuál debe ser el valor de las constantes reales $a,b,c$ y $d$ para que las siguientes funciones sean analíticas?
    a) $f(z) = 3x-y+5+i(ax+by-3)$.
    b) $f(z) = x^2 + axy+by^2+i(cx^2+dxy+y^2)$.
  5. Supón que $f$ es una función analítica en un conjunto abierto $U\subset\mathbb{C}$. Prueba que el determinante de su matriz Jacobiana es igual a $|f'(z)|^2$ para todo $z\in U$.
  6. Sean $f(z) = z^3$, $z_1 = 1$ y $z_2 = i$. Prueba que no existe un punto $z_0$ en el segmento de recta que une a $z_1$ y $z_2$, es decir $[z_1,z_2]$, tal que: \begin{equation*} f(z_2) – f(z_1) = f'(z_0) (z_2 – z_1). \end{equation*} Concluye que el teorema del valor medio para funciones reales no se extiende para funciones complejas.
  7. Sea $f$ una función analítica en un conjunto abierto $U\subset\mathbb{C}$. Prueba que la función $g(z)=\overline{f(\overline{z})}$ es analítica en el conjunto $U^*=\{\overline{z} : z\in U\}$.

Más adelante…

En esta entrada vimos bajo que condiciones es posible garantizar la analicidad de una función compleja $f(z)=u(x,y) + i v(x,y)$ sobre un conjunto abierto $U\subset\mathbb{C}$. Para ello recurrimos nuevamente a analizar las funciones reales $u$ y $v$, concluyendo que, además de las ecuaciones de C-R, es necesario imponer algunas condiciones extras sobre dichas funciones.

El objetivo de esta entrada fue dar algunos recíprocos parciales para el Teorema 17.1 de la entrada anterior. Es interesante notar que es posible relajar algunas condiciones sobre las funciones $u$ y $v$ para garantizar la analicidad de una función compleja, como es el caso del teorema de Looman-Menchoff.

La siguiente entrada abordaremos algunos resultados interesantes que son consecuencia directa de las ecuaciones de Cauchy-Riemann y que nos permitirán caracterizar aún más a las funciones complejas a través de su parte real e imaginaria, extendiendo algunos resultados obtenidos en nuestros cursos de Cálculo.

Entradas relacionadas

Variable Compleja I: Ecuaciones de Cauchy-Riemann. Condiciones necesarias para la diferenciabilidad compleja.

Por Pedro Rivera Herrera

2 respuestas

Introducción

Hasta ahora hemos visto que toda función compleja $f(z)$ diferenciable es continua, más aún sabemos que toda función compleja continua es de la forma: \begin{equation*} f(z) = u(x,y) + i v(x,y), \end{equation*} donde $u(x,y)$ y $v(x,y)$ son funciones reales continuas de variables $x,y$, por lo que resulta natural preguntarnos acerca de qué condiciones deben cumplir dichas funciones para que una función compleja $f(z)$ sea analítica. La respuesta a esta pregunta esta dada por las ecuaciones de Cauchy-Riemann, a las cuales nos referiremos simplemente como las ecuaciones de C-R. Dichas ecuaciones aparecieron por primera vez en 1821 en los primeros trabajos del matemático fránces Augustin Louis Cauchy sobre integrales de funciones complejas. Su relación con la existencia de la derivada compleja apareció hasta 1851 en la tesis doctoral del matemático alemán Bernhard Riemann.

Como veremos a lo largo de las siguientes entradas, las ecuaciones de C-R resultan ser un pilar en la teoría de las funciones complejas, por lo que nuestro objetivo será deducirlas y obtener una serie de resultados que nos permitan caracterizar a las funciones analíticas mediante dichas ecuaciones.

Recordemos las siguientes definiciones vistas en nuestros cursos de cálculo.

Definición 17.1. (Derivada parcial.)
Supongamos que $u: \mathbb{R}^2 \to \mathbb{R}$ es una función real de variables reales, $x,y$, definida en un conjunto abierto no vacío $U\subset \mathbb{R}^2$. Si consideramos a la variable $y$ como constante, entonces podemos pensar a $u$ como una función únicamente de $x$ y derivar con respecto a $x$. Entonces: \begin{equation*} \frac{\partial u }{\partial x}(x,y) = \lim_{h \to 0} \frac{u(x+h, y) – u(x,y)}{h}. \end{equation*}

En caso de existir dicho límite lo llamaremos la derivada parcial de $u$ con respecto a $x$ y es denotada como $\frac{\partial u }{\partial x}$ o $u_x$. Dicha derivada resulta ser una función evaluada en el punto $(x,y)$, lo cual se suele omitir por simplicidad en la notación.

Análogamente, fijando a $x$ y considerando a $u(x,y)$ como una función de $y$, tenemos al derivar con respecto a $y$ la derivada parcial de $u$ con respecto a $y$, es decir: \begin{equation*} \frac{\partial u }{\partial y}(x,y) = \lim_{h \to 0} \frac{u(x, y+h) – u(x,y)}{h}. \end{equation*}

Definición 17.2. (Funciones clase $C^k$.)
Si $U\subset\mathbb{R}^2$ es un conjunto abierto y $u:U\to\mathbb{R}$ es una función, entonces $u$ es llamada de clase $C^1$ o continuamente diferenciable en $U$ si $\partial u/\partial x$ y $\partial u/\partial y$ existen y son continuas en $U$. Lo anterior se denota de forma abreviada como $u\in C^1(U)$.

De forma general si $k\in\mathbb{N}$, entonces una función real $u$ definida en $U\subset\mathbb{R}^2$, es llamada de clase $C^k$ o $k$-veces continuamente diferenciable si todas las derivadas parciales hasta el orden $k$ existen y son continuas en $U$. En dicho caso escribimos $u\in C^k(U)$. En particular, diremos que una función $u$ es clase $C^0$ si simplemente es una función continua.

Entonces, para $U\subset \mathbb{C}$ abierto, una función $f(z) = u(x,y) + i v(x,y)$ definida en $U$, es llamada de clase $C^k$ si $u$ y $v$ son de clase $C^k$.

Observación 17.1.
A partir de ahora usaremos la notación $U$ para denotar conjuntos abiertos en $\mathbb{C}$ y $D$ para denotar dominios o regiones en $\mathbb{C}$, estos conceptos se abordaron en la Unidad 1: Introducción y preliminares.

De acuerdo con la observación 16.2 sabemos que si una función $f:U\to\mathbb{C}$ es diferenciable en un punto $z_0\in U$, entonces el límite: \begin{equation*} f'(z_0) = \lim_{z \to z_0} \dfrac{f(z) – f(z_0)}{z-z_0} = \lim_{h \to 0} \dfrac{f(z_0 + h) – f(z_0)}{h}, \end{equation*} existe y es único sin importar como $h$ se aproxime a $0$ en el plano complejo. Sin embargo es importante notar que al igual que en el caso de funciones reales, podemos considerar a dos direcciones privilegiadas cuando $h \to 0$, figura 73, las cuales son:

  1. a lo largo de un eje paralelo al eje real, es decir cuando $h\in \mathbb{R}$,
  2. a lo largo de un eje paralelo al eje imaginario, es decir cuando $h=ki\in\mathbb{C}$, con $k\in\mathbb{R}$, es un número complejo puro.
Figura 73: Gráfica de las dos direcciones privilegiadas por las que $z$ se aproxima a $z_0$ al calcular $f'(z_0)$.

Veamos entonces qué sucede al calcular el límite que define a $f'(z)$ si consideramos las direcciones privilegiadas descritas previamente. Supongamos que $f(z) = u(x,y) + iv(x,y)$ es una función diferenciable en un punto $z_0=x_0+iy_0\in U$, con $U \subset \mathbb{C}$ abierto.

Si $h$ es real, entonces: \begin{align*} f'(z_0) &= \lim_{h \to 0} \frac{f(z_0+h) – f(z_0)}{h}\\ & = \lim_{h \to 0} \left[ \frac{u(x_0+h,y_0) – u(x_0,y_0)}{h} + i \frac{v(x_0+h,y_0) – v(x_0,y_0)}{h}\right]\\ & = \lim_{h \to 0} \frac{u(x_0+h,y_0) – u(x_0,y_0)}{h} + i \lim_{h \to 0} \frac{v(x_0+h,y_0) – v(x_0,y_0)}{h}\\ & = \frac{\partial u}{ \partial x}(x_0,y_0) + i \frac{\partial v}{ \partial x}(x_0,y_0)\\ & =: \frac{\partial f}{\partial x}(x_0,y_0) = f_x(z_0). \tag{17.1} \end{align*}

Si $h$ es un número imaginario puro, es decir $h=ik$, con $k$ real, entonces $h\to 0$ si y solo si $k\to 0$, por lo que: \begin{align*} f'(z_0) &= \lim_{h \to 0} \frac{f(z_0+h) – f(z_0)}{h}\\ & = \lim_{k \to 0} \left[ \frac{u(x_0,y_0+k) – u(x_0,y_0)}{ik} + i \frac{v(x_0,y_0+k) – v(x_0,y_0)}{ik}\right]\\ & = \frac{1}{i}\lim_{k \to 0} \frac{u(x_0,y_0+k) – u(x_0,y_0)}{k} + \lim_{k \to 0} \frac{v(x_0,y_0+k) – v(x_0,y_0)}{k}\\ & = -i \frac{\partial u}{ \partial y}(x_0,y_0) + \frac{\partial v}{ \partial y}(x_0,y_0)\\ & =: -i\frac{\partial f}{\partial y}(x_0,y_0) = -i f_y(z_0). \tag{17.2} \end{align*}

De ambos casos es claro que la existencia de las cuatro derivadas parciales: \begin{equation*} \frac{\partial u}{\partial x}, \quad \frac{\partial u}{\partial y}, \quad \frac{\partial v}{\partial x}, \quad \frac{\partial v}{\partial y} \end{equation*} en el punto $(x_0,y_0)$, está garantizada por la existencia del límite que define a la derivada compleja en el punto $z_0 = x_0 +iy_0 \in U$.

Observación 17.1.
Hemos introducido en las últimas igualdades de las ecuaciones (17.1) y (17.2) una notación usual en algunos textos para referirnos a la derivada de una función compleja en términos de las derivadas parciales de las funciones $u$ y $v$, es importante no confundirnos con dicha notación la cual se usará de manera indistinta en el curso.

Dado que $f'(z_0)$ existe sin importar la dirección en que $h$ se aproxime a $0$, entonces los dos límites dados en (17.1) y (17.2) deben ser iguales, es decir: \begin{equation*} f'(z_0) = \frac{\partial u}{ \partial x}(x_0,y_0) + i \frac{\partial v}{ \partial x}(x_0,y_0) = \frac{\partial v}{ \partial y}(x_0,y_0) -i \frac{\partial u}{ \partial y}(x_0,y_0), \tag{17.3} \end{equation*} o equivalentemente: \begin{equation*} f'(z_0) = f_x(z_0) = -i f_y(z_0). \tag{17.4} \end{equation*}

Igualando las partes reales e imaginarias de estos dos números complejos tenemos que: \begin{equation*} \frac{\partial u}{ \partial x} (x_0, y_0)= \frac{\partial v}{ \partial y}(x_0, y_0), \quad \text{y} \quad \frac{\partial u}{ \partial y}(x_0, y_0) = – \frac{\partial v}{ \partial x}(x_0, y_0). \tag{17.5} \end{equation*}

Al par de ecuaciones diferenciales parciales dado en (17.5) se les conoce como las ecuaciones de Cauchy-Riemann.

Con lo anterior hemos probado el siguiente resultado.

Teorema 17.1. (Ecuaciones de Cauchy-Riemann.)
Sean $U\subset \mathbb{C}$ un conjunto abierto y $f:U\to \mathbb{C}$ una función. Si $f(z) = u(x,y) + iv(x,y)$ es analítica en un punto $z_0=x_0 +iy_0\in U$, entonces existen las derivadas parciales: \begin{equation*} \frac{\partial u}{\partial x}, \quad \frac{\partial u}{\partial y}, \quad \frac{\partial v}{\partial x}, \quad \frac{\partial v}{\partial y} \end{equation*} en $(x_0,y_0)$ y satisfacen las ecuaciones de Cauchy-Riemann (17.5) en dicho punto. En tal caso se tiene que: \begin{equation*} f'(z_0) = \frac{\partial u}{\partial x}(x_0,y_0) + i \frac{\partial v}{\partial x}(x_0,y_0) = \frac{\partial v}{\partial y}(x_0,y_0) – i \frac{\partial u}{\partial y}(x_0,y_0). \end{equation*}

$\blacksquare$

Corolario 17.1.
Si $f(z)=u(x,y) + iv(x,y)$ es una función analítica en un conjunto abierto $U\subset\mathbb{C}$, entonces las ecuaciones de C-R se satisfacen en todo punto de $U$.

$\blacksquare$

De acuerdo con el corolario 16.1 de la entrada anterior, sabemos que todo polinomio complejo es una función entera, es decir, analítica en todo $\mathbb{C}$, por lo que de acuerdo con el corolario 17.1 se deben cumplir las ecuaciones de C-R para todo $z=x+iy\in\mathbb{C}$.

Ejemplo 17.1
Consideremos al polinomio complejo $f(z) = 2z^2 + 3z$, para $z=x+iy\in\mathbb{C}$, veamos que se satisfacen las ecuaciones de C-R en $\mathbb{C}$ y obtengamos la derivada de $f$.

Solución. Tenemos que: \begin{equation*} f(z) = 2(x^2 – y^2) + 3x + i(4xy + 3y), \end{equation*} de donde $u(x,y) = 2(x^2 – y^2) + 3x$ y $v(x,y) = 4xy + 3y$.

Entonces para todo $z=x+iy\in\mathbb{C}$ se satisfacen las ecuaciones de C-R: \begin{align*} \frac{\partial u}{\partial x} = 4x + 3 = \frac{\partial v}{\partial y},\\ \frac{\partial u}{\partial y} = -4y = – \frac{\partial v}{\partial x}. \end{align*}

Por otra parte, de acuerdo con el teorema 1 tenemos que la derivada de $f$ es: \begin{equation*} f'(z) = 4x+3 + i4y = 4(x+iy) + 3 = 4z + 3. \end{equation*}

Observación 17.3.
El teorema 17.1 establece que una condición necesaria para que una función $f(z)=u(x,y)+i v(x,y)$ sea analítica en un punto $z_0\in U \subset\mathbb{C}$ es que las ecuaciones de C-R se satisfagan en dicho punto.

La importancia del teorema 17.1 y del corolario 17.1 radica en que tenemos ahora un criterio para determinar cuando una función no es analítica por medio de las ecuaciones de C-R. Para mostrar esto consideremos los siguientes ejemplos.

Ejemplo 17.2.
De acuerdo con el ejemplo 16.3 de la entrada anterior, sabemos que las funciones $f(z) = \overline{z}$ y $g(z) = \operatorname{Re}(z)$ no son analíticas en ningún punto de $\mathbb{C}$. Utilizando la contrapuesta del corolario 17.1 procedemos a verificar nuestro resultado.

Solución. Es claro que ambas funciones están definidas en todo $\mathbb{C}$. Sea $z=x+iy\in\mathbb{C}$.

a) Para $f(z) = \overline{z} = x – iy$ tenemos que $u(x,y) = x$ y $v(x,y) = -y$, por lo que: \begin{align*} \frac{\partial u}{\partial x} = 1 \quad \text{y} \quad \frac{\partial u}{\partial y} = 0,\\ \frac{\partial v}{\partial x} = 0 \quad \text{y} \quad \frac{\partial v}{\partial y} = -1. \end{align*} Es claro que $\partial u/\partial x \neq \partial v/\partial y$ para todo $z = x+iy \in \mathbb{C}$, por lo que $f$ no es analítica en ningún punto.

b) Por otra parte, para $g(z) = \operatorname{Re}(z) = x$ tenemos que $u(x,y) = x$ y $v(x,y) = 0$, por lo que: \begin{align*} \frac{\partial u}{\partial x} = 1 \quad \text{y} \quad \frac{\partial u}{\partial y} = 0,\\ \frac{\partial v}{\partial x} = 0 \quad \text{y} \quad \frac{\partial v}{\partial y} = 0. \end{align*} Tenemos que $\partial u/\partial x \neq \partial v/\partial y$ y $\partial u/\partial y \neq -\partial v/\partial x$ para todo $z = x+iy \in \mathbb{C}$, por lo que $f$ no es analítica en ningún punto.

Ejemplo 17.3.
Sea $z=x+iy\in\mathbb{C}$. Veamos que la función compleja $f(z) = 2x^2 +y +i(y^2-x)$ no es analítica en ningún punto.

Solución. Notemos que $u(x,y) = 2x^2 + y$ y $v(x,y) = y^2 – x$, entonces: \begin{equation*} \frac{\partial u}{\partial x} = 4x \quad \text{y} \quad \frac{\partial u}{\partial y} = 1, \end{equation*} \begin{equation*} \frac{\partial v}{\partial x} = -1 \quad \text{y} \quad \frac{\partial v}{\partial y} = 2y. \end{equation*}

Es claro que $\partial u/\partial y = -\partial v/\partial x$ para todo $z=x+iy \in \mathbb{C}$, mientras que la igualdad $\partial u/\partial x = \partial v/\partial y$ se satisface solamente en la recta $y=2x$. Sin embargo, para todo punto $z=x+iy$ sobre dicha recta, no existe un disco abierto alrededor de $z$ en el cual $f$ sea diferenciable, por lo que $f$ no es analítica en ningún punto.

Es importante notar que aunque se satisfagan las ecuaciones de C-R en un punto $z_0= x_0+iy_0\in D$, esto no es suficiente para garantizar la existencia de $f'(z_0)$ en $D$, desde que existen muchas otras direcciones por las que $z$ se aproxima a $z_0$ al calcular el límite que define a $f'(z_0)$. Consideremos el siguiente ejemplo para verificar lo anterior.

Ejemplo 17.4.
Sea $z=x+iy$. Veamos que la función: \begin{equation*} f(z)= \left\{\begin{array}{lcc} \dfrac{x^3(1+i) – y^3(1-i)}{x^2+y^2}& \text{si} & z\neq 0, \\ 0 & \text{si} & z = 0, \end{array} \right. \end{equation*} es continua en $z=0$ y que en dicho punto se satisfacen las ecuaciones de C-R, pero $f'(0)$ no existe.

Solución. Sea $f(z)=u(z)+iv(z)$, entonces para $z\neq 0$ tenemos que: \begin{equation*} u(x,y) = \frac{x^3 – y^3}{x^2+y^2}, \quad v(x,y) = \frac{x^3 + y^3}{x^2+y^2}, \end{equation*} con $x\neq 0$ y $y\neq 0$.

Primeramente verifiquemos que $f(z)$ es continua en todo $\mathbb{C}$. Es claro que si $z\neq 0$, entonces las funciones racionales $u(x,y)$ y $v(x,y)$ están bien definidas y son continuas, por lo que en dicho caso $f(z)$ es continua. Probemos ahora que $f(z)$ es continua en $z=0$. Utilizando coordenadas polares tenemos que: \begin{equation*} u(r,\theta) = r\left(\operatorname{cos}^3(\theta) – \operatorname{sen}^3(\theta)\right), \quad v(r,\theta) = r\left(\operatorname{cos}^3(\theta) + \operatorname{sen}^3(\theta)\right). \end{equation*}

Notemos que si $z\to 0$, entonces $r \to 0$, para cualquier argumento $\theta$, por lo que: \begin{equation*} \lim_{r \to 0} u(r,\theta) = \lim_{r \to 0} v(r,\theta) = 0, \end{equation*} entonces: \begin{equation*} \lim_{z \to 0} f(z) = 0 = f(0), \end{equation*} por lo que $f(z)$ es continua en $z=0$ y por tanto es continua en todo $\mathbb{C}$.

Veamos ahora que en $z=0$ las ecuaciones de C-R se satisfacen. Si $z=0$, entonces: \begin{align*} f(0) = 0 \quad & \Longleftrightarrow \quad u(0,0) + iv(0,0) = 0\\ & \Longleftrightarrow \quad u(0,0) = v(0,0) = 0. \end{align*} Por definición tenemos que: \begin{align*} \frac{\partial u}{\partial x} (0,0) & = \lim_{h\to 0}\frac{u(h,0) – u(0,0)}{h}\\ & = \lim_{h\to 0}\frac{h – 0}{h}\\ & = 1. \end{align*} \begin{align*} \frac{\partial u}{\partial y} (0,0) & = \lim_{h\to 0}\frac{u(0,h) – u(0,0)}{h}\\ & = \lim_{h\to 0}\frac{-h – 0}{h}\\ & = -1. \end{align*} Mientras que: \begin{align*} \frac{\partial v}{\partial x} (0,0) & = \lim_{h\to 0}\frac{v(h,0) – v(0,0)}{h}\\ & = \lim_{h\to 0}\frac{h – 0}{h}\\ & = 1. \end{align*} \begin{align*} \frac{\partial v}{\partial y} (0,0) & = \lim_{h\to 0}\frac{v(0,h) – v(0,0)}{h}\\ & = \lim_{h\to 0}\frac{h – 0}{h}\\ & = 1. \end{align*} Entonces, en el origen tenemos que: \begin{equation*} \frac{\partial u}{ \partial x} = \frac{\partial v}{ \partial y}, \quad \frac{\partial v}{ \partial x} = -\frac{\partial u}{ \partial y}, \end{equation*} por lo que en $z=0$ se satisfacen las ecuaciones de C-R. Sin embargo, $f(z)$ no es diferenciable en dicho punto.

Para $z=x+iy$ tenemos que: \begin{align*} f'(0) & = \lim_{z \to 0} \frac{f(z) – f(0)}{z}\\ & = \lim_{z \to 0} \frac{f(z) – 0}{z}\\ & = \lim\limits_{\begin{subarray}{l} x \to 0\\ y \to 0 \end{subarray}} \frac{(x^3 – y^3) + i (x^3 + y^3)}{(x^2+y^2)(x+iy)}. \end{align*} Notemos que si $z$ se aproxima $0$ a lo largo de la recta $y=x$, entonces: \begin{align*} f'(0) & = \lim_{z \to 0} \frac{f(z) – f(0)}{z}\\ & = \lim_{x \to 0} \frac{2ix^3}{2x^3(1+i)}\\ & = \frac{i}{1+i}. \end{align*} Por otra parte, si $z$ se aproxima $0$ a lo largo del eje real $x$, es decir si $y=0$, entonces: \begin{align*} f'(0) & = \lim_{z \to 0} \frac{f(z) – f(0)}{z}\\ & = \lim_{x \to 0} \frac{x^3(1+i)}{x^3}\\ & = 1+i. \end{align*} Dado que estos límites son distintos, entonces $f'(0)$ no existe y por tanto $f(z)$ no es diferenciable en $z=0$.

De acuerdo con la proposición 16.1 de la entrada anterior, sabemos que una consencuencia de la analicidad de una función $f$ en un punto $z_0 \in U\subset\mathbb{C}$, es la continuidad de la función $f$ en dicho punto. Sin embargo, el ejemplo 17.4 muestra que el recíproco de dicha proposición no es cierto, pues la función $f(z)$ de dicho ejemplo es continua en $z_0 = 0$, pero no es analítica en dicho punto.

Observación 17.4.
De nuestros cursos de geometría sabemos que al trabajar con coordenadas polares es posible establecer una transformación biunívoca entre las coordenadas polares y las coordenadas cartesianas mediante la transformación: \begin{align*} T: (0,\infty) \times (-\pi,\pi] \to \mathbb{R}^2\setminus\{(0,0)\},\\ T(r,\theta)=(r\operatorname{cos}(\theta), r\operatorname{sen}(\theta)). \end{align*} Por ejemplo, para el conjunto de puntos: \begin{equation*} U^* = \left\{(r,\theta) : 1\leq r \leq 2 \, \, \text{y} \,\, 0\leq \theta \leq \pi/2\right\}, \end{equation*} se tiene que $T(U^*) = U$, con: \begin{equation*} U = \left\{(x,y) : 1/2 \leq x \leq 1 \, \, \text{y} \,\, \sqrt{1-x^2} \leq y \leq \sqrt{3} x \right\}\cup \left\{(x,y) : 1 \leq x \leq 2 \, \, \text{y} \,\, 0 \leq y \leq \sqrt{4-x^2}\right\}. \end{equation*}

De acuerdo con la observación 12.5, al considerar a $z\in\mathbb{C}$, $z\neq 0$, en su forma polar, es posible expresar a una función compleja $f(z)$ en términos de su parte real e imaginaria, las cuales son funciones reales de las variables $r$ y $\theta$, por lo que considerando la transformación anterior, resulta sencillo verificar el siguiente resultado.

Proposición 17.1. (Forma polar de las ecuaciones de C-R.)
Sean $U\subset\mathbb{C}\setminus{0}$ un conjunto abierto y $f\in\mathcal{F}(U)$ una función. Si la función $f(z)=u(x,y) + iv(x,y)$ es analítica en $U$, entonces considerando la transformación dada por $x=r\operatorname{cos}(\theta)$, $y=r\operatorname{sen}(\theta)$, para $(r,\theta)\in U^*$ y $U^* \subset (0,\infty)\times(-\pi, \pi]$, se tiene que las ecuaciones de Cauchy-Riemann en su forma polar están dadas por: \begin{equation*} \frac{\partial u}{\partial r} = \frac{1}{r} \frac{\partial v}{\partial \theta} \quad \text{y} \quad \frac{\partial v}{\partial r} = -\frac{1}{r} \frac{\partial u}{\partial \theta}, \tag{17.6} \end{equation*} las cuales existen para cada punto de $U$.

Más aún, en consecuencia con el teorema 1, se tiene que para $z_0 = r_0 \operatorname{cis}(\theta_0) \in U$, un punto donde $f$ es analítica, se cumple que: \begin{align*} f'(z_0) & = \operatorname{cis}(-\theta) \left[ \frac{\partial u}{\partial r} (r_0, \theta_0)+ i \frac{\partial v}{\partial r}(r_0, \theta_0)\right]\\ & = \left[\operatorname{cos}(\theta) – i \operatorname{sen}(\theta) \right]\left[ u_r(r_0, \theta_0)+ i v_r(r_0, \theta_0)\right]. \end{align*}

Demostración. Se deja como ejercicio al lector.

$\blacksquare$

Ejemplo 17.5.
Consideremos a la función $f(z) = \dfrac{1}{z^2}$. De acuerdo con el corolario 16.1 sabemos que dicha función es analítica en $\mathbb{C}\setminus\{0\}$, por lo que considerando a $z\neq 0$ en coordenadas polares podemos verificar que se cumplen las ecuaciones de C-R en su forma polar para todo $(r,\theta) \in (0,\infty) \times (-\pi,\pi]$ o equivalentemente, por la observación 17.4, para todo $z \in \mathbb{C}\setminus\{0\}$.

Solución.
Sea $z=r\operatorname{cis}(\theta) \neq 0$, con $r = |\,z\,|$ y $\theta = \operatorname{Arg} z$. Por la fórmula de De Moivre tenemos que: \begin{align*} f(z) = \frac{1}{z^2} & = \frac{1}{\left[r\operatorname{cis}(\theta)\right]^2}\\ & = \frac{1}{r^2\left[\operatorname{cos}(2\theta) + \operatorname{sen}(2\theta)\right]}\\ & = \frac{\operatorname{cos}(2\theta) – i \operatorname{sen}(2\theta)}{r^2}\\ & = \frac{\operatorname{cos}(2\theta)}{r^2} – i \frac{\operatorname{sen}(2\theta)}{r^2}. \end{align*} Entonces: \begin{align*} u(r,\theta) = \frac{\operatorname{cos}(2\theta)}{r^2},\\ v(r,\theta) = – \frac{\operatorname{sen}(2\theta)}{r^2}. \end{align*} Tenemos que para todo $(r,\theta)\in(0,\infty)\times (-\pi,\pi]$ se cumple que: \begin{align*} \frac{\partial u}{\partial r} = – \frac{2\operatorname{cos}(\theta)}{r^3} = \frac{1}{r} \frac{\partial v}{\partial \theta},\\ \frac{\partial v}{\partial r} = \frac{2\operatorname{sen}(\theta)}{r^3} = -\frac{1}{r} \frac{\partial u}{\partial \theta}. \end{align*} Por lo tanto, para todo $z=r\operatorname{cis}(\theta) \in \mathbb{C}\setminus\{0\}$ se satisfacen las ecuaciones de C-R.

Es claro que utilizando las reglas de derivación vistas en la entrada anterior es posible obtener la derivada de $f$ para todo $z\neq 0$, sin embargo utilizando la proposición 17.1 tenemos que: \begin{align*} f'(z) & = \operatorname{cis}(-\theta) \left[ \frac{\partial u}{\partial r}+ i \frac{\partial v}{\partial r}\right]\\ & = \left[\operatorname{cos}(\theta) – i \operatorname{sen}(\theta) \right]\left[ – \frac{2\operatorname{cos}(\theta)}{r^3} + i \frac{2\operatorname{sen}(\theta)}{r^3}\right]\\ & = – \frac{2}{r^3} \left[ \left( \operatorname{cos}^3(\theta) -3\operatorname{sen}^2(\theta) \operatorname{cos}(\theta)\right) – i \left( 3\operatorname{cos}^2(\theta) \operatorname{sen}(\theta) – \operatorname{sen}^3(\theta) \right)\right]\\ & = – \frac{2}{r^3} \left[ \operatorname{cos}(-3\theta) + i \operatorname{sen}(-3\theta)\right]\\ & = – \frac{2}{r^3 \operatorname{cis}(3\theta)}\\ & = – \frac{2}{\left( r \operatorname{cis}(\theta)\right)^3} = – \frac{2}{z^3}. \end{align*}

Ejemplo 17.6.
De acuerdo con el ejemplo 16.5 sabemos que $f_0$, es decir la rama principal de la función multivaluada $F(z)=\sqrt{z}$, es analítica en el dominio $D=\mathbb{C}\setminus(-\infty,0]$. Veamos que se cumplen las ecuaciones de C-R en $D$.

Solución. Sea $z\in D$. Escribiendo $z = r\operatorname{cis}(\theta)$, con $r=|\,z\,|$ y $\theta =\operatorname{Arg}(z)$, entonces: \begin{align*} f_0(z) & = \sqrt{r}\operatorname{cis}\left(\frac{\theta}{2}\right)\\ & = \sqrt{r}\operatorname{cos}\left(\frac{\theta}{2}\right) + i \sqrt{r}\operatorname{sen}\left(\frac{\theta}{2}\right)\\ & = u(r,\theta) + iv(r,\theta). \end{align*}

Es claro que para todo $(r,\theta)\in(0,\infty)\times (-\pi,\pi)$ se cumple que: \begin{align*} \frac{\partial u}{\partial r} = \frac{\operatorname{cos}\left(\frac{\theta}{2}\right)}{2\sqrt{r}} = \frac{1}{r} \frac{\partial v}{\partial \theta},\\ \frac{\partial v}{\partial r} = \frac{\operatorname{sen}\left(\frac{\theta}{2}\right)}{2\sqrt{2}} = -\frac{1}{r} \frac{\partial u}{\partial \theta}. \end{align*}

Por lo que para todo $z = r\operatorname{cis}(\theta)\in D$ se cumplen las ecuaciones de C-R.

Tarea moral

  1. Demuestra la proposición 17.1.
    Hint: Observa que $u(x,y) = u(r\operatorname{cos}(\theta), r\operatorname{sen}(\theta))$ y $v(x,y) = v(r\operatorname{cos}(\theta), r\operatorname{sen}(\theta))$. Dado que la función $f$ es analítica en el abierto $U$, por el corolario 1 se satisfacen las ecuaciones de C-R en $U$, por lo que utilizando la regla de la cadena para funciones reales de dos variables se tiene que: \begin{align*} \frac{\partial u}{\partial r} = \frac{\partial u}{\partial x} \frac{\partial x}{\partial r} + \frac{\partial u}{\partial y} \frac{\partial y}{\partial r}, \quad \frac{\partial u}{\partial \theta} = \frac{\partial u}{\partial x} \frac{\partial x}{\partial \theta} + \frac{\partial u}{\partial y} \frac{\partial y}{\partial \theta},\\ \frac{\partial v}{\partial r} = \frac{\partial v}{\partial x} \frac{\partial x}{\partial r} + \frac{\partial v}{\partial y} \frac{\partial y}{\partial r}, \quad \frac{\partial v}{\partial \theta} = \frac{\partial v}{\partial x} \frac{\partial x}{\partial \theta} + \frac{\partial v}{\partial y} \frac{\partial y}{\partial \theta}. \tag{17.7} \end{align*}
  2. De las ecuaciones dadas en (17.7), resuelve para $u_x$, $u_y$, $v_x$ y $v_y$ y concluye que: \begin{align*} \frac{\partial u}{\partial x} = \frac{\partial u}{\partial r} \operatorname{cos}(\theta) – \frac{\partial u}{\partial \theta} \frac{\operatorname{sen(\theta)}}{r}, \quad \frac{\partial u}{\partial y} = \frac{\partial u}{\partial r} \operatorname{sen}(\theta) + \frac{\partial u}{\partial \theta}\frac{\operatorname{cos(\theta)}}{r},\\ \frac{\partial v}{\partial x} = \frac{\partial v}{\partial r} \operatorname{cos}(\theta) – \frac{\partial v}{\partial \theta} \frac{\operatorname{sen(\theta)}}{r}, \quad \frac{\partial v}{\partial y} = \frac{\partial v}{\partial r} \operatorname{sen}(\theta) + \frac{\partial v}{\partial \theta}\frac{\operatorname{cos(\theta)}}{r}. \end{align*} Suponiendo que el teorema 1 se cumple para la forma polar de las ecuaciones de C-R, utiliza las ecuaciones anteriores para verificar que las ecuaciones de C-R se verifican ahora para las funciones reales $u(x,y)$ y $v(x,y)$. Con esto se verifica que las ecuaciones dadas en (17.6) en efecto son la forma polar de las ecuaciones de C-R.
  3. Prueba que las siguientes funciónes no son analíticas en su dominio.
    a) $f(z) = |\,z\,|^2$, pero es diferenciable en $z=0$.
    b) $f(z) = y + ix$, para $z=x+iy\in\mathbb{C}$.
    c) $f(z) = \overline{z}^2$ para $z=x+iy\in\mathbb{C}$.
    d) $f(z) = 4z – 6 \overline{z} + 3$ para $z=x+iy\in\mathbb{C}$.
  4. Supón que $f(z) = u(x,y) + iv(x,y)$ es una función analítica en un conjunto abierto $U\subset\mathbb{C}$. Sean $h(z) = \overline{f(z)}$ y $g(z) = v(x,y) + iu(x,y)$ dos funciones complejas definidas en el mismo conjunto $U$, entonces ¿son $h$ y $g$ funciones analíticas en $U$?
  5. Sean $U\subset\mathbb{C}$ un conjunto abierto y $f(z) = u(x,y) + iv(x,y)$ una función analítica en un $U$. Prueba que:
    a) $f'(z) = u_x(z) – i u_y(z) = v_y(z) + i v_x(z)$.
    b) $|\,f'(z)\,|^2 = u_x^2 + u_y^2 = v_x^2 + v_y^2$, para todo $z=x+iy\in U$.
  6. Considera la siguiente función: \begin{equation*} f(z)= \left\{\begin{array}{lcc} \dfrac{z^5}{|\,z\,|^4}& \text{si} & z\neq 0, \\ 0 & \text{si} & z = 0. \end{array} \right. \end{equation*} Muestra que en $z=0$ la función $f$ satisface las ecuaciones de C-R, pero $f'(0)$ no existe.

Más adelante…

En esta entrada hemos deducido las ecuaciones de Cauchy-Riemann y probamos que para una función compleja $f(z) = u(x,y) + iv(x,y)$ dichas ecuaciones resultan ser un conjunto de condiciones necesarias que deben satisfacer la parte real y la parte imaginaria, $u$ y $v$ respectivamente, en un punto donde $f(z)$ es analítica. Sin embargo, vimos mediante algunos ejemplos que dichas ecuaciones no son una condición suficiente para garantizar la analicidad de una función en un conjunto abierto $U\subset\mathbb{C}$.

Lo anterior nos motiva a preguntarnos bajo qué condiciones, además de las ecuaciones de C-R, las funciones reales $u$ y $v$ nos permiten garantizar que una función compleja $f(z)$ sea analítica en $U$, lo cual responderemos en la siguiente entrada.

Entradas relacionadas