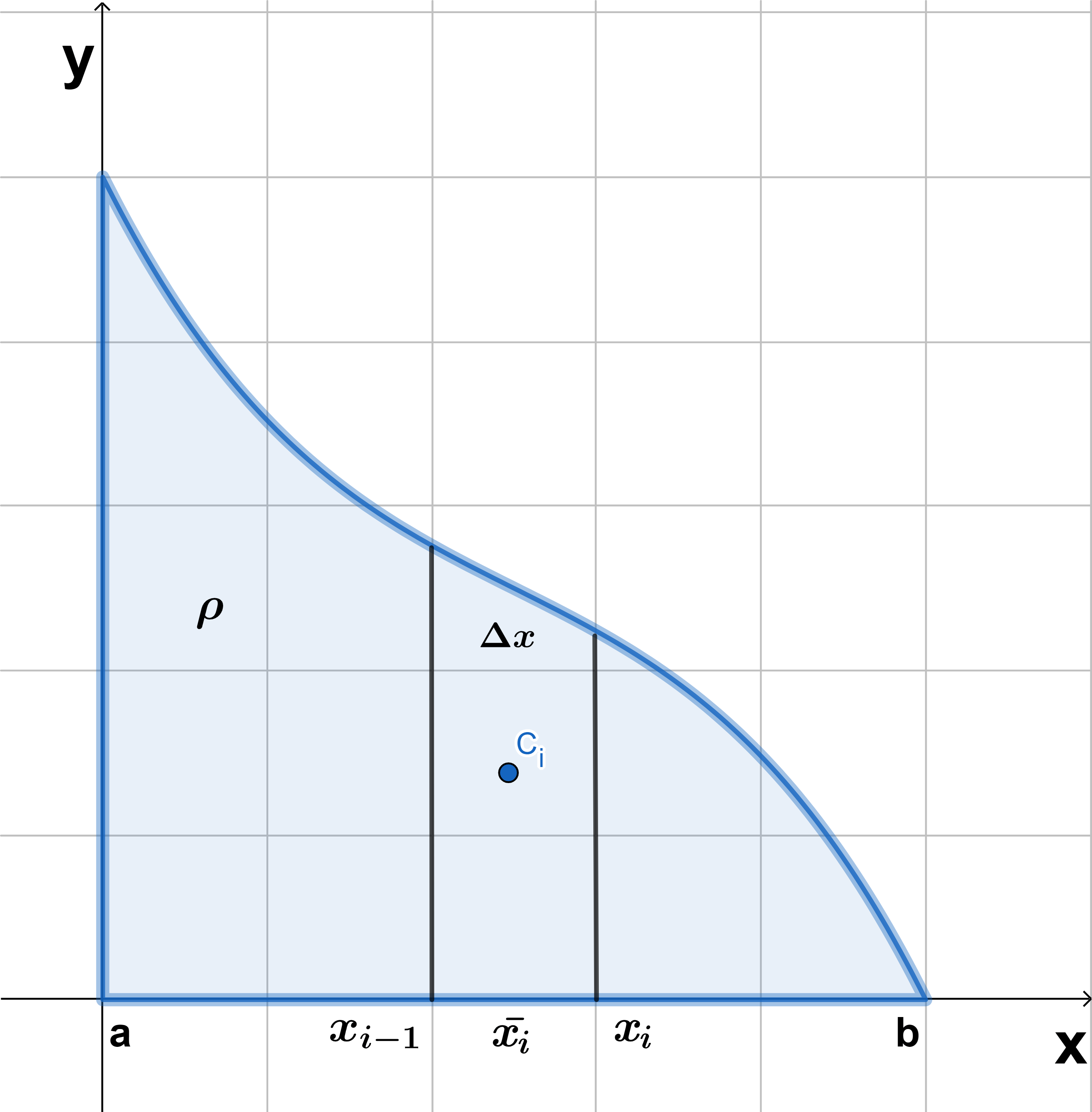Introducción
En la sección anterior vimos el teorema de Pappus-Guldin el cual nos permite calcular el centroide, área y volumen de un sólido de revolución, en esta sección veremos una aplicación en el área de la física como aplicación de la integración para el cálculo de centro de masas y momentos. Cabe destacar que estudiaremos objetos unidimensionales y bidimensionales, ya que para objetos en el espacio se necesitan integrales múltiples, lo cual, no estudiaremos en este curso.
Centro de masas y momentos (unidimensional)
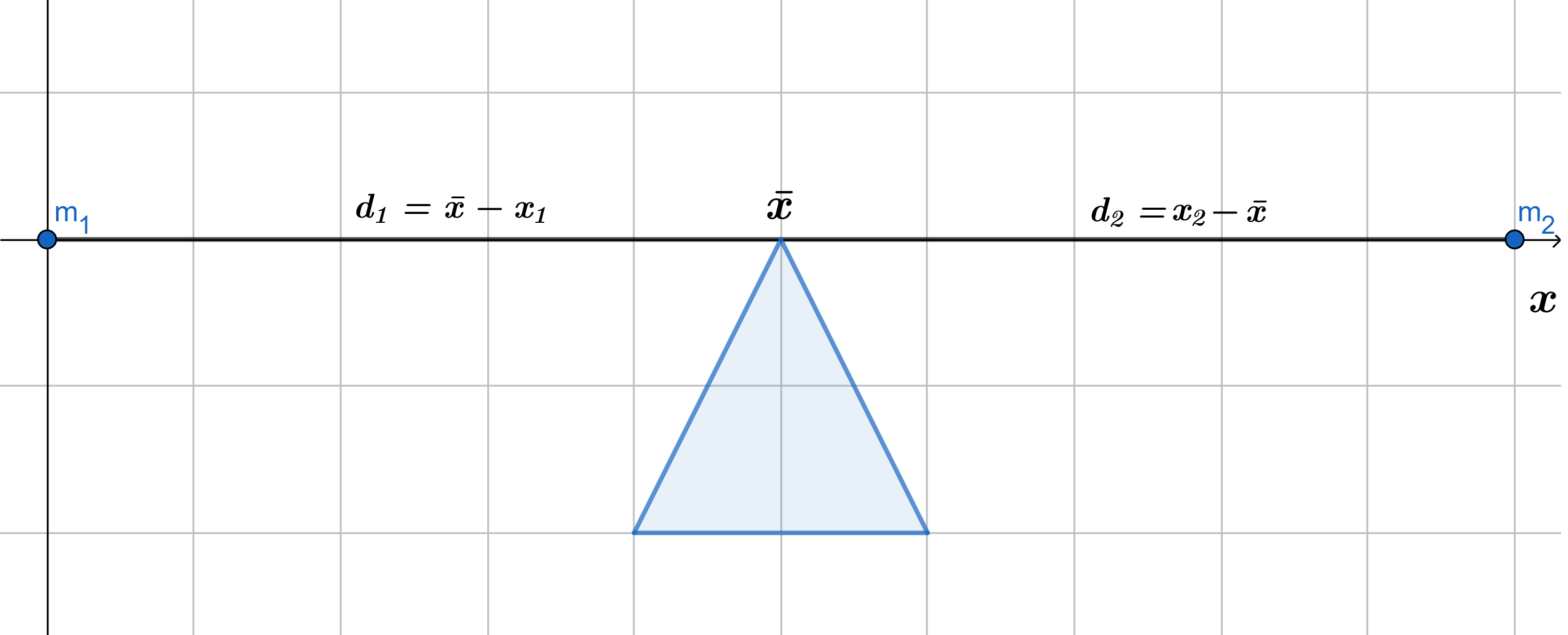
Comencemos con el caso de una varilla balanceada en un punto sobre el eje $x$ y en sus extremos una masa $m_{1}$ en $x_{1}$ y $m_{2}$ en $x_{2}$ como se muestra en la figura $(1)$. Sea $\bar{x}$ el centro de masa, la varilla se balanceara si:
$$m_{1}d_{1}=m_{2}d_{2}$$
Donde $d_{1}=\bar{x}-x_{1}$ y $d_{2}=x_{2}-\bar{x}$, sustituyendo esto en la ecuación anterior, tenemos que:
$$m_{1}(\bar{x}-x_{1})=m_{2}(x_{2}-\bar{x})$$
$$\Rightarrow m_{1}\bar{x}-m_{1}x_{1}=m_{2}x_{2}-m_{2}\bar{x}$$
$$\Rightarrow \bar{x}=\frac{m_{1}x_{1}+m_{2}x_{2}}{m_{1}+m_{2}}$$
Por lo que, podemos calcular el centro de masa $\bar{x}$ del sistema con la relación anterior.
Se define a $m_{i}x_{i}$ el momento de la masa $m_{i}$, en este caso, tenemos dos momentos $m_{1}$ y $m_{2}$ con respecto al origen.
En general, si tenemos un sistema de $n$ partículas con sus respectivas masas $m_{1},\space m_{2}, \space …., \space m_{n}$ respectivamente localizadas en los puntos $x_{1},\space x_{2}, \space …., \space x_{n}$ sobre el eje $x$ y análogamente al estudio anterior, se puede demostrar que el centro de masa se puede calcular como:
$$\bar{x}=\frac{\sum_{i=1}^{n}m_{i}x_{i}}{\sum_{i=1}^{n}m_{i}}=\frac{M}{m}$$
Donde $m$ es la suma de las $n$ masas y $M$ es la suma de los $n$ momentos.
Centro de masas y momentos (bidimensional)
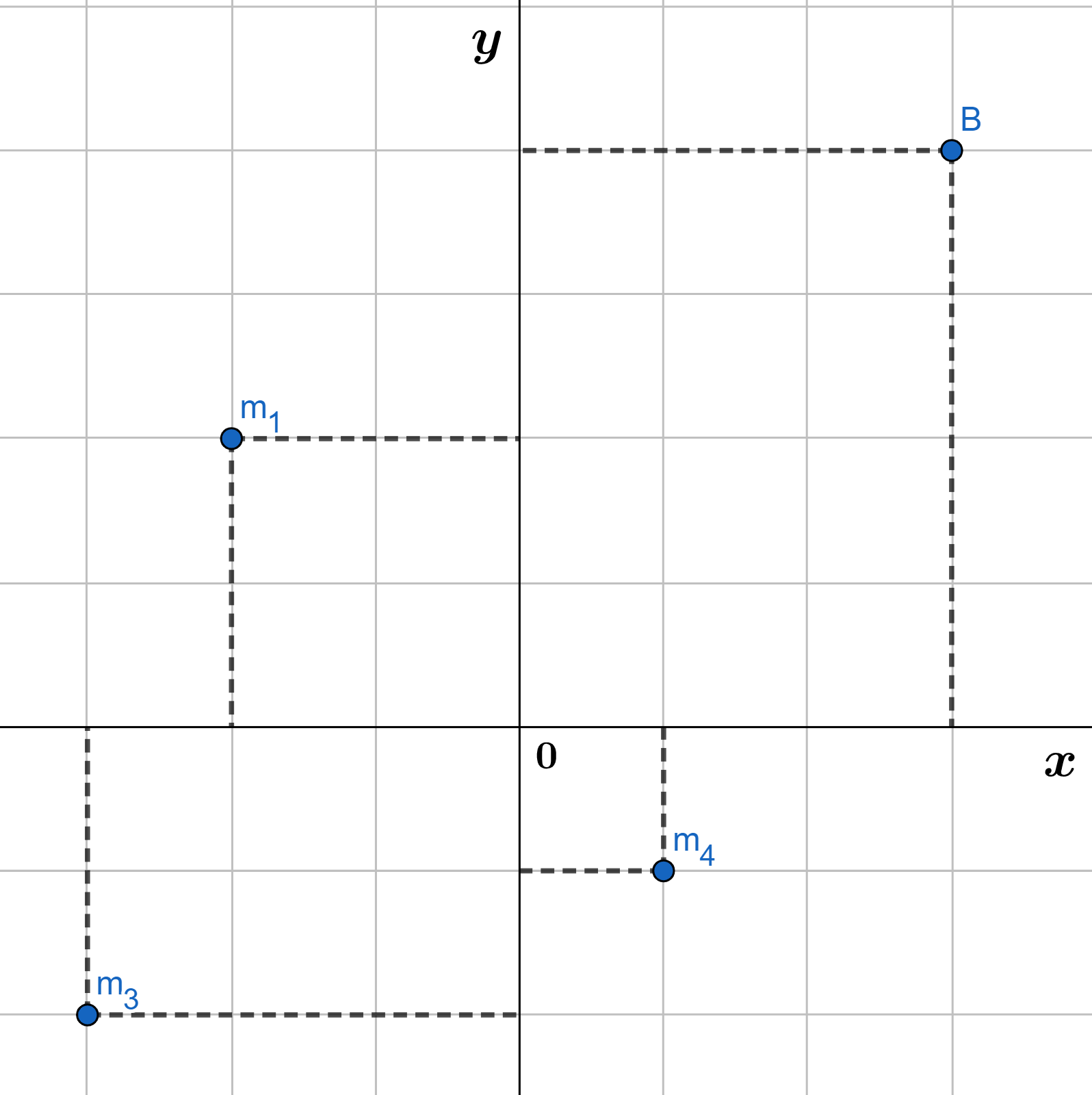
Consideremos ahora un sistema de $n$ partículas con masas $m_{1},\space m_{2}, \space …., \space m_{n}$ localizadas en los puntos $(x_{1},\space y_{1}),\space (x_{2},\space y_{2}), \space …., \space (x_{n},\space y_{n})$ en el plano $xy$ como se muestra en la figura $(2)$.
Análogamente al caso unidimensional, se define el momento del sistema respecto del eje $y$ como:
$$M_{y}=\sum_{i=1}^{n}m_{i}x_{i} \tag{1}$$
Y el momento del sistema respecto del eje $x$ como:
$$M_{x}=\sum_{i=1}^{n}m_{i}y_{i} \tag{2}$$
Por lo que el centro de masa $(\bar{x}, \bar{y})$ está dado como:
$$\bar{x}=\frac{M_{y}}{m} \space \space \space \space \space \space \bar{y}=\frac{M_{x}}{m}$$
Consideremos una placa con densidad uniforme $\rho$, se desea localizar su centro de masa, para esto, supongamos que esta región está en el intervalo $[a, b]$, dividimos este intervalo en $n$ subintervalos con puntos extremos $x_{0}, \space x_{1}, \space…., \space x_{n}$ e igual amplitud $\Delta x$. Sea $\bar{x_{i}}$ el punto medio del intervalo $[x_{i-1}, \space x_{i}]$, por lo que $\bar{x_{i}}=(x_{i-1}+x_{i})/2$, así, tendremos $n$ polígonos o $R_{i}$ rectángulos, aproximando a la placa como se muestra en la figura $(3)$.
El área del i-esimo rectángulo es:
$$A_{i}=f(\bar{x_{i}}) \Delta x_{i}$$
Como estamos en el caso bidimensional, recordemos que la densidad es una densidad superficial dada como:
$$\rho = \frac{M}{A}$$
Por lo que, para la masa:
$$M=\rho f(\bar{x_{i}}) \Delta x_{i}$$
El momento del rectángulo $R_{i}$ respecto del eje $y$ es el producto de su masa y la distancia del centroide del i-esimo rectángulo $R_{i}$ que es $C_{i}(\bar{x_{i}}, \frac{1}{2}f(\bar{x_{i}}))$ como se muestra en la figura $(3)$, por la definición de $M_{y}$ $(1)$, se tiene que:
$$M_{y}(R_{i})=(\rho f(\bar{x_{i}}) \Delta x_{i})\bar{x_{i}}$$
Al sumar estos momentos y tender $n \to \infty$ tenemos que:
$$M_{y}=\lim_{n \to \infty}\sum_{i=1}^{n}(\rho f(\bar{x_{i}}) \Delta x_{i})\bar{x_{i}}=\rho \int_{a}^{b}xf(x)dx $$
Del modo similar, el momento del rectángulo $R_{i}$ respecto del eje $x$ está dado como el producto de su masa por la distancia $C_{i} (\bar{x_{i}}, \frac{1}{2}f(\bar{x_{i}})) $ al eje $x$, por la definición de $M_{x}$ $(2)$, se tiene que:
$$M_{x}(R_{i})=(\rho f(\bar{x_{i}}) \Delta x_{i})\frac{1}{2}f(\bar{x_{i}})=\rho \frac{1}{2}[f(\bar{x_{i}}]^{2} \Delta x$$
Tomando el límite:
$$M_{x}=\lim_{n \to \infty}\sum_{i=1}^{n}\rho \frac{1}{2}[f(\bar{x_{i}}]^{2} \Delta x= \int_{a}^{b} \rho \frac{1}{2}[f(\bar{x_{i}}]^{2} dx $$
El centro de masa de la placa se define análogamente al sistema de $n$ partículas como:
$$\bar{x}=\frac{M_{y}}{m}$$
$$\bar{y}=\frac{M_{x}}{m}$$
Pero la masa de la placa es el producto de su densidad y su área, la cual podemos calcularla por medio de una integral:
$$m=\rho A=\rho \int_{a}^{b}f(x)dx$$
Por tanto, para calcular el centroide $(\bar{x},\bar{y})$ de esta placa se tiene que:
$$\bar{x}=\frac{M_{y}}{m}=\frac{\rho \int_{a}^{b}xf(x)dx}{\rho \int_{a}^{b}f(x)dx}=\frac{\int_{a}^{b}xf(x)dx}{\int_{a}^{b}f(x)dx}=\frac{1}{A}\int_{a}^{b}xf(x)dx \tag{3}$$
$$\bar{y}=\frac{M_{x}}{m}=\frac{\rho \int_{a}^{b}\frac{1}{2}[f(x)]^{2}dx}{\rho \int_{a}^{b}f(x)dx}=\frac{\int_{a}^{b}\frac{1}{2}[f(x)]^{2}dx}{\int_{a}^{b}f(x)dx}=\frac{1}{A}\int_{a}^{b}\frac{1}{2}[f(x)]^{2}dx \tag{4}$$
Si la región se encuentra entre dos curvas $y=f(x)$ y $y=g(x)$ donde $f(x)\geq g(x)$ podemos utilizar el mismo método anterior para encontrar el centroide $(\bar{x},\bar{y})$ como:
$$\bar{x}=\frac{\int_{a}^{b}x[f(x)-g(x)]dx}{\int_{a}^{b}(f(x)-g(x))dx}$$
$$\bar{y}=\frac{\int_{a}^{b}[f^{2}(x)-g^{2}(x)]dx}{2\int_{a}^{b}(f(x)-g(x))dx}$$
Veamos los siguientes ejemplos.
Ejemplos
- Suponga que se colocan tres masas puntuales en el plano $xy$ de la siguiente manera: $m_{1}=2 kg$ en la coordenada $(-1,3)$, $m_{2}= 6 kg$ en la coordenada $(1,1)$ y $m_{3}=4kg$ en la coordenada $(2,-2)$. Encuentre el centro de masa del sistema.
Calculamos la masa total como:
$$m=\sum_{i=1}^{3}m_{i}=2+6+4=12 kg$$
Ahora, encontrando los momentos respectivos en el eje $x$ y $y$:
$$M_{y}=\sum_{i=1}^{3}m_{i}x_{i}=-2+6+8=12$$
$$M_{x}=\sum_{i=1}^{3}m_{i}y_{i}=6+6-8=4$$
Calculando el centro de masas:
$$\bar{x}=\frac{M_{y}}{m}=\frac{12}{12}=1$$
$$\bar{y}=\frac{M_{x}}{m}=\frac{4}{12}=\frac{1}{3}$$
Por lo que el centro de masas de este sistema es:
$$(\bar{x},\bar{y})=(1, \frac{1}{3})$$
- Encuentre el centroide de la región acotada por las curvas $y=\cos(x)$,$y=0$, $x=0$ y $x=\pi/2$.
El área de la región es:
$$A=\int_{0}^{\pi /2}\cos(x)dx=\sin(x) \bigg|_{0}^{\pi /2}=1$$
Así, calculando el centroide se tiene que, para $\bar{x}$ $(3)$:
$$\bar{x}=\frac{1}{A}\int_{0}^{\pi /2}xf(x)dx=\int_{0}^{\pi /2}x\cos(x)dx=x\sin(x)\bigg|_{0}^{\pi /2}-\int_{0}^{\pi /2}\sin(x)dx$$
$$=\frac{\pi}{2}-1$$
Para $\bar{y}$ $(4)$:
$$\bar{y}=\frac{1}{A}\int_{0}^{\pi /2}\frac{1}{2}(f(x))^{2}dx=\frac{1}{2}\int_{0}^{\pi /2}\cos^{2}(x)dx$$
$$=\frac{1}{4}\int_{0}^{\pi /2}(1+\cos(2x))dx=\frac{1}{4}\left [ x+\frac{1}{2}\sin(2x) \right ]\bigg|_{0}^{\pi /2}=\frac{\pi}{8}$$
Por tanto, el centroide es: $$(\bar{x},\bar{y})=(\frac{\pi}{2}-1,\frac{\pi}{8})$$
Tarea moral
Los siguientes ejercicios no son para evaluación, pero son ejercicios para que practiques lo aprendido que te ayudaran en el desarrollo del entendimiento del tema, por lo que te invitamos a resolver los siguientes ejercicios propuestos relacionados con el tema visto.
A continuación hay algunos ejercicios para que practiques los conceptos vistos en esta entrada. Te será de mucha utilidad intentarlos para entender más la teoría vista.
- Encuentre los momentos del centro de masas cuyas masas son 3, 4 y 8 con coordenadas $(-1, 1)$, $(2, -1)$ y $(3, 2)$ respectivamente.
- Demuestre que el centro de masas de una varilla o de una franja recta y delgada de densidad constante se encuentra en su punto medio.
- Una varilla de longitud de 10cm. aumenta su grosor de izquierda a derecha en función de $f(x)=1+(x/10) kg/m$. Determinar el centro de masas de la varilla.
- Encuentre el centro de masas de una placa semicircular de radio $r$.
- Encuentre el centroide de la región acotada por la recta $y=x$ y la parábola $y=x^{2}$.
Más adelante…
En esta sección vimos como calcular el centro de masas y el momento de un sistema, en la siguiente sección veremos otra la aplicación de la integral en el área de la física, y es la aplicación de la integración al concepto de trabajo.
Entradas relacionadas
- Ir a Cálculo Diferencial e Integral II.
- Entrada anterior del curso: Cálculo Diferencial e Integral II: Teorema de Pappus-Guldinus – El blog de Leo (nekomath.com)
- Siguiente entrada del curso: Cálculo Diferencia e Integral II: Aplicación de la integración al concepto de trabajo – El blog de Leo (nekomath.com)