$\textit{MATERIAL EN REVISIÓN}$
Introducción
En esta entrada conoceremos dos lemas más previos a la demostración del teorema de Stone-Weierstrass. Las hipótesis a usar serán las mismas que se mencionaron en la entrada anterior: $K$ es un espacio métrico compacto, $A \subset \mathcal{C}^0(K, \mathbb{R}),$ es decir, $A$ es un conjunto de funciones continuas que transforma valores en $K$ en valores reales. Supondremos también que $A$ satisface las propiedades:
a) Para cada $\lambda, \mu \, \in \mathbb{R}$ y $f,g \in A$ se cumple que $$\lambda f + \mu g \, \in A.$$ Esto es, $A$ es cerrado bajo combinaciones lineales.
b) Para cada $f,g \in A$ se cumple que $$f \cdot g \, \in A.$$ Esto es, $A$ es cerrado bajo producto de funciones.
c) $1 \in A,$ donde $1$ es la función constante que para cada $x \in K$ asigna el valor $1.$
d) Para cualesquiera $x_1, x_2 \in K$ tales que $x_1 \neq x_2$ existe una función $\varphi \in A$ tal que $\varphi (x_1) \neq \varphi(x_2).$
Entonces se satisface el siguiente:
Lema 3. Si $\varphi \in \overline{A}$ entonces $|\varphi| \in \overline{A}.$
Demostración:
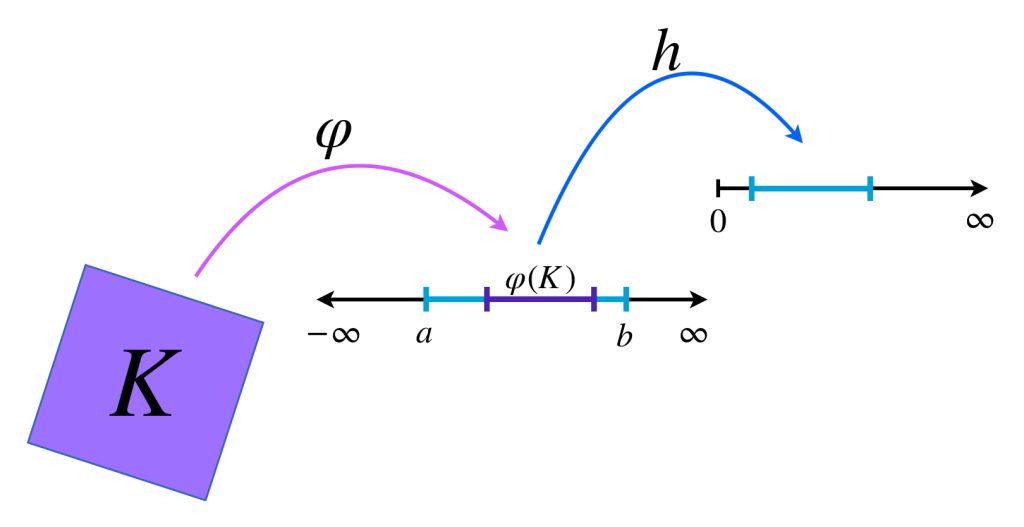
Sabemos que $\varphi: K \to \mathbb{R}$ es continua. Dado que $K$ es compacto, la imagen $\varphi(K)$ es compacta en $\mathbb{R}$, y por tanto es acotada, así $\varphi (K) \subset [a,b]$ para algún $a,b \in \mathbb{R}.$ Como la función valor absoluto restringida en $[a,b],$ que denotamos con $h: [a,b] \to \mathbb{R} \,$ tal que $\forall \, y \in \mathbb{R}, h(y) = |y|$ también es continua en su dominio, se sigue que la composición
$$h \circ \varphi (x)= |\varphi(x)|$$
es continua en $K$.
El siguiente diagrama muestra el comportamiento de las funciones.
Por lo visto en la entrada tal podemos aproximar la función $h:[a,b] \to \mathbb{R}$ con polinomios de Bernstein. Sea
$$B_n(h,y)= a_0 + a_1y+…+a_ny^n$$
el polinomio de Bernstein de grado a lo más $n$ de $h$ con $y \in [a,b].$ Entonces
$$\underset{n \to \infty}{lim} \, \norm{B_n(h,y) \, – \, h}_{\infty} = 0.$$
Si $x \in K,$ $\, \varphi(x) \in [a,b].$ Evaluando el polinomio en $\varphi(x)$ tenemos:
$$B_n(h,\varphi(x))= a_0 + a_1\varphi(x)+…+a_n\varphi(x)^n.$$
De modo que la sucesión de polinomios $(B_n(h,\varphi(x)))_{n \in \mathbb{N}} \,$ converge a $h \circ \varphi = |\varphi|$ en $\mathcal{C}^0(K, \mathbb{R}).$
Veamos que cada sumando del polinomio está en $\overline{A}.$ Para ello usaremos los resultados del lema 2 visto en link.
La función constante $1 \in \overline{A},$ como $a_0 \in \mathbb{R}$ se sigue que el producto $1 \cdot a_0 = a_0 \in \overline{A}.$
Como $\varphi \in A \subset \overline{A}$ y $a_1 \in \mathbb{R}$ se sigue que el producto $a_1 \varphi \in \overline{A}.$
Como $\varphi \in A \subset \overline{A}$ entonces el producto $\varphi \cdot \varphi = \varphi ^2 \in \overline{A}.$ Como $a_2 \in \mathbb{R}$ se sigue que también $a_2 \varphi ^2 \in \overline{A}.$
.
.
.
Como $\varphi^{n-1} \in A \subset \overline{A}$ entonces el producto $\varphi^{n-1} \cdot \varphi = \varphi ^n \in \overline{A}.$ Como $a_n \in \mathbb{R}$ se sigue que el producto $a_n \varphi ^n \in \overline{A}.$
Ya que cada sumando está en $\overline{A}$ concluimos que para cada $n \in \mathbb{N}, \, B_n(h,\varphi(x)) \in \overline{A}.$ Por lo tanto $|\varphi| \in \overline{A}.$
Para finalizar esta sección veamos otro resultado.
Lema 4. Sean $\varphi, \gamma \in \overline{A}.$ Entonces las funciones
$$\text{máx}\{\varphi, \gamma\}(x):= \text{máx}\{\varphi(x), \gamma(x)\} \, \text{ y }$$
$$\text{mín}\{\varphi, \gamma\}(x):= \text{mín}\{\varphi(x), \gamma(x)\}$$
también están en $\overline{A}.$
Demostración:
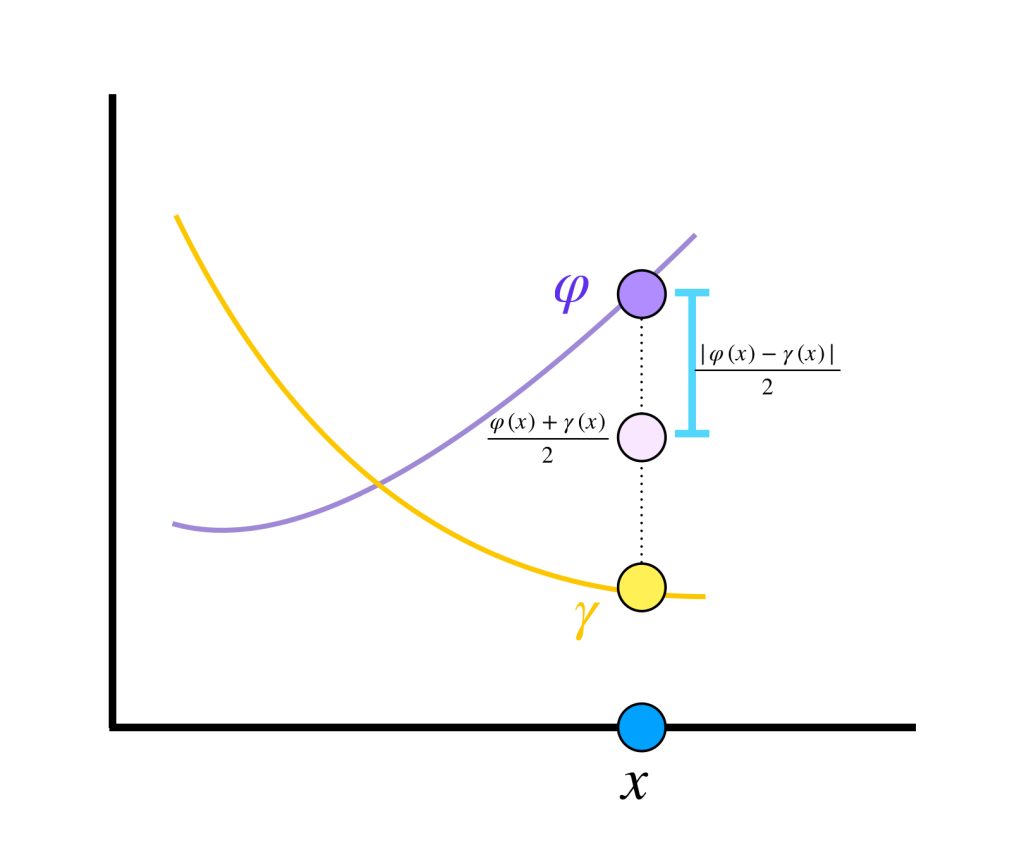
Probemos que $\text{máx}\{\varphi, \gamma\}(x) \in \overline{A}.$ Nota que
$$\text{máx}\{\varphi(x), \gamma(x)\}=\dfrac{\varphi(x)+\gamma(x)+|\varphi(x) \, – \, \gamma(x)|}{2},$$
pues en el caso en que $\varphi(x) \geq \gamma(x)$
\begin{align*}
\dfrac{\varphi(x)+\gamma(x)+|\varphi(x) \, – \, \gamma(x)|}{2} &= \dfrac{\varphi(x)+\gamma(x)+(\varphi(x) \, – \, \gamma(x))}{2}\\
&= \dfrac{2\varphi(x)}{2}\\
&=\varphi(x)
\end{align*}
Por otro lado, si $\gamma(x) \geq \varphi(x)$
\begin{align*}
\dfrac{\varphi(x)+\gamma(x)+|\varphi(x) \, – \, \gamma(x)|}{2} &= \dfrac{\varphi(x)+\gamma(x)+(\gamma(x) \, – \, \varphi(x))}{2}\\
&= \dfrac{2\gamma(x)}{2}\\
&=\gamma(x)
\end{align*}
Ya que $\dfrac{\varphi(x)+\gamma(x)+|\varphi(x) \, – \, \gamma(x)|}{2}$ puede verse como combinación lineal de funciones en $\overline{A}$ (por lo visto en lema 2 y lema 3) se sigue que
$\dfrac{\varphi(x)+\gamma(x)+|\varphi(x) \, – \, \gamma(x)|}{2} = \text{máx}\{\varphi(x), \gamma(x)\} \, \in \overline{A}.$
Análogamente se puede probar que se satisface la igualdad
$\text{mín}\{\varphi(x), \gamma(x)\} = \dfrac{\varphi(x)+\gamma(x)-|\varphi(x) \, – \, \gamma(x)|}{2}$
Y así la función $\, \text{mín}\{\varphi(x), \gamma(x)\} \, \in \overline{A}.$ La prueba de este hecho se dejará como ejercicio.
Más adelante…
Terminaremos con la demostración del teorema prometido. Por lo pronto sugerimos algunos ejercicios.
Tarea moral
- Demuestra que $\text{mín}\{\varphi(x), \gamma(x)\} = \dfrac{\varphi(x)+\gamma(x)-|\varphi(x) \, – \, \gamma(x)|}{2}.$
- Identifica bajo qué condiciones las siguientes familias de funciones satisfacen las hipótesis del teorema de Stone-Weierstrass:
a) Las poligonales.
b) Las funciones infinitamente diferenciables en $\mathbb{R}.$
c) Las funciones Lipschitz continuas.