Introducción
El contenido de esta sección se basa predominantemente en el libro
Wheeden, R.L., Zygmund, A., Measure and Integral. An Introduccion to Real Analysis. (2da ed.). New York: Marcel Dekker, 2015, págs 30-34.
Continuaremos viendo condiciones bajo las cuales sea posible afirmar la existencia de la integral $\int_{a}^{b}f \, d\alpha.$ Comencemos con la siguiente:
Proposición: Sean $f, \alpha:[a,b] \to \mathbb{R}.$ Si $\, \int_{a}^{b}\textcolor{RoyalBlue}{f} \, d\textcolor{magenta}{\alpha} \,$ existe, entonces también $\, \int_{a}^{b}\textcolor{magenta}{\alpha} \, d\textcolor{RoyalBlue}{f} \,$ existe y además
\begin{align}
\int_{a}^{b}f \, d\alpha = [f(b)\alpha(b) \, – \, f(a)\alpha(a)] \, – \int_{a}^{b} \alpha \, df.
\end{align}
Demostración:
Considera $P= \{x_0=a,…,x_n=b\}$ una partición de $[a,b] \,$ y sean $\xi_i \in [x_{i-1},x_i], \, i=1,…,n.$ Entonces se siguen las siguientes igualdades:
\begin{align*}
S(P,f,\alpha)&= \sum_{i=1}^{n}f(\xi_i)(\alpha(x_i) \, – \, \alpha(x_{i-1}))\\
&= \sum_{i=1}^{n}f(\xi_i)\alpha(x_i) \, – \, \sum_{i=1}^{n}f(\xi_i)\alpha(x_{i-1})\\
&= \sum_{i=1}^{n}f(\xi_i)\alpha(x_i) \, – \, \sum_{i=0}^{n-1}f(\xi_{i+1})\alpha(x_i)\\
&= \sum_{i=1}^{n-1}f(\xi_i)\alpha(x_i)+ f(\xi_n)\alpha(x_n)\, – \, \sum_{i=1}^{n-1}f(\xi_{i+1})\alpha(x_i) \, – \, f(\xi_1)\alpha(x_0)\\
&=- \sum_{i=1}^{n-1}\alpha(x_i)(f(\xi_{i+1}) \, – \, f(\xi_i))) + f(\xi_n)\alpha(b) \, – \, f(\xi_1)\alpha(a).
\end{align*}
Nota que el lado derecho de la igualdad coincide con
$$[f(b)\alpha(b) \, – \, f(a)\alpha(a)] \, – \, \textcolor{blue}{T_P}$$
donde
$$\textcolor{blue}{T_P}= \sum_{i=1}^{n-1}\alpha(x_i)(f(\xi_{i+1}) \, – \, f(\xi_i))+\alpha(a)(f(\xi_1) \, – \, f(a))+\alpha(b)(f(b) \, – \, f(\xi_n)). $$
Por lo tanto
\begin{align}
S(P,f,\alpha) = [f(b)\alpha(b) \, – \, f(a)\alpha(a)] \, – \, \textcolor{blue}{T_P}.
\end{align}
Observa que $\textcolor{blue}{T_P}$ es una suma de Riemann-Stieltjes para $\textcolor{blue}{\int_{a}^{b} \alpha \, df.}$ Tomando el límite cuando $|P| \to 0$ en (2) vemos que $\int_{a}^{b}f \, d\alpha$ existe si y solo si $\int_{a}^{b} \alpha \, df$ existe y que
\begin{align*}
\int_{a}^{b}f \, d\alpha = [f(b)\alpha(b) \, – \, f(a)\alpha(a)] \, – \int_{a}^{b} \alpha \, df,
\end{align*}
que es lo que queríamos demostrar.
Ya que el valor de las sumas de Riemann-Stieltjes depende de los valores $\xi_i$ elegidos, cuando la función $f$ es acotada, podemos delimitar el valor de $f(\xi_i)$ y, por tanto, acotar las sumas como muestra la siguiente:
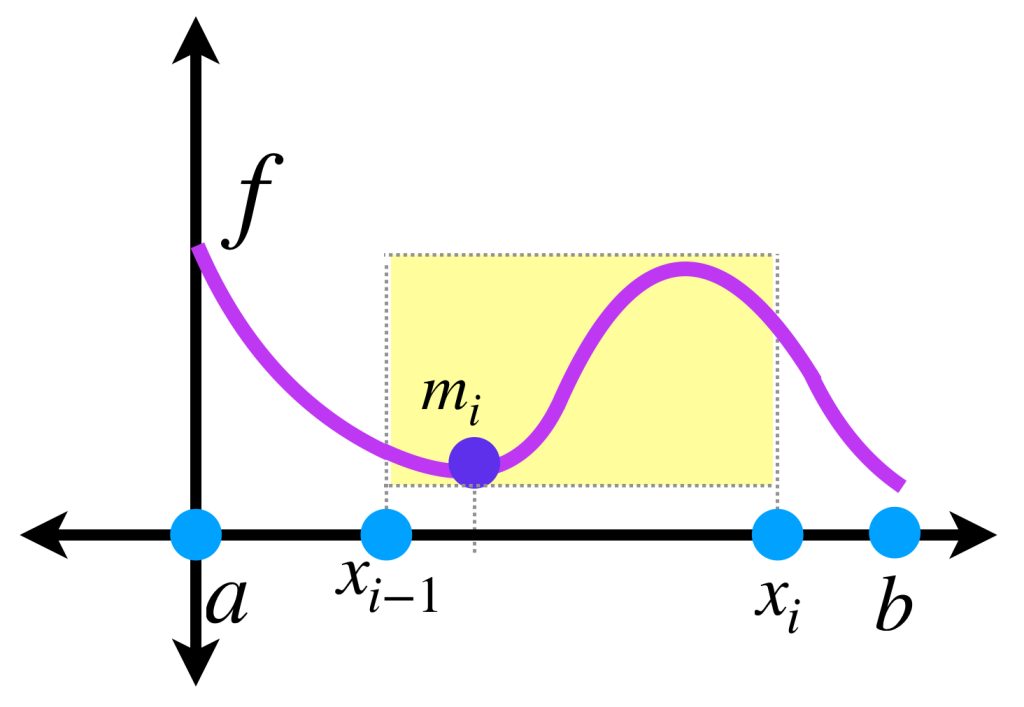
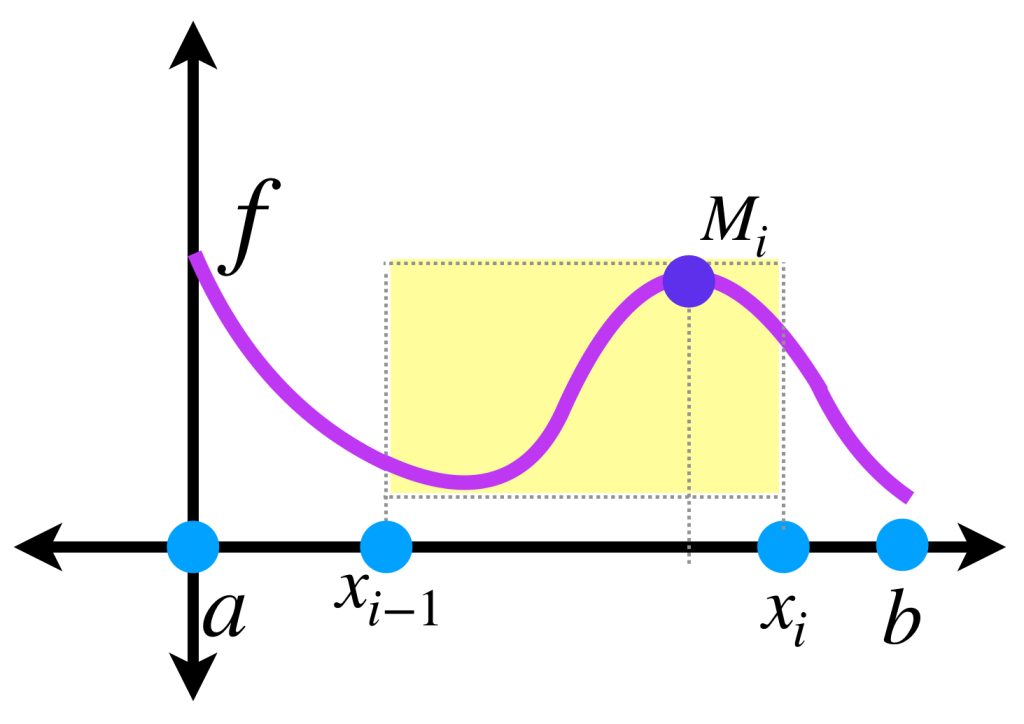
Definición: Suma inferior y suma superior de Riemann-Stieltjes. Sea $f$ acotada, $\alpha$ una función monótona creciente en $[a,b]$ y $P=\{x_0=a,…,x_n=b\}.$ Definimos los términos:
\begin{align*}
m_i= \underset{x \, \in \, [x_{i-1}, x_i]}{\text{ínf}} \, f(x)
\end{align*}
\begin{align*}
M_i= \underset{x \, \in \, [x_{i-1}, x_i]}{\text{sup}} \, f(x)
\end{align*}
Las siguientes sumas
\begin{align}
\underline{S}_P = \sum_{i=1}^{n} m_i \, (\alpha(x_i) \, – \, \alpha(x_{i-1}))\\
\nonumber \\
\overline{S}_P = \sum_{i=1}^{n} M_i \, (\alpha(x_i) \, – \, \alpha(x_{i-1}))
\end{align}
reciben el nombre de suma inferior y suma superior de Riemann-Stieltjes, respectivamente.
Dado que $-\infty < m_i \leq M_i < \infty \,$ y $\, (\alpha(x_i) \, – \, \alpha(x_{i-1}))\geq 0, \,$ (pues $\alpha$ es creciente), podemos ver que
$$\underline{S}_P \leq S(P,f,\alpha) \leq \overline{S}_P.$$
Esta forma de definir sumas permite conocer el comportamiento de la función, como sugiere el siguiente:
Lema: Sea $f:[a,b] \to \mathbb{R}$ acotada y $\alpha:[a,b] \to \mathbb{R}$ creciente. Se cumplen:
a) Si $Q$ es un refinamiento de $P \in \mathcal{P}_{[a,b]},$ entonces
$$\underline{S}_P \leq \underline{S}_Q \leq \overline{S}_Q \leq \overline{S}_P.$$
b) Si $P_1$ y $P_2$ son dos particiones, entonces
$$\underline{S}_{P_1} \leq \overline{S}_{P_2},$$
es decir, cualquier suma inferior de Riemann-Stieltjes es menor igual que cualquier suma superior de Riemann-Stieltjes.
Demostración:
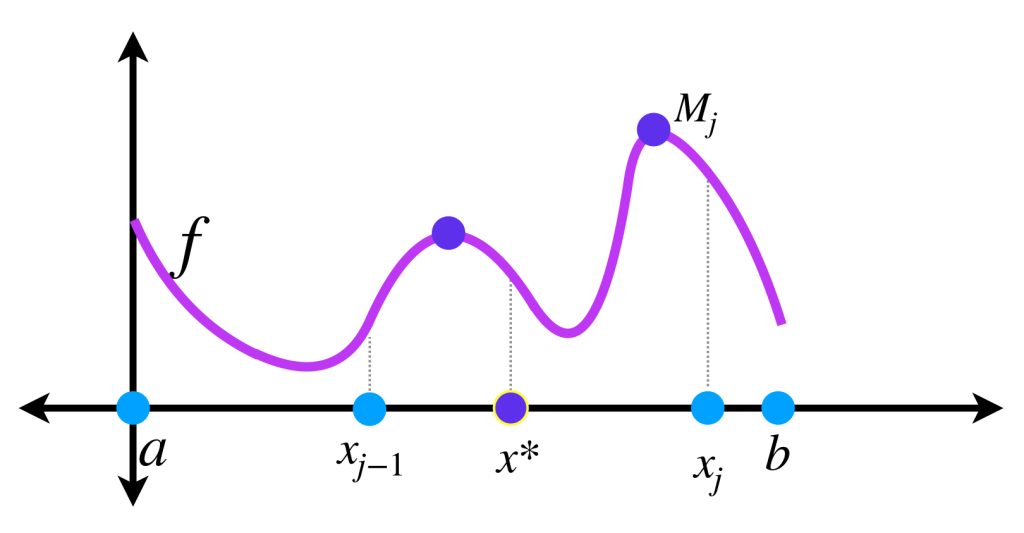
a) Vamos a demostrar que $\overline{S}_Q \leq \overline{S}_P.$ El argumento para las sumas inferiores es análogo y lo dejaremos como ejercicio.
Sea $P=\{x_0=a,…,x_n=b\} \,$ y $\, P \subset Q.$ Para fines prácticos supongamos que $Q$ tiene apenas un punto más que $P.$ Sea $x^*$ ese punto.
Entonces $x^* \in [x_{j-1},x_j]$ para algún $j \in \{1,…,n\}$
entonces
\begin{align*}
\underset{[x_{j-1},x^*]}{sup} \, f(x) &\leq M_j \, \text{ y} \\
\\
\underset{[x^*,x_j]}{sup} \, f(x) &\leq M_j
\end{align*}
en consecuencia
$$\underset{[x_{j-1},x^*]}{sup} \, f(x) \, \, (\alpha(x^*) \, – \, \alpha(x_{i-1})) + \underset{[x^*,x_j]}{sup} \, f(x) \, \, (\alpha(x_j) \, – \, \alpha(x^*)) \leq M_j (\alpha(x_j) \, – \, \alpha(x_{j-1})). $$
Este razonamiento se puede repetir añadiendo uno a uno cada punto de $\, Q \setminus P \,$ hasta obtener $Q.$ Finalmente,
$$\overline{S}_Q \leq \overline{S}_P.$$
b) Nota que $P_1 \cup P_2$ es un refinamiento tanto de $P_1$ como de $P_2.$ Aplicando a) obtenemos:
$$\underline{S}_{P_1} \leq \underline{S}_{P_1 \cup P_2} \leq \overline{S}_{P_1 \cup P_2} \leq \overline{S}_{P_2}$$
con lo cual terminamos la prueba.
El siguiente enunciado muestra condiciones suficientes para la existencia de la integral de Riemann-Stieltjes.
Proposición: Sea $f:[a,b] \to \mathbb{R}$ continua y $\alpha:[a,b] \to \mathbb{R}$ de variación acotada en $[a,b],$ entonces $\int_{a}^{b}$ existe. Más aún
$$\left|\int_{a}^{b}f \, d\alpha \right|\leq \left(\underset{x \in [a,b]}{sup}|f(x)|\right) V[\alpha;a,b]. $$
Demostración:
Para demostrar la existencia recordemos que el teorema de Jordan visto en la entrada Funciones de variación acotada dice que $\alpha, \, $ al ser de variación acotada, puede expresarse como $\alpha = \alpha_1 \, – \, \alpha_2\, $ con $\alpha_1$ y $\alpha_2$ funciones crecientes acotadas en $[a,b].$ Si probamos que existe tanto $\int_{a}^{b}f \, d\alpha_1$ como $\int_{a}^{b}f \, d\alpha_2, \,$ entonces, por lo visto en la entrada anterior también existe la integral buscada pues
\begin{align}
\nonumber \int_{a}^{b}f \, d\alpha_1 \, – \int_{a}^{b}f \, d\alpha_2 &= \int_{a}^{b}f \, d\alpha_1 \, + \int_{a}^{b}f \, d(-\alpha_2) \\
\nonumber&=\int_{a}^{b}f \, d(\alpha_1- \alpha_2)\\
&=\int_{a}^{b}f \, d\alpha.
\end{align}
Sin pérdida de generalidad, probemos que $\int_{a}^{b}f \, d\alpha_1\, $ existe. Sea $P=\{x_1=a,…,x_n=b\}.$ De acuerdo con la proposición que acabamos de ver
$$\underline{S}_P \leq S(P,f, \alpha_1) \leq \overline{S}_P.$$
A continuación vamos a demostrar que $\underset{|P| \to 0}{lim}\, \underline{S}_P \,$ y $\, \underset{|P| \to 0}{lim}\, \overline{S}_P$ existen y son iguales. La condición es evidente si $\alpha_1$ es constante así que supongamos que no lo es.
Sea $\varepsilon>0.$ Ya que $f$ es uniformemente continua en $[a,b]$ sabemos que existe $\delta>0$ tal que si $|P|< \delta,$ entonces
\begin{align*}
\textcolor{PineGreen}{M_i-m_i < \frac{\varepsilon}{\alpha_1(b) \, – \, \alpha_1(a)}}.
\end{align*}
Nota que $\alpha_1(b) \, – \, \alpha_1(a)$ es distinto de cero, pues $\alpha_1$ es monótona no constante.
Si $|P|< \delta \,$ se sigue:
\begin{align*}
0 \leq \overline{S}_P \, – \, \underline{S}_P &= \sum_{i=1}^{n}\textcolor{PineGreen}{(M_i\, – \, m_i)}(\alpha_1(x_i) \, – \, \alpha_1(x_{i-1}))\\
&< \sum_{i=1}^{n}\textcolor{PineGreen}{\left( \frac{\varepsilon}{\alpha_1(b) \, – \, \alpha_1(a)} \right)}(\alpha_1(x_i) \, – \, \alpha_1(x_{i-1}))\\
&= \frac{\varepsilon}{\alpha_1(b) \, – \, \alpha_1(a)} \sum_{i=1}^{n} (\alpha_1(x_i) \, – \, \alpha_1(x_{i-1}))\\
&=\left( \frac{\varepsilon}{\cancel{\alpha_1(b) \, – \, \alpha_1(a)}} \right) \cancel{(\alpha_1(b) \, – \, \alpha_1(a))}\\
&= \varepsilon.
\end{align*}
Por lo tanto
\begin{align}
\underset{|P| \to 0}{lim} \, (\overline{S}_P \, – \, \underline{S}_P) = 0.
\end{align}
A continuación probaremos que existe $\underset{|P| \to 0}{lim} \, \overline{S}_P$ en $\mathbb{R}.$ Si suponemos que no existe entonces, por el criterio de Cauchy visto en la entrada anterior, existen $\varepsilon >0$ y $(P’_k)_{k \in \mathbb{N}}$ y $(P ^{\prime \prime} _k)_{k \in \mathbb{N}} \,$ sucesiones de particiones cuyas normas tienden a cero tales que
$$\textcolor{purple}{\overline{S}_{P’_k} \, – \, \overline{S}_{P^{\prime \prime}_k} > \varepsilon}.$$
Por (6) sabemos que para $k$ suficientemente grande
\begin{align*}
&& \overline{S}_{P’_k} \, – \, \underline{S}_{P’_k} &< \frac{\varepsilon}{2} \\
&\Rightarrow& \underline{S}_{P’_k} \, – \, \overline{S}_{P’_k} &>-\frac{\varepsilon}{2} \\
&\Rightarrow& \textcolor{purple}{\overline{S}_{P’_k} \, – \, \overline{S}_{P^{\prime \prime}_k}}+ \underline{S}_{P’_k} \, – \, \overline{S}_{P’_k} &> \textcolor{purple}{\varepsilon}\, -\frac{\varepsilon}{2}\\
&\Rightarrow& \underline{S}_{P’_k} \, – \, \overline{S}_{P^{\prime \prime}_k} &> \frac{\varepsilon}{2}\\
&\Rightarrow& \underline{S}_{P’_k} \, – \, \overline{S}_{P^{\prime \prime}_k} &> 0
\end{align*}
lo que contradice el hecho de que $\underline{S}_{P’} \leq \overline{S}_{P^{\prime \prime}}$ para cualquier $P’$ y $P^{\prime \prime}.$
Por lo tanto $\underset{|P| \to 0}{lim} \, \overline{S}_P$ existe y en consecuencia $\int_{a}^{b}f \, d \alpha_1$ existe. Análogamente, $\int_{a}^{b}f \, d \alpha_2 \,$ existe, por lo tanto $\int_{a}^{b}f \, d \alpha \,$ también existe.
Para terminar la prueba nota que la desigualdad
$$\left|\int_{a}^{b}f \, d\alpha \right|\leq \left(\underset{x \in [a,b]}{sup}|f(x)|\right) V[\alpha;a,b] $$
se sigue de una suma de Riemann-Stieltjes similar y haciendo tender el límite a cero. La prueba de este hecho se dejará como ejercicio.
Finalizaremos esta sección con un teorema conocido, pero ahora en la versión con la integral de Riemann-Stieltjes.
Teorema. Del valor medio para la integral de Riemann-Stieltjes. Sea $f:[a,b] \to \mathbb{R}$ continua y $\alpha:[a,b] \to \mathbb{R}$ acotada y creciente. Entonces existe $\xi \in [a,b]$ tal que
\begin{align}
\int_{a}^{b} f \, d\alpha = f(\xi) \, (\alpha(b)\, – \, \alpha(a)).
\end{align}
Demostración:
Dado que $\alpha$ es creciente, se satisface para cualquier $P \in \mathcal{P}_{[a,b]}$
$$\left(\underset{x \, \in \, [a,b]}{\text{mín}} f(x)\right) (\alpha(b)\, – \, \alpha(a)) \leq S(P,f,\alpha) \leq \left(\underset{x \, \in \, [a,b]}{\text{máx}} f(x)\right)(\alpha(b)\, – \, \alpha(a))$$
El resultado anterior nos permite afirmar que $\int_{a}^{b} f \, d\alpha$ existe, entonces también se cumple
$$\left(\underset{x \, \in \, [a,b]}{\text{mín}} f(x)\right) (\alpha(b)\, – \, \alpha(a)) \leq \int_{a}^{b} f \, d\alpha \leq \left(\underset{x \, \in \, [a,b]}{\text{máx}} f(x)\right) (\alpha(b)\, – \, \alpha(a)),$$
y como $f$ es continua en $[a,b]$ se sigue del teorema del valor intermedio que existe $\xi \in [a,b]$ tal que
$$\int_{a}^{b} f \, d\alpha = f(\xi) \, (\alpha(b)\, – \, \alpha(a)),$$
que es lo que queríamos demostrar.
Así como definimos la integral de Riemann-Stieltjes en intervalos cerrados, también podemos hacerlo en intervalos abiertos $(a,b) \in \mathbb{R}$ de esta forma: Si $[a’,b’] \subset (a,b)$ y existe $\int_{a’}^{b’}f \, d\alpha,$ haciendo $a’ \to a$ y $b’ \to b$ definimos
$$\int_{a}^{b}f \, d\alpha = \underset{a’ \to a \, ; \, b’ \to b}{lim}\int_{a’}^{b’}f \, d\alpha$$
cuando el límite existe. Así mismo
$$\int_{-\infty}^{\infty}f \, d\alpha = \underset{a \to -\infty \, ; \, b \to \infty}{lim}\int_{a}^{b}f \, d\alpha,$$
cuando el límite existe.
Más adelante…
Hasta el momento no es muy evidente la relacion entre la existencia de la integral de Riemann-Stieltjes con los limites de las sumas inferior y superior de Riemann-Stieltjes, pese a que en Cálculo llegan incluso a considerarse equivalentes cuando coinciden. En la próxima entrada veremos bajo qué condiciones el resultado es válido en la integral que estamos estudiando.
Tarea moral
- Sea $f:[a,b] \to \mathbb{R}$ acotada y $\alpha:[a,b] \to \mathbb{R}$ creciente. Sea $Q$ un refinamiento de $P \in \mathcal{P}_{[a,b]}.$ Demuestra que
$$\underline{S}_P \leq \underline{S}_Q.$$ - Demuestra la desigualdad pendiente
$$\left|\int_{a}^{b}f \, d\alpha \right|\leq \left(\underset{x \in [a,b]}{sup}|f(x)|\right) V[\alpha;a,b] $$
donde $f$ es continua y $\alpha$ es de variación acotada. - Sean $f, \alpha:[a,b] \to \mathbb{R}.$ Prueba que se cumplen:
a) Si $\int_{a}^{b}f \, d\alpha$ existe y $\alpha$ no es constante en ningún subintervalo de $[a,b]$ muestra que $f$ es acotada en $[a,b].$
b) Si $\int_{a}^{b}f \, d\alpha$ existe y $\alpha$ es creciente, muestra que para cada $P \in \mathcal{P}_{[a,b]}$ tenemos $\underline{S}_P \leq \int_{a}^{b}f \, d\alpha \leq \overline{S}_P.$