Introducción
Continuando con lo visto en la entrada anterior, en esta entrada presentaremos algunas propiedades fundamentales del valor esperado. Lo primero que veremos será el valor esperado de una constante, que será una propiedad muy básica pero de uso muy frecuente en la teoría que veremos.
Por otro lado, veremos un teorema muy importante desde los puntos de vista teórico y práctico, conocido como la ley del estadístico inconsciente. A grandes rasgos, este teorema hará posible obtener el valor esperado de \(g(X)\), donde \(X\) es una v.a. y \(g\) es una función.
Valor esperado de una función constante
La primera propiedad importante es que el valor esperado de una constante es la constante misma. Esto tiene sentido, pues si una v.a. toma un único valor $a \in \RR$, entonces se espera que su promedio a la larga sea $a$.
Propiedad. Sea $a \in \RR$ y $f_{a}\colon\Omega\to\RR$ la función constante $a$, de tal modo que $f_{a}(\omega) = a$ para cada $\omega \in \Omega$. Entonces se tiene que
\begin{align*} \Esp{f_{a}} &= a. \end{align*}
Abusando un poco de la notación, lo anterior significa que para cualquier valor constante $a \in \RR$ se cumple que $\Esp{a} = a$.
Demostración. Sea $a \in \RR$ y sea $(\Omega, \mathscr{F}, \mathbb{P})$ un espacio de probabilidad. Se define la función constante $a$ $f_{a}\colon\Omega\to\RR$ como sigue: para cada $\omega\in\Omega$, $f_{a}(\omega) = a$. Se sigue inmediatamente que $f_{a}[\Omega] = \{ a \}$, por lo que $f_{a}$ es una v.a. discreta. De este modo,
\begin{align*} \Esp{f_{a}} &= \sum_{x\in f_{a}[\Omega]} x \Prob{f_{a} = x} \\[1em] &= \sum_{x\in\{a\}} x \Prob{f_{a} = x} \\[1em] &= a \Prob{f_{a} = a} \end{align*}
Ahora, como $f_{a}[\Omega] = \{ a \}$, entonces $f_{a}^{-1}[f_{a}[\Omega]] = f_{a}^{-1}[\{a\}]$, por lo que $\Omega = f_{a}^{-1}[\{ a \}]$. En consecuencia, se tiene que $(f_{a} = a) = \Omega$. Así, llegamos a que
\begin{align*} a \Prob{f_{a} = a} &= a \Prob{ \Omega } = a \cdot 1 = a, \end{align*}
por lo que podemos concluir que
\begin{align*} \Esp{f_{a}} &= a, \end{align*}
que es justamente lo que queríamos demostrar.
$\square$
Valor esperado de la transformación de una v.a.
Otra propiedad importante del valor esperado surge cuando queremos calcular el valor esperado de la transformación de una v.a. Para hacerlo, aparentemente necesitaríamos obtener la densidad o la masa de probabilidad de la transformación para luego calcular su valor esperado. Afortunadamente, esto no será necesario.
Si $X\colon\Omega\to\RR$ es una v.a. y $g\colon\RR\to\RR$ es una función tal que $g(X)$ es una v.a., hay que recordar que la distribución de $g(X)$ puede obtenerse en términos de la de $X$, por lo que el comportamiento probabilístico de $g(X)$ puede expresarse en términos del de $X$. Debido a esto, ¡también el valor esperado de $g(X)$ puede obtenerse usando la densidad o la masa de probabilidad de $X$!
La ley del estadístico inconsciente
De acuerdo con la discusión anterior, presentamos un teorema que posibilita el cálculo del valor esperado de una v.a. $g(X)$ conociendo únicamente la densidad de $X$. Este resultado es conocido como la ley del estadístico inconsciente. ¡Advertencia! La teoría con la que contamos hasta el momento hace necesario dividir la demostración en dos casos: uno para v.a.’s discretas y otro para v.a.’s continuas. En particular, la demostración para el caso discreto es clara y puedes centrar tu atención en ella, ya que te puede brindar una intuición firme de lo que pasa también en el caso continuo. Por el contrario, la demostración del caso continuo es un poco más técnica, e incluso requiere el uso de herramientas que quizás no hayas visto hasta ahora. Durante la demostración te comentaremos cuáles son estas herramientas, y las materias posteriores de la carrera en donde posiblemente las veas.
Teorema. Sea $X\colon\Omega\to\RR$ una v.a. y $g\colon\RR\to\RR$ una función Borel-medible.
- Si $X$ es una v.a. discreta, entonces \begin{align*} \Esp{g(X)} &= \sum_{x \in X[\Omega]} g(x) \Prob{X = x}, \end{align*}siempre que esta suma sea absolutamente convergente.
- Si $X$ y $g(X)$ son v.a.’s continuas, entonces \begin{align*} \Esp{g(X)} &= \int_{-\infty}^{\infty} g(x) f_{X}(x) \, \mathrm{d}x, \end{align*} siempre que esta integral sea absolutamente convergente, y donde $f_{X}\colon\RR\to\RR$ es la función de densidad de $X$.
Demostración. 1. El caso discreto sirve para ilustrar la intuición, pues para cada $x \in X[\Omega]$ se tiene que $g(x) \in (g \circ X)[\Omega]$. Además, ya sabemos que para cada $y \in (g \circ X)[\Omega]$ se cumple que
\begin{align*} \Prob{g(X) = y} &= \Prob{X \in g^{-1}[\{ y \}]} = \sum_{x \in g^{-1}[\{y\}]} \Prob{X = x} \end{align*}
por lo que el valor esperado de $g(X)$ cumple que
\begin{align*} \Esp{g(X)} = \sum_{y \in (g \circ X)[\Omega]} y \Prob{g(X) = y} &= \sum_{y \in (g \circ X)[\Omega]} y \Prob{X \in g^{-1}[\{ y \}]} \\[1em] &= \sum_{y \in (g \circ X)[\Omega]} y {\left( \sum_{x \in g^{-1}[\{y\}]} \Prob{X = x} \right)} \\[1em] &= \sum_{y \in (g \circ X)[\Omega]} \sum_{x \in g^{-1}[\{y\}]} y \Prob{X = x}, \end{align*}
y como $x \in g^{-1}[\{y \}]$ si y sólamente si $g(x) = y$, se sigue que
\begin{align*} \sum_{y \in (g \circ X)[\Omega]} \sum_{x \in g^{-1}[\{y\}]} y \Prob{X = x} &= \sum_{y \in (g \circ X)[\Omega]} \sum_{x \in g^{-1}[\{y\}]} g(x) \Prob{X = x}. \end{align*}
Ahora, observa que de acuerdo con la suma sobre $y$, por cada $y \in (g \circ X)[\Omega]$ hay un sumando que tiene la forma
\[ \sum_{x \in g^{-1}[\{y\}]} g(x) \Prob{X = x}, \]
y cada uno de estos términos es una suma que corre sobre $x$, donde $x \in g^{-1}[\{ y \}]$. Es decir, estamos sumando sobre todos los $y \in (g \circ X)[\Omega]$, y en cada $y$ tomamos la suma sobre todos los $x \in g^{-1}[\{y \}]$. Esto quiere decir que podemos mover a $x$ sobre la unión de todos los $g^{-1}[\{y\}]$, y prescindir de la suma sobre $y$. Esto es,
\begin{align*} \bigcup_{y \in (g \circ X)[\Omega]} g^{-1}[\{y\}] &= g^{-1}{\left[ \bigcup_{y \in (g \circ X)[\Omega]} \{y\} \right]} \\[1em] &= g^{-1}[(g \circ X)[\Omega]] \\[1em] &= g^{-1}[g[X[\Omega]]], \end{align*}
y por propiedades de la imagen inversa, se tiene que $X[\Omega] \subseteq g^{-1}[g[X[\Omega]]]$. Ahora bien, los $x$ que aparecen en la suma son únicamente aquellos que están en $X[\Omega]$, pues de lo contrario son valores que no toma la v.a. $X$. En consecuencia, la suma se puede reducir a
\begin{align*} \sum_{y \in (g \circ X)[\Omega]} \sum_{x \in g^{-1}[\{y\}]} g(x) \Prob{X = x} &= \sum_{x\in X[\Omega]} g(x) \Prob{X = x}, \end{align*}
y así podemos concluir que
\begin{align*} \Esp{g(X)} &= \sum_{x \in X[\Omega]} g(x) \Prob{X = x}, \end{align*}
que es justamente lo que queríamos demostrar. Intuitivamente, esta última igualdad hace sentido, pues $g(X)$ toma el valor $g(x)$ cuando $X$ toma el valor $x$, y el evento en el que eso ocurre tiene probabilidad $\Prob{X = x}$.
La demostración del caso 2. es menos ilustrativa. Cuando $X$ y $g(X)$ son v.a.’s continuas, será necesario hacer una «doble integral», algo con lo que quizás no te hayas encontrado hasta ahora. Esto es algo que (por desgracia) haremos en algunas demostraciones del valor esperado.
Primero, demostraremos el siguiente lema:
Lema. Si $X\colon\Omega\to\RR$ es una v.a. continua tal que para todo $\omega\in\Omega$ se cumple que $X(\omega) \geq 0$ (es decir, $X$ es una v.a. no-negativa), entonces
\begin{align*} \Esp{X} &= \int_{0}^{\infty} [1 − F_{X}(x)] \, \mathrm{d}x, \end{align*}
donde $F_{X}\colon\RR\to\RR$ es la función de distribución de $X$.
Demostración. Sea $D \subseteq \RR^{2}$ el siguiente conjunto:
\begin{align*} D &= \{ \, (x,y) \in \RR^{2} \mid x > y \, \}. \end{align*}
Sea $\mathbf{1}_{D}\colon\RR^{2}\to\RR$ la función dada por
\begin{align*} \mathbf{1}_{D}(x,y) &= \begin{cases} 1 & \text{si $(x,y) \in D$}, \\[1em] 0 & \text{en otro caso}. \end{cases} \end{align*}
Es decir, $\mathbf{1}_{D}(x,y)$ vale $1$ si $(x,y) \in D$, es decir, vale $1$ si $x$ es mayor a $y$; y vale $0$ en caso contrario. Una función de este tipo es conocida como una función indicadora. Ahora, observa que para cualquier $x \in [0, \infty)$ se cumple que
\begin{align*} x &= \int_{0}^{x} 1 \, \mathrm{d}t, \tag{$*$}\end{align*}
pues la integral devuelve como resultado la longitud del intervalo $(0, x)$, que está bien definido, ya que $x \geq 0$. Dicha longitud es precisamente $x − 0 = x$, por lo que la igualdad $(*)$ es verdadera. Ahora, observa que $\mathbf{1}_{D}(x, t) = 1$ si y sólamente si $x > t$, o equivalentemente, si $t \in (-\infty, x)$. Así, tenemos que
\begin{align*} \int_{0}^{x} 1 \, \mathrm{d}t &= \int_{0}^{\infty} \mathbf{1}_{D}(x, t) \, \mathrm{d}t, \end{align*}
pues para $t \in (0, \infty)$, $\mathbf{1}_{D}(x, t) = 1$ sobre $(0, x)$, y es $0$ en otro caso. En conclusión, para cualquier $x \in [0, \infty)$ se cumple que
\begin{align}\label{id:integral} x &= \int_{0}^{\infty} \mathbf{1}_{D}(x, t) \, \mathrm{d}t. \end{align}
Usaremos esta «mañosa» identidad en el valor esperado de $X$. Primero, observa que $X$ es una v.a. no-negativa, así que $f_{X}(x) = 0$ para $x < 0$. En consecuencia, tenemos que
\begin{align*} \Esp{X} &= \int_{-\infty}^{\infty} x f_{X}(x) \, \mathrm{d}x = \int_{0}^{\infty} x f_{X}(x) \, \mathrm{d}x. \end{align*}
Usando la identidad \eqref{id:integral}, obtenemos que
\begin{align*} \int_{0}^{\infty} x f_{X}(x) \, \mathrm{d}x &= \int_{0}^{\infty}{\left( \int_{0}^{\infty} \mathbf{1}_{D}(x, t) \, \mathrm{d}t \right)} f_{X}(x) \, \mathrm{d}x = \int_{0}^{\infty}\int_{0}^{\infty} \mathbf{1}_{D}(x, t) f_{X}(x) \, \mathrm{d}t \, \mathrm{d}x. \end{align*}
Observa que «metimos» a $f_{X}(x)$ dentro de la integral respecto a $t$ debido a que es una constante con respecto a $t$ (únicamente depende de $x$). La trampa que vamos a hacer es cambiar el orden de integración. Esto NO siempre se puede hacer, y la validez de este paso está dada por el teorema de Fubini, que verás en Cálculo Diferencial e Integral IV. Intercambiando el orden de integración, se tiene que
\begin{align*} \int_{0}^{\infty}\int_{0}^{\infty} \mathbf{1}_{D}(x, t) f_{X}(x) \, \mathrm{d}t \, \mathrm{d}x &= \int_{0}^{\infty}\int_{0}^{\infty} \mathbf{1}_{D}(x, t) f_{X}(x) \, \mathrm{d}x \, \mathrm{d}t \end{align*}
Ahora, observa que, para cada $x \in (0, \infty)$, $\mathbf{1}_{D}(x, t) = 1$ si y sólamente si $x > t$, o equivalentemente, si $x \in (t, \infty)$. En consecuencia,
\begin{align*} \int_{0}^{\infty} \mathbf{1}_{D}(x, t) f_{X}(x) \, \mathrm{d}x &= \int_{t}^{\infty} f_{X}(x) \, \mathrm{d}x = \Prob{ X > t } = 1 − F_{X}(t). \end{align*}
Por lo tanto,
\begin{align*}\int_{0}^{\infty}\int_{0}^{\infty} \mathbf{1}_{D}(x, t) f_{X}(x) \, \mathrm{d}x \, \mathrm{d}t &= \int_{0}^{\infty} [1 − F_{X}(t)] \, \mathrm{d}t, \end{align*}
que nos permite concluir que
\begin{align*} \Esp{X} &= \int_{0}^{\infty} [1 − F_{X}(t)] \, \mathrm{d}t, \end{align*}
que es justamente lo que queríamos demostrar.
$\square$
Con este lema podemos demostrar el caso 2. del teorema. Lo que haremos será presentar el caso en el que $g$ es una función no-negativa. De esta manera, $g(X)$ es una v.a. que toma valores no-negativos, y podemos aplicarle el lema. Así, tenemos que
\begin{align*} \Esp{g(X)} &= \int_{0}^{\infty} [1 − F_{X}(x)] \, \mathrm{d}x = \int_{0}^{\infty} \Prob{g(X) > x} \, \mathrm{d}x \end{align*}
Ahora, recuerda que \begin{align*} (g(X) > x) = (g \circ X)^{-1}[(x, \infty)] = X^{-1}[g^{-1}[(x,\infty)]] = (X \in g^{-1}[(x, \infty)], \end{align*} por lo que $\Prob{g(X) > x} = \Prob{X \in g^{-1}[(x, \infty)]}$. Por lo tanto,
\begin{align*} \int_{0}^{\infty} \Prob{g(X) > x} \, \mathrm{d}x &= \int_{0}^{\infty} {\left( \int_{g^{-1}[(x,\infty)]} f_{X}(t) \, \mathrm{d}t \right) } \, \mathrm{d}x \end{align*}
donde la integral de adentro se toma sobre $g^{-1}[(x, \infty)]$, pues esto nos devuelve el valor $\Prob{X \in g^{-1}[(x, \infty)]}$. Nuevamente haremos trampa y cambiaremos el orden de integración. Un detalle adicional es que al cambiar el orden de integración, también cambian los dominios de integración.
\begin{align*} \int_{0}^{\infty} \int_{g^{-1}[(x,\infty)]} f_{X}(t) \, \mathrm{d}t \, \mathrm{d}x &= \int_{g^{-1}[(0,\infty)]} \int_{0}^{g(t)} f_{X}(t) \, \mathrm{d}x \, \mathrm{d}t \end{align*}
Finalmente, como $f_{X}(t)$ es constante respecto a $x$, puede salir como constante de la integral de adentro, y además
\begin{align*} \int_{0}^{g(t)} 1 \, \mathrm{d}x &= g(t) − 0 = g(t), \end{align*}
por lo que
\begin{align*} \int_{g^{-1}[(0,\infty)]} \int_{0}^{g(t)} f_{X}(t) \, \mathrm{d}x \, \mathrm{d}t &= \int_{g^{-1}[(0,\infty)]} {\left(\int_{0}^{g(t)} 1 \, \mathrm{d}x \right)} f_{X}(t) \, \mathrm{d}t \\[1em] &= \int_{g^{-1}[(0,\infty)]} g(t) f_{X}(t) \, \mathrm{d}t, \\[1em] &= \int_{-\infty}^{\infty} g(t) f_{X}(t) \, \mathrm{d}t,\end{align*}
donde $g^{-1}[(0,\infty)] = \RR$ porque $g$ es una función no-negativa. Así, finalmente podemos concluir que
\begin{align*} \Esp{g(X)} &= \int_{-\infty}^{\infty} g(t) f_{X}(t) \, \mathrm{d}t, \end{align*}
que es justo lo que queríamos demostrar.
$\square$
Como comentamos anteriormente, el teorema que acabamos de demostrar es conocido como la ley del estadístico inconsciente. De acuerdo con Sheldon M. Ross, en su libro Introduction to Probability Models (1980, 1a Ed.) «Esta ley recibió su nombre por los estadísticos ‘inconscientes’ que la han utilizado como si fuese la definición de $\Esp{g(X)}$».
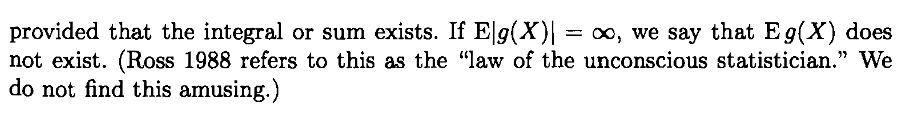
Independientemente de esto, la ley del estadístico inconsciente es un resultado muy importante, y la utilizaremos mucho de aquí en adelante.
Ejemplos del uso de la ley del estadístico inconsciente
Ejemplo 1. Sea \(U\) una v.a. con función de densidad \(f_{U}\) dada por
\begin{align*} f_{U}(u) &= \begin{cases} \lambda e ^{ − \lambda x} & \text{si \(x > 0\),} \\[1em] 0 & \text{en otro caso,} \end{cases} \end{align*}
con \(\lambda > 1\). Obtengamos el valor esperado de \(e^{U}\). Para ello, usemos la ley del estadístico inconsciente:
\begin{align*} \Esp{U} &= \int_{0}^{\infty} e^{u} \lambda e^{-\lambda u} \, \mathrm{d}u \\[1em] &= \int_{0}^{\infty} \lambda e^{-\lambda u + u} \, \mathrm{d}u\\[1em] &= \lambda \int_{0}^{\infty} e^{(1 − \lambda)u} \, \mathrm{d}u.\end{align*}
Para resolver esta integral, observa que se trata de una integral casi inmediata, únicamente le falta el factor \(1 − \lambda\), por lo que multiplicamos por \(1\):
\begin{align*} \lambda \int_{0}^{\infty} e^{(1 − \lambda)u} \, \mathrm{d}u &= \lambda \int_{0}^{\infty} {\left(\frac{ 1 − \lambda }{ 1 − \lambda }\right)}e^{(1 − \lambda)u} \, \mathrm{d}u \\[1em] &= \frac{\lambda}{1 − \lambda} \int_{0}^{\infty} ( 1 − \lambda)e^{( 1 − \lambda )u} \, \mathrm{d}u \\[1em] &= \frac{\lambda}{1 − \lambda} {\left( e^{( 1 − \lambda )u} \right)} \Bigg|_{u=0}^{\infty} \\[1em] &= \frac{\lambda}{1 − \lambda} {\left( 0 − 1 \right)} \\[1em] \frac{\lambda}{1 − \lambda} {\left(− 1 \right)} \\[1em] &= \frac{\lambda}{\lambda − 1}, \end{align*}
así que concluimos que
\begin{align*} \Esp{e^{U}} = \frac{\lambda}{\lambda − 1}. \end{align*}
Ejemplo 2. Sea \(N\) una variable aleatoria con función de masa de probabilidad (f.m.p.) \(f_{N}\) dada por
\begin{align*} f_{N}(n) &= \begin{cases} (1 − p)^{n}p & \text{si \(n \in \mathbb{N}\),} \\[1em] 0 & \text{en otro caso,} \end{cases}\end{align*}
con \(p \in (0,1)\). Obtengamos el valor esperado de \(N^{2}\). Por la ley del estadístico inconsciente, tenemos que
\begin{align} \label{eq:serie1} \Esp{N^{2}} &= \sum_{n=0}^{\infty} n^{2} (1 − p)^{n}p. \end{align}
Como usualmente pasa con los valores esperados de v.a.’s que toman el valor \(0\), el primer término de la serie \eqref{eq:serie1} es \(0\), así que la igualdad anterior pasa a ser
\begin{align*} \Esp{N^{2}} &= \sum_{n=1}^{\infty} n^{2} (1 − p)^{n}p. \end{align*}
Para obtener el valor de la serie anterior, vamos a utilizar una expresión equivalente basada en la siguiente identidad: sea \(n\in\mathbb{N}^{+}\), entonces se cumple que
\begin{align} \label{eq:identidad} n^{2} − (n − 1)^{2} &= 2n − 1. \end{align}
Ahora, observa con atención las siguientes dos series.
\begin{align} \label{eq:serie2} \Esp{N^{2}} &= \sum_{n=1}^{\infty} n^{2} (1 − p)^{n}p = (1 − p)p + 4(1 − p)^{2}p + 9 (1 − p)^{3}p + \cdots \\[1em] \label{eq:serie3} (1 − p)\Esp{N^{2}} &= \sum_{n=1}^{\infty} n^{2} (1 − p)^{n+1}p = (1 − p)^{2}p + 4 (1 − p)^{3}p + 9 (1 − p)^{4}p + \cdots \end{align}
Es decir, multiplicar la serie \eqref{eq:serie2} por \( (1 − p)\) nos da la \eqref{eq:serie3}, que simplemente «desplaza» el índice por \(1\). Por ello, se tiene que
\begin{align*} \Esp{N^{2}} − (1 − p)\Esp{N^{2}} &= (1 − p)p + 3 (1 − p)^{2}p + 5 (1 − p)^{3}p + \cdots = \sum_{n=1}^{\infty} (n^{2} − (n − 1)^{2})(1 − p)^{n}p, \end{align*}
donde tal vez alcances a notar cómo se usará la identidad \eqref{eq:identidad}. En efecto, por esta identidad tenemos que
\begin{align*} \Esp{N^{2}} − (1 − p)\Esp{N^{2}} &= \sum_{n=1}^{\infty} (n^{2} − (n − 1)^{2})(1 − p)^{n}p = \sum_{n=1}^{\infty} (2n − 1)(1 − p)^{n}p \end{align*}
Además, nota que \(\Esp{N^{2}} − (1 − p)\Esp{N^{2}} = p\Esp{N^{2}}\), así que
\begin{align} \label{eq:serie4} p\Esp{N^{2}} &= \sum_{n=1}^{\infty} (2n − 1)(1 − p)^{n}p. \end{align}
Usaremos la igualdad \eqref{eq:serie4} más adelante. Por ahora, centraremos nuestra atención en desarrollar la serie en \eqref{eq:serie4}. Primero, recuerda que la serie debe de ser convergente para que los siguientes pasos tengan sentido, así que revisa la tarea moral en caso de que lo dudes. Así pues, tenemos que
\begin{align*} \sum_{n=1}^{\infty} (2n − 1)(1 − p)^{n}p &= \sum_{n=1}^{\infty} 2n(1 − p)^{n}p − \sum_{n=1}^{\infty} (1 − p)^{n}p \\[1em] &= 2\underbrace{\sum_{n=1}^{\infty} n(1 − p)^{n}p}_{(*)} − \underbrace{\sum_{n=1}^{\infty} (1 − p)^{n}p}_{(**)}. \end{align*}
Por un lado, observa que la expresión \((*)\) es el valor esperado de \(N\) (y ya calculamos ese valor esperado en la entrada pasada), así que \((*) = \frac{ 1 − p }{p}\). Por otro lado, la expresión \((*)\) es casi la suma de las probabilidades de \(N\), por lo que debería de ser \(1\) menos el término en \(0\), ya que la suma empieza en \(1\). Veámoslo:
\begin{align*} \sum_{n=1}^{\infty} (1 − p)^{n}p &= p − p + \sum_{n=1}^{\infty} (1 − p)^{n}p \\[1em] &= {\left[\sum_{n=0}^{\infty} (1 − p)^{n}p\right]} − p \\[1em] &= p\underbrace{\left[\sum_{n=0}^{\infty} (1 − p)^{n}\right]}_{\text{serie geométrica}} − p \\[1em] &= p \frac{1}{1 − (1 − p)} − p \\[1em] &= p\frac{1}{p} − p \\[1em] &= 1 − p. \end{align*}
Por lo tanto, tenemos que
\begin{align*} \sum_{n=1}^{\infty} (2n − 1)(1 − p)^{n}p &= 2\underbrace{\sum_{n=1}^{\infty} n(1 − p)^{n}p}_{(*)} − \underbrace{\sum_{n=1}^{\infty} (1 − p)^{n}p}_{(**)} \\[1em] &= \frac{2 (1 − p) }{p} − (1 − p) \\[1em] &= \frac{2(1 − p) − p(1 − p)}{p} \\[1em] &= \frac{2 − 2p − p + p^{2} }{p} \\[1em] &= \frac{2 − 3p + p^{2}}{p} \\[1em] &= \frac{(2 − p)(1 − p)}{p}. \end{align*}
En consecuencia, volviendo a \eqref{eq:serie4}, tenemos que
\begin{align*} p\Esp{N^{2}} &= \frac{(2 − p)(1 − p)}{p}, \end{align*}
por lo que en conclusión
\begin{align*} \Esp{N^{2}} &= \frac{(2 − p)(1 − p)}{p^{2}}, \end{align*}
que es justamente lo que queríamos obtener.
Tarea moral
Los siguientes ejercicios son opcionales. Es decir, no formarán parte de tu calificación. Sin embargo, te recomiendo resolverlos para que desarrolles tu dominio de los conceptos abordados en esta entrada.
- Demuestra el caso 2. de la ley del estadístico inconsciente cuando $g$ es una función cualquiera. Sugerencia: Toma la siguiente descomposición de $g$: definimos la parte positiva de $g$, $g^{+}\colon\RR\to\RR$, como sigue: \begin{align*} g^{+}(x) &= \max{\{ g(x), 0 \}} & \text{para cada $x \in \RR$},\end{align*} y definimos la parte negativa de $g$, $g^{-}\colon\RR\to\RR$, como sigue: \begin{align*} g^{-}(x) &= \max{\{ -g(x), 0 \}} & \text{para cada $x \in \RR$}.\end{align*} Verifica que $g$ puede escribirse en términos de $g^{+}$ y $g^{-}$ como\begin{align*} g = g^{+} − g^{-}, \end{align*}y nota que tanto $g^{+}$ como $g^{-}$ son funciones no-negativas. Concluye utilizando lo que demostramos en esta entrada.
- Verifica que la serie \eqref{eq:serie1} es convergente. Sugerencia: Utiliza algún criterio de convergencia como el de d’Alembert.
- Demuestra la validez de la identidad \eqref{eq:identidad}.
Más adelante…
La ley del estadísico inconsciente es un teorema muy útil en contextos teóricos y aplicados. De hecho, la utilizaremos con mucha frecuencia en la Unidad 3, ya que veremos algunas características de algunas distribuciones de probabilidad importantes.
Por otro lado, en la siguiente entrada veremos más propiedades del valor esperado, centrando nuestra atención en aquellas propiedades que involucran a más de una variable aleatoria.
Entradas relacionadas
- Ir a Probabilidad I
- Entrada anterior del curso: Valor Esperado de una Variable Aleatoria
- Siguiente entrada del curso: Interacciones Entre Dos Variables Aleatorias
