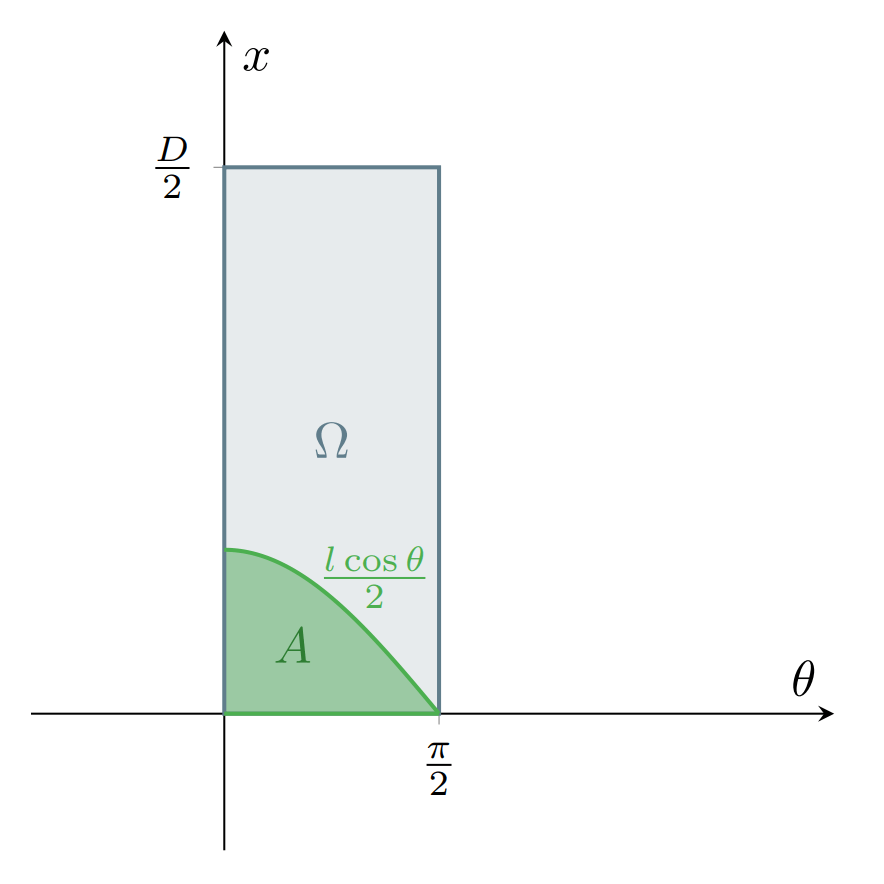Introducción

En la entrada pasada concluimos el estudio de algunas propiedades básicas de una medida de probabilidad. A partir de estas propiedades serás capaz de demostrar muchísimas otras más, que probablemente te encontrarás en tareas, exámenes o en las secciones de ejercicios de tus libros. Por el momento, sigamos con el contenido del curso.

Lo que sigue en el curso es ver tres enfoques de la probabilidad: la probabilidad geométrica, el enfoque frecuentista, y la definición clásica de la probabilidad. Así pues, en esta entrada veremos lo que corresponde a la probabilidad geométrica. Algunos aspectos para tratar con total formalidad este tema son más avanzados. Por ello, veremos este tema «por encima», omitiendo algunas formalidades.

Hay una sección en esta entrada cuyo título lleva un asterisco (*). Cuando las leas, no te preocupes si no entiendes las formalidades, lo importante es que entiendas los resultados.

Motivación de la probabilidad geométrica

Seguramente te ha tocado jugar o espectar algún juego de lanzar cosas. Por ejemplo, el lanzamiento de dardos, o el tiro con arco. La puntuación que obtienes en un juego de este tipo se basa en tu precisión. Es decir, tú arrojas o disparas un objeto hacia una superficie, y obtienes puntos basado en la región de esa superficie a la que le atinaste. Como ejemplo, está la diana de un juego de tiro con arco:

Evidentemente, cuando estás jugando a los dardos o al tiro con arco, usas tu habilidad para intentar juntar la mayor puntuación posible. Sin embargo, podemos volverlo un tema probabilista. ¿Qué pasa si decidimos arrojar un dardo, o disparar una flecha al azar? En otras palabras, que dentro de la superficie dada, escojamos un punto al azar. ¿Cómo determinamos la probabilidad de que el punto elegido caiga dentro de una región dada?

Un primer modelo para acercarnos a este problema es trabajar en ${\mathbb{R}}^2$, el plano euclidiano. Luego, tomar una región acotada de ${\mathbb{R}}^2$, digamos, $\mathrm{\Omega }$. Además, supondremos que el punto se elige de manera «uniforme» sobre la región $\mathrm{\Omega }$. Es decir, que la probabilidad de cualquier subconjunto de $\mathrm{\Omega }$ es proporcional a su «área». Por ejemplo, para modelar una diana, podemos tomar a $\mathrm{\Omega }$ como un círculo.

Un poco sobre la medida y el σ-álgebra que se utiliza*

Por motivos de tiempo y prerrequisitos, no es posible tratar con mucho detalle la medida ni el σ-álgebra que usaríamos en ${\mathbb{R}}^2$. Por ello, recomendamos que de esta sección extraigas las ideas y resultados, y que no hagas un esfuerzo excesivo por entender la formalidad. Lo que haremos es partir de los rectángulos en $2$ dimensiones, pues es fácil definir su área.

---

Definición. Un rectángulo bidimensional cerrado es un subconjunto $R\subseteq {\mathbb{R}}^2$ de la forma

$$R=[a_1,b_1]\times [a_2,b_2],$$

donde $a_1$, $b_1$, $a_2$ y $b_2\in \mathbb{R}$. En consecuencia, el área de $R$ es

$$\mu (R)=(b_1-a_1)(b_2-a_2).$$

---

Consideraremos a $\mathrm{\varnothing }$ como un rectángulo con $\mu (\mathrm{\varnothing })=0$. Denotaremos al conjunto de todos los rectángulos bidimensionales cerrados por $\mathcal{R}({\mathbb{R}}^2)$. Veremos muy por encima la manera en que se construye matemáticamente la noción de «área». Lo que haremos será aproximar el área de cualquier subconjunto $E$ de ${\mathbb{R}}^2$ por afuera, a través del área de familias de rectángulos que contengan a $E$.

---

Definición. La medida exterior de Lebesgue ${\mu }^{\ast }(E)$ de un subconjunto $E\subseteq {\mathbb{R}}^2$, es

$${\mu }^{\ast }(E)=inf\{\sum _{k=1}^{\mathrm{\infty }}\mu (R_k)|E\subseteq \bigcup _{k=1}^{\mathrm{\infty }}{R}_k,R_k\in \mathcal{R}({\mathbb{R}}^2)\},$$

donde el ínfimo se toma sobre las familias numerables de rectángulos cuya unión contiene a $E$. La función ${\mu }^{\ast }:\mathcal{P}({\mathbb{R}}^2⟶[0,\mathrm{\infty }]$ es llamada la medida exterior de Lebesgue.

---

Varios conceptos en la teoría de la medida reciben su nombre en honor a Henri Lebesgue, un importantísimo matemático francés que desarrolló toda una teoría de integración de funciones.

En la definición anterior, se admite que ${\mu }^{\ast }(E)$ valga $\mathrm{\infty }$. Esto es algo que no nos preocupará mucho en la probabilidad geométrica, pero es importante tenerlo en cuenta. Así, la función ${\mu }^{\ast }$ nos da el área de cualquier región «agradable» de ${\mathbb{R}}^n$, y la obtiene aproximando por afuera con rectángulos.

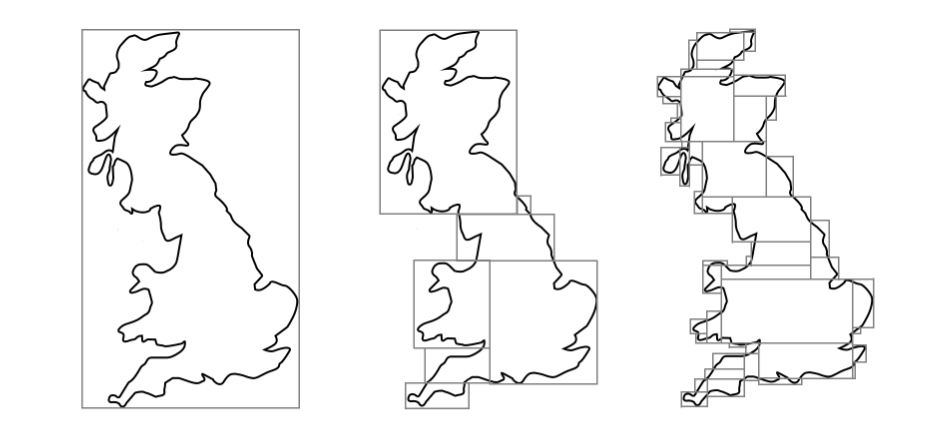
Ahora, lo que nos interesa es conseguir un σ-álgebra sobre la que la medida exterior de Lebesgue sea, efectivamente, una medida. La siguiente es la definición de Carathéodory (pues fue formulada por el matemático griego Constantin Carathéodory) de medibilidad. Esto es, los conjuntos que satisfacen este criterio son a los que se les podrá medir su «área».

---

Definición. Un subconjunto $A\subseteq {\mathbb{R}}^2$ es Lebesgue-medible si para cualquier subconjunto $E\subseteq {\mathbb{R}}^2$ se cumple que

$${\mu }^{\ast }(E)={\mu }^{\ast }(E\cap A)+{\mu }^{\ast }(E\cap A^{\mathsf{c}}).$$

---

Denotaremos al conjunto de todos los conjuntos Lebesgue-medibles en ${\mathbb{R}}^2$ por $\mathcal{L}({\mathbb{R}}^2)$. Esta condición puede interpretarse como que un conjunto es medible si divide a otros conjuntos de «buena» manera. Resulta que $\mathcal{L}({\mathbb{R}}^2)$ es un σ-álgebra. Además, también se tiene que ${\mu }^{\ast }$ restringida a $\mathcal{L}({\mathbb{R}}^2)$ es una medida (no de probabilidad, simplemente medida. Es lo mismo pero sin pedir que la medida de ${\mathbb{R}}^2$ sea $1$). Así, se llega a la siguiente definición.

---

Definición. La función $\lambda :\mathcal{L}({\mathbb{R}}^2)⟶[0,\mathrm{\infty }]$ definida como

$$\lambda ={{\mu }^{\ast }|}_{\mathcal{L}({\mathbb{R}}^2)},$$

la restricción de ${\mu }^{\ast }$ a $\mathcal{L}({\mathbb{R}}^2)$, es llamada la medida bidimensional de Lebesgue en ${\mathbb{R}}^2$.

---

La medida de Lebesgue asigna a cada región $E\subseteq \mathcal{L}({\mathbb{R}}^2)$ (las cuales son regiones «bonitas», a las que se les puede asignar un área, en el sentido de la definición de Lebesgue-medible) el valor $\lambda (E)$, que corresponde a su área.

Definición de la probabilidad geométrica

Así, si ahora tomamos alguna región de ${\mathbb{R}}^2$ para la cual su área está bien definida, podemos construir una medida de probabilidad en la que la probabilidad de cada sub-región es proporcional a su área. Si $\mathrm{\Omega }$ es un subconjunto acotado de ${\mathbb{R}}^2$ que es Lebesgue-medible, entonces su área es finita. Más aún, podemos considerar a

$$\mathcal{L}(\mathrm{\Omega })=\mathcal{P}(\mathrm{\Omega })\cap \mathcal{L}({\mathbb{R}}^2),$$

el conjunto de todos los subconjuntos de $\mathrm{\Omega }$ que son Lebesgue-medibles, este es un σ-álgebra sobre $\mathrm{\Omega }$. En consecuencia, podemos definir una medida, y dar lugar a un espacio de probabilidad.

---

Definición. Sea $\mathrm{\Omega }\subseteq {\mathbb{R}}^2$ un conjunto acotado y con área bien definida mayor a $0$. Sea $\mathcal{L}(\mathrm{\Omega })$ el conjunto de todos los subconjuntos de $\mathrm{\Omega }$ con área bien definida. Se define la probabilidad geométrica $\mathbb{P}:\mathcal{L}(\mathrm{\Omega })⟶\mathbb{R}$ como sigue. Para cada $A\in \mathcal{L}(\mathrm{\Omega })$, se define $\mathbb{P}\left(A\right)$ como

$$\mathbb{P}\left(A\right)=\frac{\text{Area}(A)}{\text{Area}(\mathrm{\Omega })}.$$

---

En la definición anterior, el «área» de $A$, que denotamos por $\text{Area}(A)$, es precisamente $\lambda (A)$, la medida bidimensional de Lebesgue. No centres mucho tu atención en el uso de los conjuntos Lebesgue-medibles ni en la medida de Lebesgue. Nuestra intención es exhibir que la noción de «área» puede ser formalizada matemáticamente, y despertar tu interés por estudiar estos temas con más profundidad. Lo importante con lo que te debes de quedar es que, a cada subconjunto de $\mathrm{\Omega }$ con área bien definida, se le asigna una probabilidad que es la proporción entre su área y el área de $\mathrm{\Omega }$.

Esta medida de probabilidad asume que se cumple una propiedad llamada equiprobabilidad. Esto es, para cada $A\in \mathcal{L}(\mathrm{\Omega })$, no importa cuáles sean los elementos de $A$, lo único que importa para determinar su probabilidad es su área.

Un primer ejemplo de probabilidad geométrica

Ejemplo. Imagina que vas a tomar un autobús en una parada. Supongamos que tú y el autobús llegarán en tiempos aleatorios a la parada, entre las 12pm y la 1pm. Es decir, los tiempos de llegada tuyo y del autobús son valores $x$, $y\in [0,60]$, pues el tiempo (en minutos) entre las 12pm y la 1pm es de $60$ minutos. Además, supongamos que cuando el autobús llega, permanece en la parada $5$ minutos antes de irse; y cuando tú llegas, esperas $20$ minutos antes de irte si el autobús no llega. ¿Cuál es la probabilidad de que tomes el autobús?

Para resolver este problema, observa que $\mathrm{\Omega }$ en este puede considerarse como

$$\mathrm{\Omega }=[0,60]\times [0,60]=\{(x,y)\in {\mathbb{R}}^2\mid x\in [0,60]\wedge y\in [0,60]\},$$

y que dado un par ordenado $(x,y)$, $x$ es tu tiempo de llegada y $y$ es el tiempo de llegada del autobús. Gráficamente, todos los posibles resultados están dentro de un cuadrado:

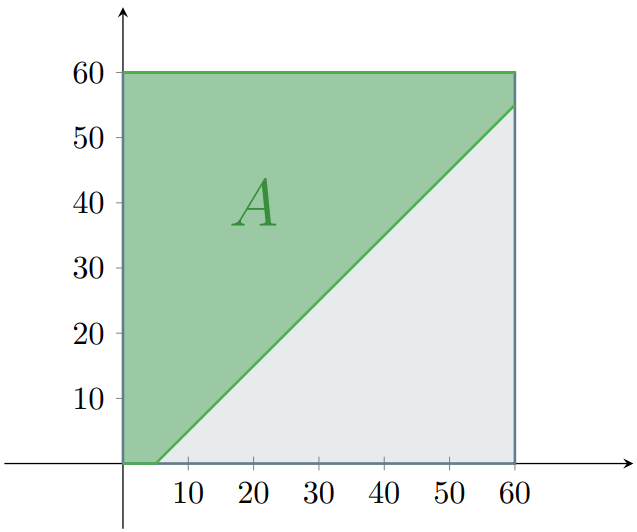
Luego, tenemos que encontrar las regiones que corresponden al evento en el que tú y el autobús coinciden. Primero, sabemos que el autobús espera $5$ minutos después de llegar, por lo que tú debes de llegar dentro de esos $5$ minutos que espera. Es decir, $x$, tu tiempo de llegada, debe de ser menor o igual a $y+5$. Así, $x\le y+5$, o equivalentemente, $y\ge x–5$. Este sería un evento $A$, dado como sigue:

$$A=\{(x,y)\in \mathrm{\Omega }\mid y\ge x–5\}.$$

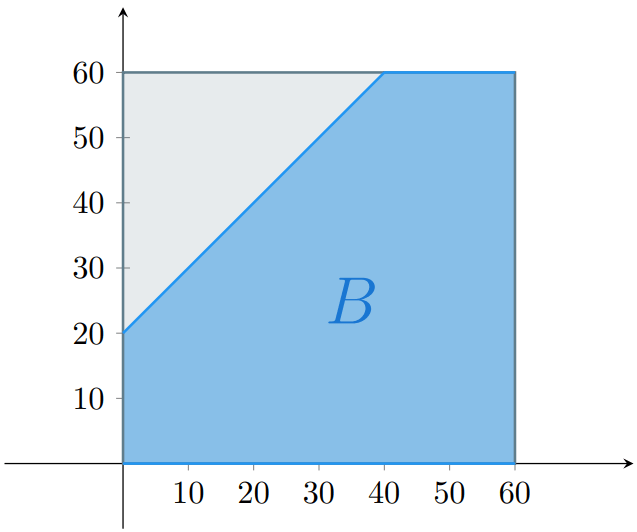
Por otro lado, tú esperas el autobús por $20$ minutos, por lo que no puedes llegar más de $20$ minutos antes que el autobús. Es decir, $x$ debe de ser mayor o igual a $y-20$. Así, $x\ge y-20$, o equivalentemente, $y\le x+20$. Por ello, el evento $B$ que representa a esta situación es

$$B=\{(x,y)\in \mathrm{\Omega }\mid y\le x+20\}.$$

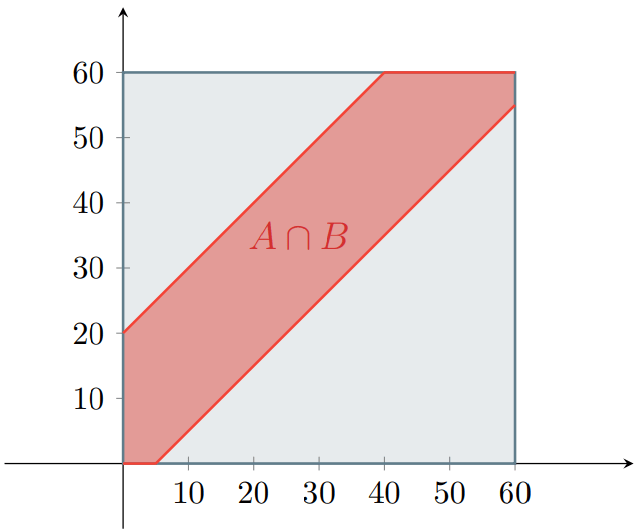
Intersecando ambas regiones obtenemos la región en donde tú y el autobús coinciden.

Y podemos utilizar la probabilidad geométrica para dar solución a este problema: la probabilidad de que tomes el autobús es el área de esta última región dividida entre el área total. Podemos utilizar la regla de complementación para facilitar el cálculo, pues las regiones en donde no tomas el autobús son triángulos y es más fácil calcular su área.

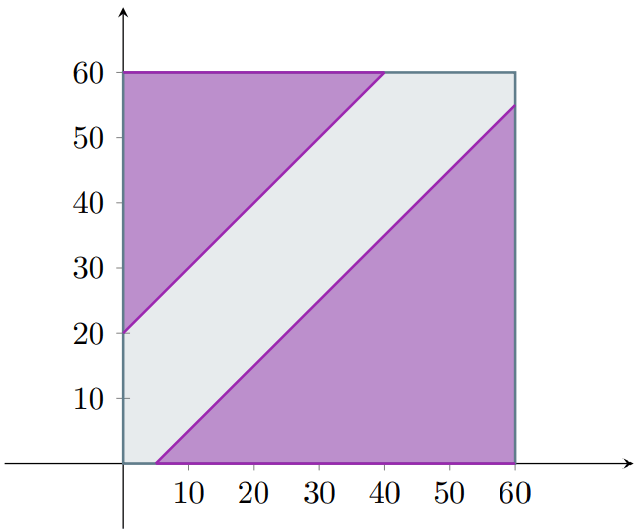
La región de arriba es un triángulo rectángulo cuyos catetos miden $40$, así que su área es $\frac{{40}^2}{2}$. De igual forma, la región de abajo es un triángulo rectángulo cuyos catetos miden $55$, por lo que su área es $\frac{{55}^2}{2}$. Por otro lado, el área de $\mathrm{\Omega }$ es ${60}^2$, pues es un cuadrado cuyos lados miden $60$. Así, tenemos que

$$\begin{array}{rl}\mathbb{P}((A\cap B{)}^{\mathsf{c}})& =\frac{\frac{{40}^2}{2}+\frac{{55}^2}{2}}{{60}^2}\\ & =\frac{{40}^2+{55}^2}{(2)(60{)}^2}\\ & =\frac{1600+3025}{7200}\\ & =\frac{4625}{7200}.\end{array}$$

Y como $\mathbb{P}(A\cap B)=1-\mathbb{P}((A\cap B{)}^{\mathsf{c}})$, tenemos que

$$\mathbb{P}(A\cap B)=1-\frac{4625}{7200}=\frac{7200+4625}{7200}=\frac{2575}{7200}=\frac{103}{288}\approx 0.35764.$$

En conclusión, la probabilidad de que tomes el autobús es aproximadamente $0.35764$, o alternativamente, es aproximadamente un $35.764\mathrm{\%}$.

El problema de la aguja de Buffon

En el siglo XVIII, el naturalista francés Georges-Louis Leclerc formuló un problema con un resultado muy interesante.

Supón que tenemos un piso hecho de bandas de madera, todas con la misma anchura, y dejamos caer una aguja al azar sobre el piso. ¿Cuál es la probabilidad de que la aguja caiga sobre la línea entre dos bandas?

Este problema es conocido como la aguja de Buffon en honor a su creador: Georges-Louis Leclerc, conde de Buffon. Una solución utilizando algunos hechos geométricos fue publicada por Joseph-Émile Barbier en 1860 para el caso en el que la longitud de la aguja es menor a la anchura de las tablas de madera. Para resolver este problema, sea $l$ la longitud de la aguja y sea $D$ el ancho de cada banda de madera. Asumiremos que $0<l<D$.

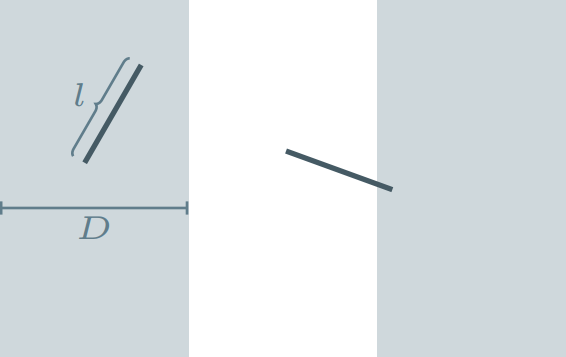
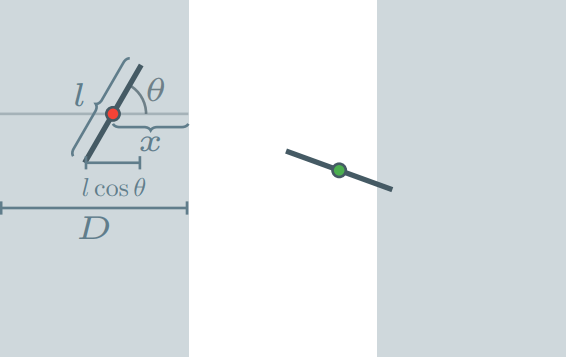
Ahora, sea $\theta$ el ángulo agudo que forma la aguja con el eje horizontal, y sea $x$ la distancia entre el centro de la aguja y la línea entre dos bandas más cercana.

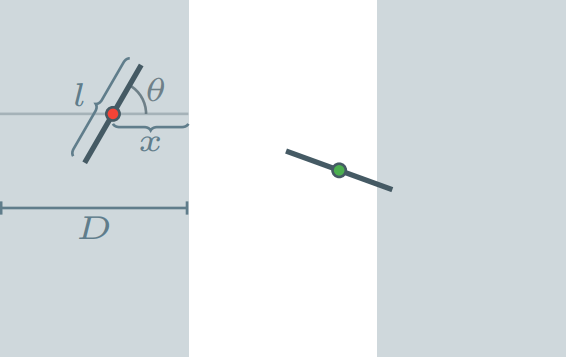
Observa que la aguja cae sobre la línea entre dos bandas si y sólamente si $x\le \frac{l\cos \theta }{2}$. Esto pasa porque $l\cos \theta$ es la distancia horizontal de la aguja, así que $\frac{l\cos \theta }{2}$ es la distancia entre el centro de la aguja y la proyección sobre el eje horizontal de sus extremos. Por lo tanto, si la distancia entre el centro de la aguja y la línea entre dos bandas más cercana es menor o igual a $\frac{l\cos \theta }{2}$, la aguja atraviesa esta línea.

Ahora, asumimos que los valores de $x$ y $\theta$ son aleatorios. Además, se debe de cumplir que $0<x<\frac{D}{2}$, pues $0<l<D$ (así que la distancia a la línea entre bandas más cercana es menor a $\frac{D}{2}$); y además $0<\theta <\frac{\pi }{2}$. Por lo tanto, el espacio muestral de este fenómeno puede verse como

$$\mathrm{\Omega }=\{(\theta ,x)\in {\mathbb{R}}^2|0<\theta <\frac{\pi }{2}\wedge 0<x<\frac{D}{2}\}=(0,\frac{\pi }{2})\times (0,\frac{D}{2}).$$

Y vimos que la aguja cae sobre la línea entre dos bandas si y sólamente si $x\le \frac{l\cos \theta }{2}$, por lo que el evento $A$ que nos interesa es

$$A=\{(\theta ,x)\in \mathrm{\Omega }|x\le \frac{l\cos \theta }{2}\}.$$

Observa que el área de $A$ se ve como en la siguiente figura:

Así, el área de $A$ la podemos calcular integrando la función $\frac{l\cos \theta }{2}$ de $0$ a $\frac{\pi }{2}$. Así,

$$\begin{array}{rl}\text{Area}(A)& ={\int }_0^{\frac{\pi }{2}}\frac{l}{2}\cos \theta \text{d}\theta \\ & =\frac{l}{2}[\sin \frac{\pi }{2}-\sin 0]\\ & =\frac{l}{2}.\end{array}$$

Por otro lado, el área de todo $\mathrm{\Omega }$ es

$$\text{Area}(\mathrm{\Omega })=\left(\frac{D}{2}\right)\left(\frac{\pi }{2}\right)=\frac{\pi D}{4}.$$

Así, se tiene que la probabilidad geométrica de $A$, $\mathbb{P}\left(A\right)$, es

$$\mathbb{P}\left(A\right)=\frac{\text{Area}(A)}{\text{Area}(\mathrm{\Omega })}=\frac{\frac{l}{2}}{\frac{\pi D}{4}}=\frac{l}{2}\frac{4}{\pi D}=\frac{2l}{\pi D}.$$

Una consecuencia interesante de la solución a este problema es que la probabilidad resultante involucra a $\pi$, una constante matemática muy importante. Mucho más adelante veremos una forma curiosa de aproximar el valor de $\pi$ repitiendo el experimento de la aguja de Buffon muchas veces.

Tarea moral

Los siguientes ejercicios son opcionales. Es decir, no formarán parte de tu calificación. Sin embargo, te recomiendo resolverlos para que desarrolles tu dominio de los conceptos abordados en esta entrada.

1. Sea $\mathrm{\Omega }\subseteq {\mathbb{R}}^2$ un conjunto acotado y con área bien definida. Sea $\mathcal{L}(\mathrm{\Omega })$ el conjunto de todos los subconjuntos de $\mathrm{\Omega }$ que son Lebesgue-medibles, y sea $\mathbb{P}:\mathcal{L}(\mathrm{\Omega })⟶\mathbb{R}$ la probabilidad geométrica. Es decir, para cada $A\in \mathcal{L}(\mathrm{\Omega })$, se define $\mathbb{P}\left(A\right)$ como $$\mathbb{P}\left(A\right)=\frac{\text{Area}(A)}{\text{Area}(\mathrm{\Omega })}.$$Explica por qué $(\mathrm{\Omega },\mathcal{L}(\mathrm{\Omega }),\mathbb{P})$ es un espacio de probabilidad. En particular, como ya acordamos que $\mathcal{L}(\mathrm{\Omega })$ es un σ-álgebra, basta con que expliques por qué la probabilidad geométrica es una medida de probabilidad.
2. Vuelve a hacer el ejercicio del autobús pero ahora supón que tú esperas al autobús durante $15$ minutos, y el autobús espera $7$ minutos.
3. En el problema de la aguja de Buffon, explica por qué si $l<D$ (esto es, la longitud de la aguja es menor que la anchura de las bandas), podemos concluir que $x$ (la distancia entre el centro de la aguja y la línea entre dos bandas más cercana) es menor a $\frac{D}{2}$.
4. Explica por qué si la longitud de la aguja $l$ es mayor a $D$ no podemos solucionar el problema de la forma en que lo hicimos.

Más adelante…

La probabilidad geométrica presenta una herramienta muy útil para dar solución a problemas con una interpretación espacial directa, como es el caso del problema de la aguja de Buffon. Además, resulta útil como una herramienta auxiliar para resolver ejercicios que no necesariamente tienen una interpretación visual directa, como el ejemplo del autobús. En conclusión, es una herramienta útil, pero que debes de tener cuidado con sus hipótesis: supone equiprobabilidad sobre el espacio muestral $\mathrm{\Omega }$.

En la materia de Probabilidad II estudiarás a fondo la aleatoriedad en varias variables. Esto te dará herramientas más poderosas para describir la aleatoriedad sobre ${\mathbb{R}}^2$ (y más allá) sin suponer que el espacio muestral es equiprobable.

Por lo pronto, en la siguiente entrada veremos un enfoque distinto de la probabilidad: la probabilidad frecuentista.

Entradas relacionadas

• Ir a Probabilidad I
• Entrada anterior del curso: Propiedades de una Medida de Probabilidad, parte 2
• Siguiente entrada del curso: