(Trabajo de titulación asesorado por la Dra. Diana Avella Alaminos)
Introducción
En esta nota estudiaremos las secuencias ordenadas de $m$ entradas, llenadas con los $n$ objetos de un determinado conjunto pero de modo que no se tengan entradas repetidas. Formalmente serán funciones inyectivas del conjunto de los primeros $m$ naturales, en el conjunto de $n$ objetos.
Definición
Sean $n,m\in \mathbb N^+$. Dado un conjunto $A=\set{a_1,\dotsc ,a_n}$ con $n$ elementos, las ordenaciones de los elementos de $A$ tomados de $m$ en $m$ son las funciones inyectivas de $\set{1,\dotsc, m}$ en $A$. Al número de ordenaciones de los elementos de un conjunto con $n$ elementos, tomados de $m$ en $m$, lo denotaremos por $O_{n}^{m}$, es decir, dado $A=\set{a_1,\dotsc ,a_n}$ un conjunto con $n$ elementos
$O_{n}^{m}=\#\set{f\mid f:\set{1,\dotsc, m}\to \set{a_1,\dotsc ,a_n}, con\\\ f \\\ inyectiva}$
Observa que, gracias a lo que estudiamos acerca de las funciones invectivas, sabemos que si $m>n$ entonces no existen funciones inyectivas de $\set{1,\dotsc, m}$ en $A$ y en consecuencia $O_{n}^{m}$ es cero.
Ejemplo
¿Cuántas banderas tricolores se pueden formar con los colores rojo, naranja, verde, azul y morado?
Consideremos la bandera tricolor de colores rojo, azul, naranja.

En el lugar $1$ asignamos el rojo, en el $2$ el azul y en el $3$ el naranja. Podemos verla como una función de $\set{1,2,3}$ en $A$, con $A$ el conjunto formado por los colores rojo, naranja, verde, azul y morado, es decir $A=\{rojo, naranja, verde, azul,morado\}$. En este caso la función sería:
$f: \set{1,2,3} \to A$ con $f(1)=rojo$, $f(2)=azul$, $f(3)=naranja.$
Veamos primero cuántas banderas tricolor hay que terminen en naranja.
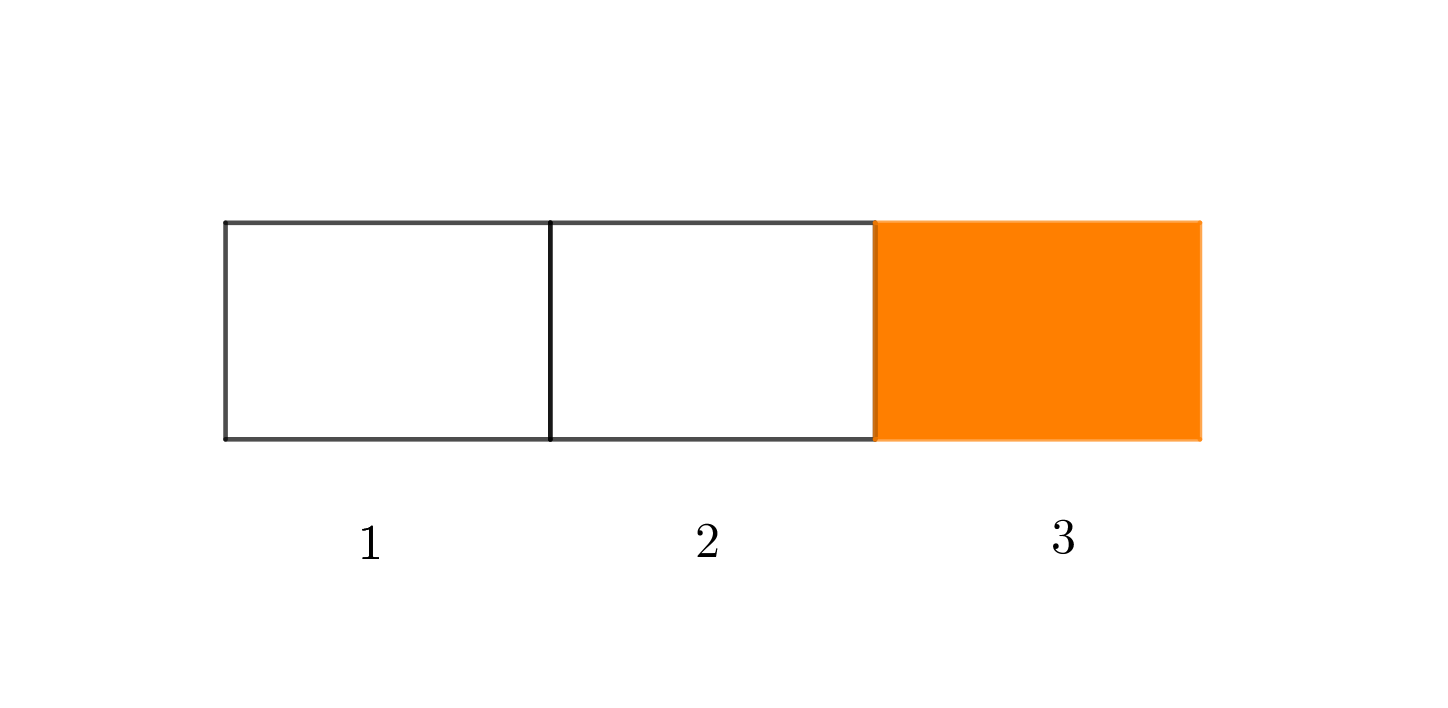
Para ello debemos considerar todas las posibles maneras de iniciar una bandera que termine en naranja, lo cual corresponde a todas las formas de crear una bandera bicolor con los colores restantes. Las banderas bicolores formadas con los colores rojo, verde, azul o morado son:
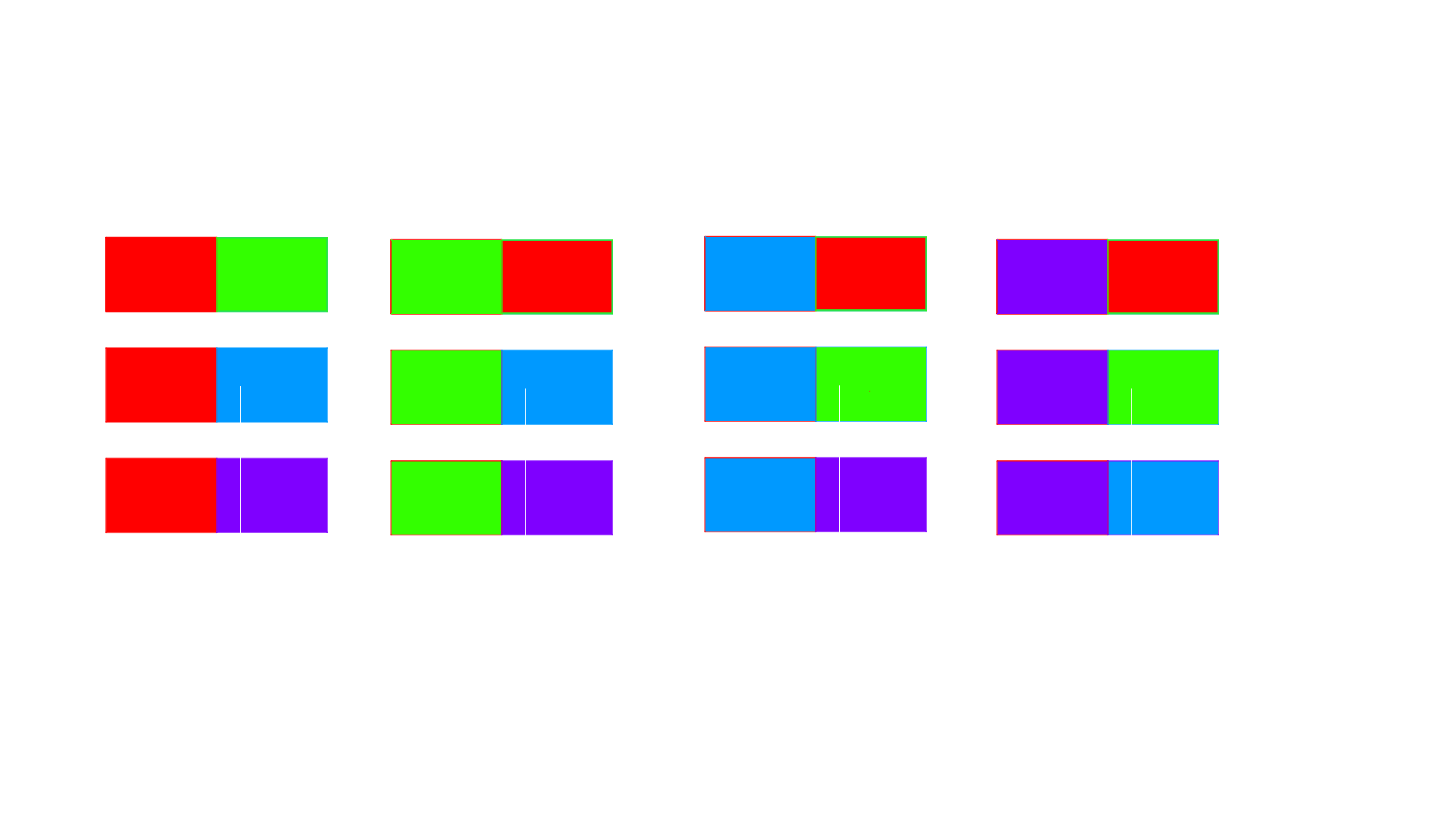
Hay en total $12$ banderas bicolor que se pueden formar con estos $4$ colores. Nota que las banderas bicolores formadas con los colores rojo, verde, azul o morado corresponden a las ordenaciones de $4$ elementos tomadas de $2$ en $2$, que son en total $O_{4}^{2}=12$.
Fíjate que entonces hay $12$ banderas tricolor que terminan en naranja. De manera similar hay $12$ que terminan rojo, $12$ que terminan en verde, $12$ que terminan en azul y $12$ que terminan en morado, es decir doce por cada color.
El número de banderas tricolor es entonces:
$5\cdot 12=5\cdot O_{4}^{2}= O_{5}^{3}=60.$
Observa que $ O_{5}^{3} =5\cdot O_{4}^{2}$, probaremos que esto es válido en general y que $ O_{n+1}^{m+1} =(n+1)\cdot O_{n}^{m}$.
Lema
Sean $n,m\in \mathbb N^+$, $n\geq m$, entonces $O_{n+1}^{m+1}=(n+1)\cdot O_{n}^{m} $.
Demostración
Sean $n,m\in \mathbb N^+$, $n\geq m$ y $A=\set{a_1\dotsc,a_n,a_{n+1}}$ un conjunto con $n+1$ elementos.
$O_{n+1}^{m+1}=\#\set{f:\set{1,\dotsc, m,m+1}\to A=\set{a_1,\dotsc ,a_n,a_{n+1}}\mid f \\\ es\\\ inyectiva}$.
Para cada $i\in \set{1,\dotsc,n+1}$ consideremos el siguiente conjunto:
$B_{i}=\set{ f:\set{1,\dotsc, m,m+1}\to A=\set{a_1,\dotsc ,a_n,a_{n+1}} \mid f \\\ es \\\ inyectiva\\\ y \\\ f(m+1)=a_i }$
en el que estamos considerando, de las funciones que teníamos, sólo aquellas que mandan al último elemento del dominio, $m+1$, en $a_i\in A$.
Demostremos primero que $\#B_i=O_{n}^{m}.$
Notemos que cada una de las funciones en $B_i$ está determinada por los valores que toma en $1,\dotsc, m$, y esto da lugar a una función:
$\begin{pmatrix}1&\dotsc & m\\f(1)&\dotsc & f(m)\end{pmatrix},$
que es una función inyectiva (ya que $f$ es inyectiva) de $\set{1,\dotsc, m}$ en $A\setminus \set{a_i}$ (conjunto que tiene $n$ elementos).
Así, podemos establecer la correspondencia $\phi: B_i\to \set{ g:\set{1,\dotsc, m}\to A\setminus \set{a_i} \mid g \\\ es \\\ inyectiva }$ dada por
$\begin{pmatrix}1&\dotsc & m&m+1\\f(1)&\dotsc & f(m)&a_i\end{pmatrix} \mapsto \begin{pmatrix}1&\dotsc & m\\f(1)&\dotsc & f(m)\end{pmatrix}.$
Se deja al lector verificar que esta correspondencia es biyectiva.
Entonces,
$\#B_i=\# \set{ g:\set{1,\dotsc, m}\to A\setminus \set{a_i}\mid g \\\ es \\\ inyectiva }=O_{n}^{m}$
donde la última igualdad se debe a la notación establecida para el número de ordenaciones.
Observemos ahora que
$B_1\cup \dotsc \cup B_{n+1}= \set{ f:\set{1,\dotsc, m,m+1}\to A=\set{a_1,\dotsc ,a_n,a_{n+1}} \mid f \\\ es \\\ inyectiva}$
donde $B_i\cap B_j=\emptyset$ para toda $i\neq j$, es decir, $ \set{ f:\set{1,\dotsc, m,m+1}\to A=\set{a_1,\dotsc ,a_n,a_{n+1}} \mid f \\\ es \\\ inyectiva}$ es la unión disjunta de $B_1,\dotsc, B_{n+1}$.
Entonces,
$\#(B_1\cup \dotsc \cup B_{n+1})= \# \set{ f:\set{1,\dotsc, m,m+1}\to A=\set{a_1,\dotsc ,a_n,a_{n+1}}\mid f \\\ es \\\ inyectiva}$
y por el principio generalizado de la suma tenemos que:
$\#B_1+ \dotsc + \# B_{n+1}= \# \set{ f:\set{1,\dotsc, m,m+1}\to A=\set{a_1,\dotsc ,a_n,a_{n+1}}\mid f \\\ es \\\ inyectiva}.$
Como $\#B_i=O_{n}^{m}$, para todo $i\in\set{1,\dotsc,n+1}$, entonces
$(n+1)\cdot O_{n}^{m}= \# \set{ f:\set{1,\dotsc, m,m+1}\to A=\set{a_1,\dotsc ,a_n,a_{n+1}} \mid f \\\ es \\\ inyectiva}.$
Por lo tanto
$ O_{n+1}^{m+1} =(n+1)\cdot O_{n}^{m} .$
$\square$
Ejemplo
En la fila de un avión hay tres lugares, ¿de cuántas formas podemos llenarla eligiendo a personas de una familia de seis integrantes?
Notemos que es importante el orden en que coloquemos a las personas y que una persona no puede estar en más de un asiento a la vez por lo que cada forma de acomodar a tres personas de la familia en esos tres lugares, numerados por $1,2$ y $3$, puede ser vista como una ordenación del conjunto $\{1,2,3\}$ en el conjunto formado por los seis integrantes de la familia. Contemos entonces cuántas ordenaciones hay de un conjunto con $6$ elementos tomados de $3$ en $3$.
Sabemos que:
$O_{6}^{3}=6\cdot O_{2}^{5}= 6\cdot5 \cdot O_{4}^{1}.$
Pero si $A=\set{a_1,a_2,a_3,a_4}$ es un conjunto con cuatro elementos, habrá $4$ funciones inyectivas de $\set{1}$ en $A$ y por lo tanto $ O_{4}^{1} =4$. Así:
$O_{6}^{3}=6\cdot5 \cdot 4=120$, y por lo tanto hay $120$ maneras de llenar la fila.
Teorema
Sean $n,m\in \mathbb N^+$, $n\geq m$, entonces $O_{n}^{m}=n(n-1)\dotsc(n-m+1).$
Demostración
Sean $n,m\in \mathbb N^+$, $n\geq m$
Haremos la prueba por inducción sobre $m$
Base de inducción.
Si $m=1$ consideremos $A=\set{a_1,\dotsc,a_n}$ con $n$ elementos. Tenemos que hay $n$ funciones inyectivas de $\set{1}$ en $A$, así:
$O_{n}^{1}=n=n-1+1$ y en este caso se cumple la fórmula.
Paso inductivo.
Supongamos que el resultado se cumple para $m$, es decir que para toda $t\geq m$ $O_{t}^{m}=t(t-1)\dotsc (t-m+1)$ , que es nuestra hipótesis de inducción.
Demostración de que e resultado se cumple para $m+1$ usando la HI.
Sea $n\geq m+1$.
Consideremos $O_{n}^{m+1}= O_{(n-1)+1}^{m+1} $. Por el lema anterior esto es igual a
$ O_{(n-1)+1}^{m+1}=[(n-1)+1] O_{n-1}^{m} .$
Como $n\geq m+1$, tenemos que $n-1\geq m$ y usando la hipótesis de inducción tenemos que
$ O_{n-1}^{m} = (n-1)((n-1)-1)\dotsc ((n-1)-m+1)$
de donde
$ O_{n}^{m+1}=[(n-1)+1] O_{n-1}^{m}= n (n-1)(n-2)\dotsc ((n-1)-m+1).$
Así, $ O_{n}^{m+1}= n(n-1)(n-2)\dotsc (n-m)$, probando con ello que el resultado se cumple para $m+1$.
Por el principio de inducción la fórmula se cumple para toda $m\in \mathbb N^+$.
$\square$
Un caso importante de las ordenaciones se da cuando $n=m$. Recordemos que, de acuerdo a lo que estudiamos acerca de las funciones inyectivas entre conjuntos finitos de la misma cardinalidad, si $A$ es un conjunto finito con $n$ elementos, entonces toda función inyectiva de $\set{1,\dotsc, n}$ en $A$ es también suprayectiva y, por lo tanto, biyectiva.
Definición
Sea $n\in \mathbb N^+$. Dado un conjunto $A=\set{a_1,\dotsc ,a_n}$ con $n$ elementos, las permutaciones de los elementos de $A$ son las funciones biyectivas de $\set{1,\dotsc,n}$ en $A$. Al número de permutaciones de los elementos de un conjunto con $n$ elementos, lo denotaremos por $P_{n}$, es decir, dado $A=\set{a_1,\dotsc ,a_n}$ un conjunto con $n$ elementos
$P_{n}=\#\set{f\mid f:\set{1,\dotsc, n}\to \set{a_1,\dotsc ,a_n}, con\\\ f \\\ biyectiva}.$
Teorema
Sea $n\in \mathbb N^+$, entonces $P_{n}=n(n-1)\dotsc(1).$
Al número $n(n-1)\dotsc(1)$ se le llama el factorial de $n$ y se le denota por $n!$.
Demostración
Sea $n\in \mathbb N^+$. Dado un conjunto $A=\set{a_1,\dotsc ,a_n}$ con $n$ elementos, las permutaciones de los elementos de $A$ son las funciones biyectivas de $\set{1,\dotsc,n}$ en $A$, pero como mencionamos toda función inyectiva de $\set{1,\dotsc, n}$ en $A$ es también suprayectiva y viceversa, por lo que las permutaciones de los elementos de $A$ son las funciones inyectivas de $\set{1,\dotsc,n}$ en $A$, es decir las ordenaciones de $A$ tomadas de $n$ en $n$. Por lo tanto $P_n=O_{n}^{n}$.
De acuerdo al teorema anterior sabemos que $O_{n}^{n}=n(n-1)\dotsc(n-n+1)=n!.$
Así, $P_n=n!$.
Tarea Moral
1. Entre un grupo de siete personas se debe elegir una mesa directiva con un presidente, un secretario, un vocal y un suplente ¿de cuántas maneras se puede elegir esa mesa directiva?
2. En un concurso participan $30$ alumnos y se decidirá quién se lleva cada uno de los tres primeros lugares ¿cuántos posibles resultados se tienen como ganadores del concurso?
3. i) ¿De cuántas maneras pueden posar tres hombres y dos mujeres en línea para una fotografía de grupo?
ii) ¿De cuántas maneras pueden colocarse en línea si una mujer debe estar en cada extremo?
iii) ¿De cuántas maneras las personas del mismo sexo están juntas?
4. ¿De cuántas maneras podemos acomodar once libros en un estante?
Más adelante
En la siguiente nota continuaremos el estudio de las técnicas de conteo, daremos la definición formal de combinaciones, que son el número de subconjuntos de un conjunto dado.
Enlaces relacionados
Enlace a la nota anterior. Nota 21. Conteo, ordenaciones con repetición.
Enlace a la nota siguiente. Nota 23. Combinaciones.
