Introducción
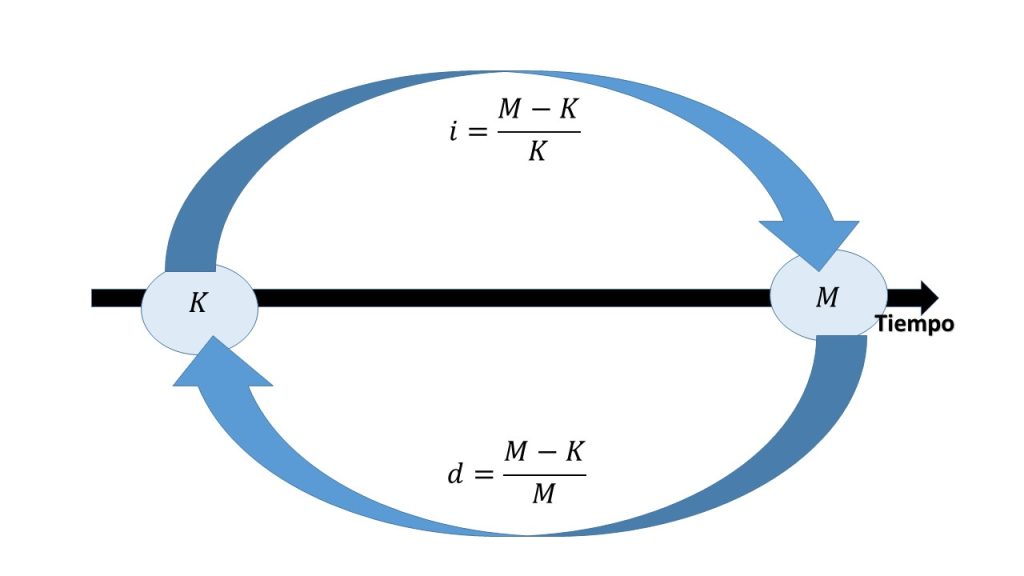
La forma en que se acumula el dinero, tiene dos formas de abordarse, una de ellas es la que se define como tasa efectiva de interés, que tiene que ver con la siguiente expresión: $\frac{(M-K)}{K}.$
y la otra, que considera la proporción de los intereses devengados en relación con el monto, es decir, la tasa de descuento, la cual se denota por: $\frac{(M-K)}{M}.$
De dicha expresión se presenta un nuevo modelo, el de descuento compuesto.
Construcción del modelo de descuento compuesto
En temas anteriores se han abordado fenómenos de acumulación, cuando la tasa de interés incrementa un capital inicial después de haber transcurrido cierto tiempo. De dicho fenómeno se estableció la siguiente expresión:
$$M=K(1+i)^t.$$
Sí suponemos un sólo periodo, la expresión queda: $M=K(1+i).$
Despejando $i$ de dicha expresión, se obtiene: $i=\frac{M-K}{K}.$
En ésa última expresión, nos dice la proporción o el cambio que tendrá un capital, luego de haber transcurrido una unidad de tiempo. En esta sección se construirá un modelo que parte de una tasa o proporción que se aplicará al monto $M$, para obtener el capital invertido $K$, a dicha tasa será llamada tasa efectiva de descuento, misma que será denotada por la letra $d$ y representada por la siguiente expresión:
$$d=\frac{M-K}{M}.$$
Es importante señalar que la tasa de interés, se obtiene como la proporción de los intereses ganados en relación con el capital, mientras que una tasa de descuento parte de la proporción de los intereses en relación al monto.
La siguiente gráfica nos da una representación de éste fenómeno:
Partiendo de la ecuación $d=\frac{M-K}{M}$, se va a construir este nuevo modelo. De esta manera se tiene:
$$dM=M-K$$
$$dM-M=-K$$
$$-dM+M=K$$
$$K=M-dM.$$
Por último factorizando $M$, se obtiene:
$$K=M(1-d)$$
donde:
$K=$Capital inicial
$M=$Monto
$d=$Tasa de descuento
$D=Md=$Descuento total
Ésta nueva expresión permitirá calcular el capital inicial $K$, quitándole una proporción al monto $M$, ésa proporción es la que va a ser determinada por la tasa de descuento $d$. Otro dato importante que es necesario resaltar es el que el descuento obtenido $D$, se resta al monto para obtener el capital, expresado de la siguiente forma:
$$K=M-dM=M-D.$$
Las reglas con las que opera este modelo de tasa de descuento son las mismas que opera el modelo de interés compuesto, sobre todo en lo que se refiere a la temporalidad de las tasas y su relación con los periodos que involucran a la variable $t$.
Para construir el modelo generalizado para $t$ períodos, es necesario usar las siguientes expresiones:
$M=K(1+i)^t$, $M=K(1+i)$, $K=M(1-d).$
Despejando $M$ de la última expresión, se tiene: $M=K(1-d)^{-1}$
Como las expresiones:
$$M=K(1-d)^{-1}=K(1+i)=K(1-d)^{-1}=K(1+i)$$
$$(1-d)^{-1}=(1+i).$$
Luego, se eleva a la potencia $t$ ambos miembros de la igualdad, para obtener:
$(1+i)^t=(1-d)^{-t}.$
Multiplicando por $K$ toda la expresión: $K(1+i)^t=K(1-d)^{-t}=M.$
Donde se obtiene justamente la expresión generalizada que se estaba buscando, la cual es:
$$M=K(1-d)^{-t}.$$
Las reglas que debe cumplir, son las mismas que se establecieron para el modelo de interés compuesto.
Ejercicios resueltos
Ejercicio. Una persona adquirió una deuda hace tiempo, garantizando su pago firmando un pagaré, y el día de hoy desea liquidar. El acreedor le maneja una tasa de descuento por pago anticipado del 8.5% efectivo anual, calcular el valor presente de dicho pagaré, el cual tiene un valor de \$10,000 y cuya fecha de vencimiento es dentro de 9 meses.
Solución
Para encontrar la solución se va a utilizar la siguiente expresión:
$K=M(1-d)^t$
Sustituyendo los datos en la ecuación se tiene:
\begin{align*}
K&=10000(1-.085)^{\frac{9}{12}}\\
&=10000(0.915)^{\frac{9}{12}}\\
&=9355.474526.
\end{align*}
Acumulación y valor presente
Para establecer la relación que hay entre una tasa de interés y una tasa de descuento, se partirá de las siguientes expresiones:
$M=K(1+i)=K(1-d)^{-1}$
dividiendo entre $K$ se tiene: $(1+i)=(1-d)^{-1}$
luego elevando a la potencia $-1$ resulta: $(1-d)=\frac{1}{1+i}$
despejando $d$ se tiene: $d=1-\frac{1}{1+i}$
buscamos un común denominador, con el que se obtiene:
\begin{align*}
d&=\frac{1+i-1}{1+i}\\
&d=\frac{i}{1+i}\\
\end{align*}
Observe que $v=\frac{1}{1+i}$ luego entonces se tiene:
$d=iv.$
Expresión que nos indica que la tasa de descuento es también vista como el valor presente de la tasa de interés.
Ejercicio. Una persona desea invertir $\$100$ a una tasa del $6.5\%$ efectiva anual. Calcular el monto, calcular el valor presente de ésos intereses y comprobar que la tasa resultante es la tasa de descuento.
Solución
Para calcular el monto alcanzado se realiza lo siguiente:
$M=100(1+0.065)=100+6.5=106.5.$
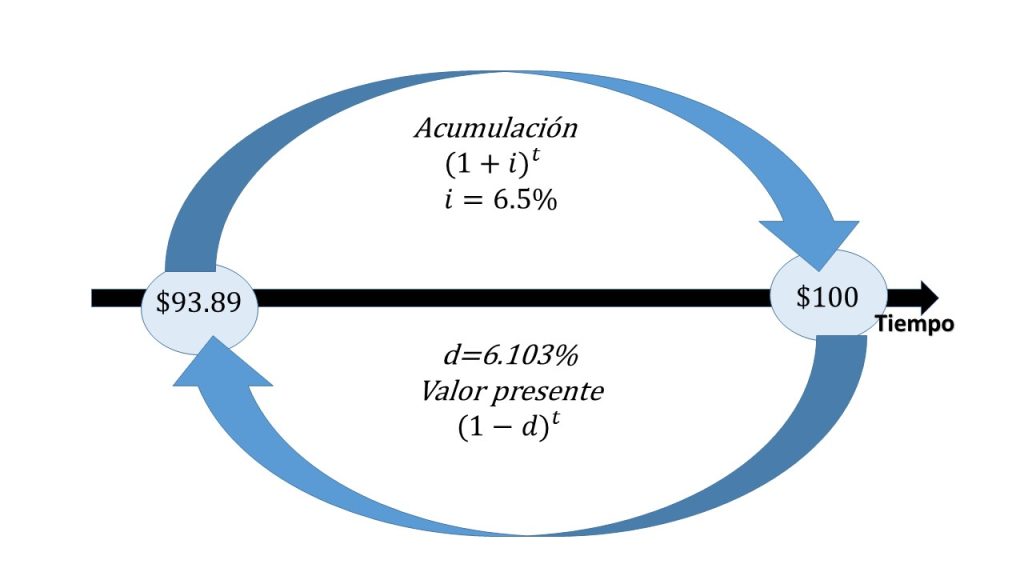
Luego el valor presente del monto calculado $(\$106.5)$, es $\$100$ y el valor presente de los $\$6.5$, calculado a la misma tasa de $6.5\%$ es:
$d=(0.065)\frac{1}{1+0.065}=\frac{0.065}{1.065}=0.06103.$
Por otra parte si a ésos \$100 sea lo que se desea alcanzar tener dentro de un año, y se quiere saber ¿Cuánto es lo que se debe de ahorrar el día de hoy? Para saberlo se hace lo siguiente:
Se utiliza la ecuación: $K(M-d).$
Luego sustituyendo los valores: $K=100(1-0.06103)=100(0.9389671)=\$93.89$
En conclusión ésos \$93.89 es la cantidad que se tiene que ahorrar el día de hoy para obtener \$100 a una tasa del 6.5 de interés anual luego de haber transcurrido un año.
$M=93.89(1+0.65)=\$100.$
Con esto queda comprobado que una tasa de interés efectiva anual del 6.5% es equivalente a una tasa de descuento efectiva anual, del 6.103%.
En la siguiente imagen se muestra el comportamiento de ambos conceptos
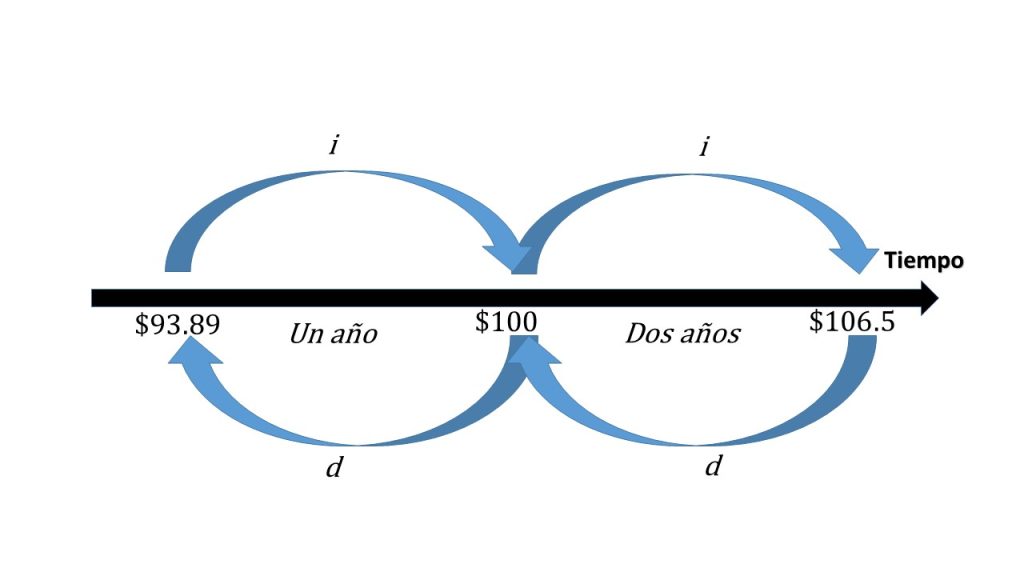
Ejercicio. Usando el mismo ejemplo, calcular para dos años.
Solución
$93.89(1+0.65)^2=\$106.4923$, cantidad que se acumula por dos años.
$106.4923(1-0.06103)^2=93.89$, que resulta ser el capital que se tiene que invertir por dos años con una tasa de descuento.
Gráficamente queda:
Tasas nominales de descuento
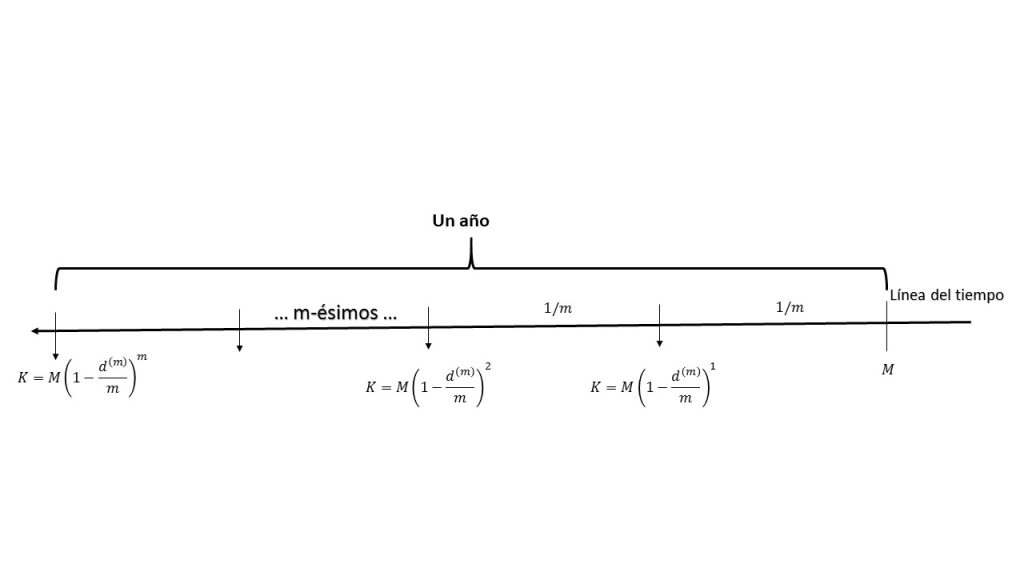
Recordando un poco lo que se ha estado trabajando, una tasa efectiva de descuento por periodo se aplica al monto, luego de haber transcurrido cierto número de periodos $t$, con la finalidad de obtener el capital inicial $K$. Para ésta sección se trabajará con una tasa nominal de descuento denotada por $d^{(m)}$, la cual se caracteriza por ser dividida entre $m$, lo que implica que se descuenta $m$ veces al año, con la misma intención para obtener el capital inicial $K$.
Como se puede apreciar, el comportamiento de las tasas de descuento es análogo al de las tasas nominales de interés, con la diferencia que ésta es descontable $m$ al año. Por lo anterior, se va a estar usando el siguiente modelo:
$$K=M\left(1-\frac{d^{(m)}}{m}\right)^m.$$
En la siguiente gráfica se muestra el comportamiento de ésta expresión.
Es importante señalar que, cuando las tasas nominales de descuento, adquieren los siguientes valores:
$d^{(0)}$= no está definido
$d^{(1)}$= es una tasa de descuento efectiva anual
$d^{(\infty)}$=$\delta$ se trata de una tasa de descuento instantánea
Análogamente aplica lo anterior para las tasas de interés.
La relación que tiene las tasas efectivas de descuento con las tasas nominales de descuento, se describen a través de la siguiente expresión:
$$K=M(1-d)^t=M\left(1-\frac{d^{(m)}}{m}\right)^{mt}.$$
Ejercicios resueltos
Calcule el valor presente de un pagaré con un valor de \$8000 y vencimiento dentro de 3 años 3 meses, entrando en vigencia el día de hoy, con una tasa nominal de descuento pagadera semestralmente del 10%, para el primer año, y del 12% nominal de descuento convertible mensualmente que aplicara para el segundo año, y del 7% nominal de descuento pagadero diariamente para el resto del plazo.
Solución
Se va a hacer uso del modelo:
$$K=M\left(1-\frac{d^{(m)}}{m}\right)^{mt}$$
Para obtener el valor presente se tiene:
\begin{align*}
X&=8000\left(1-\frac{0.07}{365}\right)^{365(1+\frac{3}{12})}\left(1-\frac{0.12}{12}\right)^{(12)(1)}\left(1-\frac{0.1}{2}\right)^{2}\\
X&=8000\left(1-\frac{0.07}{365}\right)^{365+91.25}\left(1-\frac{0.12}{12}\right)^{12}\left(1-\frac{0.1}{2}\right)^{2}\\
&=8000(1-0.000191780082)^{456.25}(1-0.01)^{12}(1-0.05)^{2}\\
&=8000(0.9162111832)(0.8863848717)(0.9025)\\
&=5863.47.\\
\end{align*}
Algunos datos importantes de resaltar son:
Que el primer factor pertenece al último periodo del plazo, ya que siempre es recomendable, comenzar con el periodo más lejano, el cual está dado por una tasa pagadera diaria, lo que implica que está dada por $\frac{0.07}{365}$ y como es efectiva diaria, tiene que ser elevada a la potencia $365+(\frac{3}{12})(365)$, es decir $365+91.25=456.25$ días que corresponde al periodo de 1 año con 3 meses
Dicha cantidad es multiplicada por el segundo factor, en el que se está aplicando una tasa de descuento pagadera mensual del 12%, durante el segundo año, por tal motivo dicho factor se trabajara la tasa denotada por el cociente $\frac{.12}{12}$, para luego ser elevada a la potencia 12, porque es mensual y en un año hay 12 meses.
Por último, el tercer factor está dado por una tasa pagadera semestral, misma que por su naturaleza tendrá que ser dividida entre 2, y elevado dicho factor a la potencia 2, porque un año tiene 2 semestres.
Relación entre las tasas de interés y tasas de descuento
El fenómeno que se ha estudiado, es la forma en que un capital inicial se va transformando con el paso del tiempo a una cierta tasa de interés, de esta forma fue desarrollado el modelo $M=K(1+i)^t$, del cual se desprende el modelo para calcular la tasa de interés: $I=\frac{M-K}{K}.$
Cuando la relación se toma con el monto en vez del capital, se obtiene el concepto de tasa de descuento, el cual es denotado por: $d=\frac{M-K}{M}$, del cual se obtiene el modelo análogo pero con tasa de descuento, el cual es representado por: $M=K(1-d)^{-t}.$
Como se puede observar, los modelos que se han estado usando, parten todos del modelo original, ahora se va a estudiar la relación que existe entre las tasas de interés y las tasas de descuento.
Partiendo de las siguientes expresiones:
$M=K(1+i)^t=K(1-d)^{-t}.$
Ahora representado, pero con tasas nominales:
$M=K\left(1+\frac{i^{(m)}}{m}\right)^{mt}=K\left(1-\frac{d^{(m)}}{m}\right)^{-mt}.$
Por lo expuesto anteriormente, se puede construir la siguiente tabla:

Más adelante…
Se abordarán la aplicación de éstos modelos a otras disciplinas, se mostrará cómo los modelos que se han trabajado, también pueden describir fenómenos naturales, biológicos, demográficos, etc.
Entradas relacionadas
- Ir a Matemáticas Financieras
- Entrada anterior
- Entrada siguiente
