Introducción
Las anualidades anticipadas, se comportan de forma semejante a las anualidades vencidas. Dichas anualidades, tiene su uso principal en el ramo de los seguros, ya que la mayoría de las veces, los pagos que involucran las primas, se realizan de forma anticipada, en pocas palabras, éste tipo de anualidades se usan cuando se requieren al inicio de cada periodo.
Descripción de las anualidades anticipadas
Se utilizan, cuando se desean hacer pagos por adelantado, las reglas para su correcta aplicación son las mismas, que para las anualidades vencidas. Serán denotadas por:
$$\prescript{}{n}{\mathbf{\ddot{A}}}_i=1+v_i^1+v_i^2+…+v_i^{n-2}+v_i^{n-1}$$
$$\prescript{}{n}{\mathbf{\ddot{A}}}_i=\frac{1-v^n}{1-v}.$$
Observación. Las ecuaciones anteriores se pueden escribir como:
$$\prescript{}{n}{\mathbf{\ddot{A}}}_i=1+\prescript{}{n-1}{\mathbf{\ddot{A}}}_i$$
ésta expresión relaciona las anualidades anticipadas con las vencidas, ya que nos muestra como el valor presente de una anualidad vencida de n-1 pagos de un peso, se le suma el peso que debe pagarse en la fecha de valuación, y con esto se logra obtener el valor presente de una anualidad anticipada.
Ahora, si sustituimos el valor de la anualidad que se acaba de mostrar se tiene:
$$\prescript{}{n}{\mathbf{\ddot{A}}}_i=1+\frac{1-v_i^{n-1}}{i}.$$
Generalizando los pagos a una cantidad \$X, la expresión queda:
$$V=X\prescript{}{n}{\mathbf{\ddot{A}}}_i=X(1+\prescript{}{n-1}{\mathbf{\ddot{A}}}_i)$$
$$V=X\left(1+\frac{1-v_i^{n-1}}{i}\right).$$
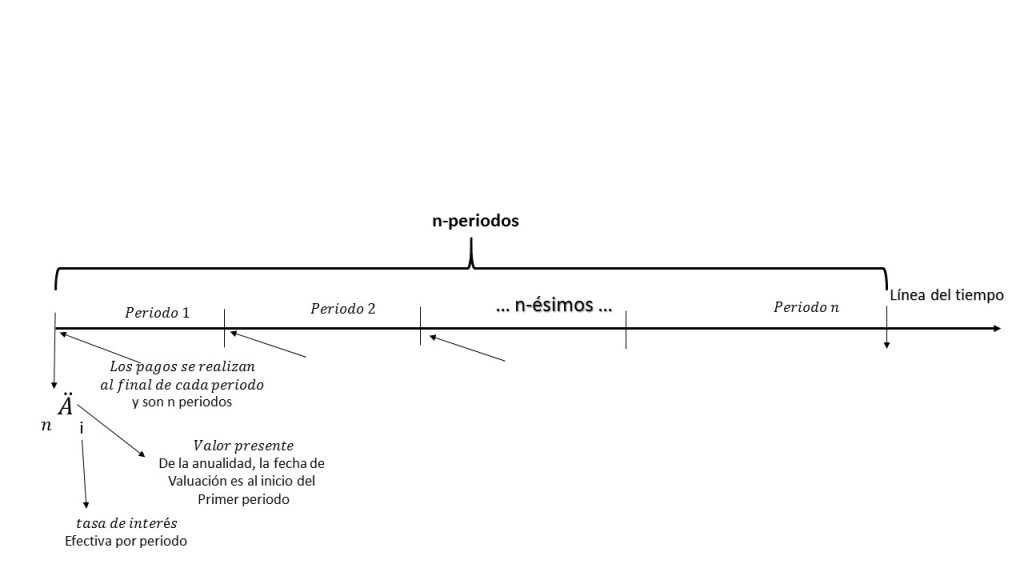
Elaboración propia, basada en Matemáticas Financieras, fundamentos y aplicaciones, Cánovas T. Ed. Trillas, pag. 144.
Ejercicios resueltos
Ejercicio. La gerencia de una plaza de artesanías, quiere ampliar sus locales, y acepta un financiamiento por parte de unos inversionistas con una tasa de interés del 12%, para que los arrendatarios paguen por adelantado, a lo largo de un año. Uno de sus inversionistas decide comprar con un préstamo que le otorgó el banco a una tasa del 8.3%. Se desea saber la cantidad que se debe de pagar al arrendador si la renta de sus locales es de \$14,700?.
Solución
La solución se obtiene calculando primero de la tasa anual, la tasa equivalente efectiva mensual, es decir:
$$(1+0.12)^{\frac{1}{2}}=(1+i)$$
de donde se obtiene el valor de $i=0.9489.$
Cómo las rentas se pagan al inicio de mes, entonces se trata de una anualidad anticipada, por lo que se aplica el siguiente modelo:
$$X=14700\prescript{}{12}{\mathbf{\ddot{A}}}_{0.009489}=14700\left(1+\frac{1-v_{0.009489}^{11}}{0.009489}\right)$$
$$X=14700(10.398566)=152858.92$$
La cantidad que se debe pagar es de: \$152,858.92.
Monto
El monto en una anualidad, es la suma de los pagos periódicos valuados, cada uno, en la fecha que fue realizado el último pago. El proceso para obtenerlo es análogo al que fue usado para obtener el cálculo de las anualidades vencidas, el cual consiste en «traer» todos los pagos a la fecha en la que fue realizado el último.
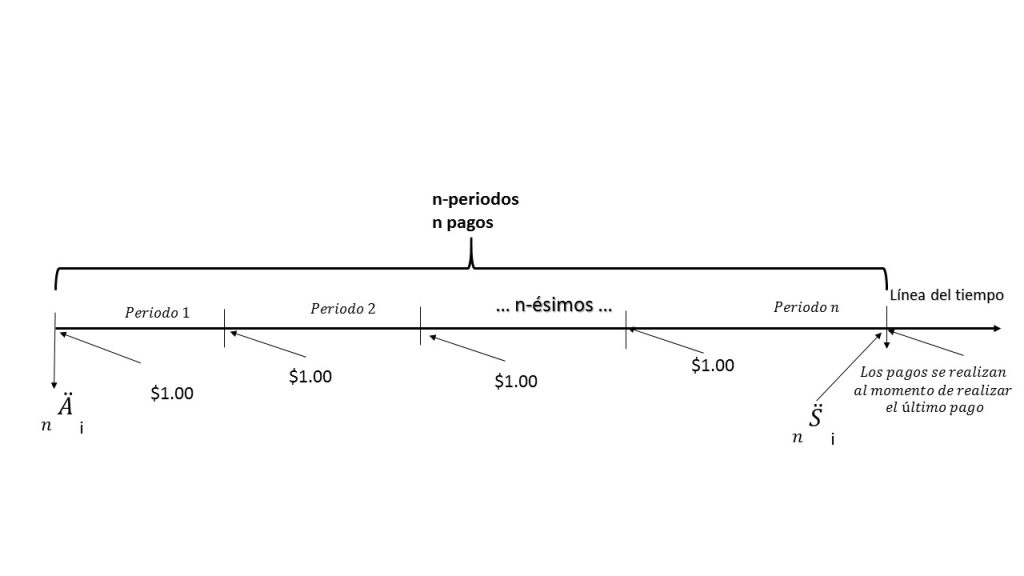
Elaboración propia, basada en Matemáticas Financieras, fundamentos y aplicaciones, Cánovas T. Ed. Trillas, pag. 145.
La fecha de valuación, se toma cuando se realiza el último pago porque no es necesario desarrollar una nueva ecuación, y también porque en la práctica real, difícilmente se encontrará algún caso en donde se tome en cuenta una fecha más allá de la última fecha de pago. De esta forma la expresión queda como sigue:
$$\prescript{}{n}{\mathbf{\ddot{S}}}_i=\prescript{}{n}{\mathbf{S}}_i(1+i)$$
$$\prescript{}{n}{\mathbf{S}}_i=1(1+i)^{n-1}+1(1+i)^{n-2}+1(1+i)^{n-3}+…+1(1+i)^{2}+1(1+i)^{1}+1$$
$$\prescript{}{n}{\mathbf{S}}_i=\frac{(1+i)^n-1}{i}$$
$$M=X.$$
Se llegó a la misma expresión debido a que tomó la fecha del último pago, lo importante. En el caso de la anualidad vencida se hizo al final del periodo, mientras en el de la anticipada se hizo al principio, lo que importa destacar es que la operación que se está realizando, respecto al número de pagos, no es alterada ya que la fecha de valuación es la misma.
Ejercicio. En el mes de mayo de 2022 una empresa depositará cada mes una cantidad de dinero, con el fin de adquirir mercancía para vender en la temporada del buen fin. Situación que llevará a cabo desde el 31 de enero del siguiente año con una duración de 10 meses más. ¿Cuánto deberá ahorrar si las compras que desea hacer, ascienden a un valor de \$35000, considerando que el banco le ofreció una tasa de interés del 7.75% nominal, pagadero mensualmente.
Solución
Tomando en consideración la fecha última en la que realizó su depósito, la cual viene a ser el 30 de noviembre. Luego el número de depósitos que realizará dan un total de 11, y la tasa que se va a utilizar es (0.0775)(12)=0.00645833. Una vez identificados éstos datos, se construye la ecuación de valor la cual nos queda:
$$350,000=\prescript{}{11}{\mathbf{S}}_{0.00645833}$$
de donde:
$$X=\frac{350,000}{\prescript{}{11}{\mathbf{S}}_{0.00645833}}=\frac{350 000}{11.362123}$$
$$X=30 804.10$$
la empresa debe de ahorrar la cantidad de \$30 804.10
Una persona comienza a ahorrar la cantidad de \$300 pesos al inicio de cada mes, y quiere saber, cuál será la cantidad que tendrá ahorrada, luego de haber transcurrido 2 años, si la institución en la que la deja depositada le otorga una tasa de interés del 7% mensual.
Solución
La ecuación que se va a utilizar para resolver el problema es la siguiente:
$$M=X(1+i)\left(\frac{(1+i)^n-1}{i}\right)$$
Sustituyendo los valores que tenemos en la ecuación de valor, la expresión nos queda de la siguiente forma:
$$M=300\prescript{}{24}{\mathbf{\ddot{S}}}_{0.07}$$
$$M=300(1+0.07)\left(\frac{(1+0.07)^{24}-1}{0.07}\right)$$
$$M=300(1.07)\left(\frac{4.072366953}{0.07}\right)$$
$$M=300(1.07)(58.17667076)=18674.7113$$
La cantidad que tendrá ahorrada será de \$18674.71.
Más adelante…
Se continuará trabajando con estos conceptos de anualidades, explorando otros tipos que existen, y no sólo eso, sino que se comenzarán a combinar cada una de ellas, pues nos daremos cuenta que la vida real, tiene una enorme cantidad de variantes para realizar operaciones comerciales, las cuales con el paso del tiempo han surgido como una forma de resolver dichos dilemas, que aparecen a la hora de hacer una operación financiera.
Entradas relacionadas
- Ir a Matemáticas Financieras
- Entrada anterior
- Entrada siguiente
