Introducción

Se tiene hasta este momento, el procedimiento para construir tablas de amortización de muy diversas situaciones, cada una depende de las necesidades que se presenten en las condiciones que se pacte otorgar un crédito que van enfocadas a satisfacer las posibilidades de pago que posea el deudor. Aún con todo lo que se ha visto, falta por revisar el caso donde se otorgan créditos que están sujetos a una tasa de interés variables, esto quiere decir que puede estar cambiando a lo largo de la vigencia o duración del crédito.

Descripción

En éste tema se abordará el tipo de créditos que manejan una tasa de interés variable, lo afecta la cantidad de que se va a pagar en cada periodo, este fenómeno ocurre cuando la institución que otorga el crédito, decide hacer uso de una tasa de referencia como por ejemplo la TIIE. La forma de manejar éste tipo de créditos, es determinar una cierta cantidad la cual va a ser la que será pagada en cada periodo con el fin de saldar o ir liquidando la deuda. Otra alternativa para manejar éstos créditos, es establecer que la forma de pagar la deuda, se haga a través de pagos fijos a la deuda, cada cierto periodo, y que los intereses que genera la deuda se calculen en la fecha que se haga dicho pago.

En cualquier caso, que escojan, las partes involucradas lo que regularmente hacen, es pactar un cierto número de pagos, de acuerdo a la capacidad de pago con la que cuente el deudor, para que sea cubierta la deuda, mientras que la cantidad de intereses que se vaya a pagar, serán calculados sobre la cantidad que falte por pagar del crédito en cada pago. Si por ejemplo la cantidad otorgada en el crédito es de \$86 462, y se quiere pagar en 18 mensualidades y lo que se acaba de mencionar se resume en la siguiente expresión:

$$\frac{86,46}{18}=4803.5$$

Donde cada pago será por la cantidad de \$4803.5, a la cual le falta sumarle la cantidad de intereses que estará determinada según la tasa de referencia que se haya decidido utilizar. También puede darse el caso que la cantidad que se vaya a pagar por concepto de intereses, se haya pactado desde el principio.

Amortización con tasa de interés fija durante toda la vigencia del crédito

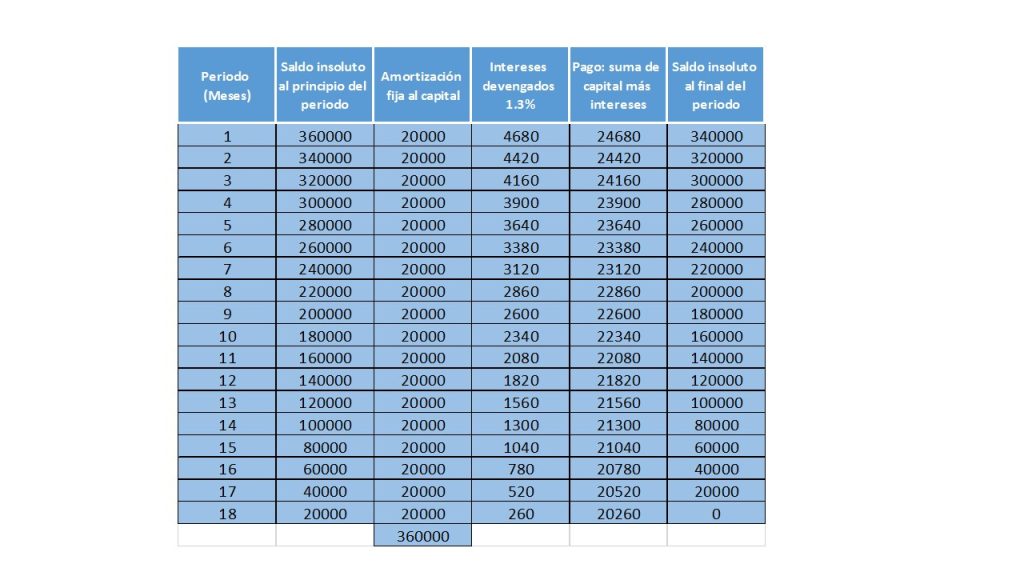
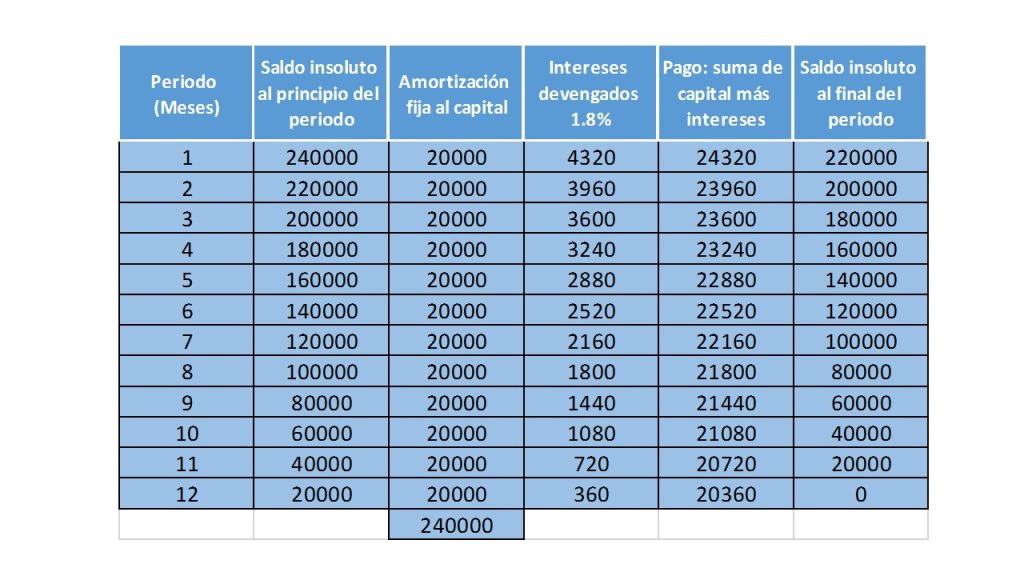
Es tal cual, como lo enuncia su nombre, en este tipo de amortización se da en los créditos que se pacta una tasa fija de interés, esto se puede ver de forma más clara en el siguiente ejemplo: Una empresa solicitó un crédito por una cantidad de \$250,000. La forma en que se planea pagar dicho crédito es mediante pagos mensuales por un año, con una tasa de interés del 1.8% mensual, con pagos fijos directos al capital.

$$\frac{240,000}{12}=20,000.$$

Para construir la tabla de amortización es necesario considerar que los pagos que se van a realizar cada mes, son pagos iguales, pero los intereses se van a ir modificando en cada periodo, esto es a causa de que la cantidad que falte por pagar es sobre la cual se calculan los intereses y éstos irán disminuyendo conforme se vaya liquidando la deuda, esto independientemente de que la tasa de interés permanezca constante.

Para determinar la cantidad que se va a pagar por concepto de intereses, se obtiene multiplicando el saldo insoluto al principio del periodo por la tasa de interés (1.8%).

Y la tabla de amortización queda de la siguiente forma:

Ejercicio. Don Juan desea poner una pastelería en su colonia, para poder hacerlo solicitó un préstamo en el banco ABC, con el que logró que le autorizarán un monto de \$360 mil pesos, el cual quiere pagar con 18 pagos mensuales con una tasa de fija del 1.3% mensual. Construir la tabla de amortización.

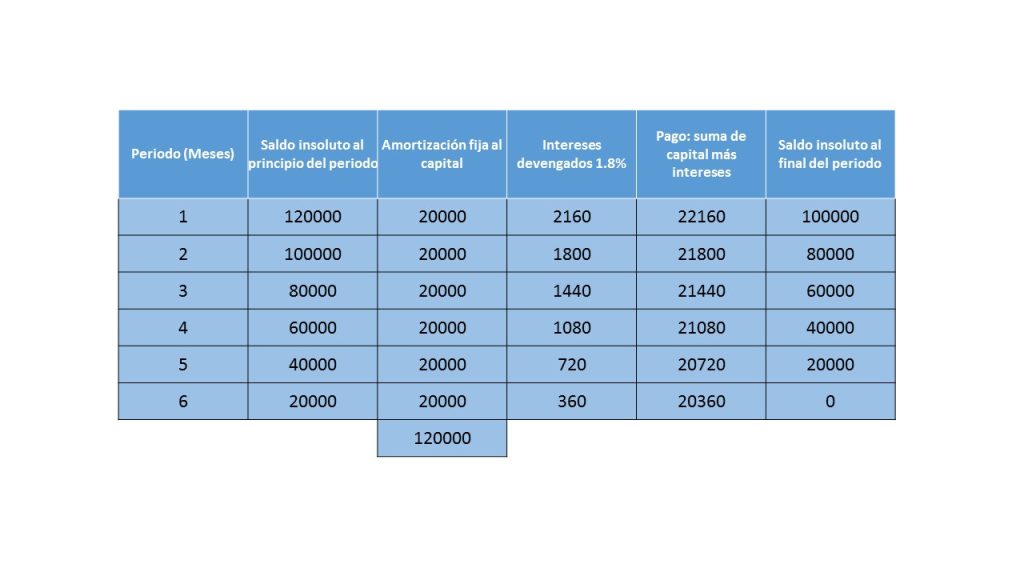
Otro ejemplo, La compañía farmacéutica quiere ampliar su producción, para ellos, le consiguió un crédito por la cantidad de \$120 mil pesos, con pagos semestrales durante 3 años, a una tasa del 1.8% semestral.

Más adelante…

En los siguientes temas se continuará analizando más variantes de las tasas de interés en éste concepto de amortización con la finalidad que se tenga un mejor conocimiento de su comportamiento, sobre todo, para mostrar el tipo de situaciones en que se presentan.

• Ir a Matemáticas Financieras
• Ir a Entrada Anterior
• Ir a Entrada Siguiente