Introducción

Este tipo de fenómenos, ocurre cuando los créditos que se otorgan tienen la característica que su duración es mucho más tiempo, esto se puede interpretar como por ejemplo más de dos años. También ocurre cuando las tasas de referencia que aparecen en los mercados financieros, se comportan de forma inestables, esto quiere decir que tiene variaciones frecuentes, es decir su valor cambia.

Descripción

Cuando ocurre lo anterior y los créditos o préstamos que se hacen utilizando tasas de interés de referencia, se pacta que para dichas operaciones la cantidad de intereses que se vaya a pagar, sea modificada en cada periodo, esto es, la tasa de interés que se va a utilizar será variable de un periodo a otro. Como ya se ha mencionado algunas tasas de referencias son la TIIE, la tasa CETES, etc. Cabe hacer mención que a éstas tasas de interés, al usarlas se le suele añadir uno o dos puntos porcentuales más al momento de utilizarla para obtener la cantidad que se cobrará de interés.

También hay ocasiones en las que se establece que la tasa de interés sea modificada al término de cada año, y así sucesivamente durante toda la vigencia del contrato.

Ahora con respecto a la construcción de las tablas de amortización, en el caso donde se pacta hacer uso de tasas de referencia, implica que la tabla de amortización se tenga que construir en cada periodo, una vez que se conozca el valor de la tasa, es en ése momento que se puede construir.

En el otro caso, lo que se hace es pactar proyecciones a futuro de las tasas, ambas aceptadas por los involucrados.

Fue de los puntos anteriores, la forma de construcción de la tabla de amortización es semejante a como se han venido construyendo.

Veamos el siguiente ejemplo: Una empresa adquiere un crédito por una cantidad de \$175 mil pesos, la cual planean pagar en 10 mensualidades iguales, con cantidad a pagar directo al capital por una suma de \$17,500, con una tasa de interés TIIE mensual considerando 0.3 puntos porcentuales.

Supongamos que el comportamiento de la TIIE serán las siguientes: 0.415%, 0.654%, 0.765%, 0.456%, 0.721%, 0.631%, 0.476%, 0.614%, 0.817%, 0.522%, respectivamente.

La tabla de amortización queda como sigue:

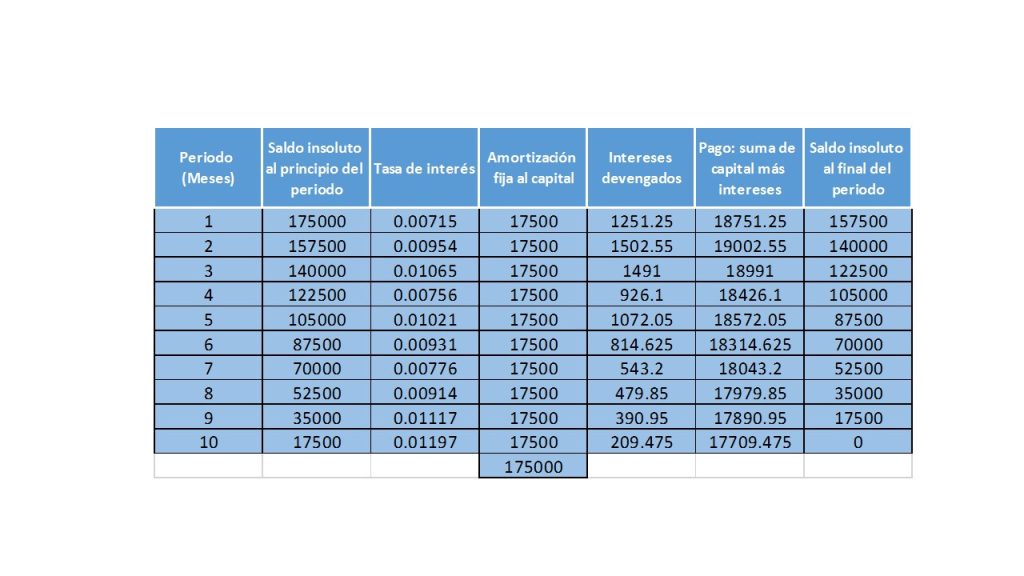
Es pertinente señalar que en la columna con título tasa de interés, aparece la que se había propuesto, más los 3 puntos porcentuales, ya calculados. Los intereses que se van a pagar, tienen que ser calculados en cada uno de los periodos, ya que la tasa de interés varía en cada periodo.

Amortización con tasas de interés variables por periodos

Ocurre en operaciones de crédito que en las que se acuerda entre las partes involucradas, fijar una cierta tasa de interés durante parte de la vigencia del crédito, esto puede ser por ejemplo que los pagos se hagan de forma bimestral y la tasa de interés quede fija sólo por el primer año, mientras que en los años siguientes la puedan modificar, así sucesivamente hasta que termine la vigencia del crédito. Dicho acuerdo de fijar las tasas de interés, puede fijarse desde el inicio de la operación del crédito o irse renegociando cada año, el aspecto que se intenta es considerar circunstancias económicas que prevalezcan en ése momento.

Respecto a la construcción de la tabla de amortización, ésta puede ser construida si se conocen las tasas de interés, esto puede dar, si desde el inicio de operaciones del crédito, quedan fijadas las tasas de interés que serán manejadas durante la vigencia del crédito. Si se fija sólo por el primer año, sólo podrá ser construida para los periodos que estén contenidos en ése año, una vez terminado ese año, se volverá a fijar la tasa que operará en el siguiente y hasta ése momento se podrá elaborar la tabla de amortización.

Otro aspecto a considerar, es que, en este tipo de créditos, pueden usar tasas de referencia o también usar el comportamiento que tuvieron éstas en el año anterior.

Veamos el siguiente ejemplo: Una empresa que se dedica a la serigrafía, planea modernizar todo su inventario en maquinaria y mercancía, para poder hacerlo ha solicitó un crédito por 5 millones de pesos, los cuales piensa pagar en 4 años, con pagos realizados por cuatrimestre, manejando cada año las siguientes tasas, 1.5% para el primer año, 2.4% para el segundo año, 1.9% para el tercer año y 2.3% para el último año.

Para determinar el pago que se realizará en cada periodo se hace lo siguiente:

$$\frac{\$5,000,000}{12}=416,666.667$$

La tabla de amortización correspondiente a éste ejercicio queda de la siguiente forma:

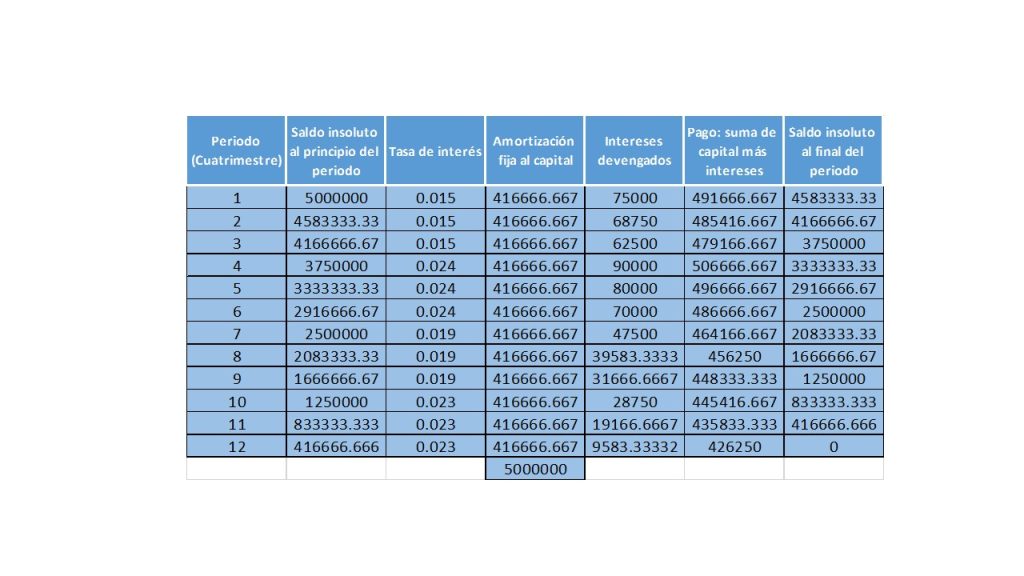
Ejercicios resueltos

Ejercicio. Se tiene un crédito emitido por la cantidad de 3 millones de pesos, con pagos trimestrales iguales, de forma vencida, con una tasa fija del 16.7% para el primer año, 17.8% para el segundo año, 21.7% para el tercer año. Construir toda la tabla.

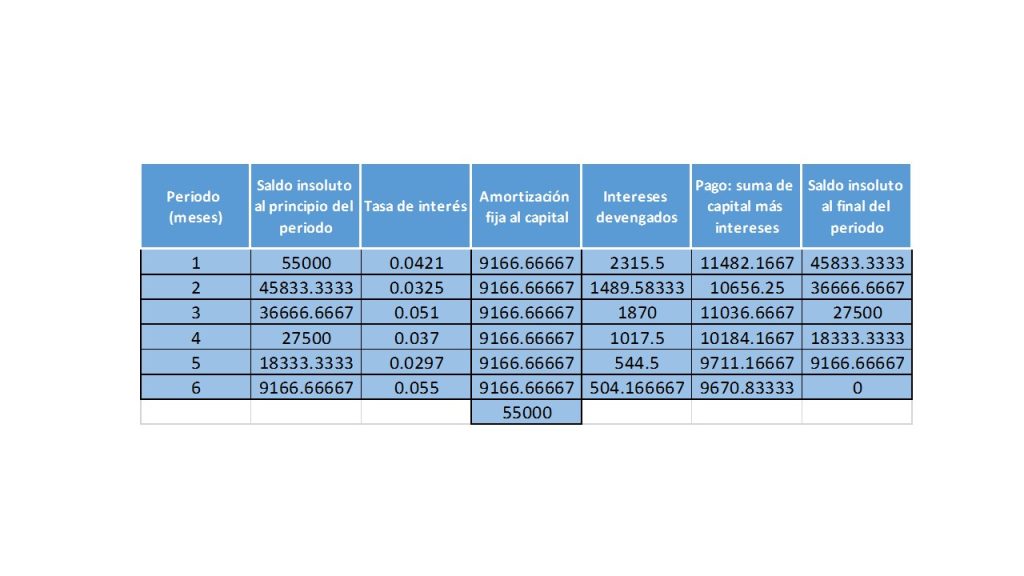
Ejercicio. Se tiene una deuda por la cantidad de \$55000, la cual se tiene considerado pagar en 6 pagos mensuales fijos al capital. Para dicha operación se pactó una tasa de interés de CETE, más dos puntos porcentuales. Supongamos que las tasa CETEs, dan los siguientes resultados: 2.21%, 1.25%, 3.1%, 1,7%, 0.97%, 3.5%, respectivamente para cada pago. Se quiere obtener la tabla de amortización.

Más adelante…

Con éste tema se termina de analizar el concepto de amortización, para que en el siguiente capítulo se aborda la forma en que se pueden hacer valuaciones de valores de renta fija, la forma en que se puede determinar, así como el modo en el que operan.

• Matemáticas Financieras
• Ir a Entrada anterior:
• Ir a Entrada siguiente: Mercado de valores