Introducción

En esta entrada continuaremos estudiando la medida exterior. Veremos maneras alternas de definir la medida exterior y algunos ejemplos importantes.

Más propiedades de la medida exterior.

Podemos tratar de definir una noción análoga de medida exterior reemplazando rectángulos cerrados por rectángulos abiertos. La siguiente proposición nos dice que de hecho coinciden. Esto simplificará considerablemente algunos cálculos más adelante. También ilustra una técnica que usaremos recurrentemente para aproximar una cantidad numerable de elementos: estimamos cada parte con un «error» $\varepsilon$ multiplicado por un término de alguna serie convergente (usualmente $\sum_{k=1}^{\infty} \frac{1}{2^{k}}=1$) de tal manera que el «error total» sea menor o igual a $\varepsilon$ por alguna constante.

Proposición (medida exterior con rectángulos abiertos). La medida exterior se puede calcular usando rectángulos abiertos. Definamos
$$\lambda_0^*(\Omega) = \inf \left\{ \sum_{i\in I} |Q_i| \ : \ \Omega\subseteq \bigcup_{i\in I}Q_i \right\}. $$ Donde $Q_1, Q_2\dots$ son rectángulos ABIERTOS e $I$ es un conjunto de índices a lo más numerable. Entónces $$ \lambda_0^*(\Omega)=\lambda^*(\Omega)$$

Demostración. Para la desigualdad $\geq$, dada una cubierta de $\Omega$ con rectángulos abiertos $\Omega \subseteq \bigcup_{k=1}^{\infty} Q_k$, entonces tomando la cerradura de los rectángulos: $$\Omega \subseteq \bigcup_{k=1}^{\infty} Q_k \subseteq \bigcup_{k=1}^{\infty} \overline{Q_k}.$$ Y
$$ \lambda^*(\Omega)\leq \sum_{k=1}^{\infty} |\overline{Q_k}| = \sum_{k=1}^{\infty} |Q_k|.$$ Tomando ínfimos sobre las cubiertas de rectángulos abiertos se sigue la desigualdad buscada.

Veamos la desigualdad opuesta $\leq$. Si $\lambda^*(\Omega)=\infty$, por lo anterior $\lambda_0^*(\Omega)\geq \lambda^*(\Omega) =\infty$, por tanto $\lambda_0^*(\Omega)=\infty$ y se da la igualdad. Así que basta suponer que $\lambda^*(\Omega)<\infty$.

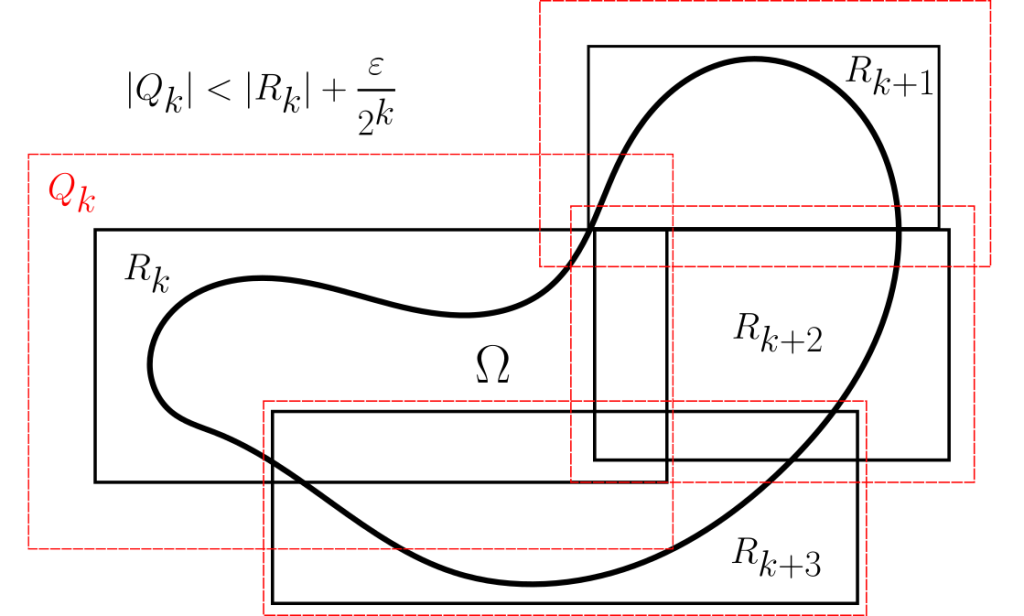
Sea $\varepsilon>0$ arbitrario. Al ser $\lambda^*(\Omega)$ ínfimo (finito), podemos tomar una cubierta de rectángulos cerrados $\Omega\subseteq \bigcup_{k=1}^{\infty}R_k$ tal que $$\sum_{k=1}^{\infty} |R_k| < \lambda^*(\Omega) + \varepsilon \leq \sum_{k=1}^{\infty} |R_k| +\varepsilon.$$ Por la aproximación con rectángulos abiertos, para cada $k=1,2,\dots$, podemos encontrar un rectángulo abierto $Q_k$ tal que $R_k\subseteq Q_k$ y $|Q_k|<|R_k|+\frac{\varepsilon}{2^{k}}$. Entonces $\Omega\subseteq \bigcup_{k=1}^{\infty}R_k \subseteq \bigcup_{k=1}^{\infty}Q_k$. Luego: $$\lambda_0^*(\Omega)\leq \sum_{k=1}^{\infty} |Q_k|<\sum_{k=1}^{\infty}(|R_k|+\frac{\varepsilon}{2^{k}})< \lambda^*(\Omega) + 2 \varepsilon.$$ Como lo anterior es cierto para cualquier $\varepsilon>0$ se sigue que $\lambda^*(\Omega) \geq \lambda_0^*(\Omega)$.

$\square$

Como ya lo habíamos mencionado, la medida exterior de los rectángulos coincide con su volumen.

Proposición. La medida exterior de un rectángulo (abierto o cerrado) $R$ coincide con su volumen: $$\lambda^*(R)=|R|.$$

Demostración. Veamos primero el caso en el que $R=[a_1,b_1]\times [a_2,b_2]\times \dots \times [a_n,b_n]$ es cerrado. Al considerar la cubierta de $R$ con el propio $R$, se sigue de inmediato que $$0\leq \lambda^*(R)\leq |R|.$$

Veamos la desigualdad opuesta. El caso en el que $R$ es degenerado es trivial, así que supongamos que $R$ no es degenerado. La idea es usar la equivalencia de la medida exterior con rectángulos abiertos y la compacidad de $R$.

Sea $Q_1,Q_2,\dots$ cualquier cubierta de rectángulos abiertos de $R$. Supongamos sin pérdida de generalidad que la cubierta es numerable (si la cubierta es finita, el argumento debajo aplica de igual manera): $R\subseteq \bigcup_{k=1}^{\infty} Q_k$. Como $K$ es compacto, podemos extraer alguna subcubierta finita, digamos $$R\subseteq \bigcup_{k=1}^{N} Q_k.$$ Al ser una cubierta finita, se sigue de las propiedades del volumen de rectángulos que: $$|R|\leq \sum_{k=1}^{N}|Q_k| \leq \sum_{k=1}^{\infty}|Q_k|.$$ Como lo anterior es cierto para cualquier cubierta con rectángulos abiertos, al tomar ínfimos se sigue que $$|R|\leq \lambda_0^*(R)=\lambda^*(R).$$

Si $R$ es un rectángulo abierto, la cubierta de $R$ con el propio $R$ (o su cerradura) establecen $\lambda^*(R)\leq |R|$. Para la otra desigualdad podemos usar la aproximación por rectángulos cerrados, la monotonía de la medida exterior y el caso anterior: $$|R|=\sup_{\substack{Q\subseteq R; \ Q \text{ cdo.}}} \{|Q| \}=\sup_{\substack{Q\subseteq R; \ Q \text{ cdo.}}} \{ \lambda^*(Q) \} \leq \lambda^*(R).$$

$\square$

Ejemplo. Si $A\subseteq \mathbb{R}^n$ es acotado, entonces $\lambda^*(A)$ es finita pues podemos encontrar un rectángulo $R$ suficientemente grande tal que $A\subseteq R$ de modo que $\lambda^*(A)\leq \lambda^*(R)=|R|<\infty$.

$\triangle$

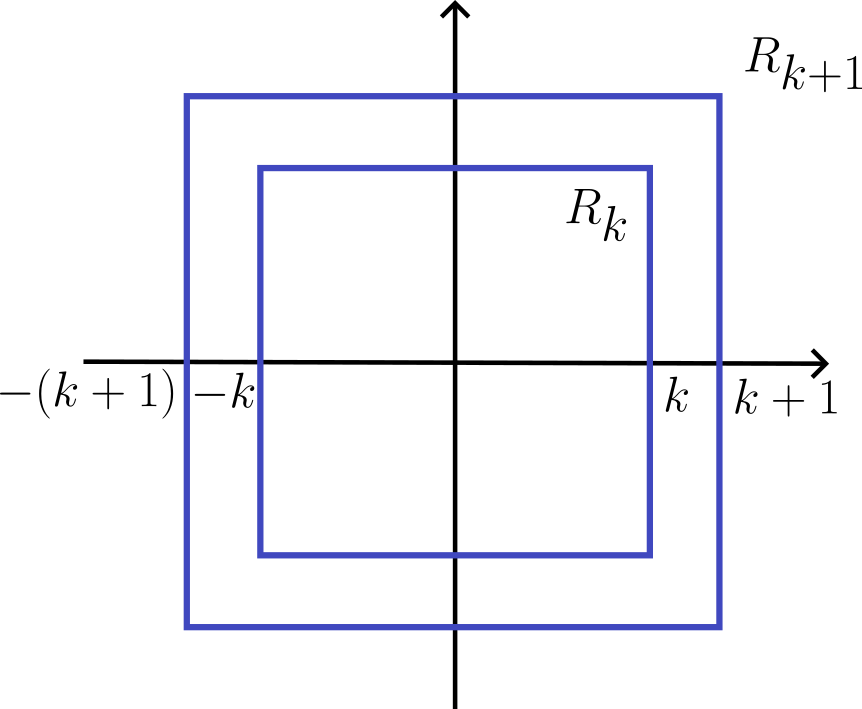
Ejemplo. La medida exterior de $\mathbb{R}^n$ es $\infty$.

Consideremos le sucesión de rectángulos anidados $R_k=[-k,k]\times [-k,k]\times \dots \times [-k,k]$ $k=1,2,\dots$. Luego $\lambda^*(R_k)=|R_k|=(2k)^n$. Como $R_k\subseteq \mathbb{R}^n$ $\forall$ k, entonces $(2k)^n\leq \lambda^*(\mathbb{R}^n)$ $\forall k$ así que necesariamente $\lambda^*(\mathbb{R}^n)=\infty$.

$\triangle$

Más adelante…

Seguiremos con nuestro estudio de la medida exterior. Nos enfocaremos en estudiar las propiedades relacionadas con la «aditividad» de la medida exterior, aunque veremos un ejemplo clásico de que ésta en general no es aditiva.

Tarea moral

• Usando que todo conjunto numerable tiene medida exterior cero, prueba que $\mathbb{R}^n$ NO es numerable.
• Demuestra que la medida exterior de un polígono especial coincide con su volumen.
• Demuestra que la medida exterior también se puede calcular mediante polígonos especiales. Es decir, $$\lambda^*(\Omega) = \inf \left\{ \sum_{i\in I} |P_i| \ : \ \Omega\subseteq \bigcup_{i\in I}P_i \right\}. $$ Donde $P_1, P_2\dots$ son polígonos especiales e $I$ es un conjunto de índices a lo más numerable.