Introducción

Veamos un último ejemplo de los problemas que podremos resolver con la teoría que desarrollaremos más adelante. Se conoce como el problema de la ruta más corta, y la idea es muy sencilla. Se tiene una red de localizaciones en un mapa. Hay algunos tramos que conectan localizaciones. Atravesar cada uno de ellos tiene cierto costo (asociado por ejemplo, con la distancia). Si nos dan un origen y un destino, ¿cómo podremos determinar el camino a seguir que nos lleve del origen al destino con el menor costo posible? Comencemos con un ejemplo concreto.

Ejemplo del problema de la ruta más corta

Supongamos que un empleado sale de trabajar a cierta hora de la noche y para regresar a su casa evalúa las posibles rutas a tomar en una aplicación móvil. La aplicación le indica algunas calles y avenidas que lo llevan de su trabajo (1) a su casa (7). Los vértices de en medio (2, 3, 4, 5 y 6) representan los cruces de calles por los que se transita en estas posibles rutas. También le indica cual es el tiempo que le tomará ir por cada calle o avenida en minutos, tomando en cuenta no solo la distancia, sino también el tráfico y los accidentes que se presentan. El empleado busca la ruta más rápida para poder llegar a su casa a descansar.

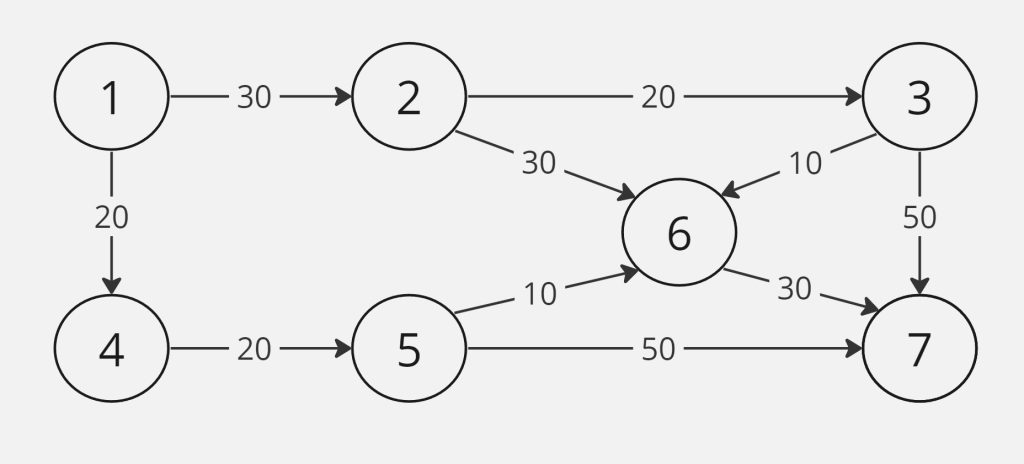
Aunque parezca que este problema es muy geométrico, en realidad también se puede plantear en términos algebraicos, como veremos a continuación.

Variables de decisión del problema de la ruta más corta

En otros problemas hemos tenido variables de decisión que nos dicen cuánto producir, cuánto transportar, cuánto comer, etc. En esta caso, nuestras variables de decisión no representarán una cantidad, sino simplemente una decisión de «sí» o «no». Lo que haremos es establecer una variable $x_{ij}$ por cada uno de los posibles tramos del destino $i$ al $j$, y será una variable binaria que indique la decisión de recorrer o no tal tramo. Si sí lo recorremos tendrá valor $1$ y si no, tendrá valor $0$.

Por ejemplo si tomamos la ruta {1,2,3,7}, tendremos $x_{12} = x_{23} = x_{37}=1$, lo cual nos indicará que sí se recorren los tramos $(1,2)$, $(2,3)$, y $(3,7)$. Por otro lado, tomaremos $x_{ij} = 0$ para los demás tramos, que nos indicará que no se recorren.

Explícitamente, en nuestro ejemplo tomaremos variables $x_{ij}$ con $i<j$, y tales que $(i,j)$ esté en el conjunto $A$ de todas las parejas $i<j$ para las cuales haya un tramo entre $i$ y $j$ (en cualquier dirección). La interpretación que les daremos será la siguiente:

$$x_{ij}=\begin{cases} 1 \quad \text{si se recorre el tramo $(i,j)$} \\ 0 \quad \text{si no}. \end{cases}$$

Restricciones del problema de la ruta más corta

Ya establecidas las variables de decisión, lo que debemos hacer ahora es dar restricciones que hagan que los tramos elegidos definan una ruta.

Pensemos en qué sucede desde el trabajo. De ahí es donde debemos empezar. Solamente debemos tomar un tramo desde el trabajo, pues si pasamos por el trabajo más de una vez, en realidad nos podemos ahorrar esa vuelta que dimos de más para llegar más rápido a casa . Esto significa o que $x_{12} = 1$, o que $x_{14}=1$, y sólo una de estas dos igualdades se cumple. Ya que las variables sólo serán $0$ ó $1$, otra manera de escribir esto mismo es pedir que $$x_{12}+x_{14}=1.$$

Del mismo modo, debemos garantizar que se llegue a casa por un solo tramo, que se puede escribir como $$x_{37}+x_{57}+x_{67}=1,$$ o bien $$-x_{37}-x_{57}-x_{67}=-1.$$

Para el resto de las zonas, debemos tomar en cuenta que si se entra a una, también se debe salir. Y si no se entra tampoco se sale. Veamos qué pasa, por ejemplo, con el cruce 2:

• Si se entra entonces $x_{12}=1$. Deberá cumplirse entonces que $x_{23} = 1$ o $x_{26} = 1$ y sólo una de éstas.
• Si no se entra entonces $x_{12}=0$. Deberá cumplirse entonces: $x_{23}=x_{26} = 0$.

Podemos reescribir ambos casos anteriores de manera simplificada con la igualdad $$x_{12} = x_{23}+x_{26},$$ que también se puede escribir como $$x_{23}+x_{26}-x_{12}=0.$$

Cada uno de los cruces $3,4,5,6$ nos dan restricciones similares.

Función objetivo del problema de la ruta más corta

Finalmente, debemos determinar cuánto nos costará recorrer una ruta una vez fijas las variables de decisión. Esto es sencillo. Si el tramo de $i$ a $j$ tiene un costo de $c_{ij}$, entonces recorrerlo nos costará $x_{ij}c_{ij}$. En nuestro problema, la función objetivo quedaría como sigue:

\begin{align*}z&=30x_{12}+20x_{14}+20x_{23}+8x_{26}\\
&+10x_{36}+50x_{37}+20x_{45}+10x_{56}\\
&+50x_{57}+30x_{67}.\end{align*}

Resumen de formulación del problema de la ruta más corta

Así, el problema de ruta más corta que vimos como ejemplo queda descrito como sigue.
\begin{align*}
z&=30x_{12}+20x_{14}+20x_{23}+8x_{26}\\
&+10x_{36}+50x_{37}+20x_{45}+10x_{56}\\
&+50x_{57}+30x_{67}.
\end{align*}
\begin{align*}
s.a.\\
x_{12}+x_{14} &= 1\\
-x_{12}+x_{23}+x_{26} &= 0\\
-x_{14}+x_{45} &= 0\\
-x_{23}+x_{36}+x_{37} &= 0\\
-x_{45}+x_{56}+x_{57} &= 0\\
-x_{26}-x_{36}-x_{56}+x_{67} &= 0\\
-x_{37}-x_{57}-x_{67} &= -1\\
x_{ij}=0,1 \quad \forall (i,j) &\in A.\\
\end{align*}

Este problema podría plantearse en general, bajo algunas condiciones sobre el tipo de mapas en los que se puede resolver. Este es un modelo lineal entero binario que tiene la propiedad de que puede ser resuelto eficientemente con algoritmos de programación lineal

Otro ejemplo de ruta más corta

La idea anterior puede servir no sólo para resolver problemas en donde nos interesen las distancias geográficas. En otros problemas, nos interesa llegar «rápidamente» a una meta que tenemos, pero quizás con una noción un poco distinta de «rapidez». Esto puede querer decir llegar a un objetivo de negocio en pocos días. Hay casos en los que también podremos plantear esta situación como un problema de ruta más corta. Considera el siguiente ejemplo.

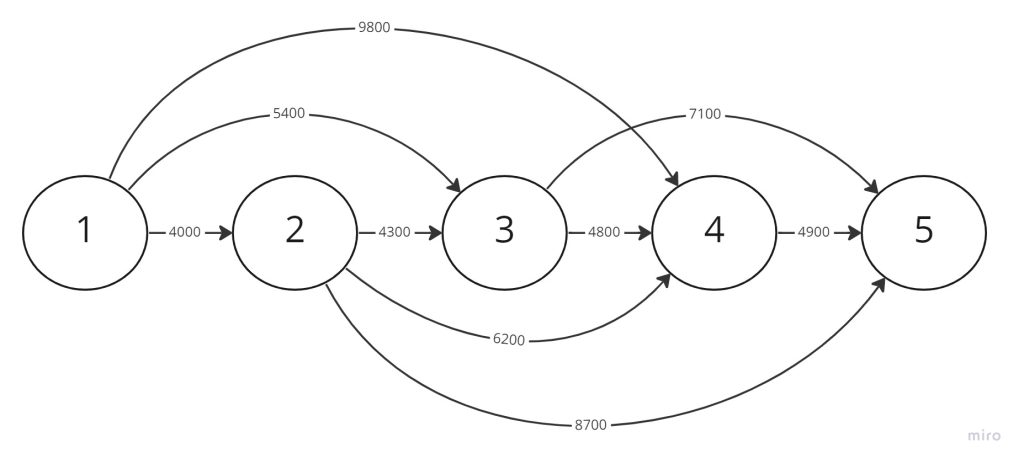
Una compañía que renta automóviles está desarrollando una política de reemplazo para su flotilla de automóviles en un horizonte de planeación de 4 años. Al inicio de cada año, un automóvil se reemplaza o se conserva en operación durante un año más. Un automóvil debe estar en servicio de 1 a 3 años. La siguiente tabla proporciona el costo de reemplazo como una función del año en que se adquiere un automóvil y los años en operación.

Equipo adquirido al inicio del año	Costo de reemplazo ($) para años dados en operación
	1	2	3
1	4000	5400	9800
2	4300	6200	8700
3	4800	7100	______
4	4900	______	______

El problema puede formularse como una red en la que los nodos 1 a 5 representan el inicio de los años 1 a 5. Los arcos a partir del nodo 1 (año 1) pueden llegar a los nodos 2, 3 y 4 porque un automóvil puede estar en operación de 1 a 3 años. Los arcos a partir de los demás nodos pueden interpretarse del mismo modo. La longitud de cada arco es igual al costo de reemplazo. La solución del problema es equivalente a determinar la ruta más corta entre los nodos 1 y 5.

El problema puede ser representado con la siguiente red:

Más adelante…

Con esto terminamos los últimos planteamientos de problemas ejemplo de programación lineal. Por un lado, estos nos servirán como motivación para saber el tipo de problemas que podemos resolver. Por otro lado, nos irán guíando para el desarrollo de distintas técnicas de solución.

Ya que conocemos el tipo de problemas que podremos resolver, platicaremos ahora un poco de la teoría general que respaldará nuestros métodos. En la siguiente entrada introduciremos algunos aspectos teóricos de los problemas de programación lineal.

Tarea moral

1. Intenta resolver el ejemplo de la ruta más corta que pusimos como ejemplo usando técnicas elementales y una división en casos. ¿Cuál sería la ruta más corta? ¿Por qué crees que sea importante tener métodos generales si este ejemplo se puede resolver de manera muy sencilla con unos pocos casos?
2. Formula el segundo ejemplo del problema de la ruta más corta como un problema de programación lineal. ¿Qué interpretación tendría encontrar la ruta más corta?
3. Pedro va en auto diariamente a la facultad. Pedro siempre toma la misma ruta para llegar a la facultad. Por desgracia, en ocasiones hay algunos asaltos sobre la ruta, y a Pedro le gustaría disminuir lo más posible la probabilidad de que esto suceda. Pedro ha decidido por lo tanto elegir una ruta que minimice la probabilidad de ser asaltado.
   La red presentada a continuación muestra las posibles rutas de su casa a la facultad y la probabilidad asociada de no ser asaltado en cada segmento.

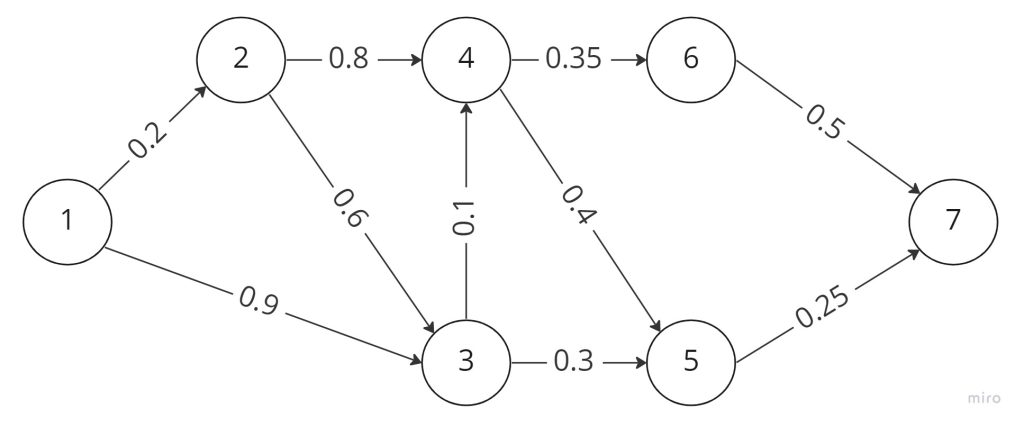
La probabilidad de no ser asaltado en la ruta es el producto de las probabilidades de sus segmentos. Por ejemplo, la probabilidad de no ser asaltado en la ruta $1 \rightarrow 3 \rightarrow 5\rightarrow 7$ es $.9 \times .3 \times .25 = .0675$. El objetivo de Pedro es seleccionar la ruta que minimice la probabilidad de ser asaltado.
¿Puedes pensar en una manera de formular este problema como un modelo de la ruta más corta? Como sugerencia, trata de usar la función logaritmo.

4. Una vez planteado el problema anterior, intenta resolverlo con herramientas básicas y algunos casos.
5. Intenta plantear por tu cuenta una versión general del segundo problema que vimos en esta entrada. ¿Qué sucedería si tenemos más periodos en los que se puede renovar la flotilla? ¿Cómo se vería el problema?

Entradas relacionadas

• Ir a Investigación de Operaciones
• Entrada anterior del curso: El problema de producción e inventario
• Entrada siguiente del curso: Forma canónica y forma estándar de un problema lineal